含未知輸入的離散線性系統新型遞歸濾波方法
花玉,王娜,b,趙克友
(青島大學 a. 自動化學院;b. 山東省工業控制技術重點實驗室, 山東 青島 266071)
0 引言
當系統存在過程噪聲和測量噪聲的情況下,傳統卡爾曼濾波器[1]能遞歸估計線性系統狀態,但是其要求干擾噪聲必須是高斯白噪聲。因為系統的不確定干擾可能不是白噪聲,且某些輸入無法測量,因此卡爾曼濾波器的效果有時并不理想。
在系統分析中,未知輸入可以表示無法測量的干擾、未建模動態、系統故障等。因此,研究含有未知輸入的系統估計問題具有極大意義。這類問題的解決方案在控制系統設計中的干擾抑制[2-3]、故障檢測[4]、電池狀態估計[5]等許多實際應用中發揮重要作用。
近年來,存在未知輸入的濾波器設計問題引起了相當大的關注。根據系統不同,該問題可大致分為兩類:帶有直通項的濾波器設計[6-12]和不帶直通項的濾波器設計[13-17],其中關于不帶直通項的濾波器設計文獻相對較少,具有進一步研究的價值。
最初,解決這類問題的方法是系統狀態擴維,將未知輸入向量作為系統狀態的附加部分,然后對擴維系統應用卡爾曼濾波器。這種方法通常將未知輸入假定為常值偏差或某些具有已知統計特性的隨機過程[18],但這些假設在實際應用中可能是無效的。因此,許多研究開始轉向存在任意未知輸入情況下的系統狀態估計問題。解決此類問題的方法通常是通過解耦來實現狀態估計。
自從KITANIDIS P K開展工作以來,對未知輸入估計問題的研究開始轉向最優濾波器,其為不帶直通項的線性系統,開發了一種最小方差無偏(minimum variance unbiased, MVU)的最優濾波器[13]。該濾波器通過在無偏條件的約束下將狀態協方差矩陣的跡最小化以獲得狀態估計。該濾波器被文獻[14]進一步擴展為一類參數化解決方案。上述文獻雖然解決了存在未知輸入時的狀態估計問題,但沒有給出未知輸入的估計值。對一些實際問題來說,未知輸入的估計值同樣重要。文獻[16]提出一種魯棒兩段卡爾曼濾波器(robust two-stage kalman filter,RTSKF),首先識別初始時刻未知輸入的動態模型,然后用識別的模型對未知輸入和狀態進行估計,其能夠給出未知輸入的具體估計值,但沒有證明所得結果最優。文獻[17]提出一種三步迭代濾波器(recursive three-step filter, RTSF),能夠同時獲得系統狀態和未知輸入的最小方差無偏估計,并證明了未知輸入估計值最優。盡管上述濾波器可以解決存在未知輸入下系統狀態及未知輸入的估計問題,但都有一個前提條件:系統狀態方程中未知輸入的系數矩陣列滿秩。
本文基于RTSF思路,提出一種新型三步迭代濾波器(novel recursive three-step filter,NRTSF),在系統狀態方程受未知輸入影響時估計系統狀態和未知輸入,該濾波器不需要系統方程中未知輸入系數矩陣列滿秩,其應用條件比上述濾波器寬松。
1 問題描述
考慮如下帶有未知輸入的隨機線性離散時變系統:
xk=Ak-1xk-1+Gk-1dk-1+wk-1
(1)
yk=Ckxk+vk
(2)
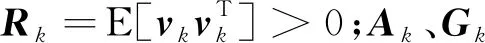
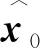
2 NRTSF設計
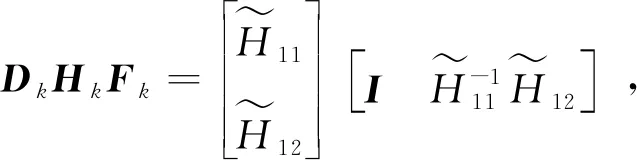
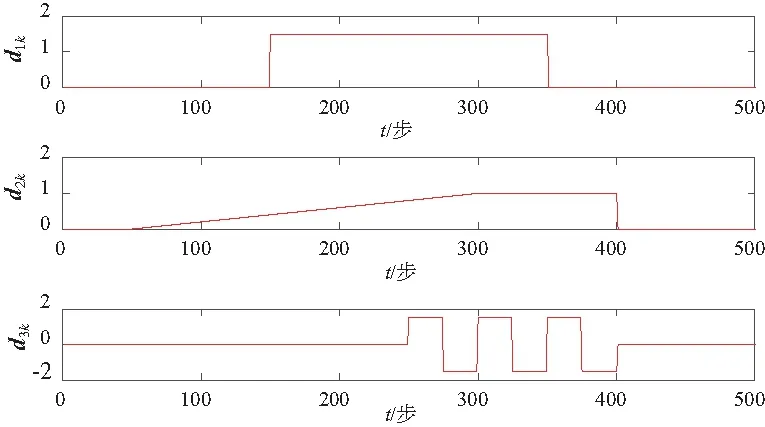
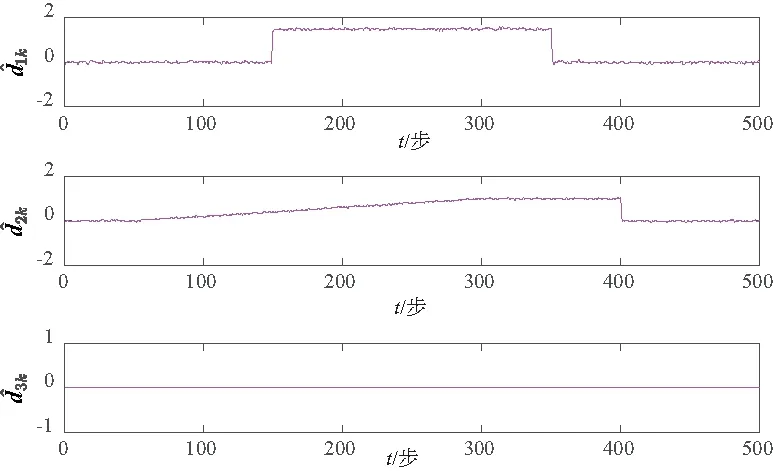
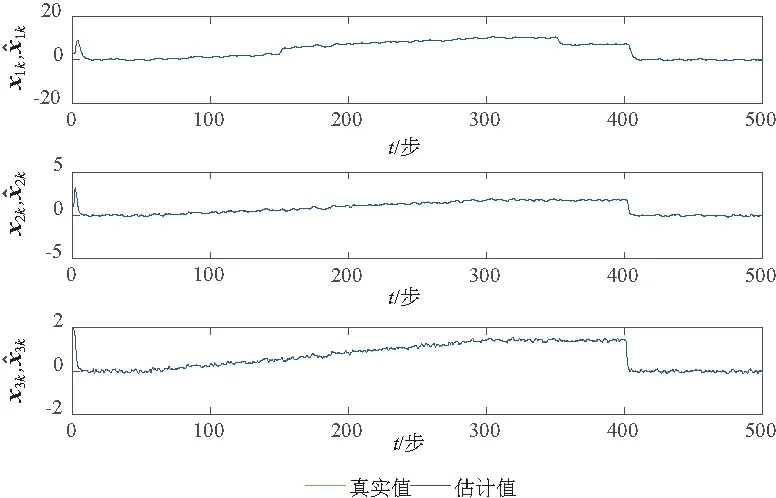
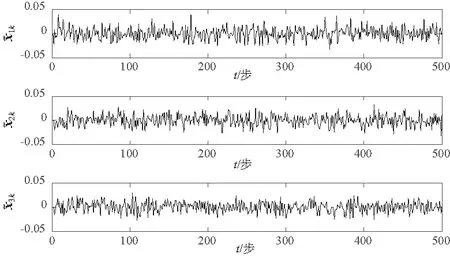
GILLIJNS S在文獻[17]中提出的經典RTSF可以解決上述系統的狀態估計問題,但是使用RTSF的前提條件是系統方程中未知輸入的系數矩陣Gk-1必須滿足rank(Gk-1)=m,k=1,2,…。針對系統方程中未知輸入系數矩陣不滿秩的情況,即rank(Gk-1)=rk 假如rank(Gk-1)=rk≤m,對其進行如下滿秩矩陣分解: (3) 換言之,存在非奇異陣Dk∈Rp×p和Fk∈Rm×m,使 (4) 則原系統方程式(1)改寫為 (5) 基于新的系統狀態方程式(5)和測量方程式(2)設計NRTSF如下: (6) (7) (8) 1)虛擬未知輸入的無偏估計 (9) 其中 (10) 證明: 該證明與文獻[17]中定理1的證明相似,因此省略。 由于對應于式(9)的最小二乘解滿足定理1,因此這個最小二乘解無偏。但根據Gauss-Markov定理,它不一定是最小方差解,因為在一般情況下 其中c表示正實數。 2)虛擬未知輸入的MVU估計 證明: 該證明與文獻[17]中定理2的證明相似,因此省略。 (11) (12) (13) (14) 證明:使用拉格朗日乘子法來證明此定理。令拉格朗日式 (15) (16) 式(16)和式(12)組成線性系統方程組 (17) 將式(14)代入式(8)產生等效狀態更新: 將式(14)代入式(13)可得 將NRTSF總結如下: 1)時間更新 2)虛擬未知輸入估計 3)測量更新 為了驗證本文提出的NRTSF有效性,本節采用與杜濤[19]一致的示例進行仿真。 假設線性系統的相關矩陣如下: 圖1 未知輸入dk的實際值 圖2是應用NRTSF得到的未知輸入估計結果圖。從中可以看出NRTSF能夠估計未知輸入d1k、d2k,但是對未知輸入d3k沒有估計效果,造成這一現象的原因是系數矩陣GK不滿秩。因此未知輸入d3k沒有影響到系統狀態,進而導致量測值中沒有未知輸入d3k的信息。 圖2 未知輸入dk的估計值 圖3和圖4分別是應用NRTSF得到的系統狀態的估計結果圖和系統狀態估計誤差結果圖,由于未知輸入分別加在前3個系統狀態分量,所以圖中分別給出了前3個系統狀態x1k、x2k和x3k的真實值、估計值以及估計誤差,由圖3和圖4可以看出狀態估計值都能夠跟蹤狀態真實值。 圖3 系統狀態及其估計值 圖4 系統狀態估計誤差 本文針對系統方程含有未知輸入的情況,討論了同時估計未知輸入和狀態的問題,針對經典濾波器的不足,提出一種新的三步迭代濾波器,其可以解決系統方程中未知輸入系數矩陣不滿秩時,經典濾波器無法使用的問題。仿真結果表明,新濾波器能夠有效估計未知輸入及系統狀態。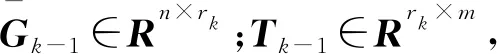
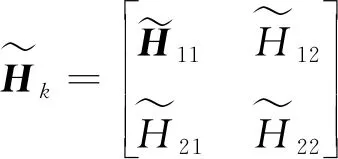
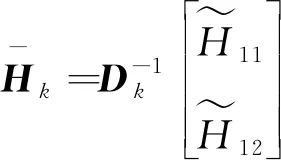
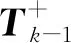

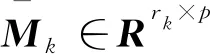
2.1 時間更新
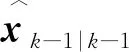
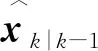
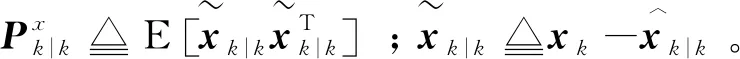
2.2 虛擬未知輸入估計
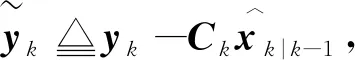
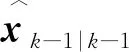
2.3 測量更新
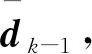
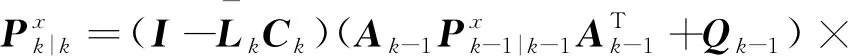
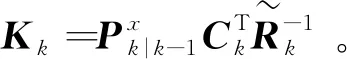
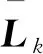
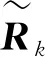
2.4 NRTSF迭代步驟總結
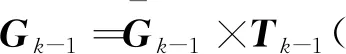
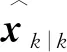
3 仿真結果分析

4 結語

