協作機器人的運動學誤差模型及標定算法

任彤，駱敏舟,，張佳麗

(1. 河海大學 機電工程學院，江蘇 常州 213022；2. 江蘇集萃智能制造技術研究所有限公司，江蘇 南京 211800)

0 引言

隨著機器人技術的提高與發展，智能機器人輔助、擴展及代替人類智能變成現代機器人技術發展的研究熱點。相較傳統工業機器人獨立的工作方式，人機協作領域的廣泛應用使協作機器人成為研發的前沿方向，而機器人的運行精度是描述其工作性能的重要指標之一。為了解決協作機器人重復定位精度優于絕對定位精度的共性問題，提高機器人絕對定位精度成為十分緊迫的任務。

絕對定位精度是指機器人運行到指定路點時目標位姿與期望位姿的精度偏差。針對人機協作的復雜應用場景，機器人運行軌跡不能簡單地通過示教方式實現，而是基于其他路徑規劃輔助工具，生成機器人運行過程中的工作位姿和軌跡，通過與機器人控制器的通信，控制實際運行姿態。除了在線規劃場景外，為實現對復雜路徑或重復路徑應用場景的高效作業，機器人通常采用離線編程方式完成相關任務的路徑規劃，生成可執行代碼程序導入控制機。上述作業的順利實現均要求機器人有高的絕對定位精度，若無法控制絕對定位精度，在作業過程中則無法實現預先設定的位姿軌跡，在人機協作要求較高的作業環境下，易引發事故。

為提高機器人絕對定位精度，一般采用誤差預防法和參數標定法兩種方式[2]。誤差預防法是指通過提高機器人的加工、裝配和控制精度，以控制實際參數與理論運動學參數間的誤差量來保證機器人定位精度。除了上述影響因素外，在機器人長時間運行過程中，機械結構發生的磨損與環境影響等原因[2]，各關節運動參數誤差傳遞到末端將嚴重影響末端運動精度。因此常用參數標定法辨識機器人實際運動學參數[3-5]，通過修正控制器中幾何參數的方式提高絕對定位精度。

1 運動學模型建立

首先分析機器人的模型結構與幾何參量，在1951年由DENAVIT J 和HARTENBERG R S[6]提出一種命名為D-H參數法的標準空間連桿機構的坐標構建方式，并在機器人領域中廣泛應用。各連桿間的位姿關系可通過桿長a、偏置d、桿扭轉角α和關節轉角θ四個參數確定，通過這四個參數描述桿件的自身集幾何參數和與相鄰連桿的空間關系[7]。基于D-H參數法，即可確定機器人相鄰各連桿間的變換矩陣，建立運動學模型。

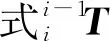
(1)

根據機器人設計的相應臂長和零位構型，分別如圖1(a)和圖1(b)，按照D-H建立關節坐標系，獲得機器人D-H參數，如表1所示。

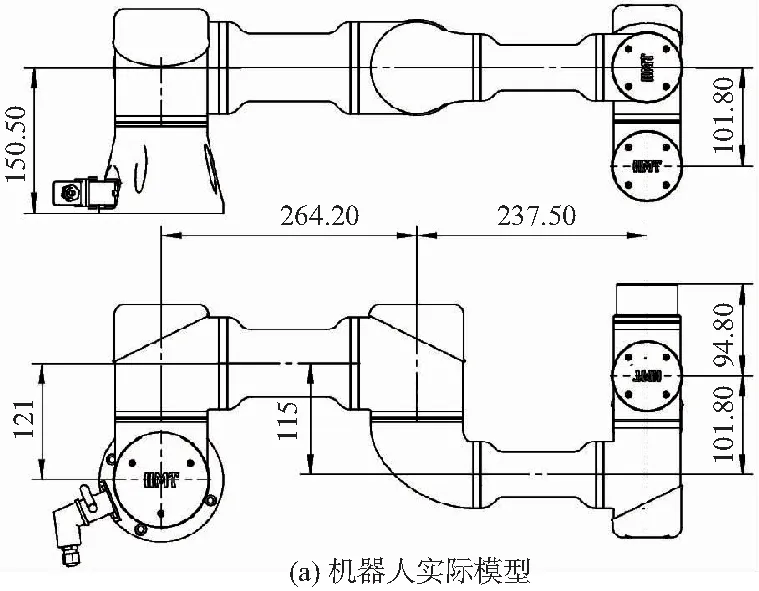
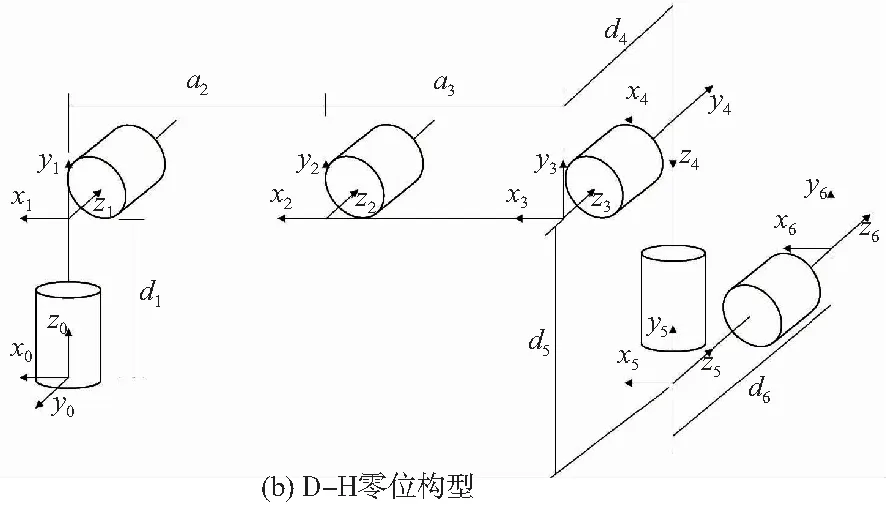
圖1 機器人實際臂長與D-H零位構型

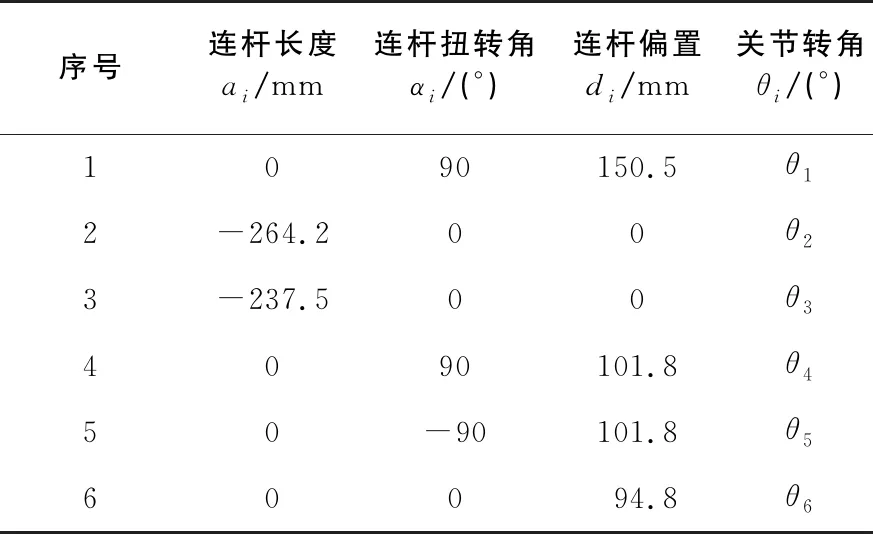
表1 D-H 參數表

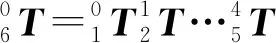
(2)

式中：n為法線矢量；o為方向矢量；a為接近矢量；n、o、a為相互垂直的正交單位矢量。向量p為機械臂末端連桿相對基坐標系的三維位置。

根據上述運動學正向模型與機械臂D-H參數，代入式(2)，可求解機械臂末端的空間位置：

(3)

式中：si和ci分別為sinθi和cosθi的簡寫形式，i=1，…，6。下文中sinθi和cosθi均以該形式簡寫，其中正逆解細則可參考文獻[8]。

在機器人參數標定過程中，機器人末端位姿的測量值主要用于機械臂幾何參數的辨識，同時由于機器人末端位置向量p可反映所需辨識參數ai、αi、di和θi的誤差，因此在辨識過程中僅測量末端空間位置，不考慮末端姿態。

2 機器人參數標定

機器人參數標定可分為關節級標定、運動學參數標定和動力學參數標定三個部分[8]。第一部分關節級標定指確定機器人實際關節轉動角度與理論轉動角度關系，該級精度可通過分析關節理論運行位置與位置傳感器信號間的正確關系，測量實際運行中的偏差量獲得；第二部分為機器人運動學參數的標定，運動學參數誤差包括機器人機構D-H精度，零位標定誤差等各連桿間的幾何參數誤差；第三部分為機器人動力學標定，針對機器人動力學模型誤差、各連桿的負載和慣性參數、關節模組柔性機構誤差、機構間隙摩擦等各參量進行標定辨識。

考慮各誤差參數的可辨識性與誤差對絕對定位精度的影響程度，本文在建立誤差模型時忽略影響相對較小的因素，同時由于所辨識機器人數學模型為運動學模型，因此主要對第二級機器人運動學參數進行矯正。

根據D-H參數的運動學模型，機械臂末端位置精度依賴于各連桿關節處運動學參數ai、αi、di和θi，而在扭轉角αi與機器人整體構型相關不加入誤差模型建立，因此基于正解模型，相鄰連桿間的位姿微小偏差可被Δai、Δdi和Δθi描述。運動學模型建立的基礎上，利用微分運動的思想，求解相鄰連桿間的誤差矩陣，通過齊次矩陣的連乘計算末端的運動學誤差模型。

2.1 相鄰連桿間位姿誤差

已知相鄰連桿齊次轉換矩陣如式(1)所示，誤差項可表達為：

(3)

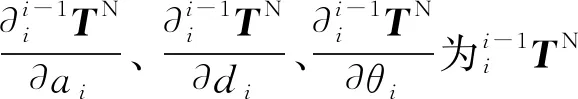
根據全微分定理可得：

(4)

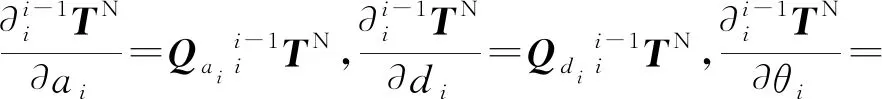
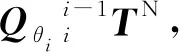
(5)

將式(4)和式(5)代回式(3)中，可得：

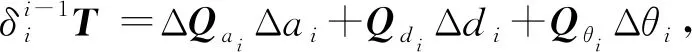
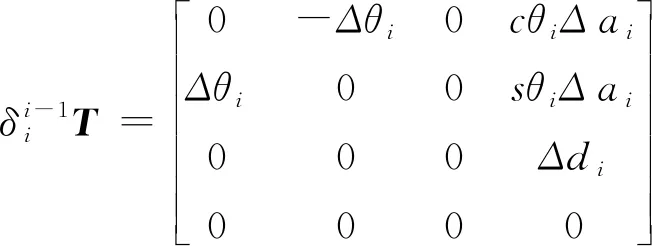
(6)

2.2 微分運動

由于幾何參數的誤差，末端實際位置與理論位置存在誤差，該誤差可通過微分運動學描述。微分運動[9]分為微分平移Trans(dx，dy，dz)與微分旋轉Rot(k，dθ)兩部分，將微分旋轉部分分解為繞原坐標系x、y、z軸分別旋轉δx、δy、δz，且由于偏轉角度為一較小值，因此sinδx=δx，cosδx=1。誤差項可由微分旋轉矩陣表示為：

TR=TN+dT=Trans(dx,dy,dz)Rot(x,δx)Rot(y,δy)Rot(z,δz)TN

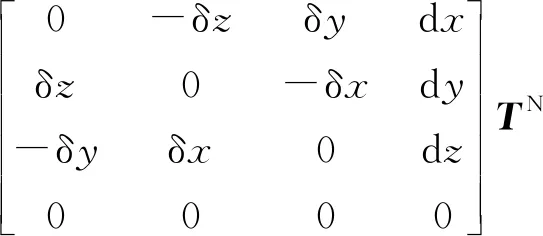
定義ΔT=Trans(dx, dy, dz) Rot(k, dθ)-I4,得

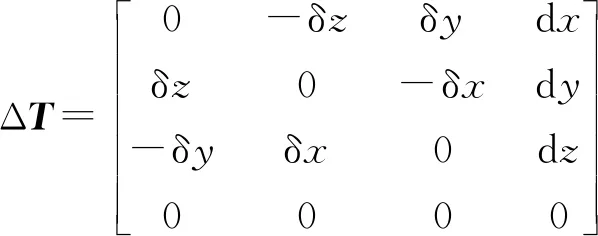
(7)

微分變化ΔT由平移矢量dp和旋轉矢量δk組成，同時將式(6)代入可得：

(8)

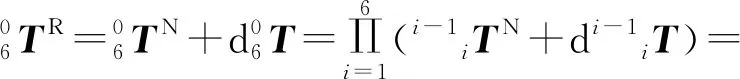
(9)

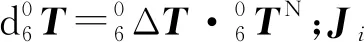
(10)

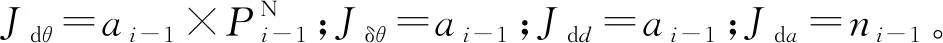
2.3 運動學誤差模型

建立精準完善的誤差模型是機器人幾何參數辨識的重要前提。搭建的機器人標定平臺如圖2所示。

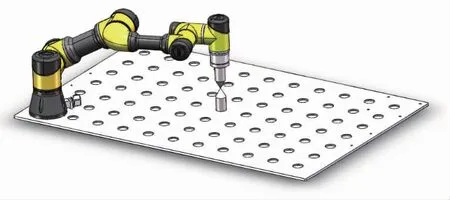
圖2 機器人標定平臺

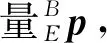
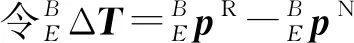
(11)

其中Δa1、Δa4～Δa6、Δd2、Δd3為無需辨識參數，另其系數項為0。

3 實驗

運動學參數辨識是將機器人末端位姿誤差作為輸入量，通過誤差模型進行參數的曲線擬合。典型的測量方法包括伸縮式球桿儀[10]、光學跟蹤法[11]、激光跟蹤儀[12]、平面約束法[13]等多種。本實驗為測量末端誤差，將機器人安裝在有孔的硬板上，安裝位置和基座坐標方向與標定板零位重合，實現無外部傳感的標定方式，根據所設計的標定板(圖3)，可進行兩種方式的校準：

1)根據標定板各個位置點信息，將機器人移到正確位置，使工具末端與標定板槽口對齊，假設底面平行且完全重合，以此確定工具末端中心在世界坐標下的絕對位置。

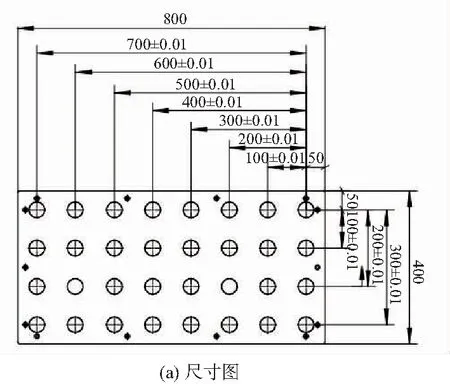
圖3 標定板尺寸與實物圖

2)安裝如圖2所示的機器人末端尖端，移動機器人令工具末端尖端與標定板上所安裝的尖端完全重合，由于所安裝尖端尺寸與工具末端尺寸已知，即可獲得工具末端中心在世界坐標下的絕對位置。以上兩種校正方式均要求較高精度，在進行曲線擬合前，需注意生成的統計數據，以免影響校準精度。

本實驗采用第二種校準方式，控制機械臂在不同的姿態下觸碰標定板上的尖端，通過尖端完全重合來保證工具末端位置不變，姿態變化不影響計算精度，記錄20組數據，記錄各組所對應的機械臂各關節編碼器值。

將這20組點依次進行運動學正解，獲得在初始化參數下各點對應的末端理論位置值。得到的末端執行器在相對世界坐標系下的實際位置與目標位置的誤差如圖4所示。

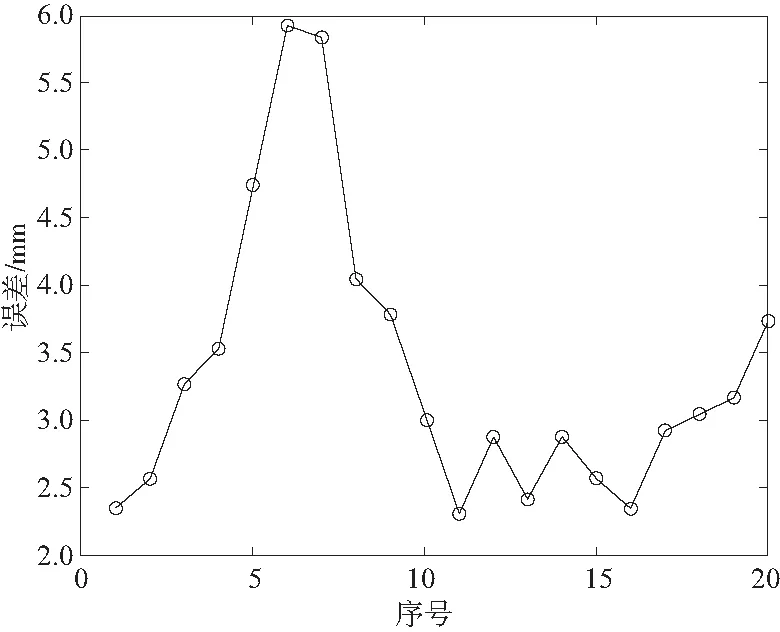
圖4 標定前各組數據誤差

補償前機器人工作末端的絕對定位誤差平均誤差為3.365 mm，其中最大值誤差為5.923 mm。根據實際誤差將其系數矩陣行奇異值分解，利用最小二乘法對機器人幾何參數誤差進行辨識，根據式(11)求解運動參數誤差值，結果如表2所示。

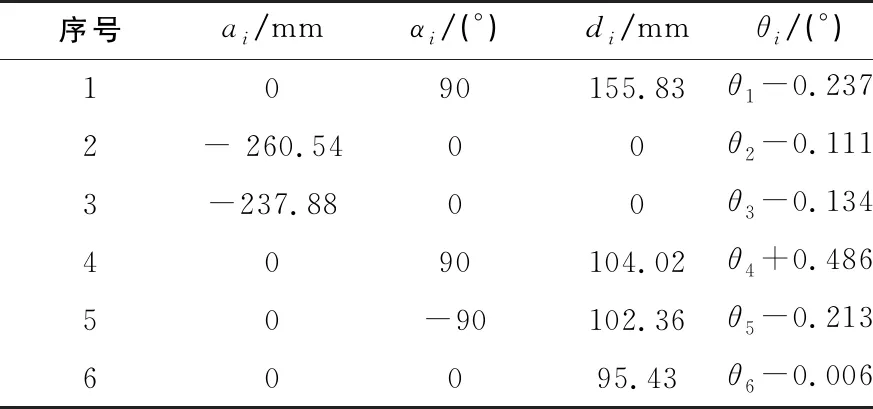
表2 修正后D-H 參數表

機器人誤差補償的主要方式分為兩種，針對控制器開放的機器人通過修改控制器中底層模型運動學參數的方式實現，針對不開放控制器的機器人可通過外部補償方式，將辨識后的真實參數寫入，根據新的運動學模型通過正運動學重新計算優化后的機器人末端位置參數，與實際位置進行比較，結果見圖5。

圖5 標定后各組數據誤差

補償后工作末端的絕對定位誤差平均為1.689 mm，其中最大值為3.512 mm。通過圖4與圖5對比可得，經過對機器人幾何參數的補償，其絕對定位精度得到了明顯的提高，但在數據處理時可發現第6、第7兩組數據誤差較大，影響參數辨識。因此在數據處理時將這兩組數據忽略，重新計算可得表3、圖6數據。

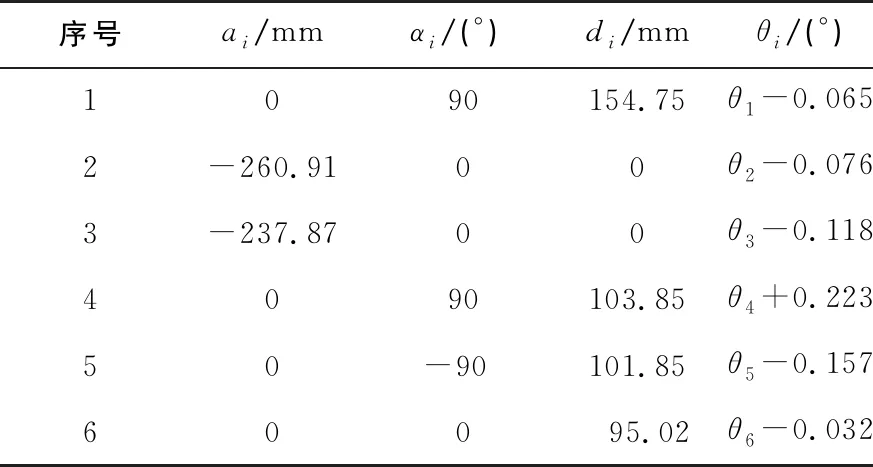
表3 數據處理后標定D-H 參數表

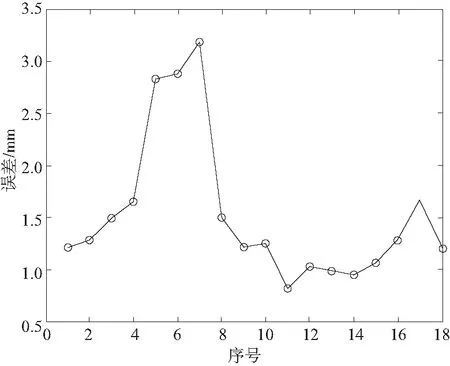
圖6 數據處理后各組數據誤差

經過數據剔除后，工作末端的絕對定位誤差平均誤差達到1.528 mm，其中最大值為3.182 mm，由此可得本運動學參數標定方法受輸入數據精度影響，并非所有的校準都是好的校準，在標定時應注意生成的統計信息。若輸入數據誤差太大，機器人標定后的絕對定位精度可能會變得不準確。

4 結語

本文主要研究了六自由度協作機器人的運動學參數標定方法及過程，分析絕對定位精度誤差來源，建立機器人微分方程，提出基于機器人工具末端的運動學誤差模型建立方法，利用標定板獲取機器人工具末端位置信息誤差，采用最小二乘法求解誤差方程。結果表明該補償方式可提高絕對定位精度，由補償前的3.365 mm降為補償后的1.528 mm。