支承方式對轉子動力學特性影響研究
李鴻梅,張洪信,趙清海
(青島大學 機電工程學院,山東 青島 266071)
0 引言
隨著社會生活水平的提高和人們環保意識的增強,新能源的燃料電池汽車得到了較大的發展。燃料電池所用的空氣壓縮機需要極高轉速的電機,而高速電機運轉過程中產生的振動和噪聲問題也得到了大家的廣泛關注[1-3],其中,轉子系統的支承方式是重要影響因素。
某型燃料電池空氣壓縮機用高速永磁同步電機具有質量輕、體積小、轉速高等優點,其轉子系統由磁鋼、鋼套、轉子芯軸、葉輪、軸承以及螺母構成,額定轉速為60000 r/min。電機的轉速很容易接近臨界轉速而引發共振,使得電機強烈振動,也會產生很大的噪聲,嚴重時還有可能導致轉子損壞或者失速。這與轉子系統的支承方式有著很大的關系,因此十分有必要進行電機轉子系統在不同支承方式下的動力學特性研究[4-5]。在進行動力學分析時要建立精確的軸系有限元模型,同時還要對轉子結構進行專門的簡化處理,將對結果影響很小的微小邊角特征去掉[6]。
本文對轉子的動力學特性進行了理論分析,采用有限元分析軟件ANSYS workbench,將轉子系統劃分為芯軸、磁鋼、鋼套、集中質量、轉動慣量和軸承支承等單元,分別求解了軸承剛性支承和軸承彈性支承時轉子系統的振型、固有頻率及臨界轉速,得出了坎貝爾圖,計算了臨界轉速的避開裕度,驗證了轉子系統的安全性,并分析了轉子在不同剛度系數的彈性支承軸承作用下臨界轉速的變化情況,總結其規律,為轉子系統動力學特性的優化提供了理論支持。
1 轉子結構及動力學分析原理
1.1 轉子系統結構組成
本文所述高速永磁同步電機的轉子結構示意如圖1所示,主要由磁鋼、鋼套、芯軸構成。其中,圖中所標1與7處為螺母,2、5、6處為葉輪,3與4處為無接觸軸承支承。為了方便進行下一步的轉子動力學特性的有限元仿真分析,將高速轉子模型進行簡化處理,刪除掉螺栓孔、邊沿倒角、圓角等微小特征。轉子的額定工作轉速為60000 r/min,總長為266 mm,總質量為1.29 kg。
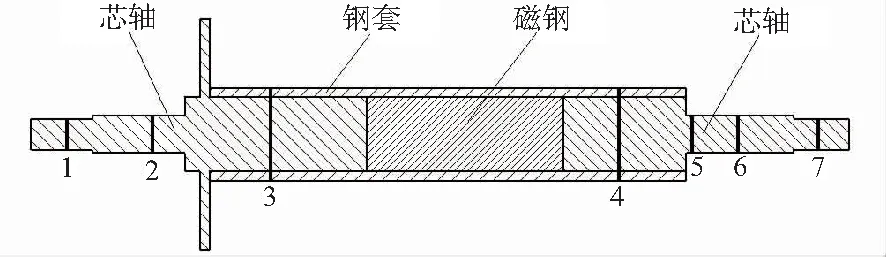
圖1 高速轉子結構圖
轉子系統各部件的材料特性、參數如表1所示。
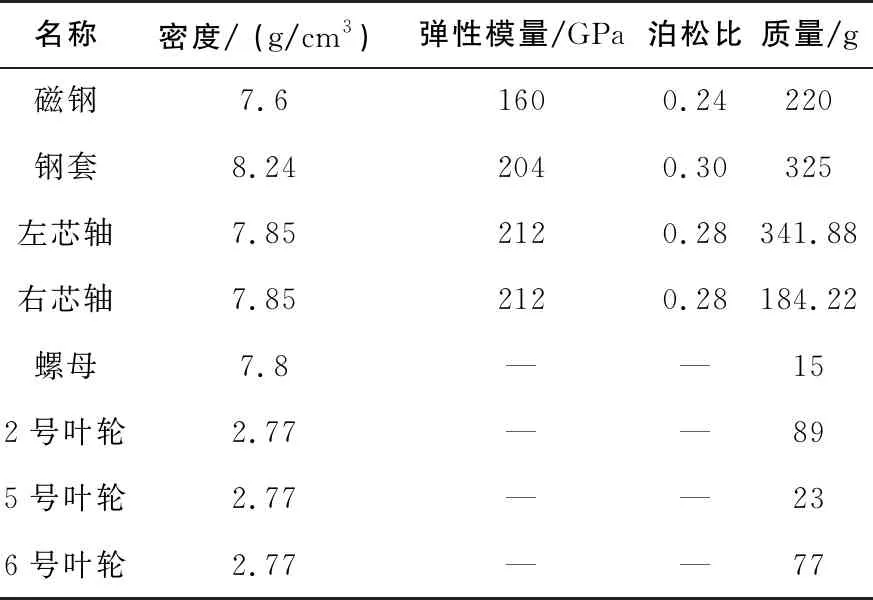
表1 轉子系統各部件參數
1.2 模態分析原理
轉子系統的運動微分方程可表示為
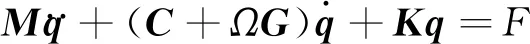
(1)
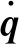
在轉子動力學特性分析中,為了便于求解,常將式(1)的二階線性微分方程改寫為如下的狀態-空間形式[7]:
(2)
求解式(2)便可以得到在任意激振力F作用下轉子系統的動力學響應。
2 轉子動力學特性有限元分析
2.1 轉子系統動力學模型建立
利用三維建模軟件建立轉子系統的三維模型,為簡化模型,去掉數值較小、對于轉子動力學特性分析影響較小的邊沿倒角、圓角等特征。在基于有限元法的動力學分析軟件中導入轉子模型,考慮陀螺效應,根據轉子系統動力學離散建模簡化方法[8],將空氣壓縮機的葉輪以集中質量和轉動慣量的形式等效到其在轉子上的質心處。螺母也以相同的方法處理,輸入具體的質量參數與轉動慣量參數值,軸承利用有限元軟件建立,改變軸承的剛度參數、阻尼參數數值以及支承方式來進行轉子系統的動力學特性研究。
轉子系統的動力學計算模型如圖2所示。

圖2 轉子系統的動力學模型
2.2 轉子系統振型顯示
模態是具有無窮階的,但是對于運動起主導作用的只是低階模態,因此只提取前幾階模態進行分析。模態分析可以直觀地得到轉子系統的固有頻率和振型,軸承剛性支承時轉子的前兩階振型如圖3、圖4所示。

圖3 剛性支承轉子一階振型圖

圖4 剛性支承轉子二階振型圖
可以看出:在軸承剛性支承的工況下,轉子一階振動時,右芯軸最右端變形最大;轉子二階振動時,左芯軸最左端變形最大。
以軸承剛度系數為3000 N/mm為例,軸承彈性支承時轉子的各階振型如圖5-圖8所示。

圖5 彈性支承轉子一階振型圖

圖6 彈性支承轉子二階振型圖

圖7 彈性支承轉子三階振型圖

圖8 彈性支承轉子四階振型圖
可以看出:在軸承彈性支承的工況下,轉子一階振動時,左芯軸最左端變形最大;轉子二階振動時,右芯軸最右端變形最大;轉子三階振動時,左右芯軸兩端變形都較大,最大變形位于右芯軸最右端;轉子四階振動時,同樣地,左右芯軸兩端變形都較大,但彎曲方向與三階時相反,最大變形位于左芯軸最左端。
3 轉子系統模態分析結果
3.1 軸承剛性支承時的固有頻率和臨界轉速
當軸承為剛性支承時,對轉子系統進行模態分析所得到的各階固有頻率和臨界轉速如表2所示。轉子系統的前兩階固有頻率分別為2020 Hz和2354.6 Hz,其中,Mode1和Mode2為一階重復頻率,Mode3和Mode4為二階重復頻率,這是因為轉子具有對稱性,因此它會有重合的頻率。轉子系統的前兩階臨界轉速分別為122830 r/min和143930 r/min,其中,Mode1為一階反進動,Mode2為一階正進動,Mode3為二階反進動,Mode4為二階正進動,正進動所對應的為臨界轉速。前兩階臨界轉速對電機轉子系統的最高轉速85000 r/min的避開裕度分別為44.5%和69.3%,遠>20%的安全范圍,工作時不會發生共振現象[9]。

表2 剛性支承轉子系統的模態分析結果
剛性支承轉子系統的坎貝爾圖如圖9所示,從頻率軸出發斜率為正的曲線為同步正進動曲線,斜率為負的曲線為同步反進動曲線,從原點出發的直線為一倍頻線,一倍頻線與正反進動曲線的交點對應的橫坐標即為臨界轉速,通常只考慮正進動時的臨界轉速。在圖9中,一倍頻線與Mode2、Mode4進動曲線的交點分別對應一階振動與二階振動的臨界轉速。
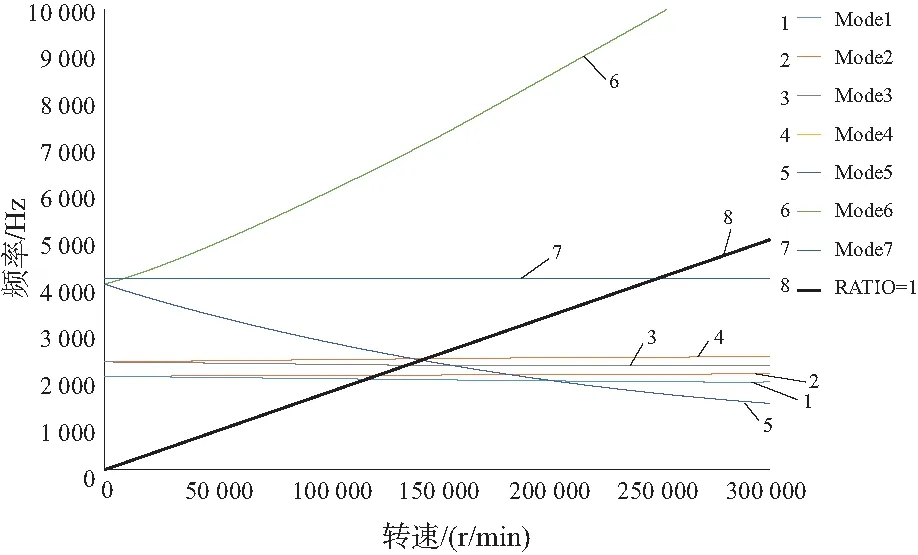
圖9 剛性支承轉子系統的坎貝爾圖
3.2 軸承彈性支承時的固有頻率和臨界轉速
當軸承為彈性支承時,以軸承剛度系數為3000 N/mm為例,對轉子系統進行模態分析所得到的各階固有頻率和臨界轉速如表3所示。轉子系統的前三階固有頻率分別為284.98 Hz、346.95 Hz和1880.2 Hz,其中,Mode1和Mode2為一階重復頻率,Mode3和Mode4為二階重復頻率,Mode5和Mode6為三階重復頻率。轉子系統的前三階臨界轉速分別為17352 r/min、20847 r/min和116150 r/min,其中,Mode1、Mode3、Mode5為反進動,Mode2、Mode4、Mode6為正進動。前三階臨界轉速對電機轉子系統的轉速范圍30000 r/min~85000 r/min的避開裕度分別為42.16%、30.51%和36.65%,均>20%的安全范圍,不會發生共振現象。
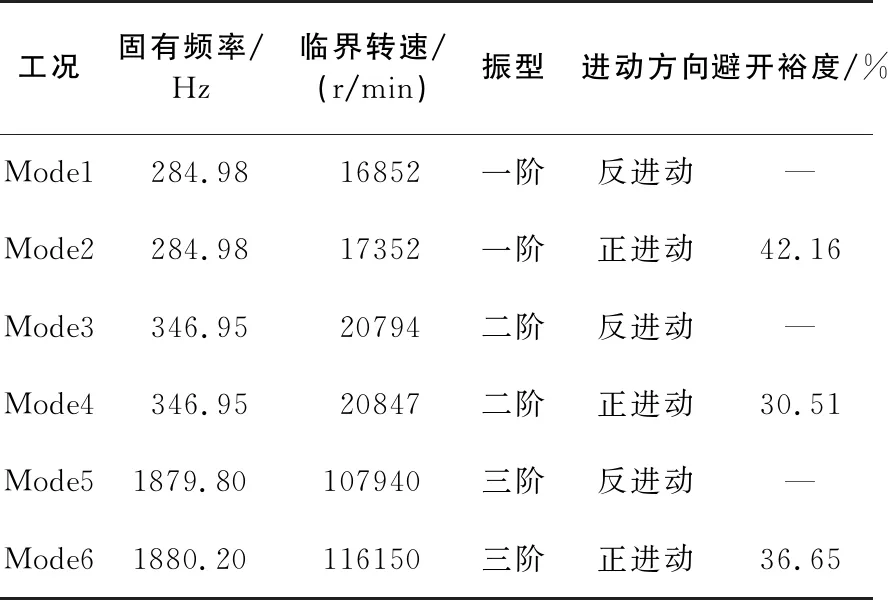
表3 彈性支承轉子系統的模態分析結果
彈性支承轉子系統的坎貝爾圖如圖10所示,一倍頻線與Mode2、Mode4、Mode6進動曲線的交點分別對應前三階振動的臨界轉速。
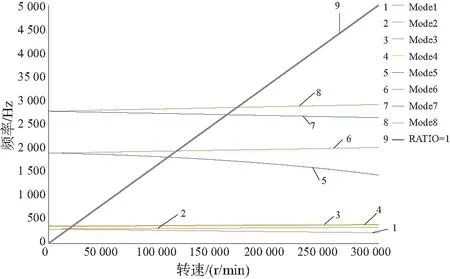
圖10 彈性支承轉子系統的坎貝爾圖
3.3 轉子軸承剛度對臨界轉速的影響
轉子系統的彈性支承軸承剛度從3000 N/mm到12000 N/mm變化,不考慮軸承阻尼系數的影響,計算轉子的前三階臨界轉速及其對轉子轉速范圍30000 r/min~85000 r/min的避開裕度如表4所示。
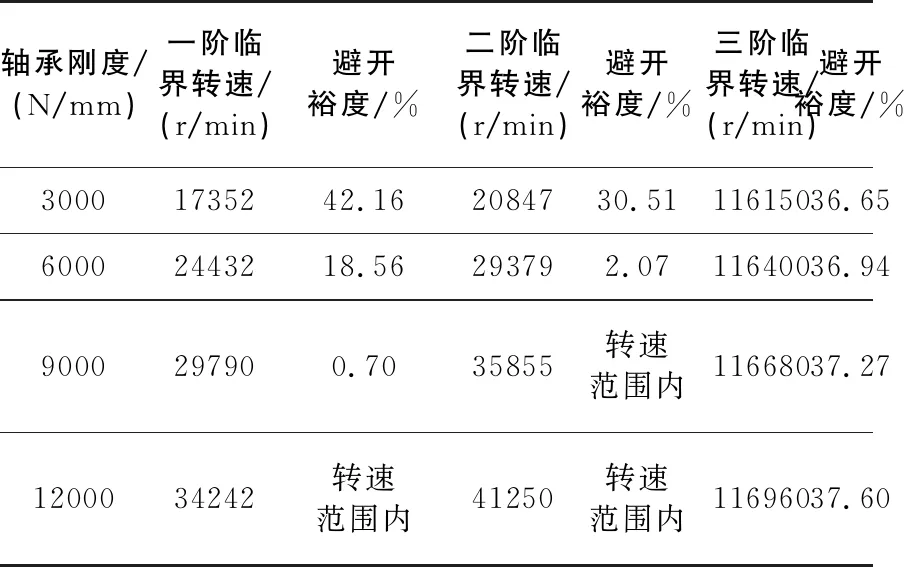
表4 轉子軸承剛度對臨界轉速的影響
由表4可以看出,隨著軸承支承剛度的增大,各階轉子臨界轉速均有所提高,三階臨界轉速數值變化相對較小。一階臨界轉速的避開裕度隨著軸承剛度的增加而降低,當軸承剛度為12000 N/mm時,一階臨界轉速落入轉子的轉速范圍內,但其對轉子額定轉速60000 r/min的避開裕度為42.93%。在轉子提速過程中應注意規避臨界轉速,快速到達額定轉速即可平穩運行。二階臨界轉速在軸承剛度為9000 N/mm時即落入轉子的轉速范圍內,軸承剛度為9000 N/mm和12000 N/mm時,二階臨界轉速對轉子額定轉速的避開裕度分別為40.24%和31.25%,均>20%。三階臨界轉速的避開裕度隨著軸承剛度的增加而增大。
4 結語
1)軸承剛性支承時的前兩階臨界轉速要遠高于軸承彈性支承時相對應階數的臨界轉速值。
2)通過對轉子系統進行模態分析可以得到轉子的各階振型、固有頻率和臨界轉速,計算可得出不同工況下臨界轉速對轉子轉速的避開裕度,選擇軸承時要確保避開裕度>20%。
3)轉子系統的臨界轉速會隨著軸承剛度系數的增大而增大。
4)高速轉子通常需進行動平衡試驗,但實現高速運轉成本高,所以在試驗中一般不會達到轉子的實際最高運轉速度。通過試驗臺上較低轉速的試驗來驗證有限元模型仿真結果的準確性,再依據有限元仿真結果來估計高階的臨界轉速,避免轉子在實際運轉過程中產生共振。因此有限元模型的仿真結果對實際工作具有一定的指導意義。

