一種三自由度仿生咀嚼機器人的建模與分析

曹安琪，薛建彬

(南京航空航天大學 機電學院，江蘇 南京 210016)

0 引言

咀嚼能力是影響人們消化食物進行營養吸收的重要因素，在實際臨床中，或因不同的口腔損傷問題，造成了一部分人的咀嚼障礙難題。國內外學者對此設計出了不同功能的輔助咀嚼機構，統稱咀嚼機器人，它可以模擬人類的咀嚼行為，從而幫助醫生進行咀嚼運動的研究或幫助患者進行康復訓練等。

英國布里斯托爾大學的專家學者們基于Stewart平臺研究了六自由度并聯機構咀嚼機器人Dento-Munch，它利用6個獨立的驅動器模擬人類咀嚼模式，代替下顎周圍的咀嚼肌控制下顎平臺的運動[1-2]。叢明等人根據人類下頜骨的生物力學結構，利用線性驅動器替代咬肌、顳肌和翼狀肌3組肌肉，通過建模與對機器人的運動學分析，設計出了新型咀嚼機器人[3]。

目前，大多數咀嚼機器人是由多電機驅動，雖然可以更好地模擬出人的不同咀嚼軌跡，但是實際上其功能有些冗余。如何將復雜的六自由度咀嚼機器人在不影響基本咀嚼功能的基礎上進行簡化設計，本文提出一種三自由度的咀嚼機器人[4]，將3根驅動桿置于不同平面上，與人類口腔架構吻合度更高，基本可以實現切碎、研磨等功能。

1 三自由度仿生咀嚼機器人的建模

人體的咀嚼運動是三維的，可分為兩個階段，切碎與研磨[5]，因此口腔的張合運動和左右運動基本決定了咀嚼運動的進行，而另外的運動則主要是輔助完成咀嚼運動，但是對咀嚼功能的影響相對于這兩個運動的影響要小得多。本文咀嚼機器人的設計主要需要實現的就是這兩組運動，不難解析出，機構運動的實現需要3個自由度。

常用的三自由度運動機構主要是3-PSR并聯機構[6-7]，該機構主要由3組運動副構成。參照這樣的設計理念，對咀嚼機器人進行設計，如圖1所示。外部框架模擬人類的口腔結構，為固定平臺，將上頜骨固定在固定平臺上，下頜骨與3個驅動液壓桿通過球副連接，液壓桿通過鉸鏈連接在支座上，驅動桿的設計如圖2所示。

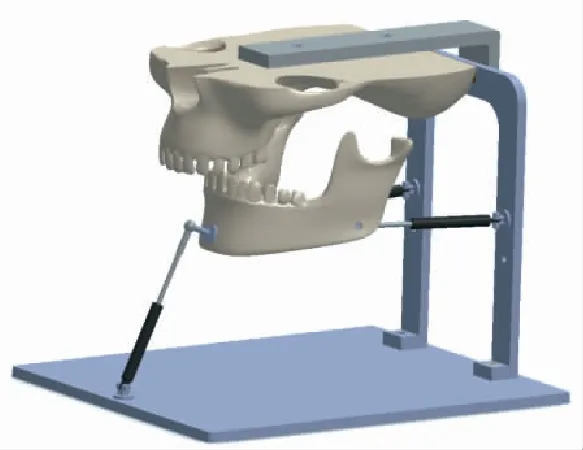
圖1 三自由度牙齒外骨骼機器人機構圖

圖2 驅動桿設計圖

2 三自由度仿生咀嚼機器人的運動學計算與仿真分析

2.1 三自由度仿生咀嚼機器人的運動學計算

為了描述機器人的運動，設參考坐標系O-xyz與定平臺相連。與定平臺相連的轉動副為B1、B2、B3，xy平面與B1所在平面重合，x軸平行于B2B3連線指向B2，y軸垂直于B2B3連線指向B1，z軸垂直于B2B3連線豎直向上。設相對坐標系O′ -x′y′z′與下頜相連，x′y′平面與3個球副連接點所構成的平面重合，球副為b1、b2、b3，x′軸在b2b3連線上指向b2，y′垂直于b2b3連線指向b1。根據右手定則，可以確定z′軸的方向，如圖3所示。設B2、B3距離為2d1，B1到x軸距離為d2，B2、B3到x軸距離為d3，如圖4(a)所示，則B1、B2、B3的坐標分別為B1[0，d2,0]、B2[d1，0,d3]、B3[-d1，0,d3]。同理，如圖4(b)所示，b1、b2、b3的坐標分別為b1[0，d5,0]、b2[d4，0，0]、b3[-d4，0，0]。

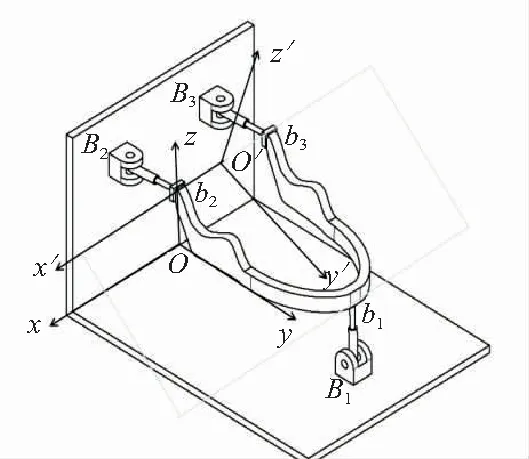
圖3 咀嚼機器人結構圖

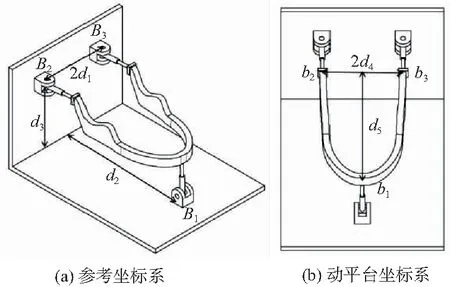
圖4 咀嚼機器人坐標系示意圖

1)機構的位置反解

機構的位置反解指已知機構的最終位姿，先進行驅動輸入狀態的反求過程[8]。首先，通過動平臺的3個旋轉運動，將動坐標系旋轉到與定坐標系3個軸的方向都一致的位置，將O′-x′y′z′繞著x′、y′、z′軸朝逆時針方向分別旋轉α、β、θ，此時齊次變換矩陣可以表示為：

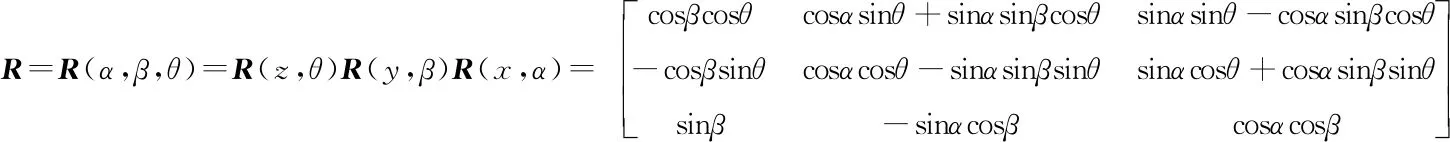
當動平臺的坐標系3根軸經過旋轉與定坐標系的3根軸方向一致，那么再經過平移，兩個坐標系即可重合，設平移向量為OP=[x,y,z]T。由于設計的咀嚼機器人是三自由度的，只能繞著x軸和z軸進行旋轉，沿著y軸進行平移，即β=0，x=0，z=0，此時，有

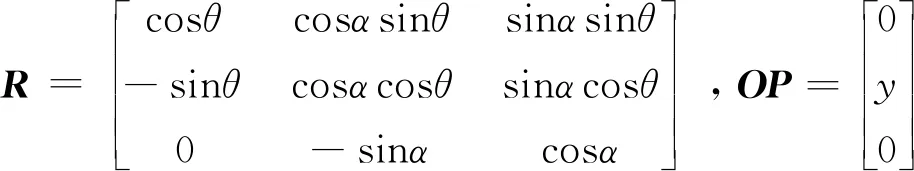
假設動平臺位姿確定，則各個驅動桿li(i=1,2,3)的表示方法即可確定，有：

li=Bibi=R[xbi，ybi，zbi]+OP-[xBi，yBi，zBi]

用Li(i=1,2,3)表示各個驅動桿的長度，聯立則可得到機構的位置反解結果，即：

則有：

由上式可以看出，機構的位置反解是3個獨立的方程，且d1、d2、d3、d4、d5均為已知量，并且當機構的位姿坐標(α，0，θ，0，y，0)確定的時候，機構的驅動桿的輸入也是唯一確定的，機構的位姿反解就可以通過上式求得。

2)機構的位置正解

與機構的位置反解相反，機構的位置正解指的是已知機構驅動桿的輸入，進行機構最終的位姿狀態求解的過程[9]。對于本文的咀嚼機器人，機構的位置正解指的就是已知3根驅動桿的輸入，求解下頜的運動姿態。

為了計算簡便，將機構正解所得的非線性方程組進行化簡，化簡后為：

由上式可以看出，機構的位置正解也是3個獨立的方程，當機構的輸入為li(i=1,2,3)時，代表著機構的輸入已知，則各驅動桿的長度Li(i=1,2,3)已知，方程中只剩下α、θ、y這3個未知量，方程解可以求得，即為機構的位姿解，則機構的位置正解完成。

2.2 三自由度仿生咀嚼機器人的仿真分析

少自由度并聯機器人的運動大多具有不確定性，因此，在實際投入使用前，需要進行仿真分析。首先將模型導入ADAMS軟件并添加約束，在本次的ADAMS仿真分析中，x軸在顳下頜骨連線上，y軸為機構的垂直軸，z軸垂直于顳下頜骨連線并指向下切牙方向。

1)下頜張合運動仿真結果分析

下頜張合運動指的是下頜繞著顳下頜骨連線的上下轉動，因此，y方向的驅動條件設置為sin(2×π×time)×L，其中L為參考點與運動輸入的驅動點間的距離，x、z方向固定。選擇下頜質心為運動參考點，標記為Marker79，對這個點添加運動驅動。由于仿真過程為動態過程，不便展示，因此使用下頜上的運動輸入的驅動點位移曲線來代表，如圖5所示。

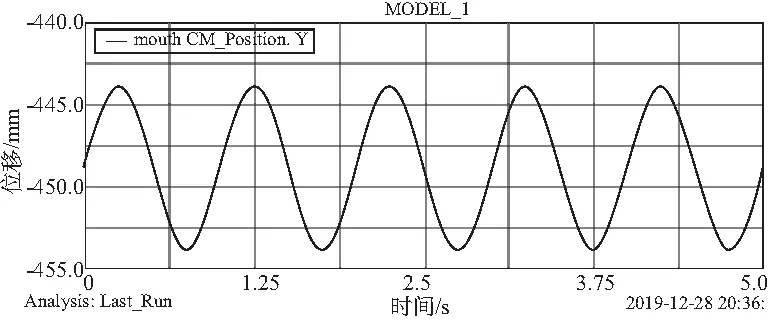
圖5 下頜上參考點運動輸入的驅動曲線圖

將下頜的張合運動模擬為z軸固定，則只有豎直方向的液壓桿參與了運動，此液壓桿的驅動輸入見圖6。由位移-時間曲線可以看出，在y方向上，液壓桿的運動類似于正弦函數，最大運動幅度約為30 mm，在z方向上也存在類似正弦的運動，運動幅度較小，最大幅度約為0.6 mm，相比于y方向上的運動可以忽略不計。如忽略機構本身的抖動及摩擦力等干擾因素，當運動平臺的參考點運動輸入為正弦函數的時候，液壓桿的位移變化較為平穩，輸入也為正弦函數，變化周期同樣為2。前文中運動學的位置反解公式已經求出，將參考點的運動輸入代入，結果與ADAMS仿真結果一致，說明了分析的正確性與機構的可行性。

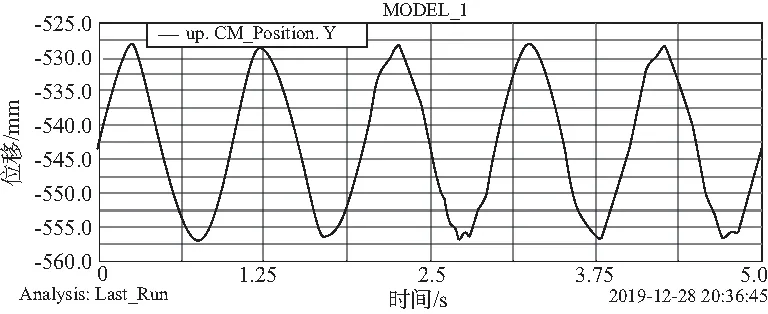
圖6 液壓桿y軸方向上位移-時間曲線

2)下頜側方運動仿真結果分析

側方運動指下頜繞著垂直軸的左右轉動，因此可賦予一個圍繞著y軸、以前液壓桿為參考點的旋轉運動作為驅動條件，驅動函數為disp(y)=0.05×sin(1.256×time)。對Marker79即下頜上的參考點添加點驅動，下頜的側方運動是通過兩個液壓桿的配合來實現運動的。為了便于分析，將底板上的液壓桿作為固定支點，因此側方運動在z軸并沒有發生位移，所以側面基板上兩個液壓桿在z軸方向上的運動應該是相反的，仿真結果如圖7所示。兩個液壓桿z軸的運動曲線呈對稱，因此位移剛好抵消，實現下頜動平臺z軸方向上的零位移。

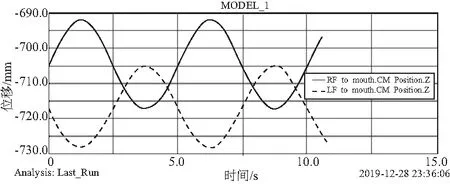
圖7 側面基板上兩個液壓桿z軸方向上位移-時間曲線

下頜的側方運動不僅在z軸方向上存在位移，在x軸方向上也同樣有著一定的位移關系，但是由于側方運動是沿著豎直液壓桿的旋轉運動，因此兩水平液壓桿的x位移應該保持一致，仿真結果同樣驗證了這個理論，結果如圖8所示。

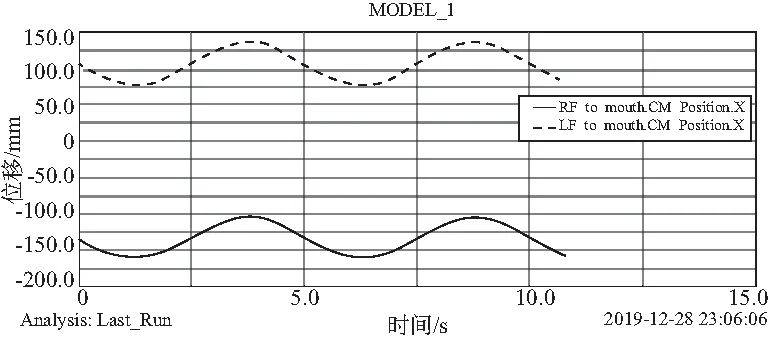
圖8 側面基板上兩個液壓桿x軸方向上位移-時間曲線

3 結語

本文基于人類口腔架構與人類咀嚼方式等特征，設計了一種三自由度仿生咀嚼機器人。機器人由三組驅動桿構成，每一組驅動桿由一個移動副，一個轉動副以及一個球副組成，整個機器人具有三個自由度。完成機器人建模后，對機器人的切碎和研磨兩個過程進行運動學計算與仿真分析，驗證了設計的仿真機器人可以實現的切碎以及研磨運動的幅度，切碎方向最大幅度為30 mm，研磨方向最大幅度為20 mm，可以滿足口腔實際的運動仿真。