球凹/球凸結構對小尺度通道換熱影響研究
王鵬恩, 岳晨,童樂,張世中
(南京航空航天大學 能源與動力學院,江蘇 南京 210016)
0 引言
液體火箭發動機能為航天器提供強大的推力,從而滿足人類太空探索的需要。但是發動機在運行時,內部的高溫氣流對燃燒室內壁產生劇烈的沖刷,使得壁面發生燒蝕并破環壁面結構。因此,需要采用有效的冷卻手段對發動機壁面進行冷卻[1-2]。
再生冷卻作為一種發動機冷卻技術,近些年已有部分文獻對其進行報道[3]。ZHANG S L等[4]和王敏飛[5]模擬了不同通道長寬比對流動換熱的影響,研究發現當冷卻通道為方形最有利于管道內的流動換熱。另外研究人員對常規通道中添加肋進行了研究[6-9],金光等人[6]討論了圓柱形肋高和肋角度對換熱的影響。WANG C L等人[8]發現球凸在強化換熱的同時,可將壓力降低到可接受的范圍。AFANASYEV V N等人[9]研究了球凹的換熱性能及其流動損失特性,結果表明球凹相對光滑表面換熱能力增加了30%~40%,而壓力損失僅略有增加。
雖然目前已有部分文獻對肋的換熱研究進行了報道,但是對于液體火箭發動機的再生冷卻通道研究大多是關于通道外部結構,而對于通道中添加肋的研究很少,且現有的研究也存在通道高壓降的問題。由文獻[10]可知,仿真對于物體的熱防護是可行的,所以本文利用Fluent軟件,根據球凹低壓降的特性,研究一種球凹/球凸結構對流動換熱的影響。
1 數值模擬
1.1 數值模型驗證
本研究數值模型驗證參考XIE P Y等人[11]的驗證方法,文中提到實際的再生冷卻通道為矩形結構,但公開文獻中還沒有關于矩形管中氫流動的相關實驗。所以利用文獻[12]中的氫燃料在圓管中的流動實驗數據進行數值模型驗證,并參照該文獻中RUN75-666組實驗數據進行數值模型驗證。驗證結果如圖1所示。
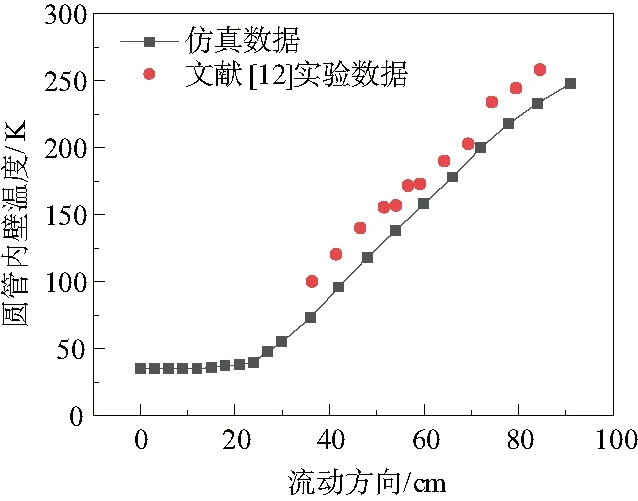
圖1 數值模型驗證
驗證結果表明:在Fluent中利用Real Gas Peng Robinson方程定義密度可以很好地預測超臨界下流體密度的變化;另外湍流模型采用SST模型,壓力和速度的耦合采用標準SIMPLE方法對氫燃料在湍流下的流動模擬中是可行的。
1.2 矩形通道模型驗證
由于在公開的文獻中還未見到單排添加球形結構的實驗,所以本研究參考王強[13]的驗證方法,與文獻[14]中的光滑矩形通道管內流動實驗數據進行對比,實驗中工質為不可壓空氣,雷諾數Re為14 767,以通道努塞爾數為參考依據,結果如圖2所示,可以看出仿真和實驗數據基本吻合,說明了此數值方法模擬矩形管內流動是可行的。
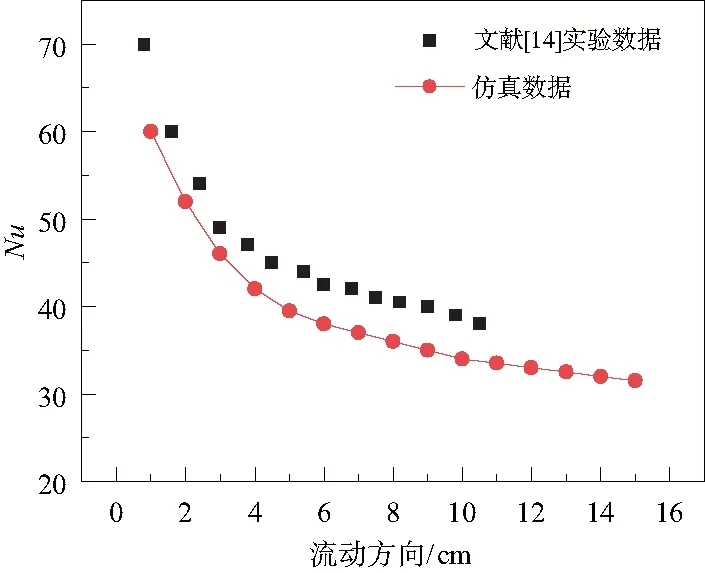
圖2 矩形通道模型驗證
1.3 計算模型簡介
如圖3所示為本研究的仿真模型,單位為 mm。從圖中可以看出,球凹/球凸結構為在球凸上方內嵌一個球凹結構。模型總長度為110 mm,壁面厚度為1 mm,進口段和出口段長度各30 mm,30~80 mm處為加熱段,通道橫截面結構為2×2 mm結構。固體壁面選擇為鋼材料,內部流體為超臨界氫。本文邊界條件參考文獻[10]的邊界條件,在實際的再生冷卻通道中,氫氣是從亞臨界狀態過度到超臨界狀態的流動過程,本文僅僅研究氫氣在超臨界下的流動變化,所以進口溫度設為300 K,出口壓力為3 MPa,熱流密度q設置為定值3 MW/m2,另外模型中球凸半徑為定值0.5 mm,高度為0.5 mm,間距sp為1.5 mm。
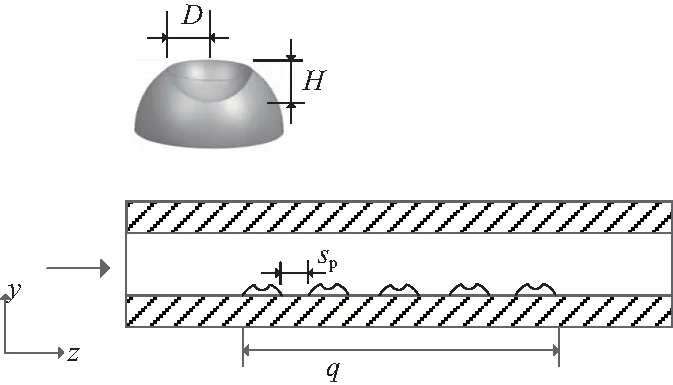
圖3 球凹/球凸結構模型圖
1.4 網格無關性驗證
本文利用ICEM進行網格劃分,在固液交界面加密,設置第一層網格厚度為0.005 mm,共15層網格。選用雷諾數為2.2×104,球凹深度dep為0.3 mm,球凹半徑D為0.4 mm時,對網格量進行驗證。以內嵌擾流結構面上的平均溫度作為參考依據。結果如圖4所示,當網格量>500萬以后,溫度變化僅為1%。綜合考慮計算效率和正確性兩個因素,本文網格采用500萬計算量。
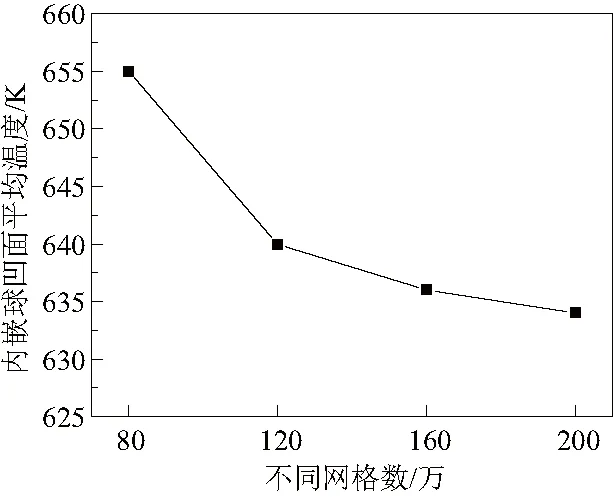
圖4 網格無關性驗證
1.5 參數定義
本文中所涉及的參數如下:
(1)
(2)
(3)
(4)
(5)
其中:h為對流換熱系數;D為通道特征長度;λ為導熱系數;ρ為流體密度;ΔP為通道進出口壓降;L為通道長度;G為通道質量流量;Nu0為光滑通道(無肋)時的努塞爾數;f0為光滑通道(無肋)時摩擦因子。
2 結果分析
2.1 球凹深度對冷卻效果的影響
本研究首先對當球凹半徑為0.4 mm,進口雷諾數Rein為2.2×104時,不同球凹深度對冷卻效果的影響進行了研究,如圖5所示。其中圖中橫坐標0處為無球凹結構。
從圖5中可以看出,綜合換熱因子隨球凹深度呈現先增大后減小的趨勢,在0.3 mm處達到最大值1.40。相比于不加球凹時的1.27,綜合換熱因子增加了0.13。
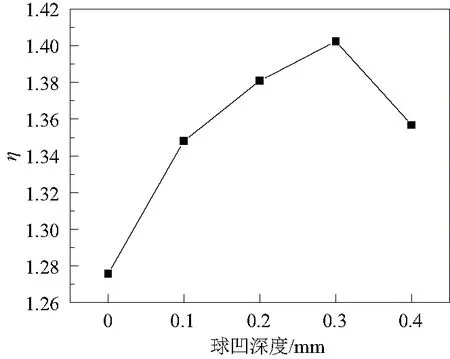
圖5 球凹深度和綜合換熱因子的關系
如圖6所示為流體的流線示意圖,從中可以看出,當球凹深度逐漸增加的時候,首先在球凹內會形成漩渦,加劇了流體之間的混合,增強了換熱效果。
為了研究球凹結構對流體流動的影響,圖7列出了當雷諾數為2.2×104,不同球凹深度在Z=60.5 mm處的流動橫截面的溫度分布圖。
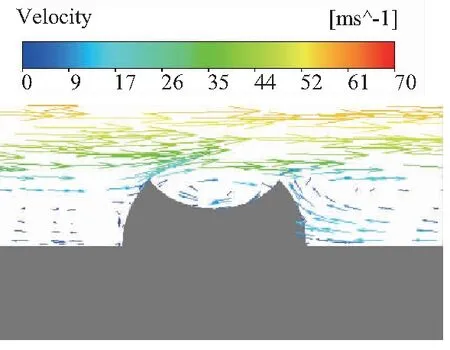
圖6 流體流線圖
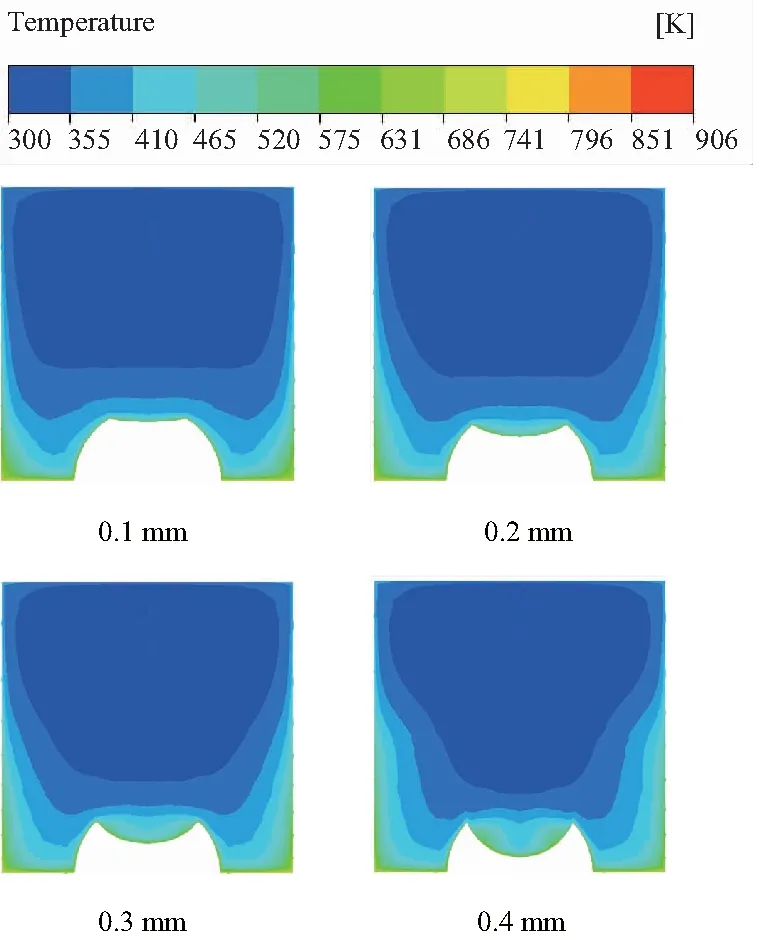
圖7 流體溫度分布隨球凹深度的變化關系
但當球凹深度較深的時候,如圖8所示,在球凹底部會滯留了一小部分高溫流體,且隨著深度增加,滯留的流體越多,高溫流體越會減小流體和高溫固體壁面的溫差,從而導致努塞爾數降低。所以會出現圖8中相對努塞爾數先增大后減小的趨勢。另外球凹深度的增加勢必會帶來摩擦因子的增加,結果如圖9所示。最終使得綜合換熱因子呈現先增大后減小的趨勢。
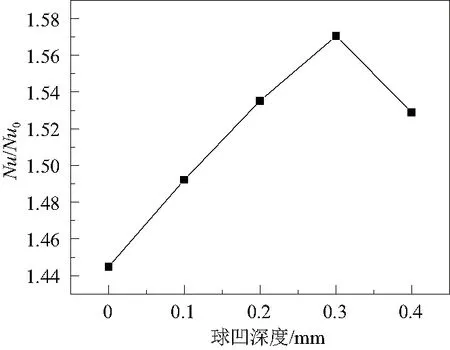
圖8 球凹深度和相對努塞爾數的關系
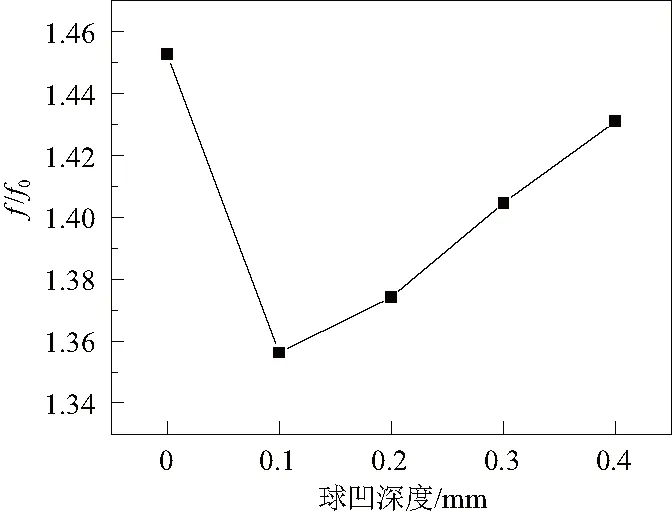
圖9 球凹深度和相對摩擦因子的關系
2.2 球凹半徑對冷卻效果的影響
當球凹深度為0.3 mm,進口雷諾數Rein為2.2×104時,不同球凹半徑對冷卻效果的影響如圖10-圖12所示。其中圖中橫坐標0處為無球凹結構。
首先從圖12可以看出,隨著球凹半徑的增加,綜合換熱因子隨之增加,當球凹半徑從0.3增加到0.6 mm時,綜合因子從1.33增加到1.41。這主要是因為當球凹的存在強化了球凹上方流體的湍流,當球凹半徑增加的時候,球凹所能強化流體的范圍變大,所以導致流體的相對努塞爾數隨球凹半徑的增加而增加,結果如圖10所示。另外,球凹半徑的增加使得流體的通道面積增加,所以使得相對摩擦因子隨著球凹半徑的增加而減小,結果如圖11所示。綜合兩者因素,得到綜合換熱因子隨著球凹半徑的增加而增加。
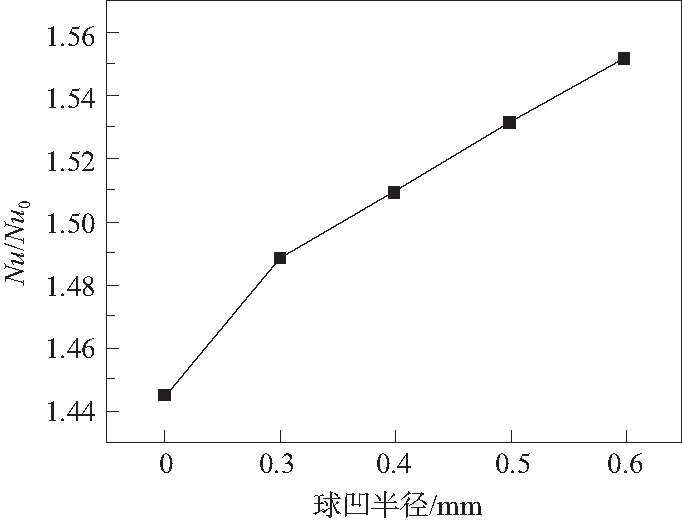
圖10 球凹半徑和相對努塞爾數的關系
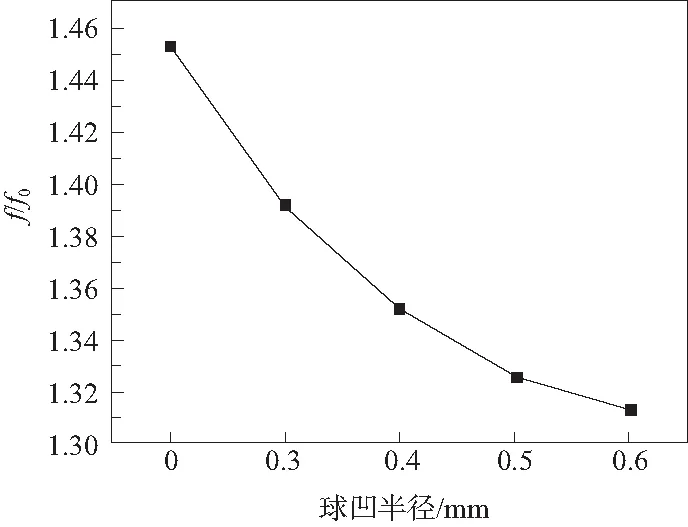
圖11 球凹半徑和相對摩擦因子的關系
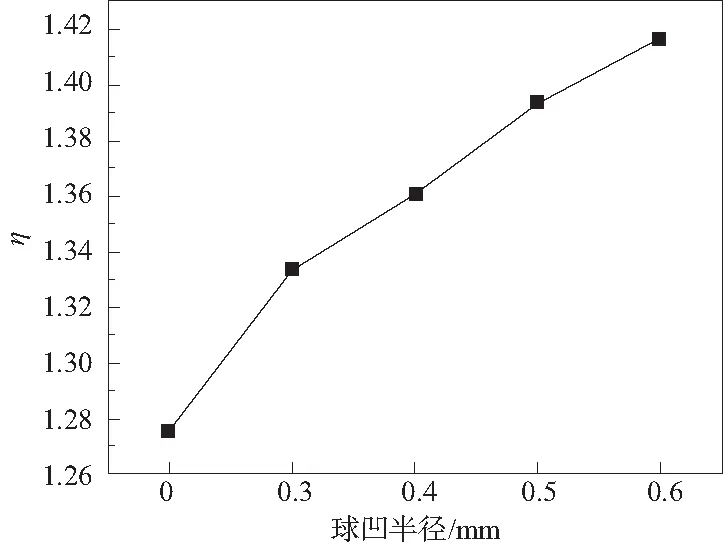
圖12 球凹半徑和綜合換熱因子的關系
3 結語
文中利用Fluent軟件,分析內嵌球凹結構對再生冷卻矩形通道管內超臨界氫燃料的流動影響,所得結論如下:
1) 當球凹深度為0.3 mm時,綜合換熱因子最高,相對于無球凹結構時,綜合換熱因子增加了0.13。
2) 當球凹深度過大時,在球凹底部會滯留小部分高溫流體,影響換熱。
3) 當球凹半徑增加的時候,使得球凹所能強化流體的范圍變大,導致流體的相對努塞爾數增加,另外球凹半徑的增加使流體的通道面積增加,從而減小了相對摩擦因子。

