基于遷移成分分析的跨域軸承故障分類方法研究*

蘭雨濤,胡超凡,金 京,王衍學*

(1.北京建筑大學 機電與車輛工程學院,北京 100044;2.桂林電子科技大學 機電工程學院,廣西 桂林 541004)

0 引 言

目前,滾動軸承的智能故障診斷技術發展迅猛[1-3],能夠快速、高效地對故障進行識別分類。但是智能故障診斷方法存在一個重要的假定,即標記的訓練數據和未標記的測試數據要服從相同的分布[4]5525。然而,該假定存在兩個缺陷:(1)被標記的故障數據很難從一些機器中收集上;(2)用標記的數據訓練的智能故障診斷算法識別未標記的樣本,可能會因為標記和未標記的數據集是從不同機器上獲取的,從而導致失敗[5]。因此,源域和目標域間存在分布差異,并可造成重要的分類性能退化[4]5529-5530。換而言之,發現一個良好的跨域特性表示很關鍵。一個好的特征表示可以盡可能減少域間分布的差異,并能夠保留原始數據的重要屬性。

為了解決域分布問題,域自適應技術被構造出來[6]。域自適應算法通過域不變子空間特征,構造從源域到目標域的知識遷移[4]5526,該算法已經得到了成功的應用[7,8]。在學習域適應的公共特征表示方面,YANG S和ZHANG Y等人[9]基于串行自編碼提出了新的表示學習框架,通過穿行連接兩種不同類型的自動編碼器,提取了更豐富的特征表示。SHEN J和QU Y等人[10]利用一個用于評判標識的神經網絡估計源樣本和目標樣本之間的經驗Wasserstein距離,并通過優化特征提取網絡,以最小化估計Wasserstein距離,進而學習域不變特征表示。ZHAO H和COMBES RTD等人[11]描述了當邊緣標簽分布因源域到目標域不同時,學習不變表示和兩個域上實現小聯合誤差之間的基本權衡。何志海[12]提出了一種對目標域特征分類具有一致性正則的非監督域自適應算法框架,從而提高了源域分類器對目標域特征分類的準確性。

但是,目前這些算法不能推廣到樣本外模式,且無法顯著減小域間分布差異。遷移學習是近年來提出的一種新型機器學習方法,其通過用已獲取的知識作為源域對目標域,或者說相關但有差異的問題進行求解。該算法可以處理難以獲取訓練樣本的學習問題,并且已在文本識別[13]、圖像識別[14]等領域得到初步的應用。

本文提出一種新的特征提取方法,其以遷移成分分析(TCA)算法[15]1187對域自適應算法進行優化;學習源域、目標域下的一組共同遷移成分,以便當投影到當下再生希爾伯特子空間子上時,使不同域的數據分布彼此接近,使源域、目標域的數據分布差異大大減小;基于遷移成分分析的域自適應來直接適應源域和目標域的特征表示,用于解決軸承智能故障診斷中的特征表示適應問題,并對軸承故障進行分類,完成對不同類型的軸承故障的識別。

1 域自適應和TCA理論基礎

1.1 域自適應

由于源域和目標域數據分布不一、存在差異,源域的軸承故障診斷數據不能準確地辨識目標域軸承的未標記數據樣本類別,致使滾動軸承的健康狀態無法正確判斷。

針對上述的域分布差異問題,本文將數據都映射到一個特征子空間中,并在特征子空間中找一個測量準則,使得源域和目標域數據的特征分布盡可能地接近,縮小分布差異。因此,基于源域數據特征訓練出來的判別器,就可以用到目標域數據上,源域軸承的故障診斷知識可以進而辨識目標域軸承的健康狀態。

診斷示意圖如圖1所示。

圖1 故障數據遷移診斷示意圖

基于目標域沒有被標記的訓練數據,但卻有大量未被標記的數據的情況,此處假設:

DS(被標記的數據)在源域中是可用的;DT(未被標記的數據)在目標域中是可用的。

源域數據可以表示為:DS={(xS1,yS1),…,(xSn1,ySn1)}。

其中：xSi∈X—輸入;ySi∈Y—輸出。

目標域數據可以表示為:DT={xTn1,…,yTn1}。

讓P(XS)和Q(XT)(簡寫為P和Q)分別成為XS和XT的邊緣分布;然后,預測與目標域中的輸入xTi對應的標簽yTi。

一個典型的域自適應設置中關鍵假設是:

P≠Q,但P(YS|XS)=P(YT|XT)。

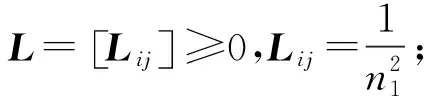
用最大均值差(MMD)作為基于再生核希爾伯特空間(RKHS)的分布比較的相關準則;讓X={x1,…,xn1}和Y={y1,…,yn2}成為分布為P和Q的隨機變量集。

P和Q之間距離的經驗估計可被MMD定義為:

(1)

式中:H—通用的希爾伯特空間,φ:X→H。

因此,兩個樣本分布的距離可以通過兩個樣本映射到一個希爾伯特空間的均值之間的距離,并得到很好的估計。

1.2 遷移成分分析算法

基于:{xSi}—源域中的輸入、{ySi}—源域輸出,{xTi}—目標域中的輸入,預測{yTi}—未知的目標域的輸出。在域自適應中假設邊際密度P(XS)和Q(XT)差異很大,為XS和XT找到一個共同潛在表示,其能保留變換后的兩個域的數據配置。

假設φ是由一個通用核產生的特征映射。如前文所示,兩個分布P和Q間的距離可通過兩個域的經驗均值之間的距離進行測量[15]1188,即:

(2)

因此,最小化這個量可找到期望的非線性映射φ。憑借該方法的作用,式(2)中兩個域的經驗均值之間的距離可以被表示為:

(3)

其中:

(4)

式中:K—(n1+n2)×(n1+n2)核矩陣;KS,S,KT,T,KS,T—分別對應k在源域、目標域、跨域數據上定義的核矩陣。

在轉換設置中,學習核k可以通過學習核矩陣K來解決。由此產生的核矩陣學習問題被表述為一個半定規劃(SDP);然后將主成分分析(PCA)應用于學習核矩陣,去跨域尋找低維隱空間。

筆者提出了一種有效的方法[15]1189:基于核特征提取尋找非線性映射φ,學習核k可以直接推廣到樣本外模式。此外,筆者提出了一種使用明確的低階表示的統一的核學習方法。

一般來說,m?n1+n2,由此可得到核矩陣:

(5)

任意兩個模式xi和xj之間對應的k的核可通過下式得出:

(6)

其中：kx=[k(x1,x),…,k(xn1+n2+x)]T∈(n1+n2)。

(7)

1.3 遷移成分提取

經過式(7)的最小正則化表示,域自適應的核學習問題降至:

s.t.WTKHKW=I

(8)

式中:μ—權衡參數;I∈m×m—單位矩陣;中心矩陣;In1+n2∈(n1+n2)×(n1+n2)—單位矩陣。

其中:I∈n1+n2所有列向量均為1。

通過跟蹤優化問題,式(8)可以重新表述為:

(9)

or

(10)

證明:式(8)的拉格朗日量為:

tr(WT(I+μKLK)W)-tr((WTKHKW-I)Z)

(11)

式中:Z—對稱矩陣。

將式(11)的導數w.r.t設為零,可以得到:

(I+μKLK)W=KHKWZ

(12)

在等式兩邊矩陣的左側各乘以WT,然后將其代入到式(11)獲得式(9)。因為矩陣I+μKLK是非奇異的,得益于正則化項tr(WTW),由此可以得到一個等價跡最大化問題(10)。

式(10)中W的解是對應于(I+μKLK)-1KHK的m個前導特征值的特征向量。因此,所提出的方法即被稱為遷移成分分析(TCA)。

2 軸承故障的跨域特征遷移

本文方法主要由域自適應和TCA算法組成。該方法通過讓源域和目標域樣本在特征子空間上的最大均值差異最小化,從而得到一個降維的特征子空間。源域和目標域間的分布差異在這個子空間內減小,故而實現故障知識的跨域遷移。

具體來說,先獲取滾動軸承的振動信號,將已知工況的滾動軸承振動信號作為源域樣本,未知工況的軸承振動信號作為目標域樣本;利用TCA算法處理源域樣本和目標域樣本的差異性,從而增加源域數據樣本和目標域樣本的相似度;通過最大均值差嵌入的判別可以遷移的源域數據,解決目標域中被標記數據供應不足即實際故障樣本較少的問題,形成基于域自適應的遷移學習軸承故障診斷模型。

由此,源域的軸承故障知識可以用來識別目標域中未知的軸承故障類別。

在軸承故障診斷時,用筆者所提出的方法的診斷流程如圖2所示。

圖2 遷移成分分析故障診斷結構圖

3 實驗驗證與結果分析

3.1 實驗數據

本文研究中的數據集由桂林電子科技大學的MFS試驗臺和凱斯西儲大學(CWRU)提供。

軸承的4種不同健康狀態包括外圈故障(OF)、內圈故障(IF)、滾動故障(BF)和正常(N)狀態。本文研究中含有兩種故障的尺寸大小分別為0.007 in與0.001 4 in。此外,使用的故障振動信號是通過兩種電機負載0 HP、1 HP獲得的。所以,基于本文設定的4種健康狀態,一共有8種軸承工況。

用所提算法對每種不同故障尺寸數據提取特征,以驗證所提出的基于遷移成分分析的域自適應軸承智能故障診斷技術的有效性。a數據訓練b測試;反之,b進行訓練a測試。

實驗的遷移任務包括AB、BA、CD、DC、EF、FE、GH、HG。其中,TAB表示以故障尺寸為0.007 in的滾動體作為源域,以故障尺寸為0.014 in的滾動體作為目標域。反之,TBA則以故障尺寸0.014 in為源域,0.007 in為目標域。

類似地,TCD、TDC、TGH、THG依照相似的模式;其中,TEF、TFE表示正常狀態下0 HP負載和1 HP負載互為源域和目標域。在源域的遷移任務中獲得標記的樣本數據,同時在目標域的每種對應工況下獲得未標記的樣本數據。

在兩種故障尺寸和兩種載荷下,8種提取時域信號后的跨域軸承故障分類任務,如圖3所示。

圖3 4種健康狀態下的跨域故障分類任務

3.2 基于GUET數據集的跨域故障分類結果

在本小節中,將采用GUET數據集來驗證所提出的方法。具體來說,橫向比較的方法包括JDA(joint distribution adaptation)和SVM(support vector machine)。

為了驗證所提出方法的有效性,筆者挑選了遷移任務TAB和TFE進行分析。選擇遷移任務TAB和TFE是因為在此兩項任務中,本文所提出的方法獲得了遠高于其他兩種對比方法的分類效果。

遷移任務TAB預測標簽與實際標簽關系,如圖4所示。

圖4 遷移任務TAB預測標簽與實際標簽關系圖

遷移任務TFE預測標簽與實際標簽關系,如圖5所示。

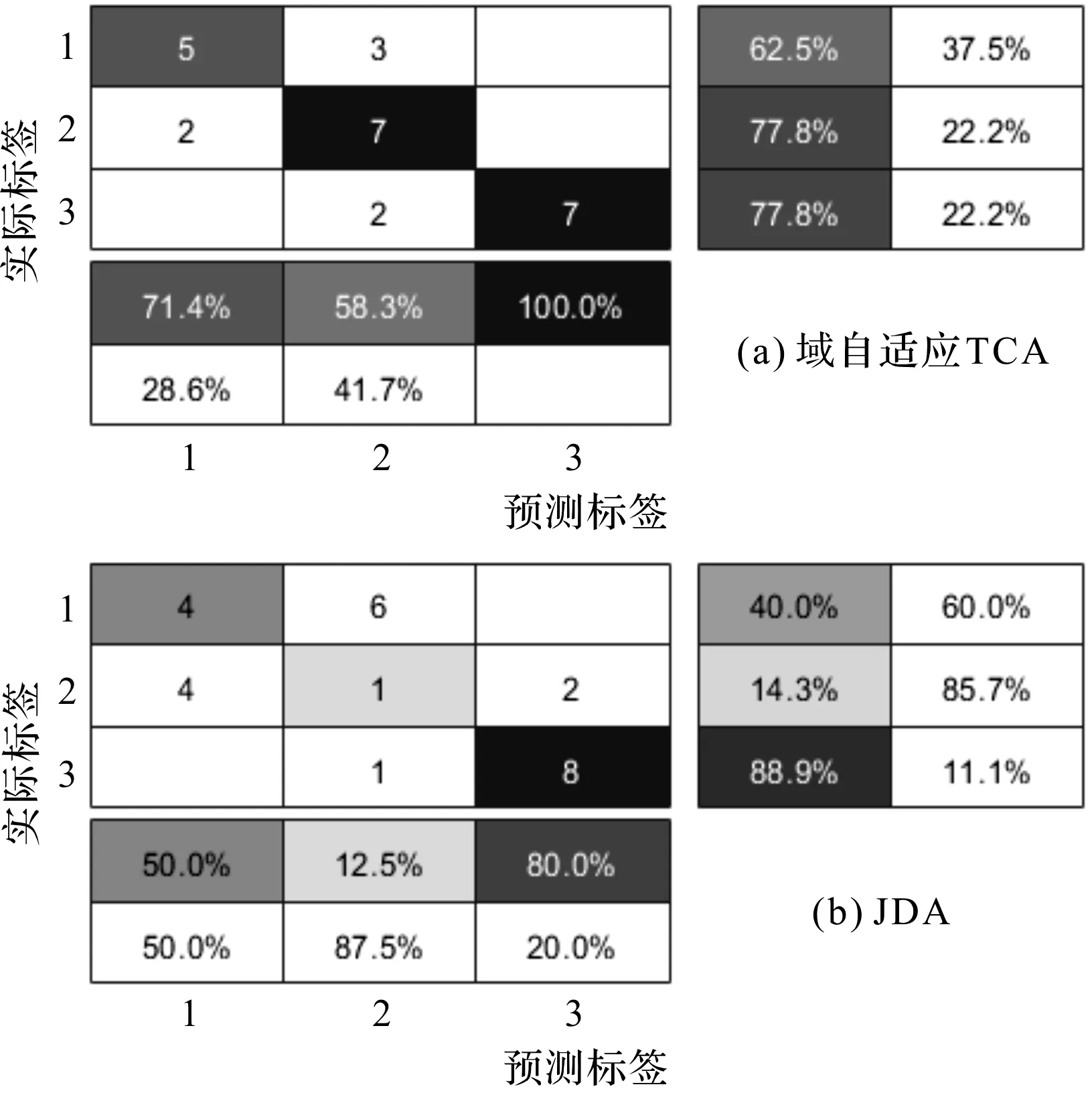
圖5 遷移任務TFE預測標簽與實際標簽關系圖

圖(4,5)中,每個模糊矩陣共有3組數據,每行分別代表滾動體、內圈和外圈數據。橫向為預測標簽的分類,豎向為實際標簽的跨域分類。其中，黑色與灰色為正確分類,白色為錯誤分類。為了直觀對比本文所提方法的分類效果,此處一并列出了其余兩種對比方法的分類模糊矩陣。

從圖4所表示的3種方法下的TAB任務所對應的模糊矩陣可以觀察到:

本文提出的域自適應TCA跨域分類技術的測試準確度能夠達到95.27%,預測標簽的測試精度也達到了94.87%;而JDA的跨域測試精確度只有38.47%,SVM的跨域測試精確度也僅為45.03%;

圖4(a)所代表的本文所提方法的分類精度,無論在實際標簽還是在預測標簽上的測試精確度,都遠遠優于圖4(b,c)中的兩種方法。

本文所提方法,同樣可以在圖5的遷移任務TFE中觀察到如遷移任務TAB同樣優越的分類效果。本文技術的測試準確度可以達到76.57%,而JDA的跨域測試精確度為47.5%,SVM的跨域測試精確度過差只有11.53%;同時,每一組的分類精確度也比對比方法優越。JDA和SVM的精度僅在個別組預測標簽上表現尚可,但是總體平均精度效果稍差。本文提出的分類技術在3種預測和實際標簽的分類精度均優于所列的對比方法。

從圖(4,5)還可以看出:所提出的基于遷移成分分析(TCA)的域自適應方法,不但能夠對經過訓練的滾動軸承樣本跨域特征之間的分布差異進行有效地處理,而且能夠擴大類別之間可遷移特征的距離。

根據圖(4,5)所示的結果表明:提出的方法能比其他方法對跨域遷移任務的目標域進行更有效、更精確的分類,能夠進一步地拓展診斷機械裝備各類故障。

3.3 基于西儲大學(CWRU)數據集的跨域分類結果

為進一步驗證所提方法的有效性,此處筆者采用來自凱斯西儲大學(CWRU)的典型的benchmark跨域對象識別數據集,來驗證筆者所提的方法。

與GUET數據集相同,CWRU含有同樣8種遷移任務,本小節挑選了遷移任務TBA進行分析,如圖6所示。

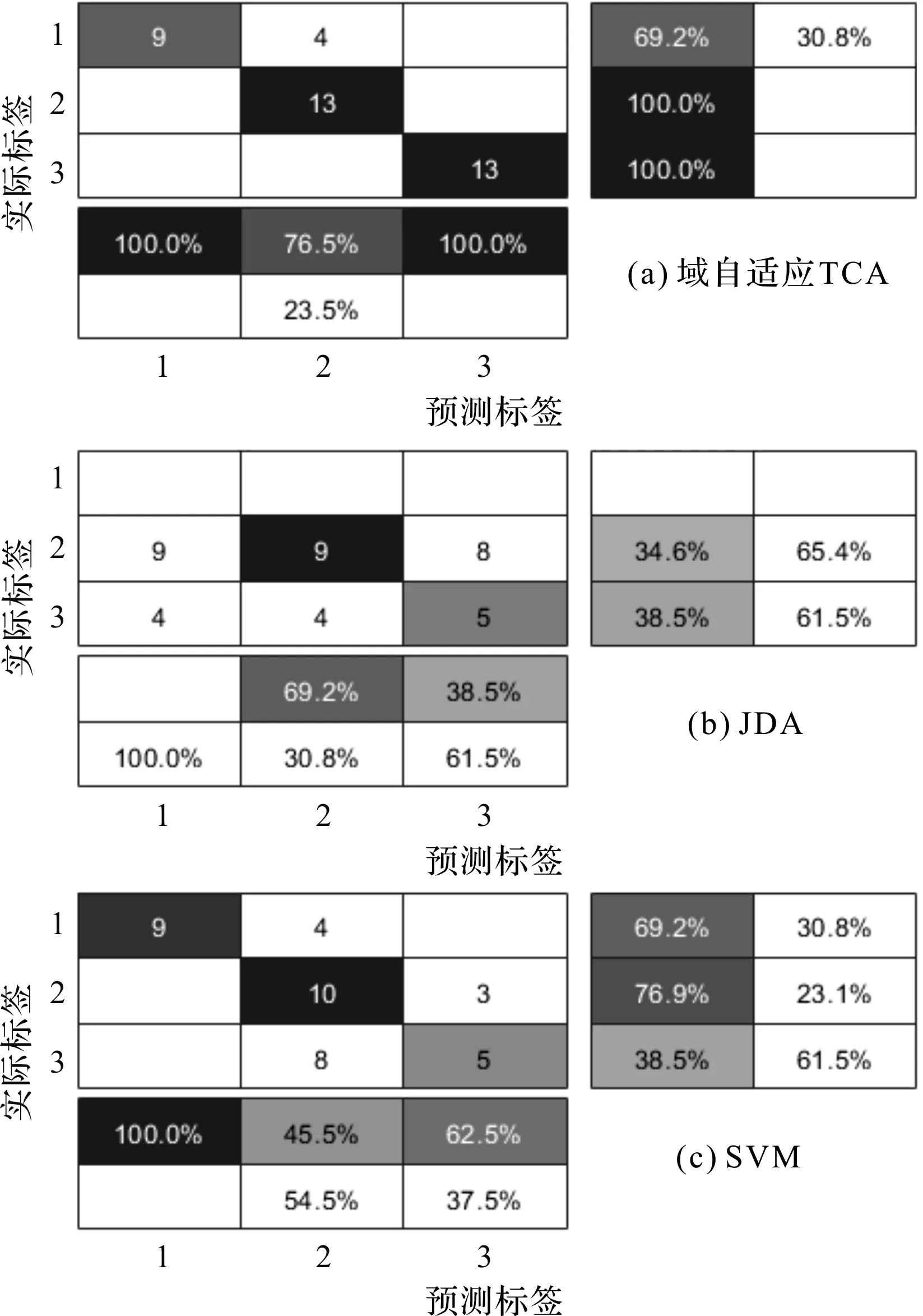
圖6 CWRU遷移任務TBA預測標簽與實際標簽關系圖

圖6中,所提技術的分類準確度為92.17%,同時JDA與SVM的測試精確度僅為35.9%和69.33%。該結果清楚地展示了所提方法比其他方法能夠更精確、有效地對目標域中的遷移任務進行分類,識別故障類別。

筆者使用t-SNE方法進一步對所提方法與對比方法的差異性進行定性分析,將跨域學習過程可視化,提取的故障特征被呈現在二維平面。

遷移任務TBA故障特征分布散點圖如圖7所示。

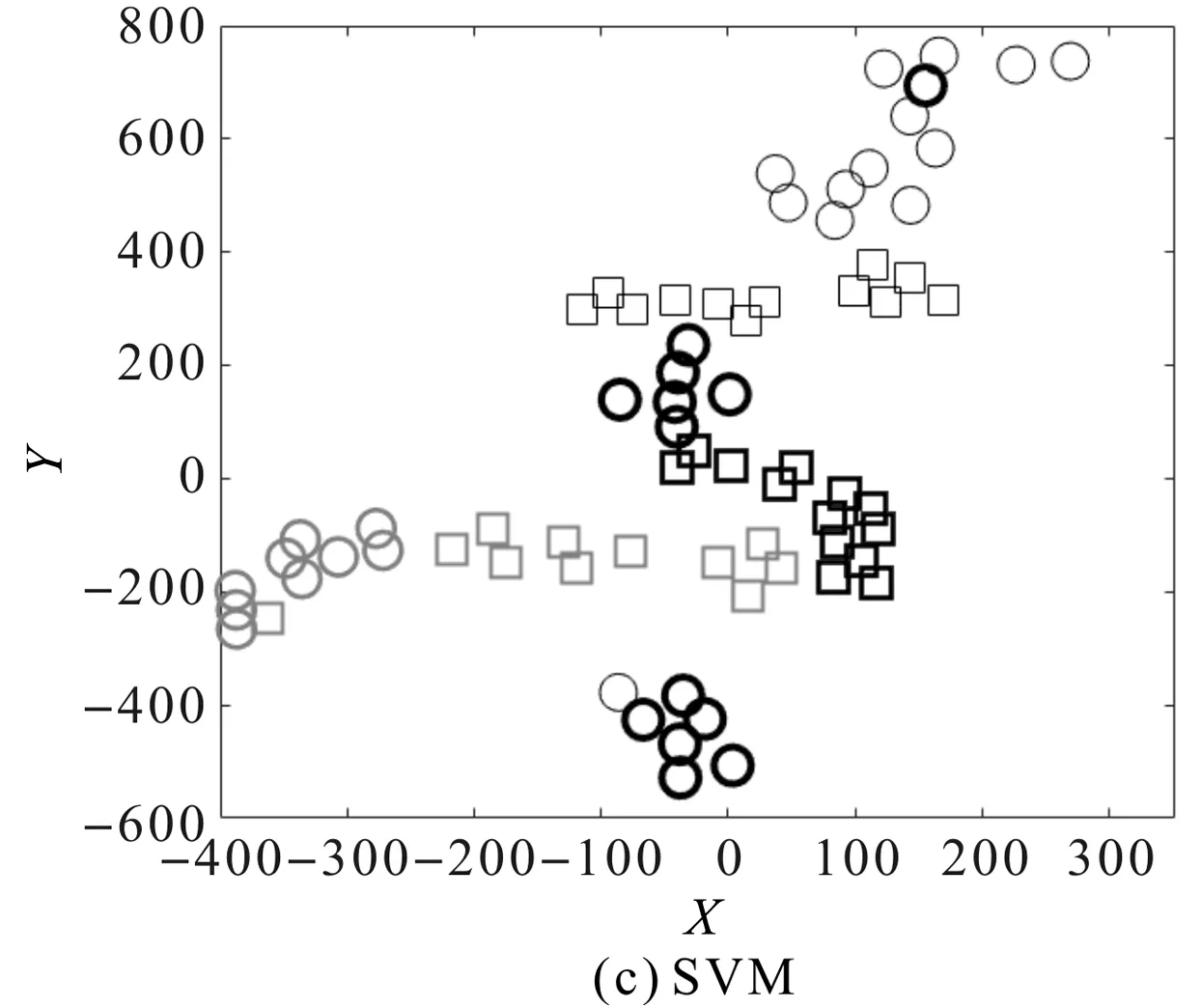
圖7 遷移任務TBA故障特征散點分布圖

從圖7(a)可知:相對于圖7(b,c)所展示的對比方法,本文方法擴大了不同健康類別間可遷移特征的距離,縮小了源域和目標域故障特征的分布差異,減小了測試集和訓練集之間的分布差異對軸承診斷的影響;與圖7(b,c)的對比方法相比,所提方法在將各故障類別有效分離的同時,也將同種工況樣本更好地匯集在一起。

遷移診斷精度對比圖如圖8所示。

圖8 遷移診斷精度對比圖

從圖8不同方法的對比條形圖可看出:本文所提方法擁有最高的分類準確度,是3種故障分類方法中最高的;本文提出方法的跨域分類效果比其余兩種方法更加優越;所提出的方法在8種跨域軸承故障分類任務中均獲得了最高的測試準確度。

該結果主要因為:本方法通過遷移學習能夠將來自源域的樣本數據遷移至目標域中,從而克服了由目標域樣本數據少或難以獲取目標域故障樣本,而造成的故障識別率低的缺陷。

8種遷移學習任務的分類準確度如表1所示。

表1 8種遷移學習任務的分類準確度

(續表)

由表1可以看出3種不同方法分類精確度進行比較的實驗結果:

本文提出方法的平均測試準確度達到了80.85%,而其余兩種對比方法因無法解決嚴重的域分布差異問題,缺乏故障樣本的遷移過程,不能從目標域中提取更好的特征等原因,導致SVM的平均測試準確度為48.31%;而JDA的分類準確度僅僅為46.83%。

通過定量分析可看出:本文方法在每一種故障分類任務中的分類精度均大于兩種對比方法。總的來看,本文通過基于TCA的域自適應方法所實現的分類精度要比其余對比方法優越很多。

4 結束語

本文提出了一種新的基于遷移成分分析的域自適應方法,用于軸承的跨域智能故障診斷,以及在標簽數據難采集或可用數據稀少時,識別旋轉機械裝備的健康狀態。

研究結論如下:

(1)本文方法能夠實現域間,即不同工況下,軸承樣本數據的遷移學習;通過尋找共同成分進行遷移學習,增加域間數據集的相似度,進而解決了測試樣本與訓練樣本需要滿足獨立同分布要求的缺陷;

(2)所采用的方法適應小樣本分類,顯著提升了軸承健康狀態的分類準確度;提出方法的最高分類精度達到95%,平均準確度達到了81%,比常用分類方法的準確類提升了70%左右。

通過與其他診斷方法的對比實驗,驗證了所提出方法的優越性和有效性,能夠高效地辨識軸承的健康狀態,完成對不同類型的軸承故障的識別。