一種脊線提取方法在軸承故障診斷中的應用
陳 劍 楊 斌 黃凱旋 蔡坤奇 劉圓圓 劉幸福
1.合肥工業大學噪聲振動研究所,合肥,2300092.安徽省汽車NVH工程技術研究中心,合肥,230009
0 引言
滾動軸承是旋轉機械的重要組成部件,被廣泛應用于航天、冶金、交通運輸等行業。因工作環境惡劣、載荷變換不定等因素,滾動軸承成為最容易出現故障的部件之一。運轉中的軸承一旦出現故障可能會導致機械損壞,甚至會造成重大的安全事故,因此,對滾動軸承的工作狀態進行監測具有重要的工程意義。
時頻分析方法近年來被廣泛應用于各學科領域的信號分析處理,如地質學[1]、語音[2]、通信[3]、機械工程[4]等。滾動軸承故障振動信號大多是非平穩信號,時頻分析方法在分析該類信號時相比于時域和頻域分析方法更有優勢。鄭近德等[5]提出了一種自適應無參經驗小波變換方法,并將其與希爾伯特變換結合,成功診斷出轉子運轉過程中的局部磨損故障;張尚斌等[6]在研究列車軸承故障診斷中,為解決列車運動所產生的多普勒頻移和擴展問題,提出了一種時頻幅值匹配的多普勒校正方法;丁夏完等[7]針對傳統短時傅里葉變換(STFT)帶寬固定問題,提出了一種以三階B樣條函數作為窗函數的自適應STFT,并應用于滾動軸承的故障診斷,取得了良好的效果。時頻分析方法提供了時域和頻域的聯合分布信息,可以獲取信號的瞬時頻率特征。關于瞬時頻率的提取方法,徐曉迪等[8]將時頻譜在時頻平面上進行壓縮重排,從而提取頻譜上的能量脊線,克服了脊線提取不完整的缺點;王超等[9]通過小波系數的局部模極大值初步提取小波脊,并施加罰函數來平滑小波脊的不連續性,最后采用動態規劃的方法得到了新的小波脊;汪曉珊等[10]提出了一種頻譜集中性指標,通過粒子群優化算法找到該指標的最優值,進而估計對應的初始頻率參數。
雖然很多學者對瞬時頻率的估計方法做了大量研究,取得了不少研究成果,但是瞬時頻率的提取依然存在很多困難,例如信號中干擾噪聲能量較大時瞬時頻率提取的準確率難以保證,提取過程中需要對信號進行各種繁瑣的處理,不能同時提取多個不同的特征頻率等。針對以上問題,本文提出一種改進的Crazy Climber算法,在一定程度的強噪聲干擾情況下,實現了多個瞬時頻率的同時提取,提高了瞬時頻率提取的準確性。
1 基本原理
1.1 短時傅里葉變換
STFT的基本思想是使用窗函數截斷分析信號,使其被分為多個片段信號,將這一系列片段信號視為平穩信號并分別進行傅里葉變換,從而得到不同頻率分量在時域上的變化情況。定義為

(1)
式中,x(τ)為分析信號;g(τ-t)為窗函數;g*表示共軛;F(t,f)為分析信號在時刻t的頻譜。
對于離散數字信號,其離散的STFT為
(2)
式中,g(k)為窗函數的離散形式;m為離散后的時間段;F(m,f)為一個二維的復矩陣,行對應采樣時間點,列對應頻率值。
對F(m,f)求模得到時頻幅值矩陣:
S(m,f)=|F(m,f)|
(3)
STFT常使用的窗函數有Hamming窗、Hanning窗、Gaussian窗和Blackman窗,本文在對信號進行STFT時采用的是Blackman窗。
1.2 脊線提取算法
1.2.1 Crazy Climber算法
時頻分析過程中,時頻脊線的提取對確定某一時刻的頻率信息尤為重要,目前的脊線提取方法對多源脊線的提取較為困難,且信號中的噪聲干擾較大時,時頻脊線提取效果不佳。針對此問題,CARMONA等[11]提出一種Crazy Climber算法,實現了多源脊線同時提取。該算法將一系列按一定規則運動的點(Climber)視為密度分布,所有點按照相同的規則在平面上運動,并逐漸被脊線位置所吸引,從而聚集在脊線位置上,使得Climber對脊線位置的訪問次數遠遠高于其他位置,通過對各位置訪問次數進行統計獲得度量矩陣,再對度量矩陣進行局部最優峰值提取,并將度量值較高的位置連接起來即可獲得脊線。采用Crazy Climber算法提取脊線的過程包含度量矩陣獲取和局部最優峰值提取兩個過程。
若信號的時頻矩陣S為M×N矩陣,則使用Crazy Climber算法對其進行脊線提取的具體步驟如下。
(1)初始化K個Climber、度量矩陣D、觀測矩陣R以及Climber移動次數n。K個Climber均布在與時頻矩陣S維度相同的觀測矩陣R中,D初始化為與S維度相同的零矩陣。
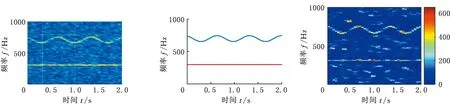
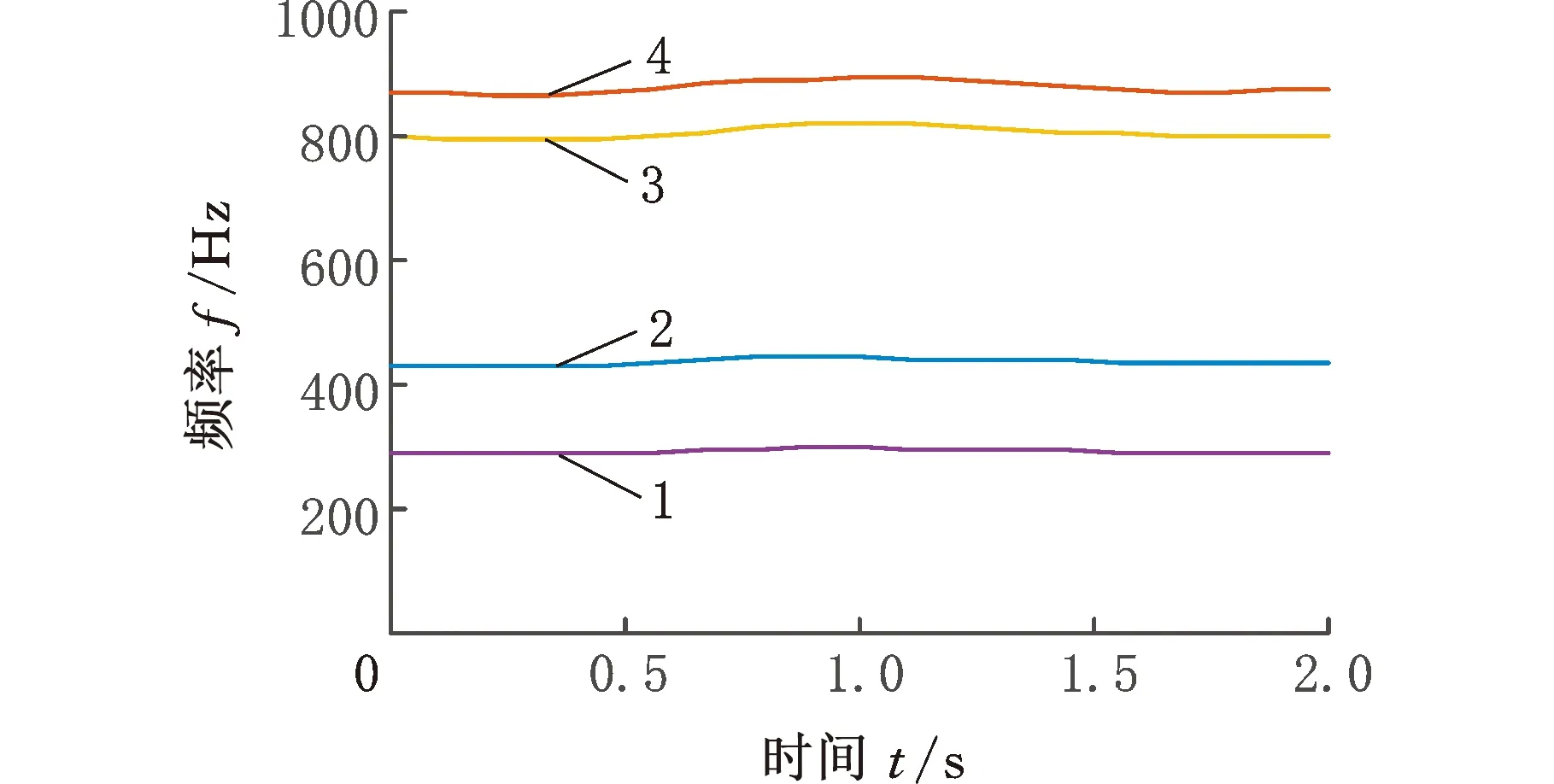
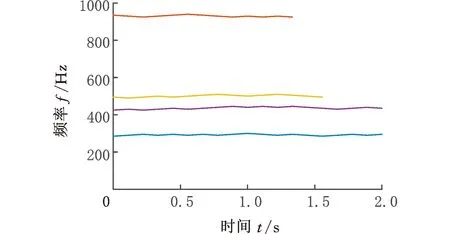
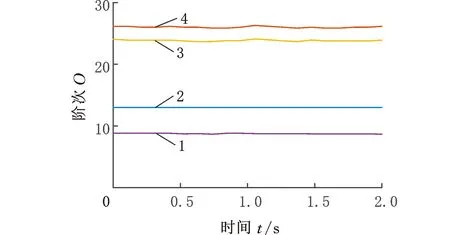
(2)Climber每次移動對應的時間用tk(k=1,2,…,n)表示,若tk時刻Climber的位置R(tk)=(i,j),則tk+1時刻Climber的位置R(tk+1)=(i′,j′)由以下規則確定:①Climber進行水平方向上的移動,若Climber在R內部(2≤j≤N-1),則tk時刻,Climber以1/2的概率左移或右移一列,即j′=j-1或j′=j+1;若Climber在R邊界處(j=1或j=N),j=1時,j′=2,即Climber在左側邊界時,直接向右移動一列,j=N時,j′=N-1,即Climber在右側邊界時,直接向左移動一列。②水平方向的移動完成后,進行豎直方向的移動,該方向的移動規則與水平方向不同,首先以相同的概率上移一行(i″=i-1)或下移一行(i″=i+1):若S(i″,j′)>S(i,j′),則i′=i″;若S(i″,j′) pk=exp((S(i″,j′)-S(i,j′))/Tk) (4) Tk=(max(S)-min(S))/(lbk) (5) (3)移動完成后,在度量矩陣D的相應位置上增加度量值1,即Dk+1(i′,j′)=Dk(i′,j′)+1。 (4)重復步驟(2)、步驟(3),直到移動次數達到設定值,迭代結束,獲得整個度量矩陣Dn。 (5)對度量矩陣Dn在時間方向進行遞歸,給定任一點(i,j),在(i,j+1)和(i±1,j+1)里尋找最優的相鄰點,并與之形成一條脊線。 (6)重復步驟(5),直到所有滿足要求的點都在脊線中,形成整個時頻面的脊線。 (7)計算每條脊線的長度,設定長度閾值,剔除長度小于閾值的脊線,剩下的脊線即為提取的時頻脊線。 需要說明的是,在進行第(5)步之前,考慮到噪聲影響,需要設定一個閾值e用于將脊線從Dn的低度量值中區分出來: (6) e一般為整個度量矩陣度量均值的倍數或最大度量值的小數倍。 上述脊線提取過程中,步驟(1)~步驟(4)為度量矩陣獲取過程,步驟(5)~步驟(7)為提取局部最優峰值獲取時頻脊線過程。 1.2.2改進的Crazy Climber算法 Crazy Climber算法雖然能夠實現多條脊線同時提取,但是依然存在許多不足之處。首先,在度量矩陣獲取過程中,效率不高,即需要經過很多次迭代才能使脊線位置的度量值與其他位置的度量值有明顯的區分,主要原因是Climber水平方向的移動具有隨機性,豎直方向上的移動雖然有規定的準則,但是隨機性也比較強,同時,當Climber位于矩陣邊界時,只能反方向移動,這使得該Climber又重復移向已經移動過的位置,導致其遍歷全部位置的速度較慢,無法快速準確地向脊線位置移動。其次,在局部峰值提取獲得脊線的過程中,獲取的脊線不夠平滑、準確,導致無法正確提取瞬時頻率。為了解決以上兩個問題,本文提出了改進的Crazy Climber算法。 (1)針對度量矩陣獲取效率低的問題,提出改變Climber在時頻空間的移動規則,使其能夠更加快速地向脊線位置移動。若tk時刻Climber對應的位置R(tk)=(i,j),則tk+1時刻Climber對應的位置R(tk+1)=(i′,j′)確定規則如下。 Climber以一定的概率向相鄰的6個位置移動,這6個位置用Au(u=1,2,…,6)表示,見圖1,移動到Au的概率pu由時頻矩陣中Au位置對應的頻率幅值相對于R(tk)位置的頻率幅值的增量ΔAu決定: (a)非邊界Climber可移動位置 (7) 增量越大,移向該位置的概率也越大。為避免ΔAu出現負值,進行如下處理: ΔA′u=ΔAu+|min(S(Au))-S(R(tk))| (8) Climber移動到Au的概率 (9) ①當R(tk)位于矩陣內部時(2≤i≤M-1且2≤j≤N-1),則tk+1時刻Climber可能移向的6個位置如圖1a所示。此時Au對應于時頻矩陣中的坐標為A1(i-1,j-1)、A2(i,j-1)、A3(i+1,j-1)、A4(i-1,j+1)、A5(i,j+1)、A6(i+1,j+1)。 ②當R(tk)位于矩陣邊界時,則tk+1時刻Climber可能移向的6個位置如圖1b所示。對時頻分布矩陣進行首尾對應相接,得到相應的Au點視為tk+1時刻Climber可能移向的位置。此時,圖中Au對應于時頻矩陣中的坐標為A1(i-1,j-1)、A2(i,j-1)、A3(1,j-1)、A4(i-1,j+1)、A5(i,j+1)、A6(1,j+1)。 需要說明的是,圖1b中只是R(tk)在矩陣邊界上的一種情況,其他情況下,Au的位置變換與此種情況類似。 Climber按照以上的規則進行移動,能夠確保其移動趨勢方向始終朝著脊線方向,同時當Climber移向矩陣邊界處后無需返回,使其能夠更加快速地對全部位置進行度量,極大地提高了度量矩陣的獲取效率和質量。 (2)針對局部峰值提取脊線的過程中,提取的脊線不夠平滑、準確這一問題,對原有的局部峰值提取方法進行改進,通過多點共同決定局部峰值點的位置來提高脊線的準確性和平順性。 旋轉機械工作過程中,轉動部件對應的頻率與機械轉速有關,由于轉速變化是連續變化過程,這就使得時頻圖中轉動部件對應的頻率是光滑連續的曲線。 如圖2a所示,設w為時頻圖中一條脊線,F、G、H為w上三個相鄰的點,F為t-1時刻點,G為t時刻點,H為t+1時刻點,在對H點位置進行確定時,其位置應在點G的斜率方向附近,如圖2b所示,F、G兩點之間的連線方向為點G的斜率方向,指向t+1時刻的H2點,H1和H3為H2在豎直方向附近的點,那么H點的位置可認為是H1、H2、H3中最大值對應的位置。將此方法用于度量矩陣的局部最優峰值提取,具體提取方法如下:對于時頻圖中的某一條脊線,t-1時刻和t時刻該脊線對應于度量矩陣中的位置分別為Et-1(it-1,jt-1)、Et(it,jt),則t+1時刻的位置應為(2it-it-1,jt+1)和(2it-it-1±1,jt+1)中最大度量值對應的位置。另外,當t時刻是開始時刻時,由于此時t-1時刻不存在,則t+1時刻的位置為(it,jt+1)和(it±1,jt+1)中最大度量值位置。 (a)脊線圖 (b)局部峰值提取圖圖2 局部最優峰值提取示意圖Fig.2 Diagram of local optimal peak extraction 可以看出,該方法在進行局部最優點選取時,局部最優點由前兩個局部最優點的位置共同決定,提高了提取脊線的平順性和準確性。 階次分析是分析旋轉機械運動部件故障的一項重要技術。階次是旋轉部件因旋轉造成的振動響應,它獨立于部件的實際轉速,是參考軸轉頻的倍數或分數。如滾動軸承由內圈、外圈、滾動體、保持架四個部分組成,這四個部分發生故障時對應的階次分別為Oi、Oo、Oe、Oc,則 (10) (11) (12) (13) 式中,Z為滾動體的個數;d為滾動體的直徑mm;D為軸承的節徑,mm;α為接觸角。 為驗證改進的Crazy Climber算法在時頻分析中的有效性,構造含有白噪聲的仿真信號x(t): (14) 其瞬時頻率為 (15) 該仿真信號的采樣頻率fs=10 240 Hz,式中,t=[0∶1/fs∶2],η(t)為信噪比為1dB的高斯白噪聲。x(t)時域波形如圖3所示。 對仿真信號進行短時傅里葉變換,得到時頻矩陣,分別使用改進的Crazy Climber算法和原始Crazy Climber算法對時頻矩陣進行脊線提取,兩種算法中Climber移動次數設為100,度量矩陣度量值的閾值為最大度量值的0.1倍,脊線長度閾值為時頻矩陣寬度的0.5倍。仿真信號脊線提取如圖4所示。 (a)時頻圖 (b)實際頻率脊線圖(c) 改進Crazy Climber算法獲得的度量矩陣圖 從圖4c中可以看出,度量矩陣圖中脊線位置處的度量值遠遠高于其他位置,而圖4d中頻率f2的脊線位置度量值較高,但是頻率f1的脊線位置度量值與非脊線位置的度量值區分度不大,導致其不能被明顯地區分。對圖4c、圖4d的度量值進行分析,可以看出圖4c中脊線處的最大度量值超過了600,而圖4d中脊線處的最大度量值小于200,因此在相同的移動次數下,改進的Crazy Climber算法獲得度量矩陣的質量更高,提高了識別脊線的能力。當原始算法的移動次數設定為230時,可以獲得最大度量值與圖4c相當的度量矩陣,即當改進算法與原始算法的移動次數分別設定為100和230時,兩者獲得的度量矩陣質量大致相同,在此條件下,對兩種算法所需要的時間進行統計。為確保結果的可靠性,每種算法分別進行10次試驗,各次試驗的結果取平均作為最終結果,結果如表1所示,可以看出改進算法需要的時間為0.94 s,原始算法需要的時間為1.18 s,因此獲得相同質量的度量矩陣,原始算法消耗的時間更長。 表1 兩種方法消耗時間對比表 (16) 式中,a為提取脊線的長度;Yr為提取脊線的第r個頻率值;yr為實際脊線的第r個頻率值。 綜上分析,相比于原始Crazy Climber算法,改進的Crazy Climber算法不僅具有更強的脊線識別能力,而且提取脊線的準確性和完整性也可以得到保證。 為驗證改進的Crazy Climber算法在軸承故障診斷中的有效性,對一外圈故障的圓柱滾子軸承進行試驗,軸承上的故障特征通過線切割制造,試驗臺總體結構見圖5,試驗軸承為NSK 公司的NU1010型圓柱滾子軸承,通過加速度傳感器和信號采集系統實現軸承振動信號的采集。試驗過程中,軸承轉速為2000 r/min,采樣頻率fs=20 480 Hz。表2所示為試驗軸承的相關參數,表3所示為該軸承各零件的故障特征階次。 圖5 試驗臺總體結構Fig.5 Structure of the test bench 表2 軸承相關參數 表3 軸承故障階次 從采集的數據中抽取40 960個樣本點,然后使用STFT進行時頻變換,獲得時頻矩陣,圖6所示為時頻圖譜(為方便分析,只對1000 Hz以內的頻率進行顯示);然后使用改進的Crazy Climber算法對時頻矩陣進行脊線提取,提取過程中Climber移動次數設為300,度量矩陣度量值的閾值為最大度量值的0.1倍,脊線長度閾值為時頻矩陣寬度的0.5倍,結果如圖7所示,可以看出,時頻圖中明顯的脊線被完整地提取出來。可以發現,在0.5~1.5 s這段時間,各條脊線對應的頻率發生了變化,使得脊線向上凸起,這是試驗過程中電機轉速不穩定導致的瞬時頻率波動現象。 圖6 故障信號時頻圖Fig.6 Time-frequency spectrum of fault signal 圖7 改進Crazy Climber算法脊線提取結果Fig.7 Ridge extraction result of improved CrazyClimber algorithm 為驗證該改進算法的效果,將其與原始Crazy Climber算法進行對比,使用原始算法對故障信號進行脊線提取過程中,各參數與改進算法脊線提取過程的參數設置相同,其提取結果如圖8所示,可以看出,部分脊線提取不完整,且脊線不夠平順,與時頻圖中的真實脊線差距較大。 因此,改進的Crazy Climber算法總體上優于原始Crazy Climber算法。 圖8 原始Crazy Climber算法脊線提取結果Fig.8 Ridge extraction result of original CrazyClimber algorithm 為實現軸承的故障診斷,對各脊線對應的階次進行提取,由于時頻圖中沒有出現明顯的基頻脊線,所以提取的脊線中也不包含對應基頻的脊線。在該試驗工況下,軸承的基頻為fr=33.3 Hz,分析提取的脊線發現,第2條脊線的頻率對應于基頻的13倍頻,即f2=13fr,因此,可以用第2條脊線各時刻頻率的1/13來代替整個過程中基頻各時刻的頻率,所以fr=f2/13,將各脊線與fr作商即得到對應的階次,結果如圖9所示。計算各脊線階次的平均值,結果如表4所示,可以看出,第2、3、4條脊線對應的都是基頻的整倍頻,第1條脊線的階次與軸承外圈故障階次接近,可以判斷該軸承外圈出現故障,診斷結果與實際相符,證明本文提出的改進Crazy Climber算法在實際應用中可以有效識別軸承故障。 圖9 故障信號特征頻率對應階次Fig.9 Corresponding orders of fault signal 表4 各脊線對應階次 (1)針對Crazy Climber算法度量矩陣提取效率低的問題,提出一種有效的Climber移動規則,實現了度量矩陣快速準確的獲取,提高了脊線提取的完整性。 (2)對Crazy Climber算法中局部最優峰值的提取方法進行改進,提高了提取脊線的準確性。 (3)將改進的Crazy Climber算法應用于軸承的故障診斷中,通過階次分析可準確地判斷軸承的故障類型。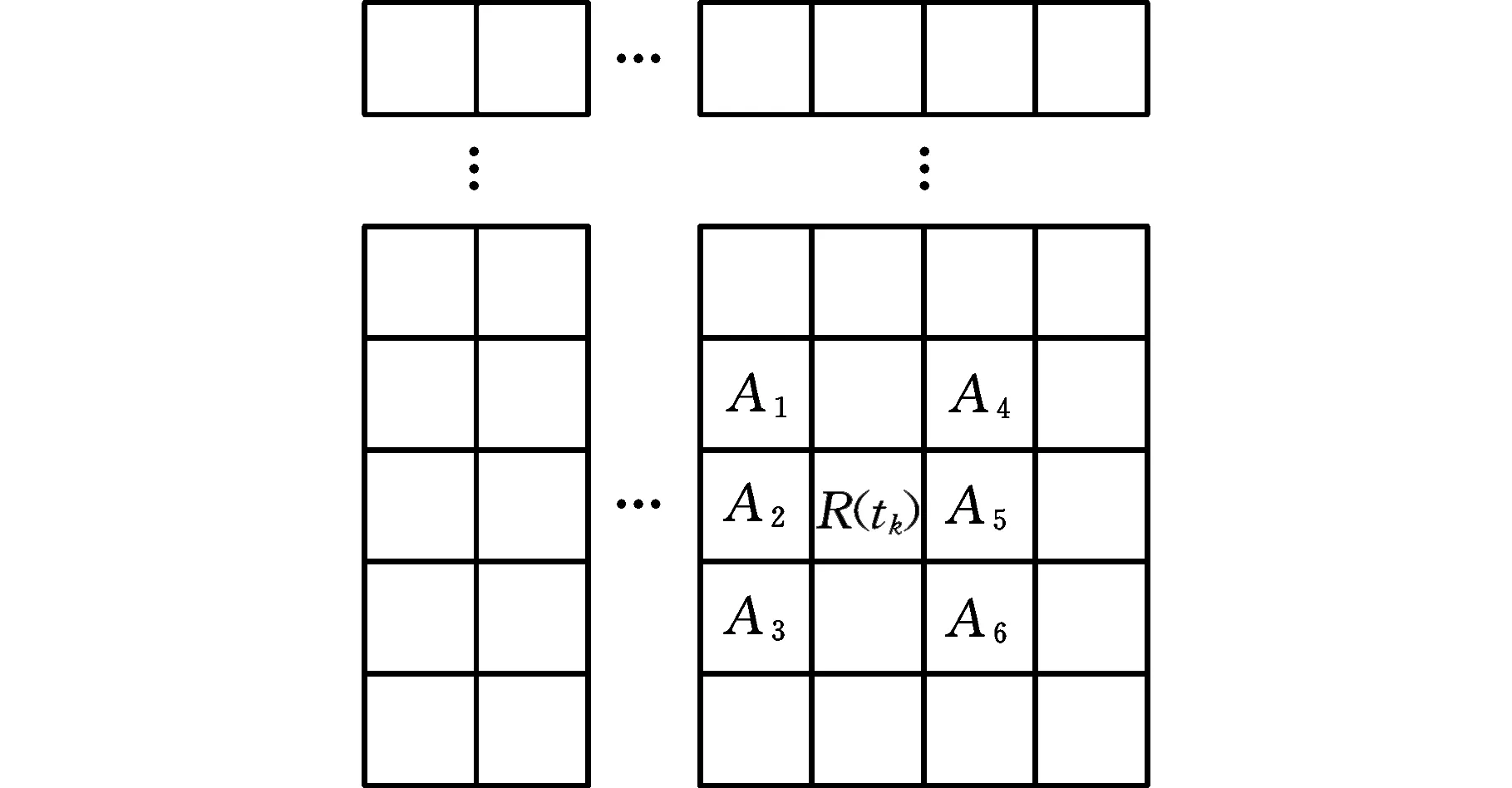

1.3 階次分析
2 仿真信號分析
2.1 仿真信號構造
2.2 脊線提取


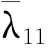
3 試驗分析





4 結論

