求解資源受限多項目調度的改進遺傳規劃算法

陳浩杰 丁國富 張 劍 閻開印

西南交通大學機械工程學院先進設計與制造技術研究所，成都，610031

0 引言

資源受限項目調度問題(resource constrained project scheduling problem , RCPSP)[1-2]是項目管理中最為經典和核心的NP難問題[3]，但RCPSP并不完全適用于眾多復雜實際場景，故需要進行不同方面的擴展，如多技能RCPSP優化[4]、多模式RCPSP優化[5]等，其中資源受限多項目調度問題(resource constrained multi-project scheduling problem, RCMPSP)是應用最廣泛的擴展模式[6-8]，項目管理中約90%是在多項目下進行的[9]。

近年來，RCMPSP的求解方式主要以元啟發式(如進化智能算法)和啟發式(如優先級規則)為主。在元啟發式的研究中，XIN等[10]提出了一種遺傳算法，其編碼方式基于活動優先級且在搜索過程中結合存儲鄰接矩陣，從而提高了搜索能力且避免產生非法解修復過程。ZHENG等[11]設計了一種多智能體架構，并結合關鍵鏈技術以求解分布式RCMPSP。TIAN等[12]通過研究單項目、多項目和活動等三個層次的資源流特性，提出了一種適用于求解RCMPSP的改進關鍵鏈技術。PREZ等[13]提出了一種求解RCMPSP的多模態遺傳算法，通過擴展搜索過程中的種群多樣性來避免算法陷入局部最優。

大量研究表明，PR調度具備快速響應能力和良好的求解能力，但不同的PR具備不同的特性導致其適用的目標函數和場景不同，且PR本身不具備優化能力，因此考慮根據不同PR的優勢去構造適用更廣、求解能力更強的PR。于是超啟發式的理念被提出和逐步應用[19]。

遺傳算法是具備很強通用性和優化能力的元啟發式算法，其優化過程被模擬到超啟發式算法上形成遺傳規劃算法(genetic programing，GP)和基因表達式編程(gene expression programming，GEP)。GP和GEP的進化過程相似，主要區別在于個體的編碼方法和結果的表達[20]。在調度領域，GEP的應用主要集中在作業車間調度(job shop scheduling，JSP)[21-22]。針對項目調度，JIA等[23]提出了一種求解RCPSP的GEP框架。相比而言，GP在項目調度中的應用更廣泛。CHAND等[24]將GP運用到RCPSP求解并成功進化出了調度求解能力更強的PR。在此基礎上，CHAND等[25]考慮了資源擾動下的RCPSP，再次驗證了遺傳規劃的有效性和適應能力。LIN等[26]設計了一種雙層超啟發式遺傳規劃算法求解多技能RCPSP，通過高層的超啟發式算法搜索更好的低層啟發式算法。

綜上所述，現有研究已經成功將GP運用于RCPSP，但據文獻調研并未發現GP在RCMPSP問題上的應用。相較于RCPSP，RCMPSP具備項目層的優先級屬性，且由于不同項目之間的資源搶占和沖突會導致資源需求方面的屬性選取受到影響，GP的有效性需要進一步驗證；同時，現有RCPSP超啟發式調度的研究均是優化單目標，而實際場景中多目標優化的目標間競爭關系會為優化帶來額外困難[27]，并且超啟發式編碼的特性使傳統GP在搜索過程中容易陷入局部最優。基于此，本文提出一種應用于多目標RCMPSP問題的改進遺傳規劃(improved genetic programing，IGP)算法。

1 問題描述

RCMPSP是調度由n個項目組成的項目集P={1,2,…,n}來滿足某個/些目標最優，其中每個項目i∈P都由z+2個具備有向無循環邏輯關系的活動Ai={ai0,ai1,…,ai(z+1)}構成，其中活動ai0和ai(z+1)為虛擬活動，表示項目i的開始和結束。在n個項目的執行過程中，共需要K種共用可更新資源，每種資源k(k∈K)的最大單位供應量為Rk，且設定在執行中的任意時刻t處于執行的活動集合為Et。對于任意活動aij∈Ai,j={0,1,…,z+1}，sij為開始時間，dij為持續時間，Sij為緊后活動集合，rijk為活動aij對資源k的需求量。衡量RCMPSP的調度優劣通常是依據完工時間[14-16]，根據文獻[15]采用兩個目標函數值分別從項目和項目集兩個角度進行PR的性能評估——平均項目完工時間偏差Q1和項目集完工時間偏差Q2。設項目i的關鍵路徑長度為Li，實際調度后所得到的完工時間為Ci，RCMPSP的數學模型如下：

min(Q1,Q2)

(1)

(2)

(3)

s.t.

sib-sij≥dij

(4)

di0,di(z+1)=0ri0k,ri(z+1)k=0

(5)

(6)

i∈Pb∈Sijj∈Aik∈Kt∈{0,1,…}

其中，式(4)表明項目內部各活動的緊前緊后關系，即活動必須在其所有緊前活動完成后才能開始；式(5)為虛擬活動約束，即所有虛擬活動都不需要任何資源且持續時間為0；式(6)為資源約束，即在任意時刻，處于執行狀態的活動所需資源之和不得超過該類資源的最大供應量。目標函數式(1)表示采用非支配解的方式優化評估，如下所示：

(7)

式中，z1、z2表示兩個不同的求解策略。

當式(7)中的不等式至少有一個嚴格小于時，稱z1支配z2，記z1?z2。若策略z不受到其他任何策略的支配，則z是非支配解。本文的優化目標是優化生成一組應用于RCMPSP的非支配混合優先級規則(hybrid priority rule, HPR)，HPR構成的集合稱為Pareto解集(非支配解集)。

2 求解RCMPSP的IGP

WANG等[15]認為，不同PR求解多目標下的RCMPSP，Q1目標最優的PR是最小項目及活動持續時間之和規則，Q2目標最優的PR是最大緊后總數規則，而BROWNING等[14]認為，在不同的問題約束或驗證算例下，調度RCMPSP最好的PR往往不同。可以看出，單一的PR調度時存在一定的局限性，因此需要通過訓練生成適合求解RCMPSP的調度性能優、通用性強的PR。為進化出求解RCMPSP的更優PR，本文提出了一種IGP算法，其流程如圖1所示，收集多種不同工況數據并將其分為訓練集和測試集，通過IGP訓練后得到Pareto解集，再將Pareto解集的各PR在訓練集和測試集上驗證。

圖1 IGP流程圖Fig.1 Flow chart of IGP

2.1 編碼設計及初始化種群

不同于啟發式或元啟發式算法直接得到問題的解，基于超啟發式算法的IGP是為了得到求解問題的進化/混合PR。IGP基因是通過各種優先級屬性經過一定的功能運算符組合后得到的，為了應用于RCMPSP求解，首先需要建立優先級屬性集。在項目調度中優先選擇哪個活動主要是根據活動本身的時間、活動的資源需求和活動在項目中的邏輯關系。在RCPSP中只需要考慮活動層面和資源層面的屬性計算即可，而RCMPSP則需要在多個項目的不同活動之間做出決策，因此需要考慮項目層的屬性。通過分析現有的20種PR[14-16]可知，項目關鍵路徑長度在多項目調度中是主要決策依據，因此本文在RCPSP超啟發式屬性集[24]上增加了項目關鍵路徑長度，從資源、活動和項目的角度提取了10個優先級屬性，并對屬性進行歸一化處理，如表1所示。在RCMPSP中需要在同一時刻決策來自多個項目的活動，因此活動時間相關屬性及關鍵路徑長度采用最大最小歸一化方式；各個活動的邏輯關系只與本項目有關，在衡量活動重要程度歸一化(如Nts和Ntcs)時只考慮與本項目活動總數的比值；不同項目之間存在資源搶占，在衡量資源的歸一化(如Rmax和Ravg)時采用公共資源的最大供應量比。功能集選擇的超啟發式最常用的六種功能運算符為“+”、“-”、“×”、“/”、“max”和“min”。

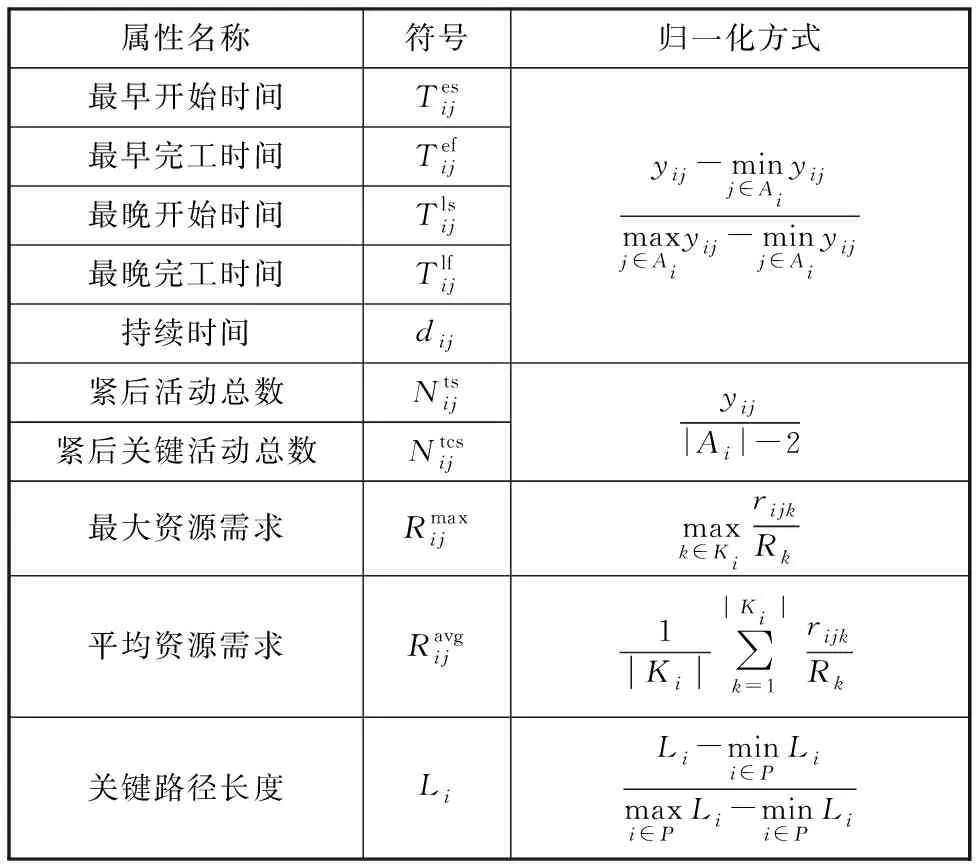
表1 優先級屬性

根據IGP流程，在第一個項目集下訓練時需要隨機初始化種群，隨機初始化種群中每個個體的頂層編碼以0.5的概率控制為Fall或Rise，下層結構樹則采用ramped half-and-half方法隨機生成，除頂層外，樹深度控制在2～6之間[29]，圖2所示的樹的深度為3。

(a)降序編碼結構

2.2 NSGA-Ⅱ評估和遺傳算子

IGP是應用于多目標RCMPSP下的求解PR訓練，因此需要建立相應PR的評估方式來實現進化過程中的基因取舍。多目標優化問題可以對每個目標賦予相應的權重轉化為單目標問題，但在大多數實際場景中，權重很難確定且可能變化，因此本文采用NSGA-Ⅱ[30]來分配虛擬適應度以實現PR個體評估，主要步驟如下。

(1)根據種群中個體計算的目標函數值，將整個種群進行分支配解分層，同層的解為非支配關系，上層個體支配下層個體，不同層級解的關系如下所示：

G1?G2?…?Gg?…?Gm

(8)

式中，m為當前種群分層后的最大層數；Gg為第g層個體。

(2)計算相同等級各個個體間的擁擠距離，由于不同目標同樣數量級不同，所以仍然需要歸一化，其計算公式如下：

(9)

式中，V為目標函數集合；ov,a為個體a在目標函數v下的值，下標a+1和a-1代表在目標函數值v下該非支配層中經排序后個體a的相鄰個體。

(3)根據支配等級和空間距離分配其虛擬適應度，即首先判斷個體所屬非支配層，層級越低越優，處于相同層級的個體擁擠距離越大越優。

除了PR個體的評估，在IGP的進化過程中需要用到傳統遺傳算子選擇、交叉和變異。其中選擇算子采用錦標賽選擇[31]；根據文獻[24]，交叉算子采用子樹交叉模式，即隨機數小于交叉率Pc時，兩父代個體交換部分子樹，而變異算子則是當隨機數小于變異率Pm時，用一個隨機生成的子樹替換父代個體某一節點下的子樹。此外，配合頂層判別編碼方式，在變異算子中增加判別變異方式，即當隨機數小于Pm時，父代個體的頂層編碼方式發生變化，如Fall編碼變化為Rise編碼，遺傳算子的執行順序如圖1所示。

2.3 多樣性種群更新

GP樹狀的編碼方式會使整個種群出現許多功能相似或相同但結構不同的編碼，如圖3所示。其中圖3a和圖3b雖然是兩種結構不同的編碼，但最終產生的優先級表達式是一致的；而圖3c和圖3d則是對同一個優先級表達值Tef進行平方和加倍處理，在調度過程中各個活動的Tef值相對大小是固定的，因此2Tef和(Tef)2的調度排序效果也是一致的。也正是因為上述兩種情況，傳統GP在進化搜索過程中因種群的多樣性降低而易陷入局部最優，導致訓練效果不佳。為此本文設計了一種種群更新方式，在更新過程中建立虛擬適應度FK存儲上一個工況的信息,作為更新是否舍棄當前個體的依據，以提升泛化性能。假設種群規模為Size,主要步驟如下：

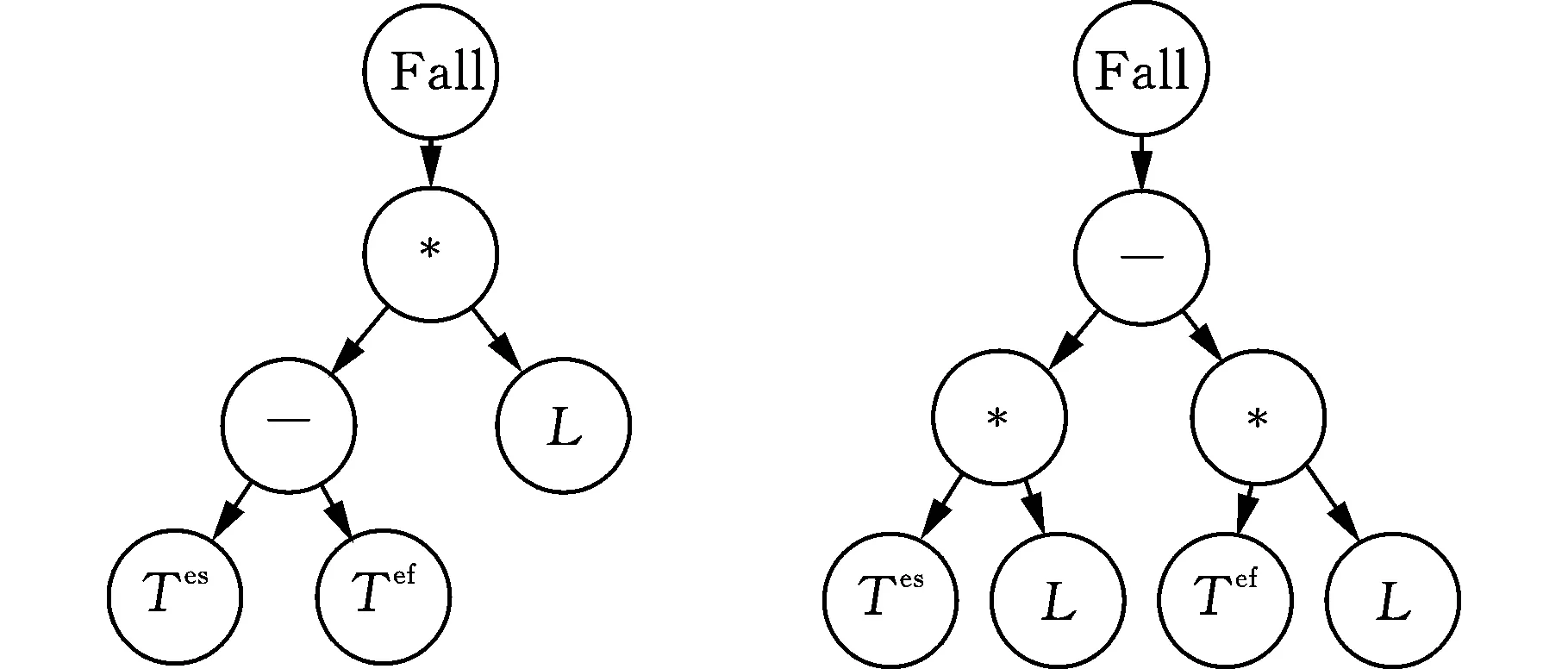
(a)相同功能結構PR1 (b)相同功能結構PR2

(1)建立相同個體臨時儲存集合Snew、Sold和不同個體臨時存儲集合D，計算遺傳算子更新后的新種群中每個子代個體的各個目標函數值，如果原種群中沒有目標函數值完全相同的父代個體，則該個體放入D，否則該子代個體的FK置為空(非支配層為0，擁擠距離為0)并放入Snew，對應的相同父代個體放入Sold。

(2)對于屬于Snew中的每個子代個體，解析其優先級表達式是否與對應的相同父代個體一致或相似，如果否那么將該子代個體移入集合D中。

(3)對于Snew中余下各個子代個體，判斷其對應父代個體FK是否為空，如果為空且隨機產生的判斷數小于0.5.則將該子代移入集合D中。

(4) 將D中的個體與原種群合并，選擇前Size個虛擬適應度最好的個體生成下一代種群并判斷是否為當前工況下的最大迭代次數，如果是，則將最終種群各個個體的虛擬適應度設置為該個體的FK值。

3 IGP性能驗證及比較

3.1 實驗環境和參數設置

IGP基于MyEclipse 2017開發，計算機配置為2.80 GHz雙核處理器，8 GB內存。根據文獻[16]，一個工況的項目集由4個活動數量不同的項目構成，分別來源于PSPLIB數據庫[32]中的J30、J60、J90和J120庫(每個項目包含30、60、90、120個非虛活動)，且項目集每種資源的最大單位供應Rk為20。選擇PSPLIB數據庫4個活動庫的前50組數據構成驗證數據集，其中前30組為訓練項目集，其余為測試集。IGP中所需參數根據經驗設定為：最大迭代次數Mgen=20，種群規模Size=200，交叉率Pc=0.9，變異率Pm=0.2。

3.2 評價方式

參考文獻[15]，采用性能排名對PR進行評價，即不同的PR調度同一個工況項目集時，根據目標函數的大小產生兩組排名(Q1和Q2)，用50組項目集下的平均排名W衡量PR調度性能的相對優劣，計算方式如下：

(10)

式中，M為項目集的總數量；wm,v,l為規則l在項目集m下調度目標v對應的排名值，其值為小于|Nrule|的正整數；Urule為參與排名的規則集合。

3.3 算例下IGP性能分析

IGP的訓練結果為一組HPR(Pareto解集)，采用IGP訓練10次，將第一次訓練產生的HPR與20種經典PR[15]的性能進行對比，如表2所示。表2中HPR1至HPR10為本次訓練得到的10種不同結構的HPR。10次訓練結果的統計表見表3。表3中，Npar為該次實驗得到的非支配HPR的數量，pdo為該次實驗訓練出的HPR的W值高于20種傳統PR的W值占所有非支配HPR的比例。

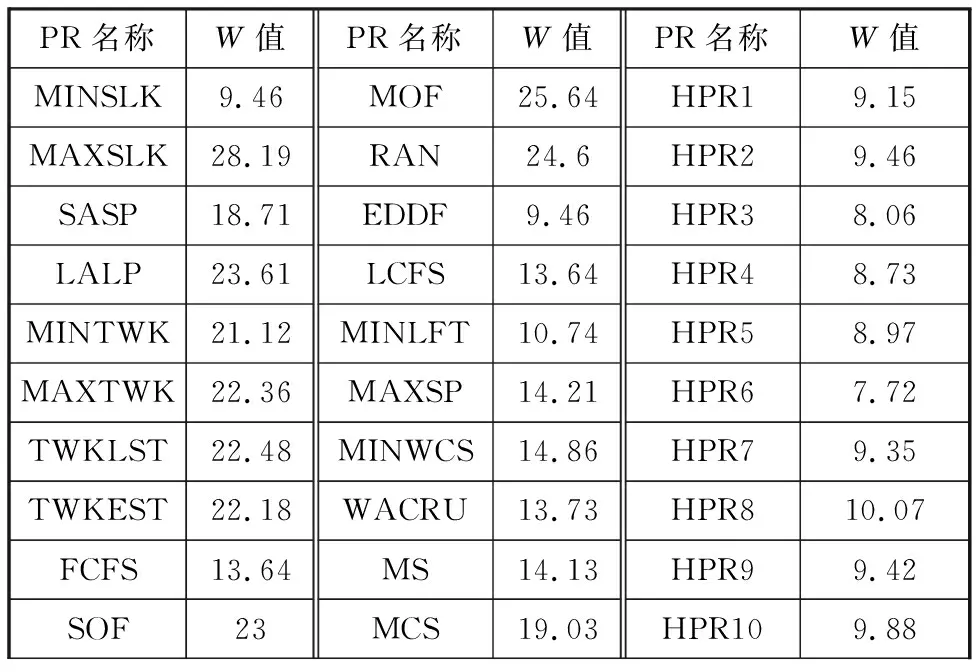
表2 傳統PR和HPR的W值

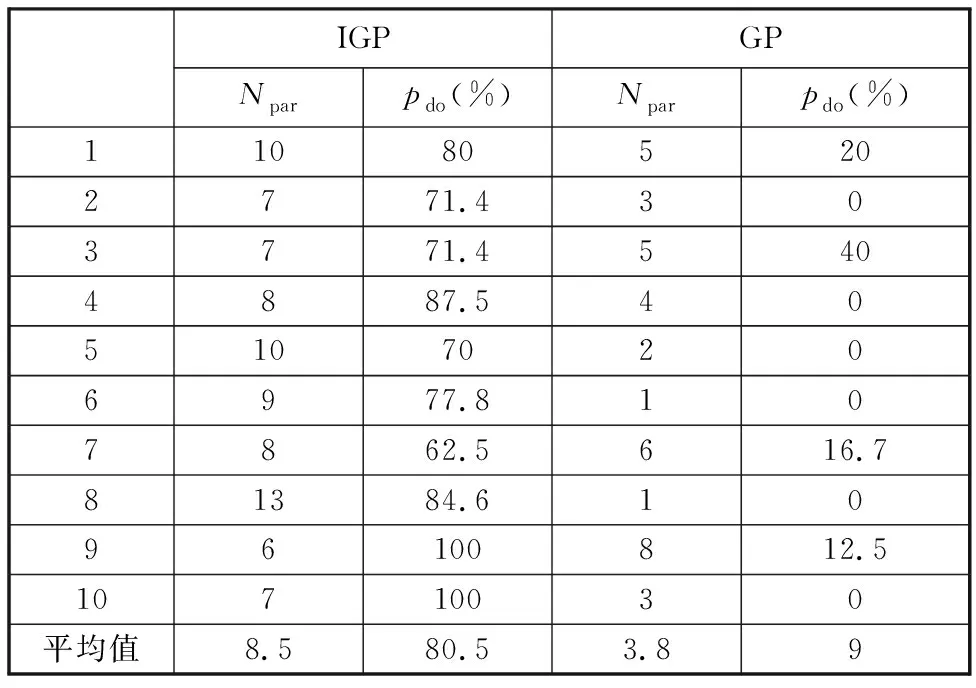
表3 HPR性能排名結果統計表

從表2中可以看出，IGP本次訓練得到的80% HPR(除HPR8和HPR10外)性能排名均高于20種傳統PR，而HPR8和HPR10性能排名僅次于EDDF和MINSLK兩種規則。從表3中可以看出，10次訓練產生的HPR優于20種傳統PR的占比平均值大于80%，而剩余20%規則也優于大部分傳統PR(表2)，由此可以得到IGP訓練的HPR調度能力比單一傳統PR更優秀，證明本文提出的IGP既保留了基于啟發式的PR的快速響應能力又解決了PR不具備優化能力的問題。

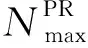
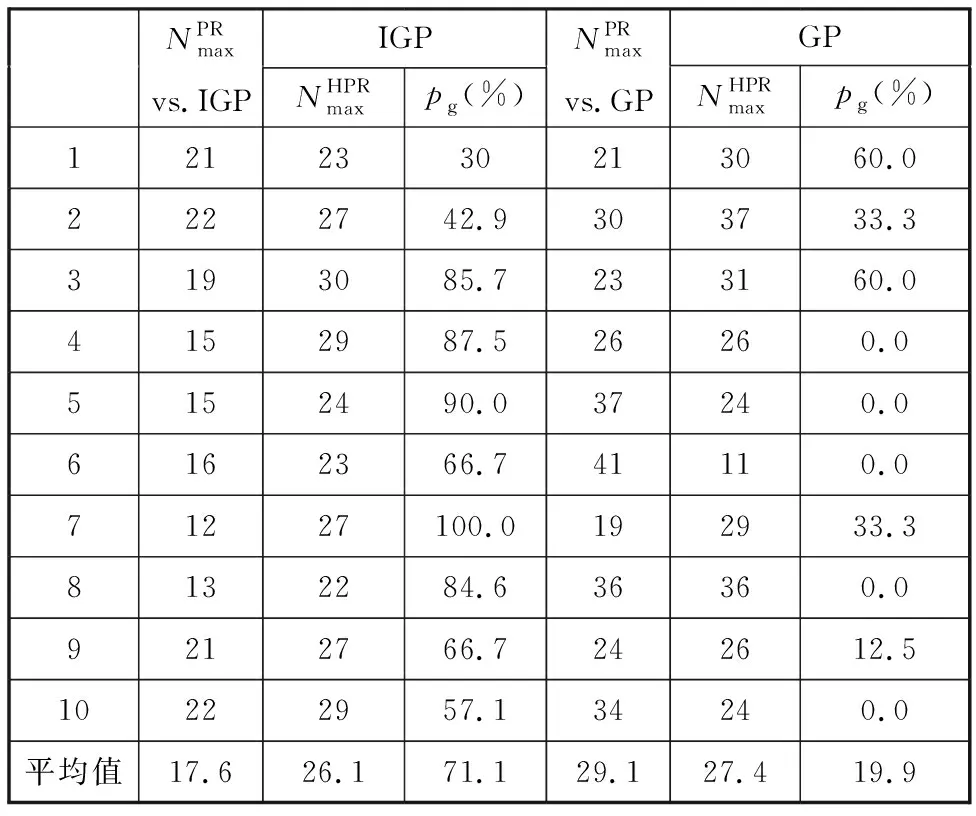
表4 HPR的Pareto前沿次數統計結果

從圖4中可以看出，相較于傳統PR，本文提出的IGP生成的HPR普遍目標函數值較小，處于支配地位。同時圖4中的Pareto前沿(Pareto前沿為HPR2、HPR5、HPR9、HPR4、WACRU和MS)大部分是IGP生成的HPR。從表4中可以看出，大多數訓練情況下，HPR的Pareto前沿次數最大值要遠高于傳統PR，同時平均有70%的HPR出現Pareto前沿的次數高于20種傳統PR，證明了IGP的有效性。

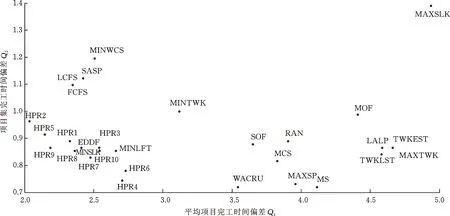
圖4 工況1下不同PR和HPR目標函數支配關系Fig.4 Objective function domination relationship of different PR and HPR under condition 1

現有GP超啟發式求解調度文獻較少，文獻[24-26]的重點在于GP在不同RCPSP問題上的實現，并非對GP的進化過程做出改進。為此，對比表3和表4可進一步證明本文提出的IGP訓練的有效性。從表3中可以看出，IGP訓練得到的Pareto解集中HPR的平均數量是8.5而GP為3.8，可以得出IGP能夠訓練出非支配解的范圍更廣，而GP由于相同/相似功能編碼的存在，非支配解的范圍大大降低。GP訓練的HPR支配20種傳統PR的占比平均值為9%，遠低于IGP，可以看出本文提出的IGP的訓練能力更強，更容易避免局部最優。從表4中可以看出，對于相同的傳統PR，GP生成的HPR的支配能力低于IGP，其Pareto前沿出現的次數較低甚至在某些訓練下要弱于傳統的PR。由此可以看出IGP訓練的HPR具備更強的通用性。

為進一步驗證IGP訓練出的HPR比現有啟發式算法具備更強的調度能力，選擇文獻[18]中的啟發式PSGS-SLK進行對比。第一次IGP訓練的HPR與PSGS-SLK調度50組算例的支配關系如表5所示，其中Nd為HPR支配PSGS-SLK的算例個數，Nnd為二者互為非支配關系的算例個數，Npd為PSGS-SLK支配HPR的算例個數。10次訓練后的結果統計表如表6所示，pd代表支配算例個體大于被支配算例個數的HPR(即Nd大于Npd)占該次訓練的所有HPR的比例。

通過表5和表6可以看出，大多數的HPR能夠實現大部分工況支配PSGS-SLK或與其成非支配關系，表明相較于現有的啟發式算法，IGP所訓練的HPR具備更好的調度能力。

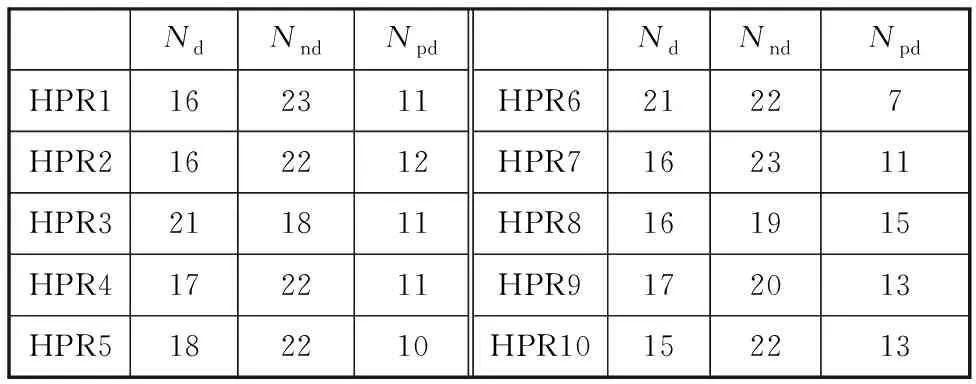
表5 HPR與PSGS-SLK支配關系表

表6 HPR與PSGS-SLK支配關系統計表

3.4 實例下IGP性能驗證

本文以某飛機總裝廠機電調試部分裝配作業為例對算法進行驗證。該廠采用兩條并行裝配線裝配兩種不同機型的飛機且均包括機電調試作業，對于同一架次飛機而言，該部分的調試工作會影響后續的裝配工作，因此既要考慮本架次飛機該工位的裝配時間最短又要考慮兩架飛機的總裝配時間最短。該部分裝配工作需要共用同一班組人員(總人數為18)和3種公用工裝(總數均為10)。兩種機型機電調試裝配作業的緊前緊后關系及所需資源通過掃描本文首頁OSID二維碼可見，該廠目前以最晚開工時間為優先級進行生成調度，即EDDF。通過關鍵路徑法可得項目1和項目2的關鍵路徑分別為50和55，而IGP第一次訓練后的HPR和EDDF的調度結果見表7，10次訓練結果見表8。表7中，C1和C2分別為項目1和項目2的完成時間，表8中Pd為支配EDDF的HPR占總的HPR的比例，Pnd為與EDDF互為非支配關系的HPR的比例。

從表7中可以看出，IGP生成的大多數HPR的調度性能要優于EDDF，且剩余HPR和EDDF相比各有優勢，在未分配權重時互為非支配關系，由此可以證明IGP能夠為RCMPSP調度帶來更多有效的HPR。在表8的統計結果中，除第7次訓練和第10次訓練IGP產生了EDDF支配的HPR(分別占比12.5%和28.6%)外，其余HPR均為支配EDDF或與EDDF互為非支配關系，且在大多數訓練情況下IGP生成的HPR支配EDDF的概率較大，驗證了本文提出的IGP在實例調度中的有效性。

表7 HPRs和EDDF的調度結果

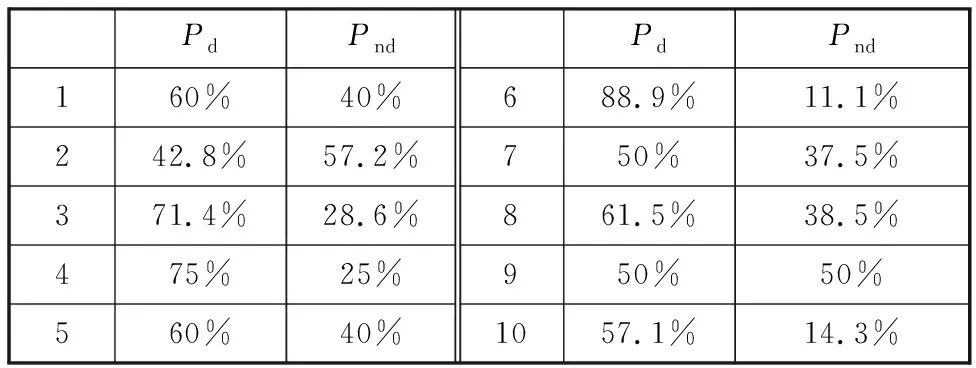
表8 HPR與EDDF的訓練結果

4 結論

為了實現多目標RCMPSP下的PR最優進化，本文對GP進行改進，提出一種IGP算法：

(1)通過現有的20種求解RCMPSP問題的PR，從資源、活動和項目的角度提取屬性，并根據屬性的類型設計了不同的歸一化方式，同時設計了判別編碼，確保最小化/最大化同一種優先級表達式均能迭代搜索，從而保證解空間的完整性。

(2)結合NSGA-Ⅱ的虛擬適應度分配的評估方法，不設置權重而是對種群中個體進行非支配分層并計算不同層個體的擁擠距離，從而評估個體的優劣。

(3)設計了一種多樣性種群進化更新方式以消除相同/相似功能編碼，避免傳統GP容易陷入局部最優的問題，提高了算法的搜索能力和泛化能力。

下一步研究可將該方法應用在動態RCPSP類問題下求解并結合魯棒性性能分析，使其獲得更廣泛的應用和達到更全面的快速求解。