滑模變結構控制中的機械臂運動軌跡仿真

張海濤

(合肥通用職業技術學院機械工程系 安徽合肥 230031)

在控制范疇中變結構自動控制系統屬邊緣學科，在當今己經發展成與其它系統可區分的控制學科，變結構控制體系不但在明確性與不明確性、線性和非線性系統中可以適用，而且還可以適用于集合控制和分散控制、持續和離散、集中參數與分散參數系統等系統。變結構控制實質是一類獨特的非線性控制系統，它的特點是控制系統機構的非靜態性，它能夠有方向變化，依據當前所處的狀態環境的改變，有目的的使系統按照預定“滑動模態”進行軌跡運動，這種基于“滑動模態”的軌跡控制過程，我們稱之為滑模控制。除此之外它還體現為控制的不連續性。非線性系統上的魯棒性和抗干擾性是滑模控制所表現的最大的優點，本文主要對六自由度機械臂在滑模變空結構中設計出一套通用的滑模控制器，以此優化機械臂在運動軌跡控制上的規劃問題。

一、機械臂位姿描述

如圖1所示為現代化生產線上經常使用到的PUMA560型機械臂。這種機械臂有6個可以自由運動的關節，分別是大臂、小臂、底座等組成。手臂的前端有3個自由度，分別是大軸底座的轉動為自由度1，肩部主軸的轉動為自由度2和肘部主軸的轉動為自由度3。通過安裝在底座軸中心的伺服電機來實現的機械臂機體繞主軸的回轉。機械臂是依靠安裝在內部的平衡裝置來控制大臂和小臂的平衡的。回轉平臺上安裝機械臂的大臂臺座。大臂上下擺動是通過安裝在內部的直流伺服電機實現的。大臂的臂體的前端關節處安裝了小臂,安裝在內部的伺服電機可帶動小臂的上下俯仰和小臂的回轉運動。手臂的后端有3個自由度，分別是手臂的轉動為自由度4，手腕軸的俯仰轉動為自由度5和機械臂的執行端的轉動為自由度6。通過伺服電機來控制機械臂的小臂前端的腕部的擺動和轉動。各個關節的協同合作，通過安裝在各個關節處的傳感器來收集信號并反饋給控制系統，最終完成事先編制好程序的各種指定工作[1]。

圖1 PUMA560機械臂連桿坐標系示意圖

機械臂PUMA560作為一個6自由度機械臂，它的結構是串聯開鏈結構，它的6個關節都是轉動關節，其中前3個關節用來確定機械臂末端的位置,后3個關節的軸線交于一點來確定機械臂末端執行器的位置。因此選取這個交點為機械臂末端執行器的參考點，機械臂桿件坐標參數如表1所示。

表1 PUMA560機械臂桿件坐標參數

二、滑動模態的控制

滑動模態變結構的控制過程主要是在切換面雙側，通過改變開關來實現系統結構發生改變，切換函數s(x)用表示，當s(x)=0時可以表示切換面。

通常的常非線性系統表達式如下：

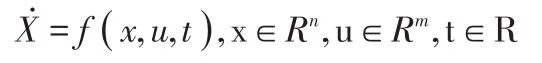
方程式中，x∈Rn記為體系的狀態向量，u∈Rm稱為控制向量。在式1的狀態環境中，當轉換成s(x,t)=s(x1,x2,...,xn)=0時兩個上下部分構成了狀態環境即，s〉0或s〈0。其中通常點、起始點和終止點是在s=0上點的三種情況，它們對應圖2中的A，B和C三類點。

圖2 切換面上三種點的特性

三種運動點可分為:

常點：當一點運動到s=0切換面周圍時保持其原有狀態，并且通過此點(對應圖中點A)。起點：當點運動到s=0周圍時，從轉換面的兩側遠離該點(對應圖中點B )。終點：當點運動到s=0周圍時，從轉換面兩邊接近這點(對應圖中點C)且停頓在上面[2]。

假如每個點全是終止點，在轉換面的某一區域內，只要接近該區域該點將會被“吸引”，那么將該周圍叫做“滑動模態”區。在滑動模態范圍內，若能夠滿足終止點的條件，在某一個運動點移動到轉換面s=0的周圍時則有：

其中u+(x) ≠u-(x)，滿足前面的條件使得：

(1)滑動模態是存在狀態；

(2)滑模面外的活動的點能夠在規定的時間內抵達滑模面，即符合以下公式：

(3)使其穩定性得到保證；

(4)符合動態品質的基本要求。

符合這四個條件時就稱之為滑模變結構控制。這四個條件也是滑模控制的四個基本條件。

三、基于RBF滑模變結構的控制算法

RBF具有很強的逼近能力，在前饋神經它具有訓練速度快，方法簡單，不會產生極小值，它的輸出值和權值都成線性關系等特點，因此用RBF進行滑模控制結構。

RBF滑模變控結構設計是將切換函數連接到神經網絡RBF輸入端中，將滑模控制器的輸入端與神經網絡RBF的輸出端連接[3]。RBF滑模變結構控制器結構圖如下圖3所示。

圖3 RBF滑模變結構控制器結構圖

將一個被控對象為

的系統，設r(t)為它的位置指令，設為它的切換函數。

基于RBF滑模控制器設計在滑模控制器的前端，RBF網絡的輸出端用字母u 表示輸出，輸出結果作為滑模變結構控制器的輸入值。即m作為隱含層神經元的個數。RBF網絡通過不斷調整權值E，使得的值趨向于0，實現滑模變結構控制的目的。

四、笛卡爾坐標系下的機械臂

把機械臂放置笛卡爾坐標系中，對其中的各個關節進行軌跡參數的設定，在t為0時設置初始參數，根據機械臂的軌跡進行運算，每個時間加量△t產生一個數值，對應于機械臂關節所處的位置。通過笛卡爾坐標系的變換，產生相對應的關節變量值，對這兩個過程中所產生的位置信息進行比較，如果不同，則重新返回計算，如果相同，則可以退出循環，算法計算結束。由于在位置求解過程中，關節的數量較多，必須引入矩陣計算，在得知位置結果的情況下求解過程信息對矩陣的逆計算，如圖4所示。

圖4 笛卡爾坐標系下的關節算法

在笛卡爾坐標系中進行機械臂的軌跡規劃，需要對機械臂關節位置的逆運動學求解，其中最主要的問題是，在通過笛卡爾坐標系變換的情況下，已知機械臂末端位置來求解機械臂各關節在運動過程中的空間坐標，這是相當困難的。但是通過上述算法過程，我們可以按照如下步驟完成對機械臂關節的逆運動學求解：

（1）笛卡爾坐標系內機械臂末端空間點的選擇可以是任意的，也可以是按照規律最初設定好的，但是空間點的坐標必須是連續變化的。

（2）跳躍空間節點的選取必須通過擬合曲線來求解，在位置空間位置的情況下，通過插值函數，求解中間數值，在插值節點數足夠多的情況下，擬合曲線是光滑的。對于笛卡爾坐標系內擬合曲線的求解，與機械臂本身的結構特性有關。相對于本文中所示的六自由度機械臂，可以通過增加插值函數內的點來進行快速求解[4]。

五、六自由度機械臂滑模變結構控制的設計

滑動模態是指滑動模態運動軌跡限制在某個理想的區域，它可以解決當使用切換函數而引起的抖振問題時，可以通過準滑動模態控制器的方法來解決滑模控制的抖振問題。當準滑動模態滿足＜0條件時，它就要求在滑動模態的切面區域上進行變結構切換。在現實生活中許多的系統應用中都應用到了滑動模態能夠減弱抖振問題。本節中準滑動模態控制器將原來的控制器函數符號sgn(s)使用飽和函數符號sat(s)，來進行替換。

圖5 飽和函數

s的線性函數使用sat(s)符號表示，所以根據線性函數的特點，可知它的反饋控制也是連續性的,另外切換控制方法也可以使用在邊界層外[5]。通過對滑模控制進行各個自由度的解耦，可以把系統模型劃分成六塊小的子系統，然后在進行對各個子系統進行劃面切換設計，這樣能夠快速的確定趨向原點的各個滑動模塊。

六、基于滑模變結構控制的機械臂運動軌跡仿真

根據表1中關于PUMA560機械臂桿件坐標參數，在MATLAB軟件中，可以使用相應的功能插件，功能插件對應的工具條可以對機械臂的相應參數進行設定，為了實現對機械臂軌跡的仿真，根據前述表格的機械臂各關節節點在笛卡爾坐標系下的初始位置，需要對軟件參數進行相應的設定，以方便后續運算的系統調用。

動態環境下遇到障礙的機械臂軌跡路徑規劃，“動態環境”的界定主要是指在機械臂的軌跡規劃過程中，可能在任意位置出現障礙，這種出現是隨機的，不是設定好的，而系統可以根據這種隨機出現的障礙進行軌跡規劃的調整，并規劃出合理的滿足要求的運行軌跡。

依據功能插件對機械臂初始參數進行輸入，在輸入的過程中要注意輸入的順序，以防止由于參數順序錯誤導致軌跡運動無法正常進行，相關空間曲線坐標點如表2所示。

表2 空間曲線坐標點

運行MATLAB軟件，在 Robotics Toolbox 工具欄，使用link 函數用來創建一個桿件，它有兩種創建方法，文中使用了改進的D-H（modified）參數，分別對應于兩種坐標系的進行參數設置。還有一種是采用標準的D-H參數（standard），本文并未使用。

在對系統參數進行設定的過程中，元素0代表轉動關節，元素1代表移動關節。Link的另外四個參數α,a,d,θ，分別表示如下：連桿兩端軸線之間的公垂線的長度定義成連桿的長度α，連桿的扭角a定義成連桿兩端軸線在公垂線方向的夾角。相鄰連桿的長度在關節軸線上的距離定義成關節的平移量d，相鄰連桿的長度在關節軸線上的夾角定義成關節的轉量θ。

在MATLAB環境下，創建機械臂，根據表2的參數和數據，構建機械臂的仿真程序如圖6所示。顯示的是機械臂在MATLAB繪圖空間的三維圖，表示機械臂處在初始位置θ為0，可以通過調節控制面板中相應按鈕來使機械臂的末端節點發生變化。

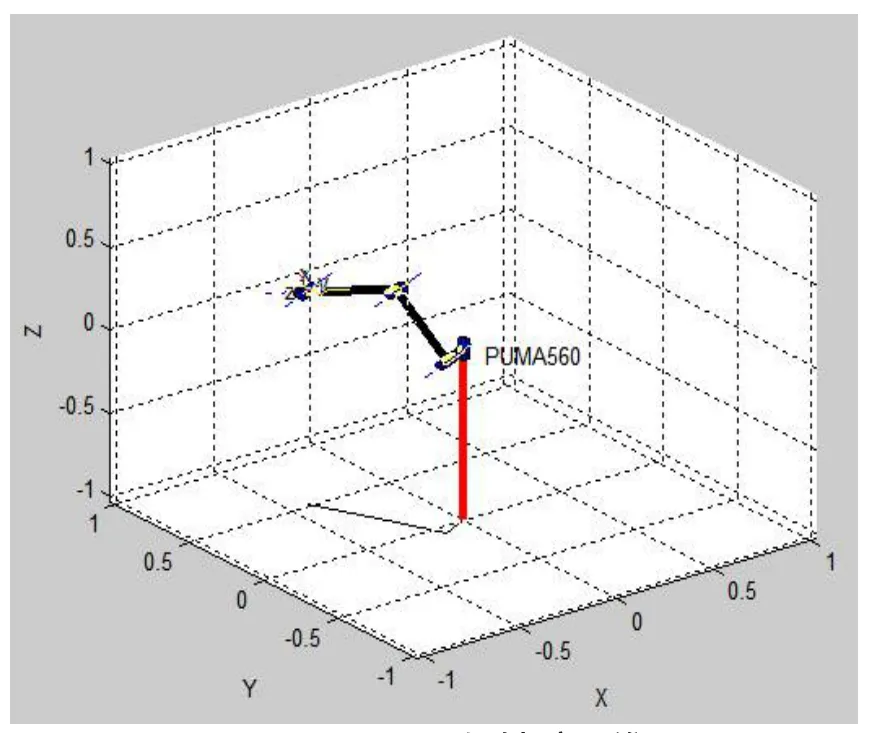
圖6 PUMA560機械臂三維圖

在機械臂的笛卡爾空間中，機械臂的末端節點依據函數設置運動軌跡，并設置機械臂末端節點的初始點坐標和終點坐標，為了實現了機械臂末端節點正運動學的求解，先求得機械臂末端相對于基坐標系的位置坐標為(0.372，0.259，-0.531)，機械臂在起點和終點的位置如圖6所示。

根據齊次變換矩陣求得到機械臂由初始位姿到末端位姿時的各關節變量。

對機械臂由R點到Z點的運動軌跡進行仿真，選擇六關節機械臂末端的2個關節，假設它們的期望軌跡為

通過MATLAB的相關函數可以繪出機械臂由R點運動到Z點，各關節隨時間變換的位置、速度和加速度圖像。

機械臂在笛卡爾空間軌跡規劃運動過程中，可能遇到未知狀態下的障礙物，這個需要在軟件仿真情況下加以設定，障礙物的設定是隨機的，可以出現在笛卡爾空間的任何位置，也可以以任何狀態出現，可以是圓形的物體或矩形的物體或其他空間物體得到形狀。機械臂的各關節在滑動模態控制下，應該能夠自主進行避障，并且在運行的過程中保持機械臂關節的速度和加速度平滑的過度，沒有劇烈的振動。這是對機械臂仿真軌跡控制的一般要求，通過笛卡爾空間坐標系的有效驅動函數得以實現。以下為機械臂PUMA560各個關節添加的關節函數如下表3所示：

表3 機械臂的關節函數

根據以上分析可以知道機械臂的各關節的角速度曲線比較平滑，機械臂的末端節點在運動的過程中能夠有效避開不規則形狀的空間物體，并且機械臂的其它節點的速度和加速度能夠在穩定狀態下運動，沒有出現明顯的振動現象。

如圖7和8所示為機械臂各關節的角速度和角加速度的曲線，從這兩個曲線圖可以看出，機械臂的關節在運動過程中的角速度和角加速度均能夠光滑平穩過度。

圖7 機械臂各關節的角速度

圖8 機械臂各關節的角加速度

在機械臂軌跡規劃過程中，末端節點的位置、速度、加速度曲線如圖9所示。由機械臂關節軌跡仿真圖可得，軌跡之間的差異很小，并且能和期望的軌跡線幾乎重合，機械臂關節運動軌跡的精確度較高，在很短的時間內機械臂的振動得到了收斂，在規避障礙物過程中能夠有效規避障礙物，并且整個運動軌跡的運行所使用的時間較短，精確性能良好不受外界環境變化的干擾。

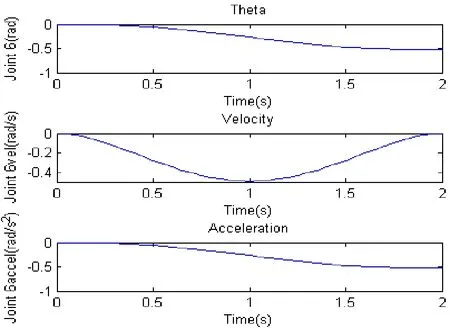
圖9 末端節點的位置、速度及加速度曲線圖

由圖10機械臂仿真結果可得出，第一個機械臂始終與障礙物保持著0.2rad的距離繞開障礙物。分別在運動到第25s和40s時候，以平滑的曲線軌跡繞開了前方的障礙。同樣也可以得出第二個機械臂關節，與障礙物保持著0.2rad的距離繞開障礙物。分別在運動到第32s和42s時候，以平滑的曲線軌跡繞開了前方的障礙。最終使得機械臂能夠安全的到達目標位置。雖然在移動的軌跡過程中兩個關節之間存在微小的波動，但是期望的路線都能夠在較短的周期內并且精確度較高的實現，性能良好，不受外界的干擾，并且魯棒性很強。

圖10 機械臂末端節點的運動軌跡

七、結論

本文以六自由度機械臂為例，研究機械臂在運動過程中的仿真軌跡，在笛卡爾坐標下建立機械臂的位姿描述，然后建立基于RBF滑動模塊變結構的控制算法，通過滑動模塊控制的引入，在MATLAB軟件環境中建立笛卡爾坐標系下數學模型，設置軌跡參數的初狀態和終狀態，最后生成機械臂末端節點在規避障礙物過程中的運動軌跡，通過運動仿真的輸出參數可以看出，在運動過程中的速度、加速度等參數光滑過度，能有效避開在機械臂運動過程中出現的障礙物，解決了機械臂在運動過程中的振動問題和規避障礙物的問題，在工業自動化應用中居有一定的現實指導意義。