基于靈敏度的六自由度并聯(lián)機(jī)構(gòu)誤差分配方法

譚 爽，梁鳳超，陳 龍，林 喆，康建兵

（北京空間機(jī)電研究所，北京 100090）

0 引言

由于受到發(fā)射力學(xué)環(huán)境、在軌重力場(chǎng)和溫度場(chǎng)等因素的影響，空間光學(xué)載荷系統(tǒng)入軌后部組件易產(chǎn)生相對(duì)位姿失配和面形誤差，導(dǎo)致光學(xué)載荷的探測(cè)性能偏離原有設(shè)計(jì)、系統(tǒng)探測(cè)性能和成像質(zhì)量嚴(yán)重衰減［1-2］。對(duì)于傳統(tǒng)中小口徑光學(xué)載荷系統(tǒng)，通常采用先進(jìn)的熱控、輕量化、桁架、重力卸載等技術(shù)手段，弱化入軌后重力場(chǎng)和溫度場(chǎng)變化所造成的影響，從而保證光學(xué)系統(tǒng)的探測(cè)性能和成像質(zhì)量［3-5］。而對(duì)于大口徑高性能光學(xué)載荷系統(tǒng)，其部組件尺寸更大，受熱力場(chǎng)與重力場(chǎng)變化的影響更敏感，探測(cè)性能和成像質(zhì)量對(duì)部組件位姿及面形精度的要求更加精確，傳統(tǒng)的輕量化、無(wú)熱化等被動(dòng)技術(shù)手段已無(wú)法滿(mǎn)足大口徑高性能光學(xué)載荷的宇航工程需求。針對(duì)這一工程難點(diǎn)，國(guó)外已采用主動(dòng)光學(xué)與自適應(yīng)光學(xué)的方法，在光學(xué)載荷系統(tǒng)中增加精密主動(dòng)調(diào)整控制裝置，在軌矯正部組件的相對(duì)位姿失配與面形誤差，確保大口徑高性能光學(xué)載荷在軌運(yùn)行時(shí)的探測(cè)性能和成像質(zhì)量［6-8］。在工程實(shí)現(xiàn)方面，國(guó)外主要采用六自由度并聯(lián)機(jī)構(gòu)作為次鏡或拼接主鏡的位姿調(diào)整機(jī)構(gòu)［9-11］。六自由度并聯(lián)機(jī)構(gòu)有精度高，剛度大，動(dòng)態(tài)性能好和摩擦小等優(yōu)點(diǎn)［12-14］。

大口徑光學(xué)載荷系統(tǒng)對(duì)六自由度并聯(lián)機(jī)構(gòu)的精度要求可達(dá)到亞微米級(jí)與角秒級(jí)，對(duì)六自由度并聯(lián)機(jī)構(gòu)精度指標(biāo)較為嚴(yán)格，因此在設(shè)計(jì)時(shí)必須進(jìn)行精度分析與誤差分配［15-16］。精度分析是根據(jù)六自由度并聯(lián)機(jī)構(gòu)各組成部件的加工誤差和安裝誤差，分析它們對(duì)六自由度并聯(lián)機(jī)構(gòu)位姿誤差的影響，修改相關(guān)誤差參數(shù)，以達(dá)到期望的精度指標(biāo)。誤差分配是根據(jù)并聯(lián)機(jī)構(gòu)位姿精度指標(biāo)的要求，反求應(yīng)分配給各組成部件的制造誤差和安裝誤差，并使其達(dá)到一定的均衡。

在并聯(lián)機(jī)床的精度分析領(lǐng)域，已經(jīng)有一些學(xué)者進(jìn)行了探討，但在精度綜合領(lǐng)域，目前研究還較少。在誤差綜合中，由于位姿誤差與鉸點(diǎn)誤差關(guān)系高度非線性與強(qiáng)耦合，在給出精度指標(biāo)要求時(shí)，無(wú)法利用誤差模型直接求出鉸點(diǎn)誤差。盧強(qiáng)等［17］利用蒙特卡洛法，綜合考慮零部件制造公差和運(yùn)動(dòng)副配合間隙誤差，對(duì)六腿并聯(lián)機(jī)床進(jìn)行了精度綜合。該方法具有過(guò)程清晰、編程簡(jiǎn)單的優(yōu)點(diǎn)，但Monte Carlo方法計(jì)算精度的可靠性體現(xiàn)在樣本點(diǎn)的容量，對(duì)一個(gè)位姿，樣本容量為（10～100）×104，如果在全工作空間內(nèi)進(jìn)行位姿精度分析，其計(jì)算量巨大，難以實(shí)現(xiàn)。趙永杰等［18］運(yùn)用誤差獨(dú)力作用原理和原始誤差等效原則，將誤差模型線性化，進(jìn)行誤差綜合，使并聯(lián)機(jī)器人精度綜合變得簡(jiǎn)單可行，但是忽略了模型的耦合性。趙新華等［19］以6-SPS并聯(lián)機(jī)器人機(jī)構(gòu)為例，在結(jié)構(gòu)誤差敏感方向建立了桿長(zhǎng)誤差與位姿誤差之間的解析關(guān)系，得出誤差影響系數(shù)，該方法在某一位姿時(shí)只需要計(jì)算一個(gè)方程組，就能夠?qū)崿F(xiàn)精確、定量的誤差分析，但沒(méi)有考慮鉸點(diǎn)位置誤差關(guān)系，無(wú)法為鉸點(diǎn)安裝與制作提供指導(dǎo)依據(jù)。

本文建立六自由度并聯(lián)機(jī)構(gòu)誤差模型，并利用誤差模型定義鉸點(diǎn)誤差的靈敏度，給出位姿誤差一定時(shí)鉸鏈鉸點(diǎn)位置誤差分配方法，避免了大量運(yùn)算。該方法簡(jiǎn)單高效，適用于六自由度并聯(lián)機(jī)構(gòu)鉸點(diǎn)誤差分析。

1 理論基礎(chǔ)

Stewart平臺(tái)是典型的六自由度并聯(lián)機(jī)構(gòu)，本文研究的是如圖1 所示的6-UCU并聯(lián)機(jī)構(gòu)：該機(jī)構(gòu)上下平臺(tái)以6 個(gè)分支相連，每個(gè)分支兩端是兩個(gè)胡克鉸，中間是一圓柱副。驅(qū)動(dòng)器推動(dòng)圓柱副作相對(duì)移動(dòng)，改變各桿的長(zhǎng)度，使上平臺(tái)變化在空間的位置和姿態(tài)。

圖1 6-UCU型Stewart并聯(lián)機(jī)構(gòu)

上下平臺(tái)各個(gè)鉸鏈點(diǎn)分別記作bi和Bi（i=1，2，…，6），分布為：bi分布在半徑為r的圓上，且b1、b3、b5和b2、b4、b6分別構(gòu)成2 個(gè)正三角形，其相對(duì)夾角為α，如圖2（a）所示；Bi分布在半徑為R的圓上，且B1、B3、B5和B2、B4、B6分別構(gòu)成2 個(gè)正三角形，其相對(duì)夾角為β，如圖2（b）所示。零位姿時(shí)上下鉸點(diǎn)所在平面之間的距離為六自由度并聯(lián)機(jī)構(gòu)的高度H，桿長(zhǎng)記為L(zhǎng)0。r、α、R、β和H決定了六自由度并聯(lián)機(jī)構(gòu)的構(gòu)型，為結(jié)構(gòu)參數(shù)。

圖2 Stewart平臺(tái)鉸點(diǎn)分布

并聯(lián)機(jī)構(gòu)常用的誤差模型在只考慮幾何誤差的情況下，非幾何誤差因素對(duì)并聯(lián)機(jī)構(gòu)運(yùn)動(dòng)精度的影響較小，于是在建立Stewart六自由度并聯(lián)機(jī)構(gòu)的誤差模型時(shí)可忽略非幾何誤差因素，只考慮安裝誤差、制造誤差和桿長(zhǎng)誤差等系統(tǒng)誤差。系統(tǒng)誤差考慮以下幾點(diǎn)：

（1）安裝誤差。對(duì)Stewart并聯(lián)機(jī)構(gòu)而言，固定在動(dòng)平臺(tái)與靜平臺(tái)上的鉸鏈安裝誤差參數(shù)共有36 個(gè)獨(dú)立參數(shù)。

（2）制造誤差。鉸鏈本身受加工精度和安裝精度的限制，其回轉(zhuǎn)軸線間并不可能理想的垂直，運(yùn)動(dòng)中心不可能重合于一點(diǎn)，這些都影響著鉸鏈的運(yùn)動(dòng)精度。

（3）桿長(zhǎng)誤差。驅(qū)動(dòng)支鏈桿在加工過(guò)程中受到加工精度的影響，其初始長(zhǎng)度也會(huì)存在誤差，一共6 個(gè)獨(dú)立的長(zhǎng)度誤差參數(shù)dli（i=1，2，…，6）。

鉸鏈的安裝誤差和制造誤差最終造成鉸鏈旋轉(zhuǎn)鉸點(diǎn)有位置偏差，即鉸點(diǎn)位置誤差，一共有36 個(gè)：dcj（Δxbi，Δybi，Δzbi和ΔxBi，ΔyBi，ΔzBi）（i=1，2，…，6，j=1，2，…，12）。因此，對(duì)于一般的Stewart 平臺(tái)，為了減小標(biāo)定模型的復(fù)雜性，在進(jìn)行誤差建模的過(guò)程中只考慮鉸點(diǎn)誤差和桿長(zhǎng)誤差共計(jì)42 項(xiàng)獨(dú)立的機(jī)構(gòu)參數(shù)誤差，并進(jìn)行誤差數(shù)學(xué)建模。

對(duì)上平臺(tái)進(jìn)行歐拉旋轉(zhuǎn)：①首先繞動(dòng)坐標(biāo)系z(mì) 軸轉(zhuǎn)動(dòng)Ψ；②然后繞動(dòng)坐標(biāo)系y 軸轉(zhuǎn)動(dòng)φ；③最后繞動(dòng)坐標(biāo)系x軸轉(zhuǎn)動(dòng)θ。

由上平臺(tái)向慣性參考坐標(biāo)系投影，可得表示上平臺(tái)姿態(tài)的方向余弦陣為

式中：

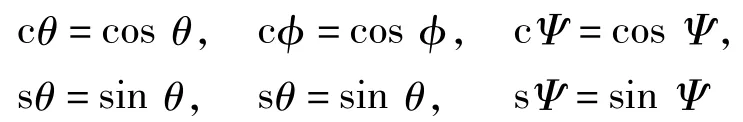
當(dāng)給定機(jī)構(gòu)的各個(gè)結(jié)構(gòu)尺寸和動(dòng)平臺(tái)的位姿后，可確定動(dòng)平臺(tái)鉸鏈點(diǎn)在動(dòng)坐標(biāo)系中的坐標(biāo)Pbi，再通過(guò)旋轉(zhuǎn)矩陣的變換可求出動(dòng)平臺(tái)鉸鏈點(diǎn)在靜坐標(biāo)系中的位置qbi，即

這時(shí)，支桿桿長(zhǎng)矢量li可在固定坐標(biāo)系中表示為

式中：li為第i個(gè)支桿的桿長(zhǎng)；ni為第i 個(gè)支桿的單位向量；Bi為靜平臺(tái)鉸第i個(gè)鉸點(diǎn)在靜坐標(biāo)系中的坐標(biāo)。

對(duì)式（3）進(jìn)行全微分，得：

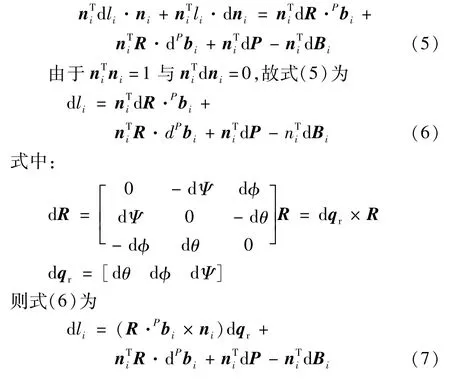
綜合6 個(gè)驅(qū)動(dòng)支桿，式（7）整理成矩陣形式，可得：

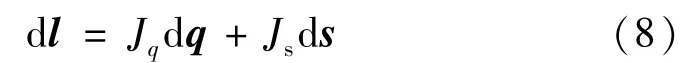
式中：

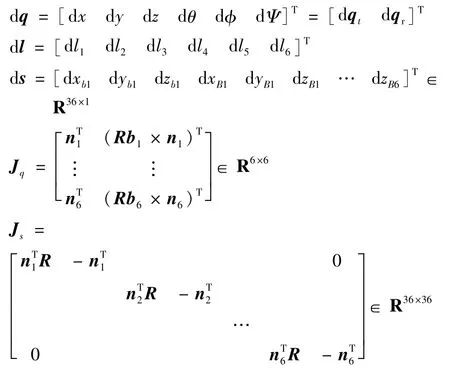
將式（8）整理成六自由度并聯(lián)機(jī)構(gòu)的誤差模型：

式中，

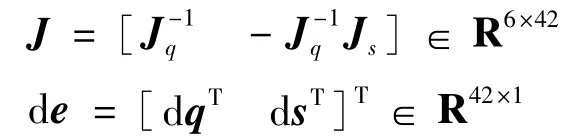
dq為動(dòng)平臺(tái)位姿誤差矢量；dl 為6 個(gè)支桿的桿長(zhǎng)誤差；ds為動(dòng)、靜平臺(tái)鉸鏈的鉸點(diǎn)位置誤差；de是包含dl與ds 42 項(xiàng)獨(dú)立的機(jī)構(gòu)參數(shù)誤差；J是六自由度并聯(lián)機(jī)構(gòu)結(jié)構(gòu)參數(shù)存在誤差情況下的誤差傳遞矩陣，即誤差傳遞雅克比矩陣。

2 鉸點(diǎn)誤差分配方法

考慮到桿長(zhǎng)誤差可以在控制算法中補(bǔ)償，因此為了簡(jiǎn)化誤差分配的難度，在誤差分配時(shí)只考慮鉸點(diǎn)誤差，即dl=［0 0 0 0 0 0］，代入式（9）可得：

因?yàn)镴s不是方形矩陣，無(wú)法求逆，因此當(dāng)已知六自由度并聯(lián)機(jī)構(gòu)位置與姿態(tài)誤差時(shí)，無(wú)法根據(jù)式（10）的逆向運(yùn)算求得鉸點(diǎn)誤差。為解決該問(wèn)題，引入矩陣奇異值進(jìn)行精度誤差分析。

為了將六自由度并聯(lián)機(jī)構(gòu)每個(gè)鉸點(diǎn)誤差與機(jī)構(gòu)的位置誤差與姿態(tài)誤差分別對(duì)應(yīng)，令：

從式（11）可知，J1j與J2j分別為六自由度并聯(lián)機(jī)構(gòu)的第j個(gè)鉸點(diǎn)對(duì)位置和姿態(tài)的誤差傳遞矩陣，對(duì)J1j與J2j進(jìn)行奇異值分解，分析誤差傳遞特性，可以得到機(jī)構(gòu)鉸點(diǎn)誤差和位姿誤差的傳遞特性，即機(jī)構(gòu)誤差傳遞靈敏度評(píng)價(jià)指標(biāo)。

以J1j為例，設(shè)鉸點(diǎn)誤差向量滿(mǎn)足≤ρ，根據(jù)式（11）有

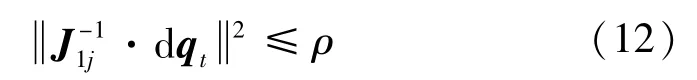
對(duì)誤差傳遞矩陣F進(jìn)行奇異值分解，得

式中：U=［u1，u2，…，um］和V=［v1，v2，…，vm］分別是和的特征向量矩陣，且Σ=［diag（σ1，σ2，…，σm）0］，σi是J1j的奇異值項(xiàng)（σ1≥σ2≥…≥σm≥0）。則J1j的逆矩陣為

式中

將式（14）代入式（12）有：

定義J1j和J2j矩陣的奇異值最大值為并聯(lián)機(jī)構(gòu)鉸鏈鉸點(diǎn)靈敏度（EAF），

當(dāng)鉸點(diǎn)位置誤差一定時(shí)，靈敏度值越大，對(duì)應(yīng)的機(jī)構(gòu)位姿誤差也就越大，機(jī)構(gòu)位姿精度就越低；反之，當(dāng)位姿誤差一定時(shí)，靈敏度值越大，鉸點(diǎn)位置誤差值也就越小，即鉸點(diǎn)精度就越高。

對(duì)于六自由度并聯(lián)機(jī)構(gòu)，當(dāng)位姿誤差為dq 時(shí)，可得鉸點(diǎn)位置誤差dcj應(yīng)滿(mǎn)足：

式中

在復(fù)合運(yùn)動(dòng)不同位姿中，對(duì)每一個(gè)誤差傳遞矩陣，先根據(jù)式（16）計(jì)算每個(gè)鉸點(diǎn)在相應(yīng)位姿時(shí)的EAF，再取整個(gè)過(guò)程中每個(gè)鉸點(diǎn)對(duì)應(yīng)的EFA最大值，為整個(gè)運(yùn)動(dòng)過(guò)程中該鉸點(diǎn)的EAF。最后根據(jù)式（17）可求出每個(gè)鉸點(diǎn)的位置誤差，用來(lái)指導(dǎo)鉸鏈的加工與安裝。

3 某型號(hào)六自由度并聯(lián)機(jī)構(gòu)的鉸鏈鉸點(diǎn)誤差分析

對(duì)于某空間光學(xué)遙感系統(tǒng)中六自由度并聯(lián)機(jī)構(gòu)精度要求為平移精度2 μm，旋轉(zhuǎn)精度2″，即19.39 μrad，結(jié)構(gòu)參數(shù)如下：r=239.51 mm，R=249 mm，H=195.03 mm，α=0.23 rad，β=0.268 rad。

為能夠計(jì)算出各個(gè)鉸點(diǎn)的EFA，需要讓上平臺(tái)運(yùn)動(dòng)到所有要求的六維工作空間。為簡(jiǎn)化計(jì)算量，給定上平臺(tái)低頻平移自由度運(yùn)動(dòng)規(guī)律與高頻轉(zhuǎn)角自由度運(yùn)動(dòng)規(guī)律的復(fù)合運(yùn)動(dòng)，如表1 所示。以此為仿真規(guī)律，仿真總時(shí)間為60 s。

表1 復(fù)合運(yùn)動(dòng)仿真規(guī)律

在復(fù)合運(yùn)動(dòng)中，以時(shí)間0.1 s為步距，在MATLAB中編程，計(jì)算每個(gè)鉸點(diǎn)在所有位姿下的靈敏度EAF值，如圖3 所示。由圖可以看出，不同位姿對(duì)應(yīng)的靈敏度是不一樣的。但靈敏度數(shù)值不會(huì)相差過(guò)大，始終在一個(gè)數(shù)量級(jí)上。取最大值為在該復(fù)合運(yùn)動(dòng)中鉸點(diǎn)的EAF，如表2 所示。

圖3 位姿位差對(duì)鉸鏈鉸點(diǎn)誤差的靈敏度

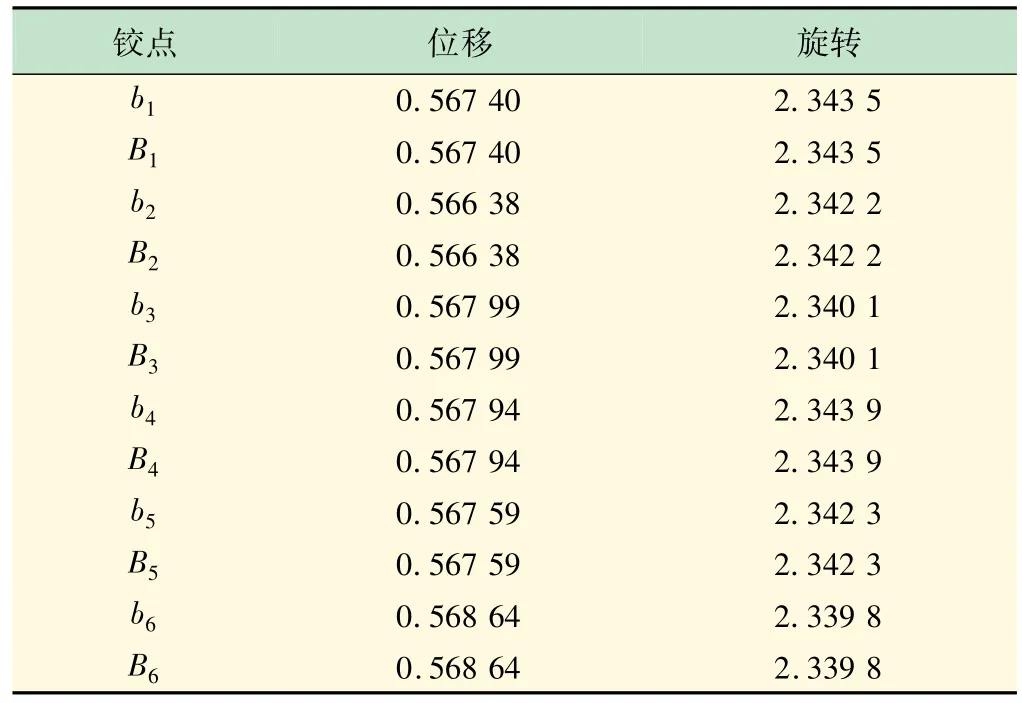
表2 運(yùn)動(dòng)范圍內(nèi)不同鉸點(diǎn)對(duì)應(yīng)的EAF

當(dāng)給出位姿誤差（即動(dòng)平臺(tái)運(yùn)動(dòng)精度）時(shí)，先合理分配位姿誤差，這里考慮工作范圍內(nèi)，鉸點(diǎn)誤差的占比是一樣的，均勻分配給每個(gè)鉸點(diǎn)，則對(duì)于鉸點(diǎn)b1，有dqt_b1=dqt/12dqr_b1=dqr/12，其位置誤差在半徑為dqt_b1的包絡(luò)球內(nèi)，姿態(tài)誤差在半徑為dqr_b1的包絡(luò)球內(nèi)。根據(jù)式（16）可以求出鉸點(diǎn)b1位置誤差：

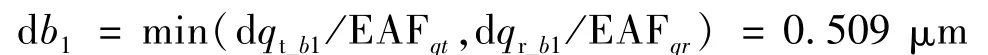
對(duì)鉸點(diǎn)b1，其位置誤差應(yīng)該在半徑為0.508 μm 的包絡(luò)球內(nèi)。

同理可求出每個(gè)鉸點(diǎn)的位置誤差，如表3 所示，可以知道每個(gè)鉸鏈在加工與安裝過(guò)程中造成的鉸點(diǎn)位置誤差應(yīng)該在某個(gè)包絡(luò)尺寸內(nèi)。

表3 鉸鏈鉸點(diǎn)位置誤差

可以得到，每個(gè)鉸點(diǎn)的位置誤差在同個(gè)數(shù)量級(jí)，相差在0.39%以?xún)?nèi)。在實(shí)際應(yīng)用過(guò)程中，可以選取任意鉸鏈鉸點(diǎn)進(jìn)行計(jì)算分析。

4 結(jié)語(yǔ)

對(duì)于高精度六自由度并聯(lián)機(jī)構(gòu)，鉸鏈的加工安裝誤差至關(guān)重要。然而位姿誤差與鉸鏈鉸點(diǎn)誤差關(guān)系具有非線性強(qiáng)耦合多變量等特點(diǎn)，在給定六自由度并聯(lián)機(jī)構(gòu)的六個(gè)位姿誤差時(shí)，無(wú)法直接求解出36 個(gè)鉸點(diǎn)誤差。文章基于靈敏度提供了一種鉸點(diǎn)誤差分配方法。該方法計(jì)算過(guò)程清晰，相對(duì)簡(jiǎn)單，計(jì)算量小，在高精度六自由度并聯(lián)機(jī)構(gòu)的鉸鏈加工與安裝中給出精度指導(dǎo)與依據(jù)。