基于核偏最小二乘法的濕法冶金萃取過程建模

陳 溥

(柳州鐵道職業技術學院，廣西 柳州 545616)

目前，國內外有關銅溶劑萃取過程中的建模研究較少，建立使用模型對于萃取過程中的自動控制有重要意義[1-5]。建立關鍵生產指標預測模型，對萃取過程的控制和優化至關重要，但影響過程操作的重要動力學傳質速率無法測量。研究提出了一種適用于銅萃取過程中的結合機理模型和數據模型的混合模型。該模型由參數未知(傳質速率)的機理模型和參數未知的數據預測模型組合而成。利用核偏最小二乘法(kernel partial least square，KPLS)建立傳質速率預測模型，通過仿真與BP(back propagation)神經網絡的混合模型進行對比分析。

1 銅溶劑萃取過程概述

銅萃取過程可分解為萃取、洗滌、反萃取3個階段[6-7]。

萃取階段：含有銅離子的水相與有機相混合，銅離子被萃入到有機相[8]。洗滌階段：負載有機相用洗滌劑洗滌，將夾帶的金屬離子洗出有機相。反萃取階段：用反萃取劑對洗滌后有機相進行反萃取，使銅離子返回水相。

影響銅溶劑萃取過程的因素有相比、溫度、水相pH、萃取劑濃度、被萃取金屬離子濃度等[9-10]。

2 混合建模

銅萃取過程機理模型的未知參數實際上無法測量，所以，提出了一種混合模型。該模型將機理模型和數據模型相結合，由參數(傳質速率)未知的機理模型和參數未知的數據預測模型組成[11]。用KPLS法分別建立數據預測模型。

2.1 動態機理模型

動態機理模型描述萃取過程中組分濃度隨時間的變化，是溶劑萃取過程控制系統的依據，有助于實現組分濃度優化控制。

在建立動態模型之前，對于多級逆流萃取過程做出以下假設：

1)兩相完全混合，并且僅在混合器中進行傳質；

2)兩相不混溶，澄清器沒有返混和逆流現象；

3)傳質系數、萃取平衡等溫線參數和效率參數不恒定，根據離線測量估算[12]；

4)萃取過程中兩相體積不變；

5)萃取過程中各組分濃度隨時間變化，是時間的函數。

根據物料平衡關系，建立第i階段萃取過程的動力學模型，見式(1)～(3)[13]。

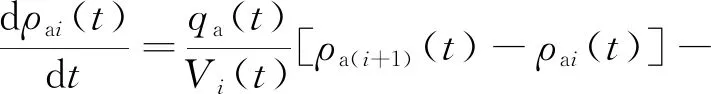
(1)

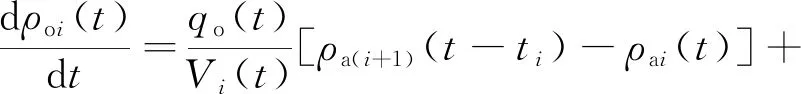
(2)

ρoi(t)=f(ρa(i+1)(t-ti),ρa(i+1)(t),qa(t),qo(t),A,B)。

(3)

式中：Vi—i級混合澄清器中混合相體積，L；qa、qo—水相、有機相流量，m3/h；ρa(i+1)為i+1級澄清器出口水相中Cu2+質量濃度，g/L；ρo(i-1)為i-1級澄清器出口的有機相Cu2+質量濃度，g/L；t、ti—萃取、滯后時間，h；Ki為第i級傳質系數，L/s；ρoi(t)-ρo*i(t)為傳質的驅動力，kN/m3；ρo*i為第i級達到平衡時有機相中Cu2+質量濃度(理想狀態)，g/L，與上層Cu2+進入水相的濃度、下一階段進入有機相的濃度、水相和有機相的流量、效率參數(α)和平衡萃取線常數A、B之間存在未知的函數關系，當i=N時，Ki[ρoi(t)-ρo*i(t)]為傳質速率，g/(L·h)。

用McCabe-Thiele圖計算平衡關系確定萃取級數，萃取部分理論平衡值根據水相和有機相中Cu2+及水相和有機相流量比確定。萃取平衡值x*計算公式[14]為

(4)

式中：a=-qa/qo；b=ρo(i-1)-aρa(i+1)，g/L。

α受有機相中試劑濃度和水相料液酸度影響。根據理論濃度平衡值x*(水相)和y*(有機相)、輸入的水相濃度和有機相中Cu2+質量濃度ρin及實際Cu2+質量濃度平衡值ρout估算每個萃取單元的萃取效率。見式(5)，該值接近于1[15]。

(5)

當萃取達到平衡時，萃取過程處于穩定狀態，見式(6)[16]：

q(tend)[ρin(tend)-ρout(tend)]-
KiV[ρout(tend)-ρ*out(tend)]=0，

(6)

一般來說，ρout(tend)-ρ*out(tend)非常小。用ε表示，ρout(t)-ρ*out(t)，導出傳質系數K，見式(7)[17]：

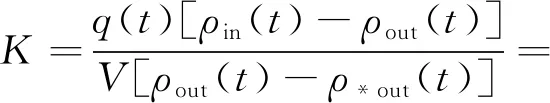
(7)

傳質系數受多種因素影響，如操作條件、反應器尺寸等。在交叉參考微反應器中，銅的傳質系數為31.12～214.34 L/s[18]；混合澄清器的K=50～400 L/s。

2.2 BP神經網絡模型

BP神經網絡有3層，輸入層、輸出層和隱藏層，每層有多個節點[19]。節點是神經元，神經元之間的連接線為權重。基本BP網絡如圖1所示。

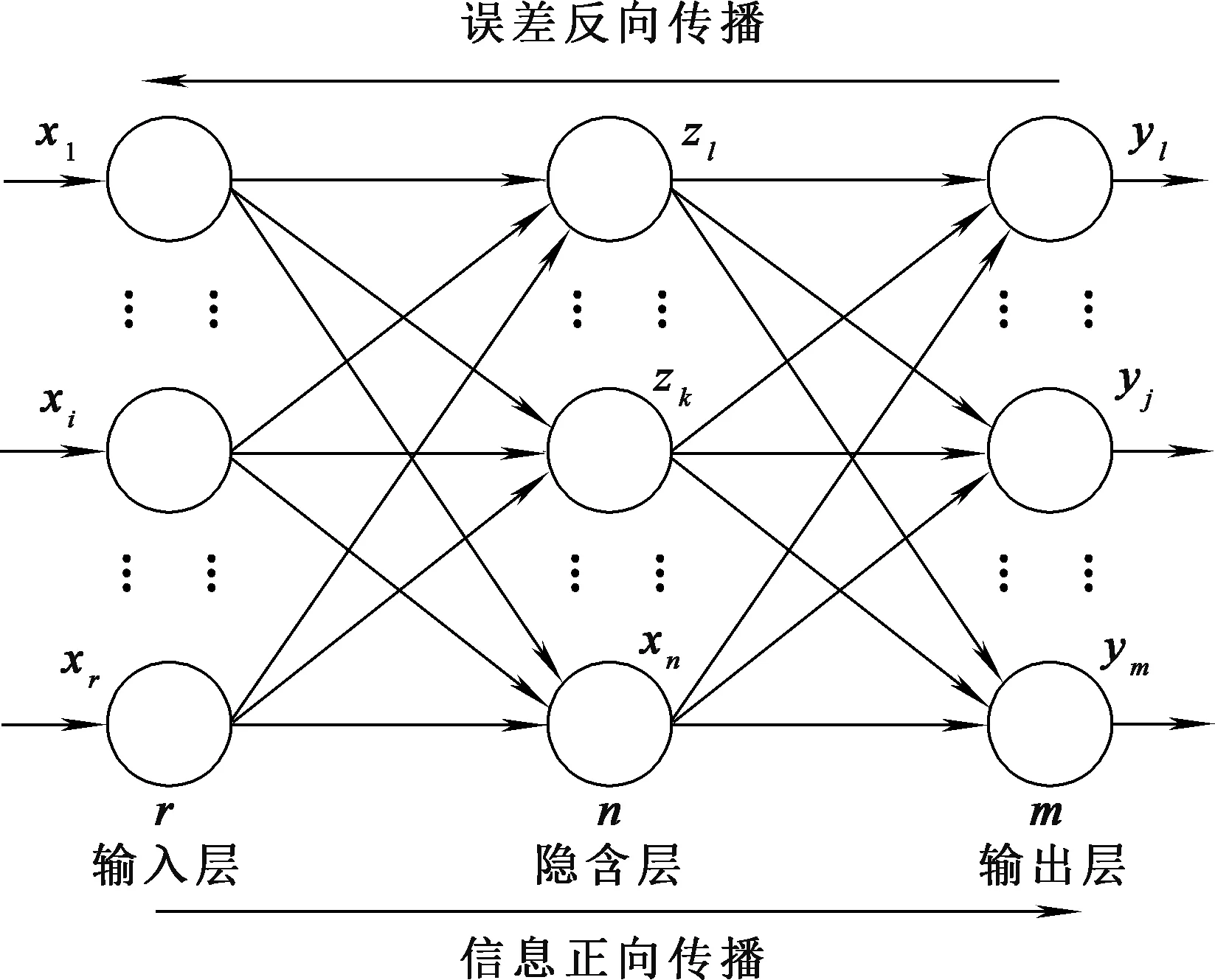
圖1 基本BP神經網絡模型

假設輸入層、輸出層、隱含層節點數分別為r、m、n；xi為輸入層i神經元的輸入值；zk、sk分別為隱含層第k個節點的輸出值和凈輸入值；yj、sj分別為輸出層j節點的實際輸出和凈輸入值；vik、wkj分別為輸入層i節點與隱含層k節點和隱含層k節點與輸出層j節點之間的連接權值。

正向傳輸過程中，輸出層和隱含層的輸出計算公式見(8)～(11)[20]。

zk=f(sk),k=1,2,……,n；

(8)

(9)

yj=f(sj)，j=1,2,……,m；

(10)

(11)

在式(8)～(11)中，選擇激勵函數f(x)=1/(1+e-x)，其導數為f’=f(1-f)。通常，誤差函數(也稱性能函數)E可以評估網絡性能，E越小，網絡性能越好。見式(12)，性能函數取均方誤差函數。

(12)

誤差反向傳播將誤差定義擴展到隱含層至輸入層，見式(13)。

(13)

標準BP算法用梯度下降法來調整層間權重，見式(14)、(15)。

(14)

(15)

如果η較大，則修正速度快且易振蕩；η較小時，則會導致網絡訓練時間長且收斂速度慢。η取值范圍為0.01～0.8。BP算法流程如圖2所示。

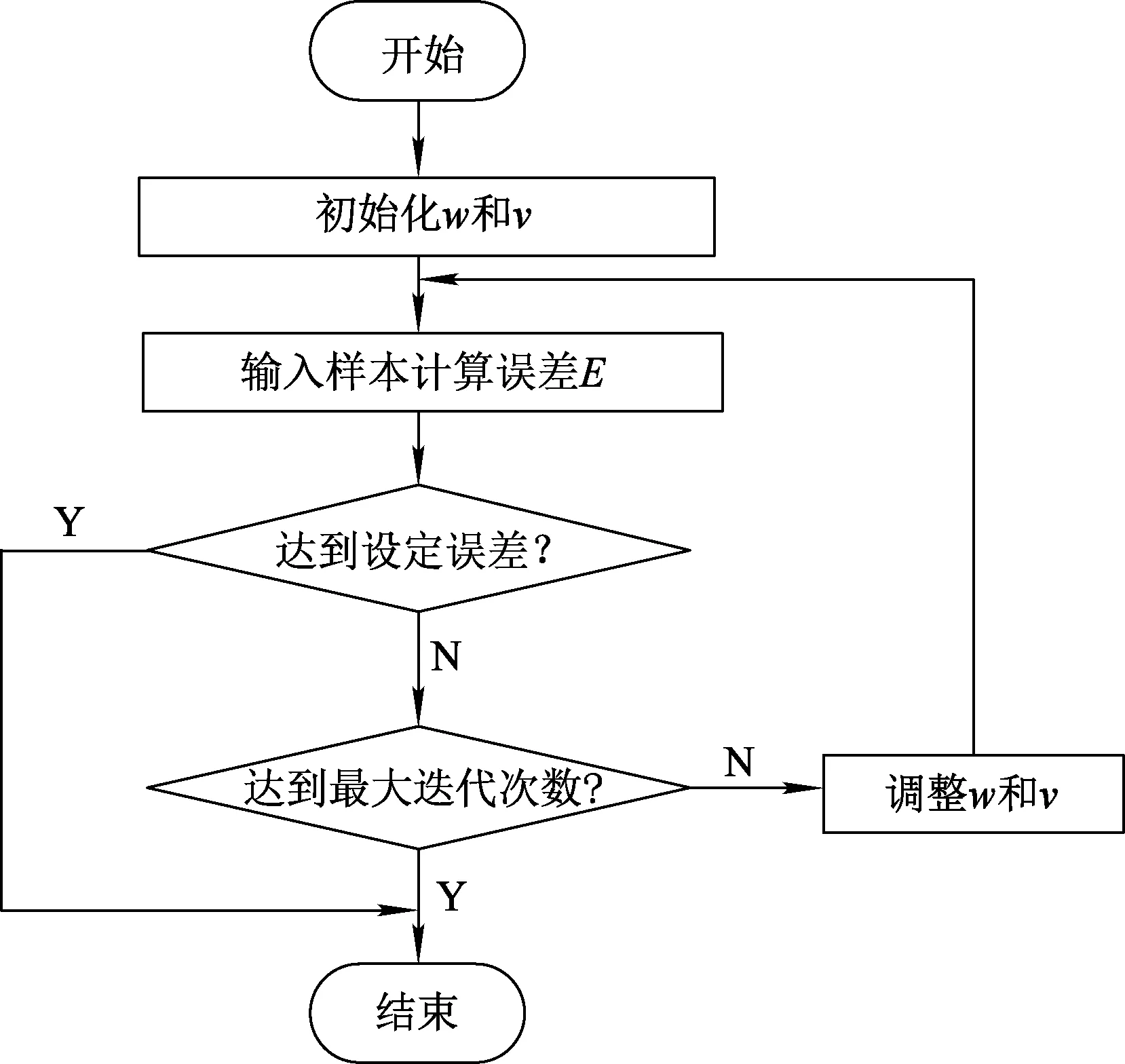
圖2 BP算法流程

2.3 核偏最小二乘法

偏最小二乘法(partial least square，PLS)是一種多元統計數據分析方法，可以解決普通多元回歸方法無法解決的許多問題[21]。偏最小二乘方法假定感興趣區域由一些潛在向量決定，這些向量是觀測值的線性組合。假設有向量個因變量{y1,y2,…,yq}和p個自變量{x1,x2,…,xp}，觀測n個樣本點。X={x1,x2,…,xp}為輸入變量的n×p矩陣；Y={y1,y2,…,yq}為相應輸出變量的(n×p)矩陣。

首先，從X和Y中提取得分向量t1和u1(t1為x1,x2,…,xp的線性組合，u1為y1,y2,…,yq的線性組合)，要求t1和u1盡可能代表矩陣X和Y。

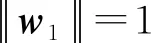
t1=Xw1；

(16)

u1=Yc1。

(17)

然后，建立X對t1、Y對u1的回歸方程，見式(18)(19)，且滿足式(20)。

X=t1p1T+E1；

(18)

Y=u1q1T+F1；

(19)

u1=f1(t1)+r1，

(20)

式中，p1、q1分別為得分向量對應的載荷向量。

殘差計算公式為(21)(22)。

E1=X-t1p1T；

(21)

F1=Y-u1q1T。

(22)

提取E1和F1得分向量，重復上述算法，直到得到第a個得分向量。殘差Ea和Fa幾乎沒有任何關鍵信息。

由于銅萃取過程的動力學反應為非線性，PLS算法無法解決該問題，因此引進核偏最小二乘法。該方法是在核希爾伯特空間(Reproducing Kemel Hilbert Space，RKHS)中建立的機器學習算法之一。用該方法建立模型的目的是最小化結構風險，即在(RKHS)中尋找最優模型。KPLS遵循PLS基本思想，它們的區別在于PLS建立從屬變量(y)和自變量(x)之間的相關性，而KPLS僅將自變量(x)投影到RKHS上，并且在RKHS中找到Ф(x)和y的相關性。KPLS的本質是在特征空間中構建PLS模型，有效地獲得非線性回歸模型。

同樣，觀測n個樣本，所謂“核技術”，實際上是Ф(xi)TФ(xj)=K(xi,xj)。可以看到，ФФT為所有映射的輸入數據點{Ф(xi)}n(i=1)之間交叉內積運算的核Gram矩陣K(n×n)，因此，可以用核函數來代替非線性映射。通常，當提取t分量后，矩陣見式(23)。

K←(I-ttT)K(I-ttT)=
K-ttTK-KttT+ttTKttT，

(23)

式中，I為n維單位矩陣。對PLS算法的非線性校正也可以得到類似的KPLS算法。修正的結果是從KYYT和YYT矩陣中提取得分向量t、u，步驟如下：

步驟1，隨機設定初始值u(可設定為u等于Y列中的任意一列)；

步驟2，根據t=ФФTu=Ku，計算得分向量；

步驟3，根據c=YTt計算系數向量；

步驟4，計算得分向量；

步驟5，重復2～5步，直到收斂；

步驟6，矩陣K和Y進行縮并，K←(I-ttT)K(I-ttT)，Y←Y-ttTY；

步驟7，返回步驟1，計算下一個t、u。

回歸系數矩陣B通過公式(24)計算得到，

B=ФTU(TTKU)-1TTY。

(24)

預測的訓練數據見式(25)，

Y*=ФB=TTTY。

(25)

KPLS算法流程如圖3所示。

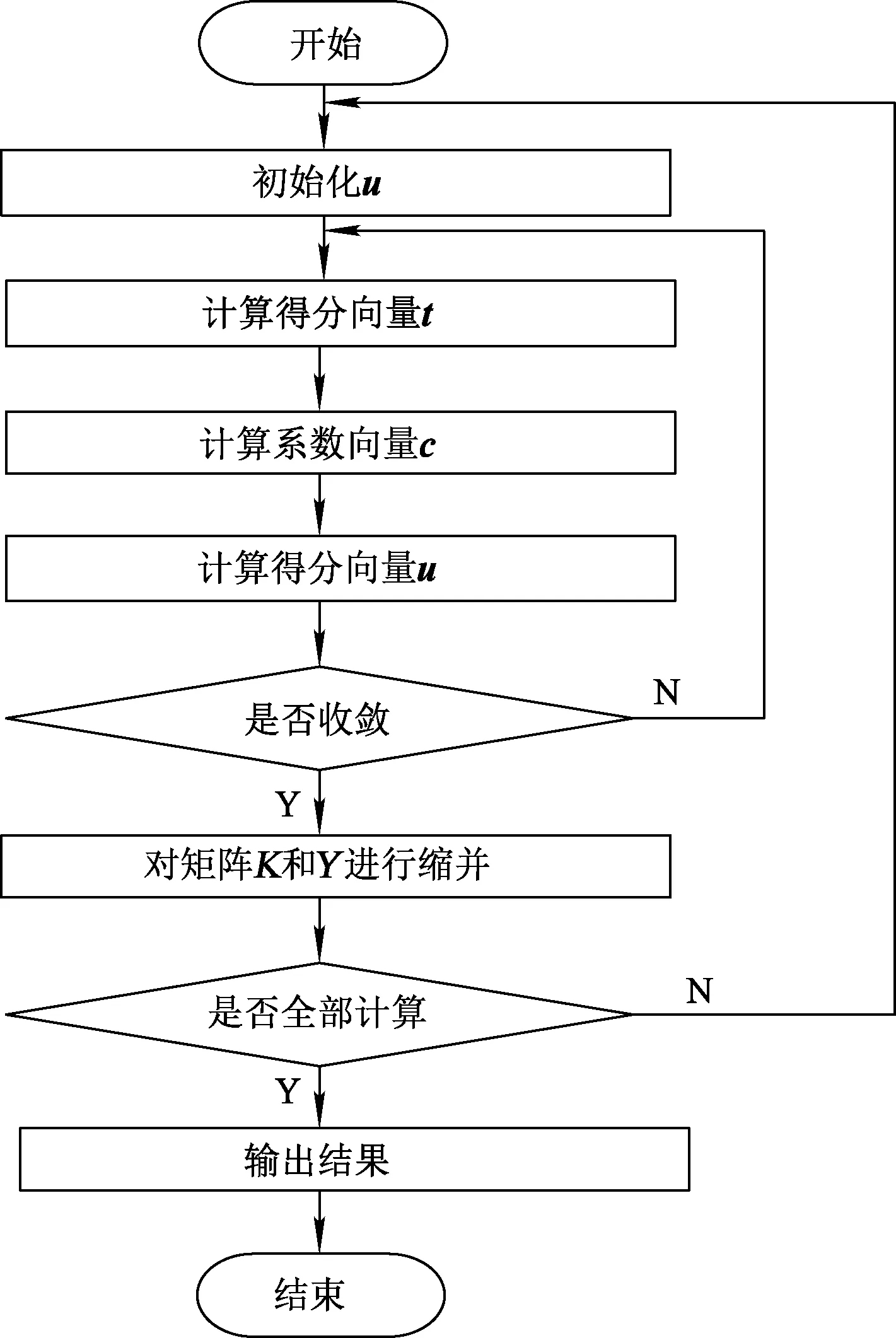
圖3 KPLS算法流程

3 仿真結果與分析

3.1 仿真參數

混合模型由參數未知(傳質速率)的機理模型和參數未知的數據預測模型組成。通過BP神經網絡和KPLS建立傳質速率預測模型，并與機理模型形成混合模型。數據模型是黑盒模型。在未知傳質速率模型結構和相關參數情況下，可以獲得傳質速率背后的過程變量之間的復雜關系，從而降低建模難度。在考慮過程的物理特性的同時，機理模型和數據模型組合有效地利用了相關的數據信息。這種混合模式具有很高的精度，適合于實際工業生產過程，為銅溶劑萃取工藝先進控制系統的開發和在線優化奠定了基礎。銅萃取混合模型如圖4所示。

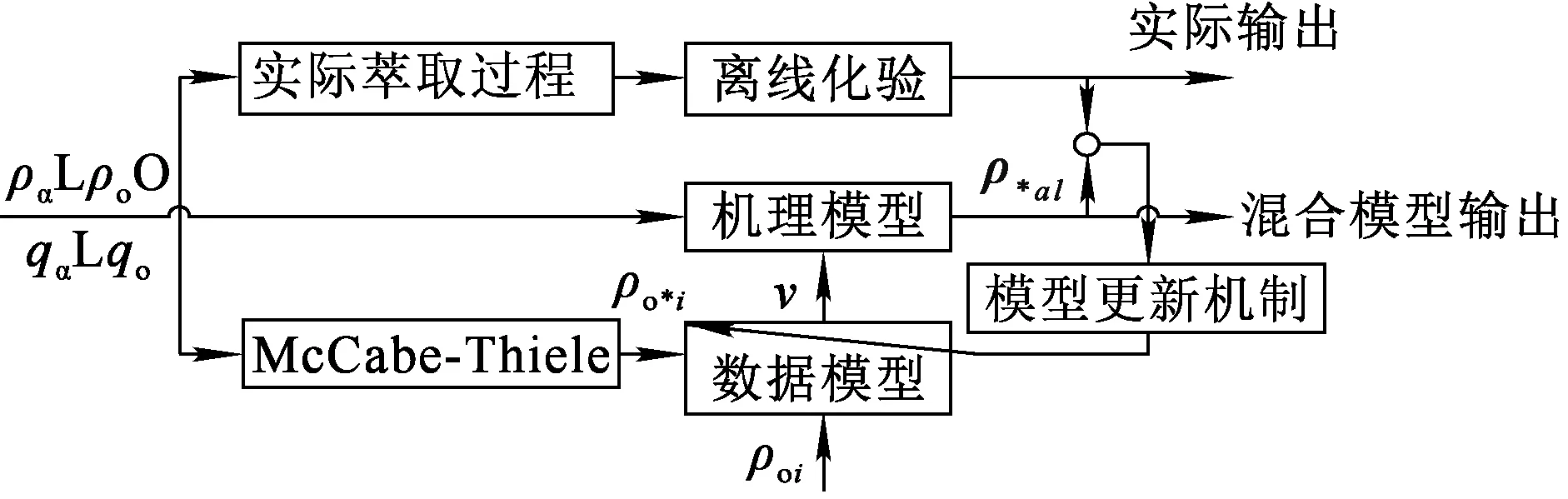
圖4 銅萃取過程混合模型

計算機為CPU i5-2450m，內存為8 Gb。仿真軟件為matlab2018。實驗室實際采集200組萃取過程穩態數據，100組用于訓練，100組用于測試。為了驗證和比較上述預測模型性能，利用以下3個性能指標對各算法性能進行評價。

1)均方根誤差(RMSE)

(26)

2)平均絕對誤差(MAE)

(27)

3)平均絕對百分比誤差(MAPE)

(28)

式中：xi和x*i分別為銅傳質速率實際值和預測值，M為預測樣品總數。

3.2 仿真分析

建立傳質速率黑箱模型，輸出傳質速率預測值。黑箱模型的輸入對應于傳輸速率估計值的影響因素。相同條件下，利用BP神經網絡和KPLS對傳輸速率進行建模。圖5為BP神經網絡及KPLS黑箱模型預測效果。可以看出：BP神經網絡的訓練效果良好，表明BP神經網絡黑箱模型具有準確的預測能力，非線性映射能力較好；但訓練中收斂速度較慢，并且在訓練集比較小時，容易發生過擬合；KPLS將初始輸入映射到高維特征空間，有效解決了非線性回歸問題。

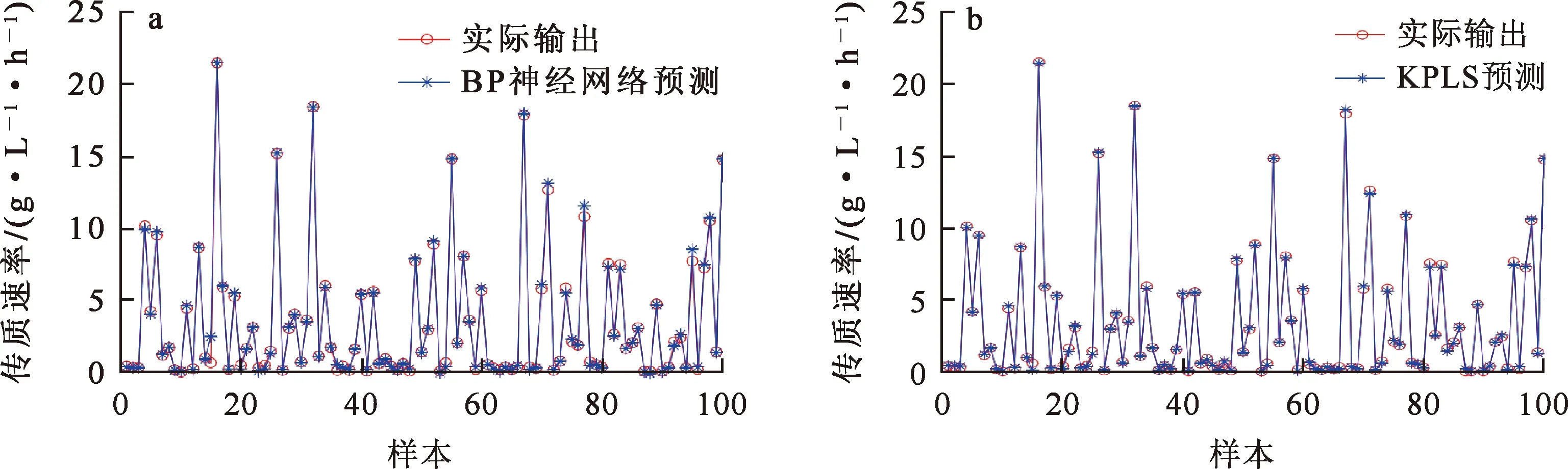
a—BP神經網絡預測模型；b—KPLS預測模型。圖5 黑箱預測結果

2個數據模型性能指標見表1。

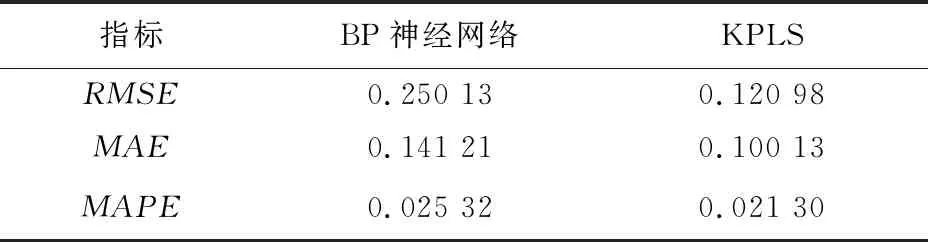
表1 BP神經網絡和KPLS數據模型預測性能指標

數據模型的正確性在混合模型構建中起重要作用。以上2種算法能夠準確預測傳質速率。由表1性能指標對比結果看出，KPLS方法效果較好。數據模型的準確性解決了傳質速率無法測量的問題，這為建立更接近實際過程的混合模型奠定了基礎。

對比單一模型和混合模型預測結果可以說明上述銅萃取過程混合模型的有效性，對比結果如圖6所示，各模型的性能指標見表2。

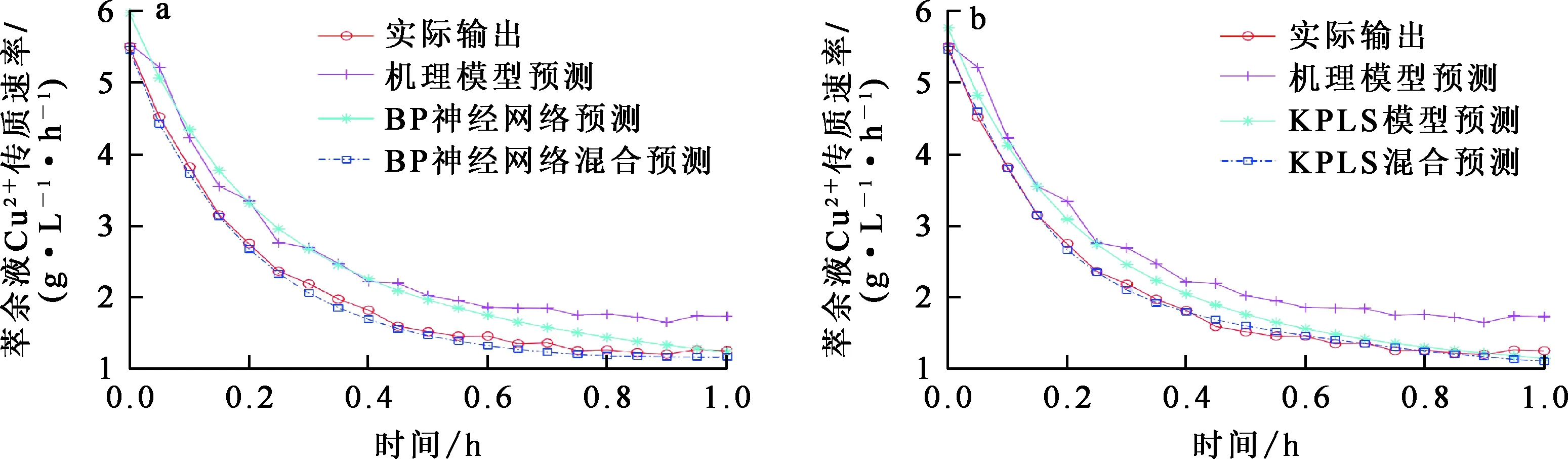
a—BP神經網絡；b—KPLS。

表2 單一模型和混合模型預測性能指標

由圖6看出：機理模型能夠很好預測過程趨勢；然而，由于萃取過程較為復雜，預測結果與實際值誤差較大；單一數據模型相對于機理模型需要考慮的因素更多，預測效果優于機理模型。由于數據模型不使用已知的經驗知識，僅依賴數據獲得輸入輸出之間的關系，純數據模型的泛化能力差，所以預測值和實際值誤差較大。混合模型將數據模型和機理模型優點相結合，精度較高，泛化能力強，有良好的預測效果，對銅溶液萃取工藝先進控制系統的開發和操作優化有一定參考性。基于KPLS的混合模型性能較優，RMSE為0.066 52，MAE為0.043 12，MAPE為0.019 82；對銅溶液萃取工藝先進控制系統的開發和操作優化有一定參考性。

4 結論

提出了一種混合模型，該模型由存在未知參數(傳質速率)的機理模型和未知參數的數據預測模型組成，通過數據模型預測機理模型的未知參數(傳質速率度)。混合模型性能的分析結果表明，基于KPLS的混合模型性能較優，均方根誤差、平均絕對誤差、平均絕對百分比誤差都較低，可作為銅萃取過程中自動控制系統開發的依據。考慮到實驗室設備和數據規模，建模方法還處于初級階段，還有待進一步完善。