Witt代數的r元組交換簇

姚裕豐, 張雅靜

（上海海事大學 數學系, 上海 201306）

0 引 言

設基域 F 是代數閉域, g 是 F 上的李代數,r∈Z≥2. 李代數 g 的r元組交換簇Cr(g) 是 g 中所有互相交換的r元組的集合, 即

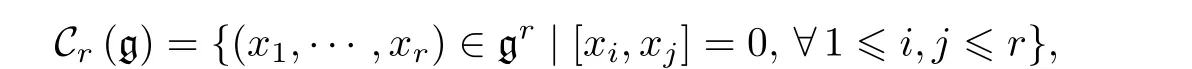
則Cr(g) 是 gr的閉子簇. 當 c harF=0 , g 是簡約李代數, 且r=2 時, Richardson[1]證明了C2(g) 是不可約簇. 此結論被Levi[2]推廣到了素特征域上簡約李代數的情形. 對于一般線性李代數 g ln, Gerstenhaber[3]證明了當n≥4 且r≥5 時,Cr(gln) 是可約的. 進一步, Kirillov和Neretin[4]證明了C4(gl4) 是可約的, 且對于任意的r≥1 ,Cr(gl2) 及Cr(gl3) 都是不可約的. Guralnick和Sethuraman[5]證明了當n≤10 時,C3(gln) 是不可約的, 而當n≥30 時,C3(gln) 是可約的.

不同于特征零情形, 特征大于5的代數閉域上有限維單李代數分為典型李代數和Cartan型李代數 (見文獻[6-7]). 作為非典型單李代數的第一個例子, 即Witt代數, 是由Witt于20世紀30年代首先發現的. Witt代數的2元組交換簇在文獻[8]中被確定, 同時還證明了該簇是可約簇且不是等維的,并給出了所有不可約分支. 本文在此基礎上進一步研究Witt代數的r元組交換簇.

1 預備知識

本文總假設基域 F 是特征p＞3 的代數閉域. 所有的代數(線性空間, 簇)都定義在 F 上.

設 A =F[X]/(Xp) 是域 F 上一個變量的截頭多項式代數, 其中 (Xp) 表示 F [X] 中由Xp生成的理想.為方便起見, 將X在 A 中的陪集也記為X, 則 A 有一組典范的線性基{1,X,···,Xp?1}. 設?是 A 上的線性算子, 定義如下:?Xi=iXi?1,0≤i≤p?1 . Witt代數W1即為 A 上的所有導子構成的李代數.

以下總假設 g =W1. 由文獻[9], g =spanF{Xi?|0≤i≤p?1}. 截頭多項式代數 A 上的自然 Z -階化

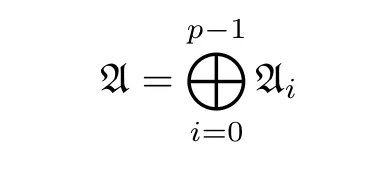
誘導出 g 的 Z -階化

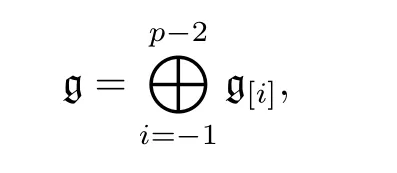
其中

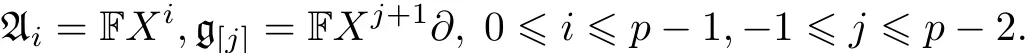
結合于此階化, 有以下自然濾過:

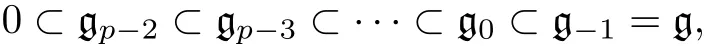
其中

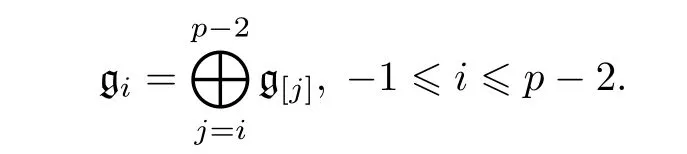
設G=Aut(g) 是 g 的 自 同 構 群, 則G是 一 個p?1 維 的 連 通 代 數 群, 且 L ie(G)=g0,σ(gi)=gi,?σ∈G,?1≤i≤p?2 . 對于 g 中的任意元素x, 它的中心化子 zg(x)={y∈g|[x,y]=0}是g的一個限制子代數. 需要以下關于 g 中元素中心化子的結構定理.

引理 1.1[8]設 g =W1是域 F 上的Witt代數,x∈gigi+1, 則

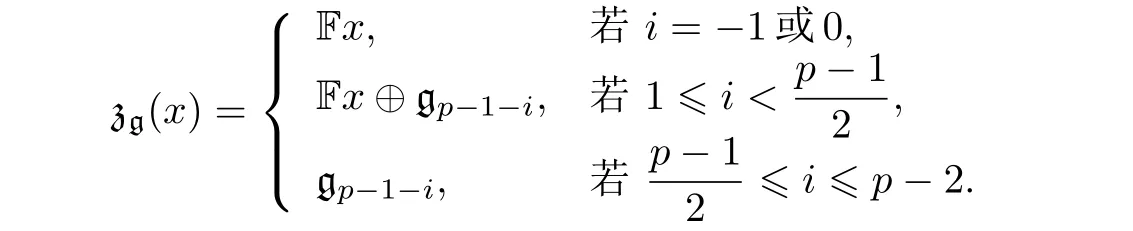
2 Witt代數的 r 元組交換簇

保持之前的記號, 特別地, g =W1是域 F 上的Witt代數,r∈Z≥2, g 的r元組交換簇Cr(g)={(x1,···,xr)∈gr|[xi,xj]=0,?1≤i,j≤r},則Cr(g) 是 gr的閉子簇, 且Cr(g) 在 g 的自同構群G的對角作用下不變, 即Cr(g) 是一個G-簇. 本章研究代數簇Cr(g) 的結構.

設

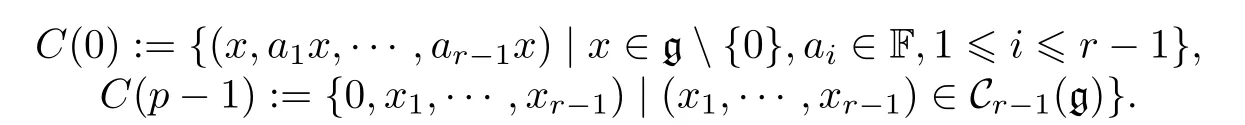
對于任意i∈{1,···,p?2}, 令

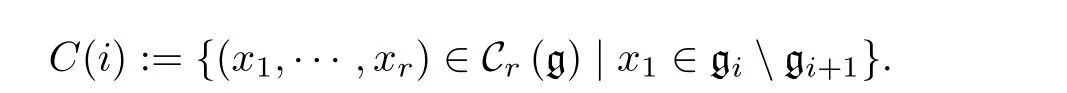
記C(i) 的閉包為 C (i) , 0 ≤i≤p?1 . 有下面簡單的引理.證 明 由C(0) 的定義知

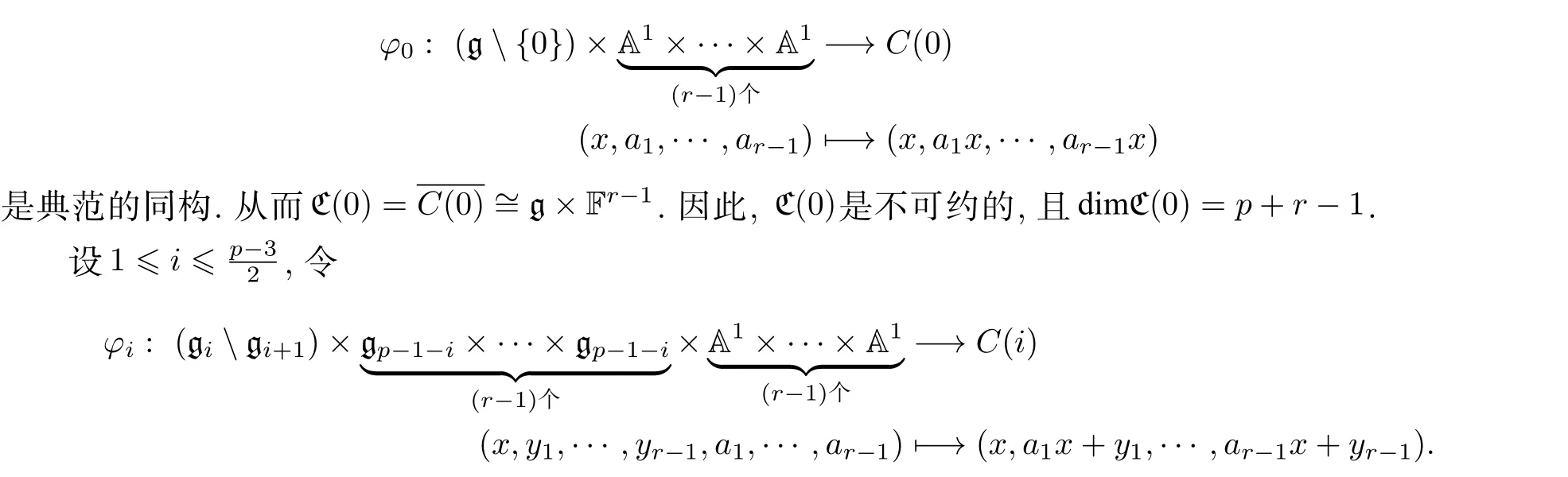
由引理 1.1 知φi是雙射. 從而, C (i) 是不可約的, 且

以下給出Witt代數r元組交換簇的結構定理.

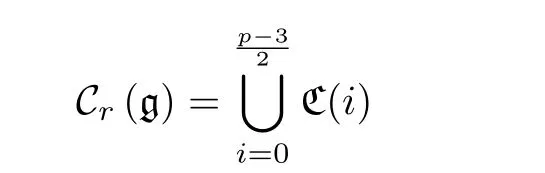
是Cr(g) 的不可約分支分解.

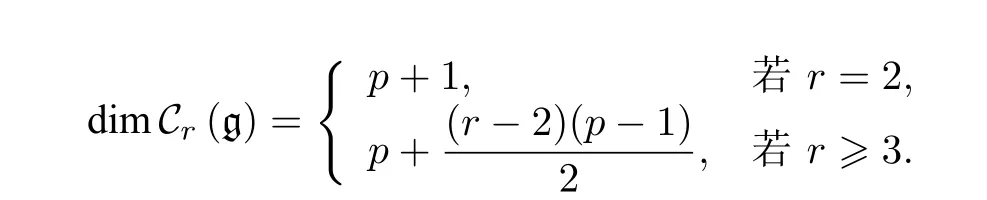
證 明 分以下幾步證明.

第1步 按如下方式定義GLr(F) 在 gr上的作用:

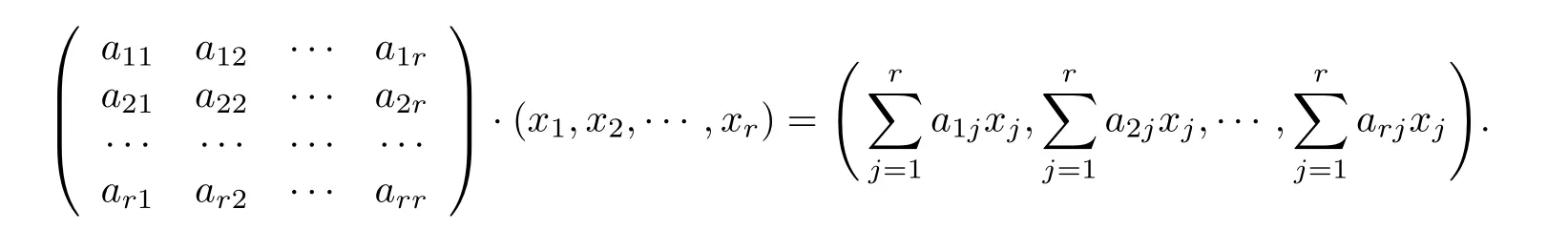
由Cr(g) 的定義易知Cr(g) 是 gr的GLr(F) -子簇. 由于GLr(F) 是連通代數群, 根據文獻[10]中的命題8.2知Cr(g) 的每個不可約分支在GLr(F) 作用下不變. 特別地, 對于任意 1 ≤i＜j≤r,Cr(g) 的每個不可約分支在以下對合作用下不變:

第2步 設

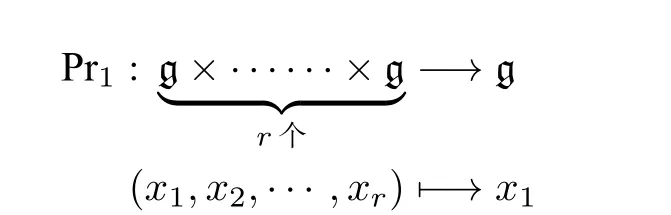
是典范的投射, 則 P r1(C(i))=gigi+1,1≤i≤p?2 , 而 P r1(C(0))=g , P r1(C(p?1))=0 . 因此,

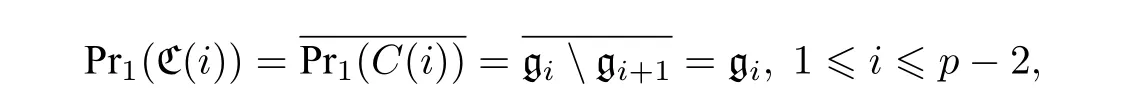
且

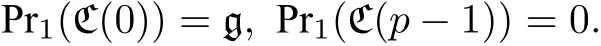
第3步 以下對r用數學歸納法證明定理的結論.

當r=2 時, 由 于C(?1):={(x,ax)|x∈g?1g0}?C(0) , 從而 C (?1):=C(?1)?C(0) . 由 引理2.2及文獻[8]中的定理1得到 C (?1)=C(0) . 因此, 由文獻[8]中的定理1知本定理當r=2 時成立.

以下假設r＞2 , 且本定理結論對r?1 成立. 設

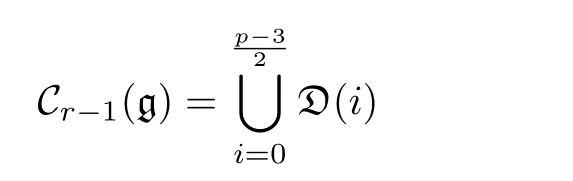
是Cr?1(g) 的不可約分支分解, 則

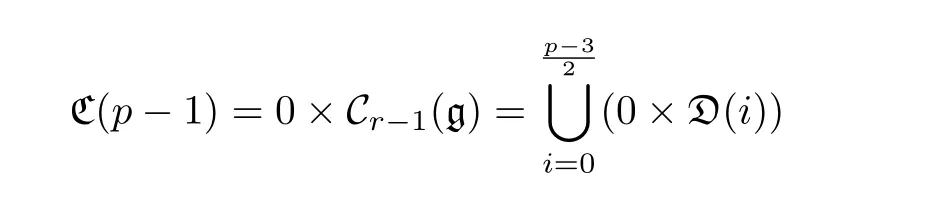
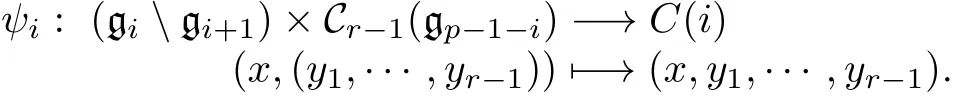
由引理1.1知ψi是同構. 從而 C (i)=gi×Cr?1(gp?1?i) . 設

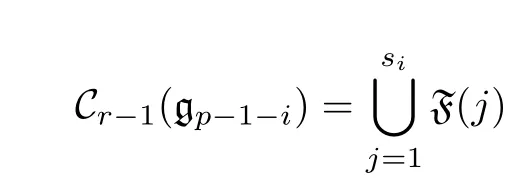
是Cr?1(gp?1?i) 的不可約分支分解, 其中si是Cr?1(gp?1?i) 的不可約分支的個數, 則

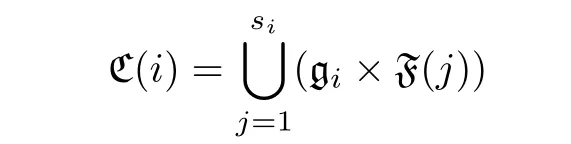
從而

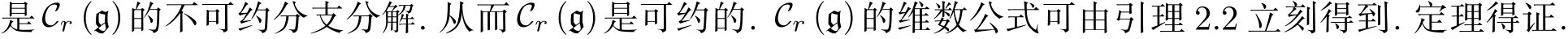
從定理2.1可得到下面的推論.

推論 2.1 設g =W1是特征p＞3 的代數閉域上的Witt代數,r∈Z≥2, 則 g 的r元組交換簇Cr(g)既不是正規的, 也不是Cohen-Macaulay.

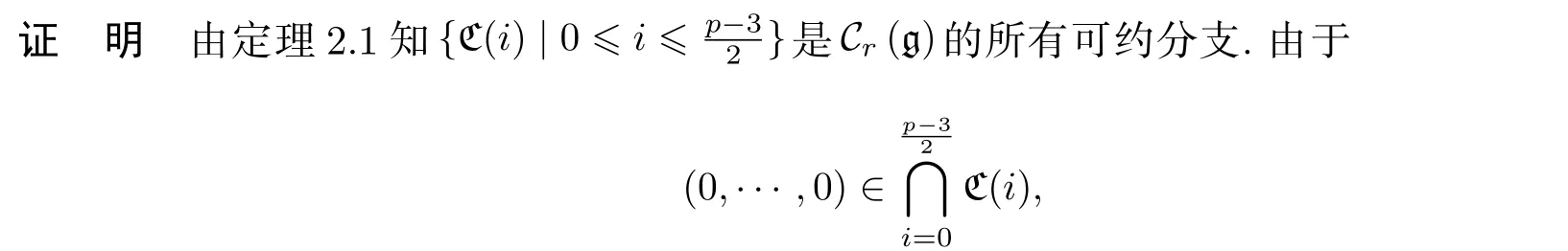
因此，根據文獻[11]中的注記17.1.3知Cr(g) 不是正規的. 進一步, 由定理2.1和引理2.2知Cr(g) 不是等維的, 從而不是Cohen-Macaulay.

注記 2.1 (1) 本文得到的關于Witt代數的r元組交換簇Cr(g) 的性質與典型李代數 g l2,sl2情形的性質截然不同. Ngo[12]得到當 L =gl2或 s l2時, L 的r元組交換簇Cr(L) 是不可約的、正規的、Cohen-Macaulay.

(2) 本文基域 F 的特征p＞3 這一限制條件是必需的. 當p=3 時, Witt代數W1同構于典型李代數sl2.

(3) 對于秩n的Witt代數Wn的r元組交換簇Cr(Wn) 的結構有待進一步研究.