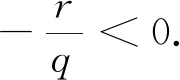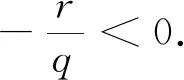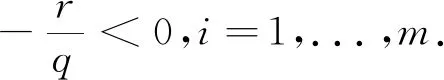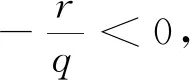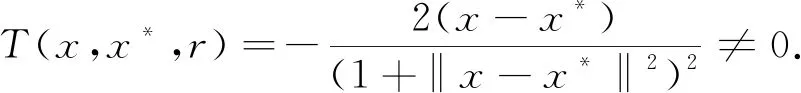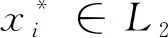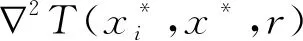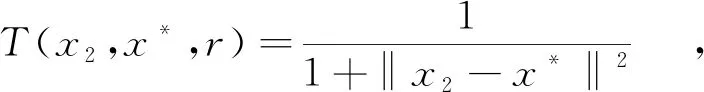含有不等式約束的全局優化問題的一種新的輔助函數法

王 倩

(四川文理學院 教務處，四川 達州 635000)

無約束的或者箱子集約束的全局優化問題有很多學者已經在不斷研究與改進，如文獻.[1-7]其中打洞函數法最早是于1985年在文獻[2]中提出的，其打洞函數為:

該方法要求f(x)在X上二次連續可微，并且假設函數f(x)只有有限個孤立的極小點.

后來，Ge.R.P在文獻[3]中提出了另一類求解一般非線性規劃問題的全局最優解的輔助函數法：填充函數法.文獻[3]中給出填充函數的基本思想是：通過極小化填充函數跳出當前的局部極小點，因而找到一個目標函數值比當前函數值更小的點，循環運算直至找到全局極小點.因該填充函數受到指數項的影響，會找到假的平穩點，因此丟失目標函數的全局最優解.

后來很多學者對其做了改進工作，如文獻.[4-8]特別在文獻[8]中提出的新的輔助函數法，無論在理論性質還是數值試驗結果上，較之前的輔助函數都有非常突出的優越性.然而文獻[8]中提出的新輔助函數法只是用于求解一般無約束的全局優化問題.而對于有約束的全局優化問題的研究，特別是含有不等式約束的全局優化問題的研究，是非常具有現實意義和研究價值的.在文獻[1]中Wu Z.Y.等提出了一種求解含有不等式約束的全局最優解的輔助函數法，其在理論性質和數值試驗結果上都有非常突出的優越性，但其不能保證平穩點函數的局部極小點是原問題的局部極小點，所以每次求解平穩點函數的局部極小點以后，還需要重新求解原問題的局部極小點.本文結合文獻，[1],[8]提出了一種新的改進填充函數法，用于求解含有不等式約束的一般非線性規劃問題的全局最優解.

新的改進填充函數及其性質

本文考慮如下問題(P)[1]

其中，f(x)和gi(x)在Rn→R上連續可微，i=1,...,m,.

假設1f(x)滿足強制性條件：當‖x‖→+∞時，f(x)→+∞.

假設2 問題(P)的局部極小值的個數為有限個.

令

S={x∈X|gi(x)≤0,i=1,...,m},

S0={x∈intX|gi(x)<0,i=1,...,m}.(2)

假設3S0為非空集，clS0=S.

本文假設x*為當前原問題(P)的局部極小點.

定義1 函數T(x,x*,r)稱為含有不等式約束全局優化問題(P)的改進填充函數，如果T(x,x*,r)滿足如下條件：

1)對任意的x∈S，00，T(x,x*,r)=0?f(x)-f(x*)+r=0;

2)設x*是f(x)的一個局部極小點，則?q>0，對任意的0

3)對任意的00， 則?T(x,x*,r)≠0;

4)對任意的x∈L2={x|f(x)

5)對任意的x1,x2∈S0，若f(x1)≥f(x*)，f(x2)≥f(x*)，則‖x2-x*‖>‖x1-x*‖當且僅當T(x2,x*,r)

下面給出一種改進的填充函數

其中00，φr(t)和ψr(t)具有如下的形式：

很容易驗證φr(t)≥0，ψr(t)≥0，且連續可微.

下面的定理表明，當參數r，q滿足某些條件時，本文構造的輔助函數T(x,x*,r)滿足定義1給出的改進填充函數的定義.

定理1 對任意的x∈S，00，T(x,x*,r)=0?f(x)-f(x*)+r=0.

證明：必要性(?)

充分性(?)

因為f(x)-f(x*)+r=0，所以φr(f(x)-f(x*)+r)=0.對任意的0≤r<1，?q>0，

證畢

定理2 設x*是f(x)的一個局部極小點，則?q>0，對任意的0

證明：因為x*是一個局部極小點，則?δ>0，對?x∈ο(x*,δ)∩S0，有f(x)≥f(x*)，

所以f(x)-f(x*)+r≥0+r>0,

故T(x*,x*,r)>T(x,x*,r)，即x*是T(x,x*,r)的一個嚴格局部極大點. 證畢

定理3 對任意的00， 則?T(x,x*,r)≠0;

證明：由(3)式知

定理4 對任意的x∈L2={x|f(x)

證明：當f(x)0，使得f(x)-f(x*)<-r，有

f(x)-f(x*)+r<0，則有T(x,x*,r)=r(f(x)-f(x*)+r)3.

這時?T(x,x*,r)=3r·(f(x)-f(x*)+r)2?f(x)，因為f(x)-f(x*)+r<0，

所以?T(x,x*,r)與?f(x)同號，從而T(x,x*,r)和f(x)的單調性保持一致.

T(x,x*,r)的局部極小點. 證畢

定理5 對任意的x1,x2∈S0，若f(x1)≥f(x*)，f(x2)≥f(x*)，則‖x2-x*‖>‖x1-x*‖當且僅當T(x2,x*,r)

證明：因為對任意的x1，x2∈S0，若f(x1)≥f(x*)，f(x2)≥f(x*)，則

所以，‖x2-x*‖>‖x1-x*‖當且僅當T(x2,x*,r)

定理5保證了輔助函數在極小化搜索過程中，不會再回到原來極小點所在的盆谷中.

由以上的定理及定義1可以得到，當參數r和q滿足一定條件時，函數T(x,x*,r)是點x*處的新的改進填充函數.

由于文獻[8]中的輔助函數算法在數值實驗結果中有較為突出的有效性，因此，可借鑒該算法進行推廣，在數值試驗中可進行有效性的檢測.