基于MPSO-SVM非線性氨氮傳感器的數據補償
韓 劍,莫德清,汪 楠
(1.桂林電子科技大學信息科技學院, 廣西 桂林 541004; 2.桂林電子科技大學 生命與環境科學學院, 廣西 桂林 541004)
目前,氨氮傳感器主要是利用電化學原理,通過測量電勢,建立電勢與氨氮濃度之間的關系式獲得氨氮濃度。對于溶液中pH值和溫度的影響,一般采用電化學中的能斯特方程進行計算[1]。 但是受氨氮傳感器自身因素以及測量環境等影響, 傳感器數據輸出呈現非線性特點。 因此, 直接得到的測量數據并不可靠, 有必要對氨氮傳感器測量的數據進行校正。
鑒于此,本文將改進的粒子群參數尋優算法(MPSO-SVM)引入到氨氮傳感器模型中[2],以降低氨氮傳感器的測量誤差,建立適應性良好的補償模型。通過取不同梯度濃度值, 分別測量約270組數據,建立支持向量回歸校正模型[3],進行數據校正,本質上解決非線性回歸問題。
1 支持向量機回歸模型
在氨氮傳感器測量過程中考慮實際測量環境復雜多樣,測量結果受多種因素的影響,因此將氨氮的測量校正過程看作是求解一個多元非線性回歸問題。
首先將氨氮傳感器測量輸入輸出之間的關系抽象成模型
y=f(t,P,x1,x2,…,xi),
(1)
式中:x為傳感器輸入非目標參量;t和P分別表示溫度值和pH值;y為傳感器輸出量;f為輸入與輸出之間的映射關系。
實際應用中,氨氮傳感器得到一個實際測量值,通過數據校正過程利用其反函數來建立關系式
(t,P)=f-1(x1,x2,…,xi),
(2)
再利用支持向量機來逼近式(2)描述的非線性函數問題,以此來消除氨氮測量過程中對目標參量的影響[4]。 最終,將輸入的測試數據通過回歸模型進行預測獲得更準確的結果。
為了解決本質上非線性回歸問題,按圖1所示模型(X表示傳感器采集的原始數據,一般是多個參數;Y是基于核方法的支持向量機模型補償后的輸出數據,對于此模型而言,Y表示最終的氨氮傳感器測量值),利用SVM核函數,將氨氮傳感器的影響因素(包括溶液溫度、pH值以及數據采集電路自身的影響)作為輸入數據, 建立回歸校正模型。 引入非線性映射φ,把樣本空間η映射到一個高維(甚至是無窮維)的特征空間H(Hilbert空間),在高維空間中進行線性回歸運算,從而獲得原輸入樣本空間的非線性回歸效果,以達到氨氮傳感器非線性補償效果[5]。

圖1 支持向量回歸機數據補償模型框圖Fig.1 Support vector regression data compensation model block diagram
2 基于改進粒子群的支持向量機參數優化過程
由于傳感器實際測量的數值具有非線性的特性,因此核函數采用同樣為非線性的Gauss函數核(也稱作徑向基核,radial basis function, RBF)[6]:
K(X,Y)=exp(-g‖xi-xj‖2)
(3)
其中,g為核函數的參數,g>0, 默認為1/k(定義k為輸入數據的屬性的數目), 調整g可改善支持向量機的預測準確度[7]。
2.1 MPSO-SVM優化參數設置
利用改進粒子群(MPSO)對支持向量機(SVM)的參數進行搜索尋優, 在求解支持向量機模型的過程中,懲罰因子C和RBF的核參數g取值恰當與否直接決定了模型的性能:C太大或g太小易造成過度學習, 導致模型泛化,性能變差;C太小或g太大則易產生欠學習現象,即確定參數C和g本質上是一個動態尋優的過程[8]。
利用libsvm工具箱,通過對MPSO-SVM訓練, 3個待優化的MPSO-SVM參數:懲罰系數C、徑向基核函數參數g、不敏感損失函數系數ε[9](分別用d、g、p表示),得到最佳參數為dbest、gbest、pbest。將MPSO-SVM的3個參數(d,g,p)作為MPSO中粒子的位置xi,可以把支持向量機的參數尋優問題轉化為利用MPSO求三維空間中的最優解問題。另外需定義一個性能指標作為目標函數,也即MPSO中用于評價群體中各粒子的適應度。表1列出了粒子群算法的基本參數范圍設定情況。

表1 改進粒子群算法的參數范圍設置Table 1 Parameter range setting of improved particleswarm optimization
2.2基于MPSO-SVM的計算流程
首先對根據標準溶液測量得到的數據進行歸一化,再將處理后的數據作為支持向量機回歸模型的輸入,進行目標參數的計算,將最終滿足適應度條件的計算結果反歸一化即可得到目標參數的值,若達不到相應精度則繼續利用MPSO尋優重新訓練模型[10]。圖2為改進粒子群算法進行SVM參數優化計算的詳細流程圖。

圖2 MPSO-SVM參數優化計算流程Fig.2 Parameters optimization calculation process based on MPSO-SVM
3 數據采集與分析
3.1 氨氮檢測系統
氨氮檢測系統主要由電化學氨氮傳感器和數據采集模塊組成,傳感器直接檢測的信號比較微弱,數據采集模塊主要是對電化學氨氮傳感器信號進行放大、濾波、采樣等一系列操作, 實現由微處理器進行初步數據處理,以及與上位機進行交互等功能,圖3為氨氮檢測系統的主要構成部分的示意框圖。

圖3氨氮檢測系統主要結構框圖Fig.3 Main structure block diagram of ammonia detection system
3.2 數據采集及預處理
首先對幾種不同標準溶液分別利用氨氮檢測系統進行測量,然后分別采用遞推平均濾波、IIR數字濾波和卡爾曼濾波3種濾波方式在微處理器里進行數字濾波操作,測量數據包括:當前溶液溫度(℃)、利用氨氮傳感器采集對應濃度待測溶液的輸出電壓采樣值 (16位AD轉換器的實際數據)、經過濾波器后的電壓(V)、溶液的pH值,經過3種濾波方法的濾波值,每次分別得到約270組測量數據。部分數據見表2。

表2 數據采集模塊采集的部分數據Table 2 Partial data collected by data collection module
采集模塊分別采集了3種不同濃度溶液的測量數據,并對3種濾波方法進行了比較(圖4)。可知,經過數據采集模塊進行電壓放大后測得的電壓在±20 mV波動,IIR濾波器和卡爾曼濾波都有一定的時延,遞推平均濾波方法對應的數據波動更大,其中卡爾曼濾波效果最好。

圖4 3種不同濾波方法電壓比較Fig.4 Voltage comparison of three different filtering methods
3.3 氨氮傳感器的MPSO-SVM函數模型及補償方法
為降低氨氮傳感器的測量誤差,建立適應性較好的補償模型,將適用于非線性模型回歸分析的MPSO-SVM算法引入到氨氮傳感器模型中[9], 以《水質 氨氮的測定 納氏試劑分光光度法》(HJ 535—2009)監測的實際值為參照標準,具體如下:在各溫度下分別采集不同濃度的多組離散數據作為訓練樣本,把溫度t、pH值P和氨氮檢測系統采集的電壓U0作為MPSO-SVM算法的輸入量,樣本集D為
D={(x1,y1),(x2,y2),…,(xi,yi)},
i=1,2,…,n。
(5)
分別采用Grid-SVM、MPSO-SVM和GA-SVM 3種方法對氨氮傳感器模型參數尋優過程進行了比較,MPSO-SVM和GA-SVM分別對種群迭代100次,默認采用3-折交叉驗證方法檢驗準確度。按照圖2所述的步驟利用MPSO-SVM求解出SVM的最優參數,并且記錄尋優過程中的最佳適應度值和平均適應度值,再利用另外兩種方法計算出SVM的最優參數,比較3種方法的尋優效果以及數據補償效果。圖5a、b分別顯示了MPSO-SVM、GA-SVM在尋優迭代過程中最佳適應度值和平均適應度值與迭代次數的關系;圖5c顯示了Grid-SVM在尋優過程中適應度值與網格搜索次數的關系(由于網格搜索算法的特點, 隨著網格劃分的增加, 算法計算復雜度呈指數式增長, 這里顯示的只是前600次搜索產生的結果)。

圖5 MPSO-SVM、GA-SVM、Grid-SVM方法對參數尋優Fig.5 Parameter optimization of MPSO-SVM,GA-SVMand Grid-SVM
觀察3種模型訓練過程趨勢圖(圖5),對3種方法回歸效果進行比較(表3),可以看出,利用MPSO-SVM算法可以很快地收斂,并且回歸效果也是最佳的;GA-SVM能夠得到較好的回歸效果,但是遺傳算法本身需要大量的樣本訓練,因此,迭代100次之后算法還未能很好收斂,而且也有一定的計算復雜度;Grid-SVM算法取決于目標參量的個數以及網格劃分規模,在本文中計算量很大,而且回歸效果不如前兩種方法。

表3 MPSO-SVM、GA-SVM和Grid-SVM方法回歸效果比較Table 3 Regression effects of MPSO-SVM,GA-SVM and Grid-SVM
比較不同非線性回歸方法對氨氮測量數據的誤差補償效果。 圖6顯示了采用四階多項式回歸擬合與MPSO-SVM算法對比回歸曲線。可以發現,MPSO-SVM算法補償得到的數據更加接近原始數據,而多項式回歸方法部分數據偏離原始數據較大,表明MPSO-SVM算法回歸效果最佳。
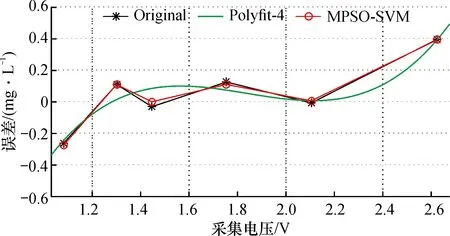
圖6 不同非線性回歸方法對氨氮測量數據誤差補償效果對比Fig.6 Comparison of different non-linear regression methods on error compensation effects of ammonia nitrogen monitoring data
3.4 測量氨氮濃度誤差分析
以納氏試劑-分光光度計國標法監測的實際值為參照標準,測量6組不同濃度的數據作為對比,重復兩次測量,表4顯示了采用MPSO-SVM算法模型對測量數據的進行補償以及誤差分析的結果。在傳感器的有效測量范圍內,最大相對誤差在±3%左右,表現出良好的補償效果,并且由于支持向量機小樣本訓練的特點,因此該數據補償算法具有一定的泛化能力。

表4 氨氮濃度監測值、MPSO-SVM算法數據補償結果以及誤差分析Table 4 Monitoring value of ammonia nitrogen concentration,MPSO-SVM algorithm data compensation results and error analysis
4 結 論
通過分析氨氮傳感器在測量過程中受多種因素的影響, 采用了改進粒子群支持向量機的數據補償方法, 利用改進的粒子群算法支持向量機建立數據補償模型, 與基于網格搜索支持向量機和基于遺傳算法支持向量機[11]相比, 改進粒子群支持向量機的數據補償方法效果更佳,算法更容易收斂, 也滿足一定的測量精度, 氨氣敏電極傳感器測量值與真實的相對誤差在±3%內, 系統測試體現出較好的穩定性,表現出良好的補償效果, 且由于支持向量機小樣本訓練的特點, 該數據補償算法具有一定的泛化能力, 整個嵌入式開發系統還可以擴展多參數測量系統, 以本地主機作為監測服務器, 提供檢測數據對外發布接口, 方便進行數據對外公開。本研究有望用于市政污水處理的過程監控。

