2020年高考北京卷第20題的拓展探究

福建省莆田第十中學 (351146) 林清霞

1.提出問題

2.特殊探路

3.猜測論證

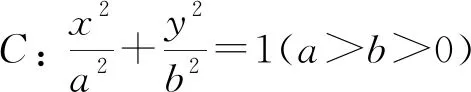
對于雙曲線、拋物線，有類似的結論.

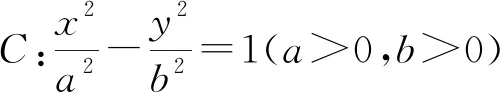
下面只給出結論3.1的證明.

4.逆向拓展

結論1.1的逆命題成立嗎？經過探究可得：

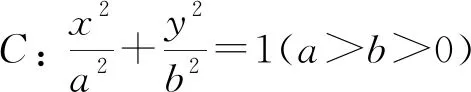
類似地，可得結論2.1、3.1的逆命題：

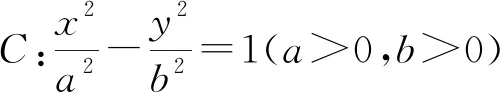
以上通過對一道高考試題的拓展探究，得到了橢圓、雙曲線和拋物線的一類性質，揭示了問題的本質和規(guī)律，使學生經歷了在教師指導下的“提出問題—特殊引路—猜測論證—逆向拓展”的探究過程，這無疑有助于學生對圓錐曲線問題的深度學習，有助于培養(yǎng)和提升學生的探究能力和數學學科核心素養(yǎng).這正如《普通高中數學課程標準》(2017)所指出：“圍繞某個具體的數學問題，發(fā)現和提出有意義的數學問題，猜測合理的數學結論，提出解決問題的思路和方案，通過自主探索、合作研究論證數學結論”，“在問題解決的過程中，理解數學內容的本質，促進學生數學學科核心素養(yǎng)的形成和發(fā)展”.