“點全?線聯?面融”式教材解讀與實踐思考

張文珠

[摘 要]教材解讀為教學素材與素養目標之間勾畫實踐路徑.教師可利用“點全·線聯·面融”式的解讀方法對教材進行單元整體分析及知識整合，讓零散的知識變得立體有層次、系統有框架，幫助學生構建完整的知識體系，綜合提高學生的數學素養.

[關鍵詞]“點全·線聯·面融”;教材解讀;教材素材

[中圖分類號]??? G633.6??????? [文獻標識碼]??? A??????? [文章編號]??? 1674-6058（2021）02-0025-02

高效的課堂教學實踐取決于有效的教學設計，有效的教學設計有賴于教材的深度解讀.教材解讀為教學素材與素養目標之間勾畫實踐路徑.教師可利用“點全·線聯·面融”式的解讀方法對教材進行單元整體分析及知識整合，讓零散的知識變得立體有層次、系統有框架，幫助學生構建完整的知識體系，綜合提高學生的數學素養.筆者以蘇科版七年級數學下冊“有理數的乘方”為例，談談對“點全·線聯·面融”式教材解讀與實踐的思考.

一、教材素材

“有理數的乘方”課時的素材分為兩類， 即“顯性”的知識素材和“隱性”的素養素材.

在知識素材層面，學生小學階段已學習了正數的平方、立方運算，能用于解決正方形的面積、立方體的體積等相關問題.初中階段，學生剛學完有理數的加、減、乘、除運算，將這些已有知識進行整合、再理解，能為本課時的教學提供很好的知識素材.

在素養素材層面，學生已初步具有對數學問題進行自主探究、合作交流的意識與能力.當學生遇到現實生活中的數學問題時，他們潛意識中會應用數學的知識來解決.教師要充分利用學生這一特點，引導學生利用乘方的相關知識解決生活問題.

二、“點全·線聯·面融”式教材解讀

1.知識點解讀——點全

乘方是有理數的一種基本運算，它是有理數乘法的推廣和延續.讓學生結合自己的生活經驗，探求乘方的運算方法，在此基礎上對冪、底數、指數的概念以及乘方的符號法則的歸納是本課的知識點.乘方是后續學習有理數的混合運算、科學記數法和開方的基礎，起到承前啟后、鋪路架橋的作用.

2.知識線解讀——線聯

顯性知識線：乘方的意義—乘方的概念解讀—乘方的符號原則.學生對“乘方的意義”已有知識儲備，比較容易接受;“乘方的概念解讀”是全新知識，講解時要透、全;“乘方的符號原則”為后續的有理數乘方的運算打下堅實的基礎.

隱性思想方法線：本節課主要是在生活實踐的基礎上通過類比（類比正方形的面積、立方體的體積）理解乘方的意義，通過特殊到一般掌握有理數乘方的運算本質.“分類討論”數學思想方法起著舉足輕重的作用.

3.知識面解讀——面融

顯性知識面：“有理數的乘方”是 “有理數”這一章節的難點，同時又是整個初中階段“數與式”中很重要的基礎.例如在“代數式”“冪的運算”“實數”等章節中，“乘方”無處不在，處處滲透，足見本課時在初中數學中的重要地位.

隱性能力層面：本課時通過創設問題情境，激發學生學習數學的興趣;通過對乘方意義的探索，培養學生觀察、比較、分析、歸納及概括的能力;通過乘方運算的運用，培養學生的邏輯思維能力;通過乘方的故事以及改編，向學生展示數學與生活的緊密聯系.

三、基于教材解讀的教學實踐

1.創設情境，導出課題

在印度有一個古老的傳說，舍罕王打算獎賞國際象棋的發明人——宰相：西薩·班·達依爾.國王問他想要什么，他對國王說：“陛下，請您在這張棋盤的第1個小格里，賞給我1粒麥子，在第2個小格里給2粒，第3個小格里給4粒，以后每一小格的麥子都比前一小格多一倍.請您把棋盤上64格的麥粒都賞給您的仆人吧！”國王覺得這要求太容易滿足了，就命令人們給他這些麥粒.當人們把一袋一袋麥子搬來開始計數時，國王才發現：就算把全印度甚至全世界的麥粒全拿來，也滿足不了宰相的要求. 那么，宰相要求得到的麥粒到底有多少呢？

評析：將抽象的數學知識寓于故事中，拉近了數學與生活的距離.在解決問題的過程中，數據多而且龐大，學生解決問題的熱情逐漸消減，但是強烈的求知欲促使他們尋求問題的答案，此時，教師導入課題，更加激發了學生的求知欲，為新課的展開做了很好的鋪墊，回答了“知識從哪里來？”的問題.

2.整體構架，引出新知

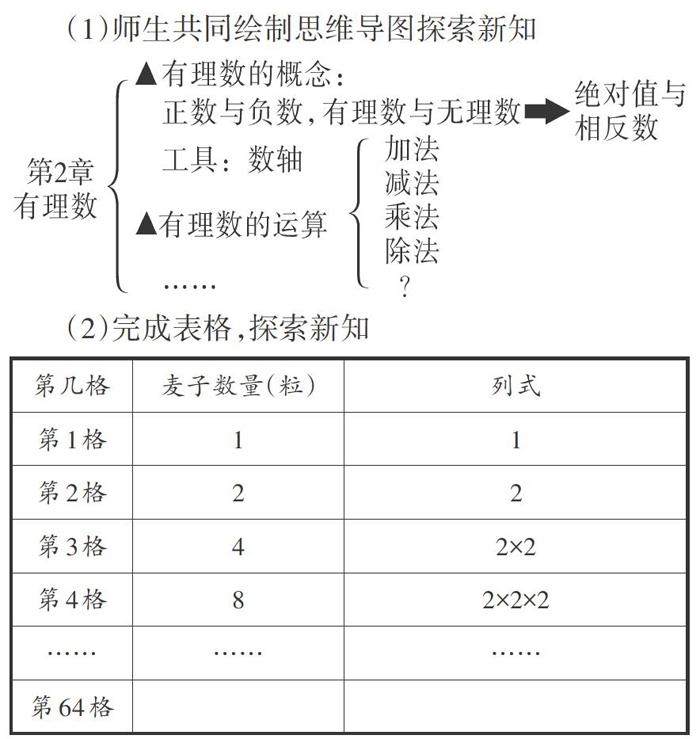
（1）師生共同繪制思維導圖探索新知

（2）完成表格，探索新知

評析：利用思維導圖將所學知識進行回顧，將知識在“面”上打開，連成“線”，在“點”上分析，讓學生發現現有的知識儲備并不能解決問題，從而產生強烈的探知欲，在此基礎上展開新知的學習.在新知教學過程中，讓學生經歷 “知識是怎樣形成的？”的問題預設和解決過程，在這個過程中“類比”乘法的本質理解乘方的本質，再教學乘方的定義及有關概念，引導學生從本質上理解[an≠an]，讓學生用冪來表示表格中的式子，將知識的易錯點和混淆點在本質上厘清.

3.理解本質，運用新知

辨析 （-4）2、-42的區別與聯系，并分別指出它們的底數和指數.

評析：在這個環節中，帶領學生體驗新知應用過程中的矛盾沖突點，并讓學生運用所學的相反數知識以及“整體思想”解決矛盾沖突.這是一個舊知喚醒以及新知應用的過程，學生在無形中將零散的知識點串成線、織成網，進而達到了“面”的統一.本環節回答了“知識學后有什么用？”的問題.

4.尋求變式，提升認識

故事續編：正當國王為拿不出那么多糧食而犯愁的時候，宰相哈哈大笑了起來，說：“尊敬的陛下，能為您發明國際象棋是我的榮幸，剛剛我和您開了個玩笑.要不這樣吧，陛下，請您在這張棋盤的第1個小格里，賞給我1元硬幣，在第2個小格里給第1個小格的一半錢數，第3小格給第2小格的一半錢數，以后每一小格的錢數都是前一小格錢數的一半.請您把棋盤上64格的錢，都賞給您的仆人吧！”這下國王放聰明了，細細算了起來，算完后，他和宰相不約而同地笑了起來.同學們，你知道他們為什么笑了嗎？

嘗試：學了本節課的知識，你能創編一些數學小故事嗎？

評析：故事續編，首尾呼應，引導學以致用，在故事中尋找數學的奧秘.同時，將課堂還原到生活中，這時學生已經不再是用冗長的乘法式子來表示，而是用簡潔的冪來表示.引導學生用所學的數學知識去解決問題，提高學生的應用意識.本環節回答了“知識向哪里去？”的問題.至此，“知識從哪里來？知識是怎樣形成的？知識學后有什么用？知識向哪里去？”串起了一條完整的教學活動主線.

數學課程目標從注重“雙基”到三維目標，再到核心素養目標，將數學教學定位到育人的終極目標上.讓學生將思維過程、方法策略內化為解決問題的基本認識、基本素質、基本態度及基本思想.而這些素養具體在學生身上怎么體現？在課堂教學中如何落實？教師必須說清楚、講明白、做到位，這也是筆者將長期探索的問題.

“預設”的完美不及“生成”的精彩.經驗豐富的教師會多角度、多維度地緊扣學生的學習實際設計教學預設，通過提問、追問、操作、討論等形式完成預設目標.但是課堂的精彩來自于課堂的生成.在課堂的小結部分，有學生闡述了“乘方只是書寫比較簡單，但是運算還是要依靠乘法計算”的理解;有學生提出了疑問：“幾個相同的數的加法可以用乘法表示（2+2+2=3×2），幾個相同數的乘法可以用乘方表示（2×2×2=23），那么幾個相同數的減法（2-2-2）、除法（2÷2÷2）可以怎么表示呢？”還有學生針對本節課的思維導圖，提出了“是否還有第五種有理數的運算方法？”的問題……這些精彩的課堂生成補全了“點”，延長了“線”，拓展了“面”，健全了“體” .

[參考文獻]

羅增儒.核心素養與課堂研修[J].中學數學教學參考，2017（23）：14-20.

（責任編輯 陳 昕）