基于權衡空間探索的多約束彈道初值確定方法

何兆偉，葛 冰，徐利杰，李平岐

(1. 北京宇航系統工程研究所，北京 100076；2. 中國長征火箭有限公司，北京 100070)

0 引言

智慧火箭研制的目標是實現設計和試驗效率的提升，具體表現為：1周完成總體構型優化、1個月完成總體方案設計且一次成功率100%[1]。而在火箭總體設計中，彈道設計起著極其重要的作用，火箭總體方案、設計參數、運載性能與飛行方案都是根據彈道設計的結果而確定的[2]。運載火箭彈道設計是一種典型的非線性規劃問題[3]，設計過程除了要符合火箭自身構型特點和有效載荷入軌要求外，還要滿足發射場、落區、飛行安全、地面跟蹤測量與控制等約束條件。算法對初值的設置較為敏感，常出現運算發散的情況[4]，特別是在發射任務類型變化時，現有工程設計方法還較為依賴人員的自身經驗，需要進行部分手動調整和優化。

本文從解決上述問題出發，對不同初值給定方法[5-8]進行了大量仿真研究。最終通過引入多屬性權衡空間探索及全局優化思想，結合彈道設計需求建立了權衡空間中方案的評價指標，給出了初值搜索方法并據此重塑了工程彈道設計流程。同時，以較為復雜的三級半且末級兩次啟動的液體運載火箭為對象進行了仿真驗證。

1 彈道設計模型

1.1 彈道計算

彈道計算采用旋轉橢球地球模型，考慮攝動項影響，所用動力學模型和飛行程序設計方法參見文獻[9]。

工程彈道計算中使用“彈道級”的概念以提升設計配置的通用性和適用范圍，每一個飛行段即為一個彈道級，包括結構級(含質量特性、加注諸元、動力參數等)、導引、關機、控制、氣動、飛行程序、分離和通用屬性等對象。每個彈道級按圖1所示流程進行計算并積分，全部彈道級積分完成即完成了一條彈道的計算。

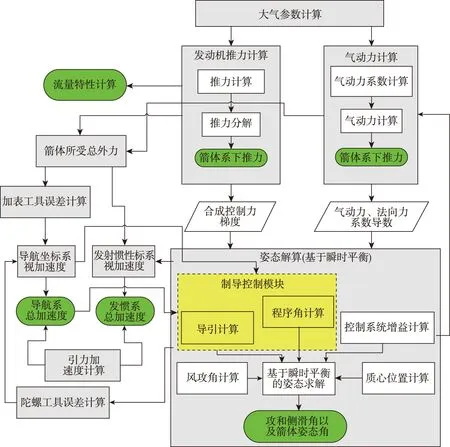
圖1 彈道級計算流程Fig.1 Calculation process of trajectory stage

1.2 迭代設計

彈道迭代設計的思路為通過對控制矢量X=[x1,x2,…,xn]的攝動來計算對入軌參數，即目標矢量Y=[y1,y2,…,yn]的影響，通過Y與入軌要求的偏差解算X的增量，直至偏差符合精度要求[3,10]。針對半長軸、近地點高度、遠地點高度、入軌點矢徑等長度目標變量，通常精度要求取1×10-1m；針對軌道傾角、近地點幅角、升交點經度、彈道傾角、分離時刻攻角等角度目標變量，通常精度要求取1×10-4°。

數學模型為構建雅克比矩陣

(1)

通過高斯消元法求解X的增量

(2)

設計流程如圖2所示。

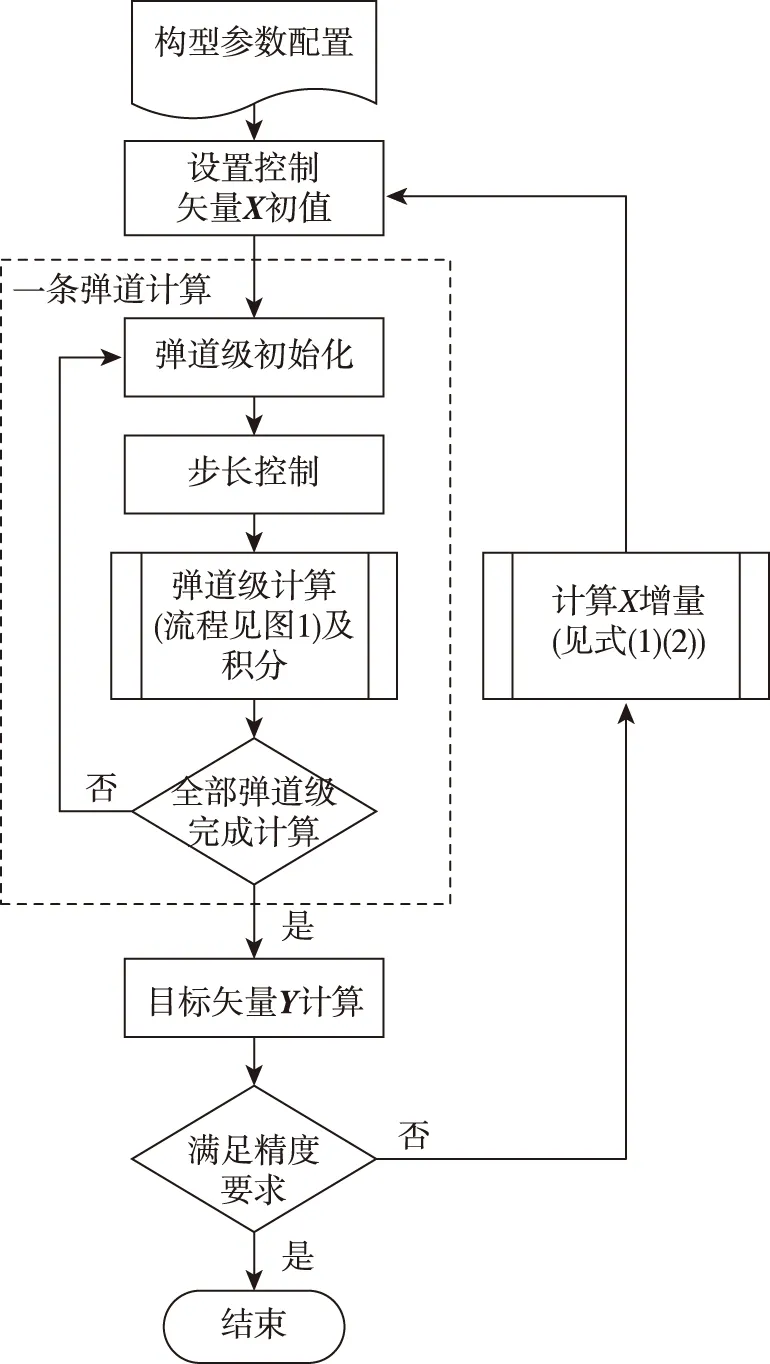
圖2 彈道迭代設計流程Fig.2 Design process of trajectory

針對低軌圓軌道，Y的各分量一般選取半長軸a、入軌點地心矢徑r、入軌點速度v、入軌點彈道傾角θ等；針對高軌地球同步轉移軌道，Y的各分量一般選取近地點高度hp、遠地點高度ha、近地點幅角ω、軌道傾角i等。而X的各分量一般在考慮火箭構型特點、設計約束及對Y敏感度的基礎上，選取射向A0、不同彈道級的俯仰程序角φi、偏航程序角ψi、關機時間ti等參數。

X和Y的選取和對應關系，以及其對設計收斂性的影響，也體現出了任務類型變化對火箭彈道設計過程的影響，以及人為經驗在設計過程中起到的作用。

2 初值確定方法

2.1 問題描述

如圖2所示，彈道設計流程最初要選定控制矢量X的分量并給定初值，參數選擇適當則算法收斂，得到滿足入軌精度要求的彈道設計結果。該算法及流程的優點在于可快速得到精確解，缺點在于對初值敏感，若初值距真值較遠、不在收斂域內，則計算發散。因此，面向試樣或應用飛行階段的運載火箭轉換常規任務類型、承接特殊軌道任務等工程實際場景，或開展新型運載火箭構型論證時，往往無法通過直接將目標矢量Y更改至有效載荷入軌要求的方式自動得到設計結果，而需要人為手動調整，結合設計人員的經驗對初值進行探索直至其進入收斂域內。方法的自動化、智能化程度低，設計效率有待提升。

2.2 方法與流程

結合權衡空間探索與全局優化的思想確定彈道設計的初值。

根據多屬性權衡空間探索方法[11]，控制矢量X的不同取值可達到不同的效用和成本。這就構成了一個權衡空間，代表了決策者所有的設計選擇，空間中每個點都是一個備選方案，探索權衡空間就是對備選方案進行權衡評估尋找最優解[12]。為兼顧局部收斂及全局搜索能力，采用改進粒子群算法(PSO算法)[13]對權衡空間進行全域搜索。即將每個控制矢量Xi(i=1,2,…,m)抽象為沒有質量和體積的微粒，并延伸到n維空間，粒子Xi在n維空間里的位置表示為一個矢量[xi,1,xi,2,…,xi,n]，每個粒子還有一個速度矢量[vi,1,vi,2,…,vi,n]決定了它們的搜索方向和距離。所有粒子都有一個由被優化函數決定的評價指標值f，粒子知道自身到目前為止發現的最好位置(pbest)和現在的位置，即自身經驗；也知道整體粒子群體發現的最好位置(gbest)，即同伴經驗。粒子通過自身經驗和同伴經驗來決定下一步的搜索運動，以達到全局探索和局部開采的平衡。

取評價指標

(3)

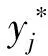
權衡空間搜索的步驟如下：

1)隨機生成權衡空間中m個控制矢量Xi的位置和速度；

2)將當前每個Xi的位置和評價值fi存在Xi的pbest中，將所有pbest中fi最小的Xi的位置和評價值存在gbest中；

3)用式(4)更新每個Xi的速度和位置；

vi,j(t+1)=wvi,j(t)+c1r1[pi,j-xi,j(t)]+
c2r2[pg,j-xi,j(t)]
xi,j(t+1)=xi,j(t)+vi,j(t+1),j=1,2,…,n

(4)

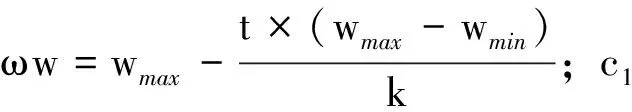
4)將每個Xi的評價值fi與其經歷過的最小值比較，若較小則更新其pbest，比較當前所有pbest和gbest，若較小則更新gbest；

5)若滿足停止條件(迭代輪次達到k，或gbest中的f值小于等于預設的截至條件f*)，則輸出結果，否則返回3)步。

將初值確定方法嵌入設計流程，重塑的工程彈道設計流程見圖3。可以看出，初值確定方法與現行成熟的工程設計算法有機銜接(利用現有流程中的彈道計算進行評價值計算，得到收斂域內的初值后交還給迭代設計)，程序復雜度低，使得該方法完全符合工程實際應用需要。

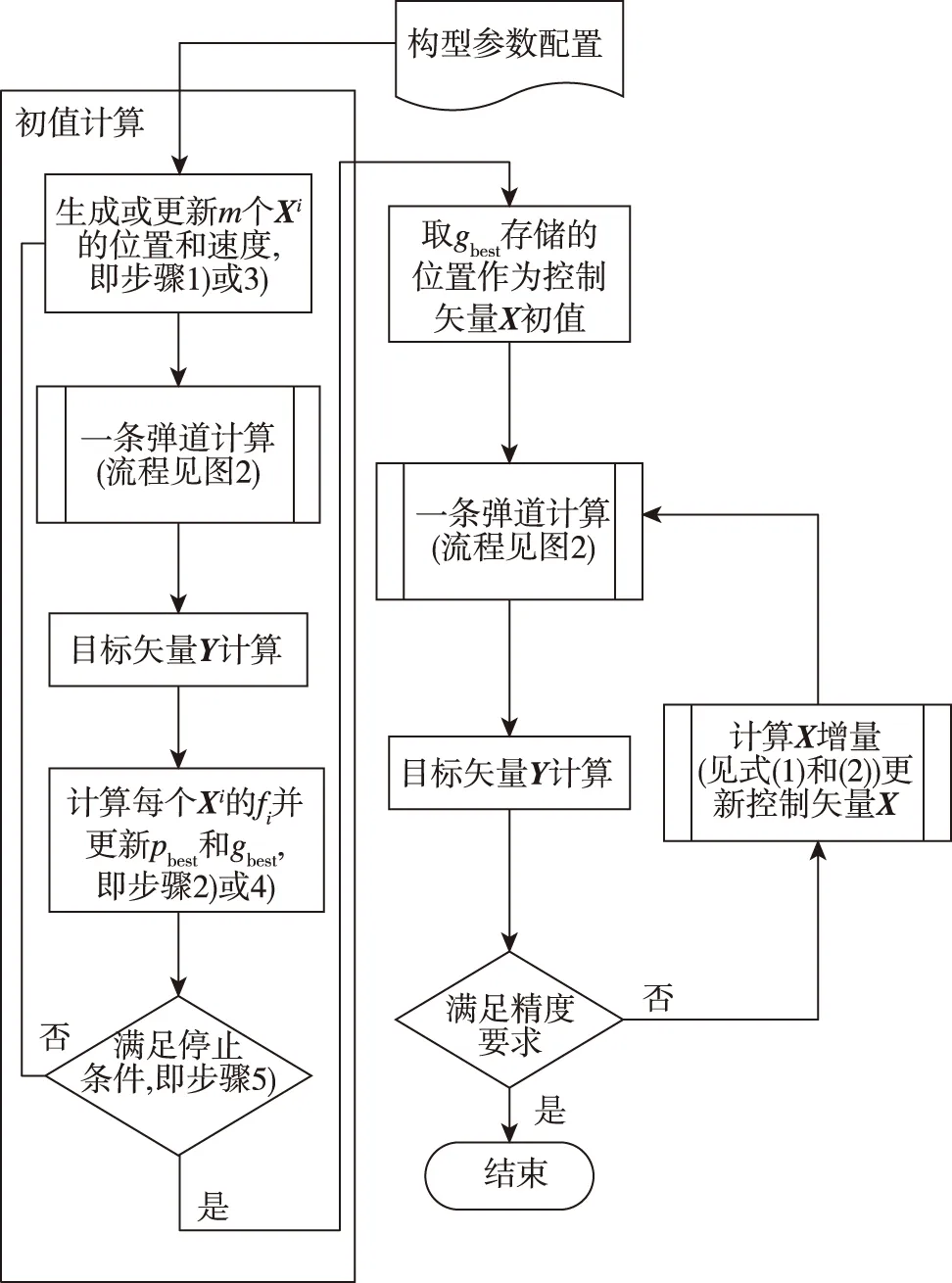
圖3 增加初值計算后的彈道設計流程Fig.3 Design process of trajectory with initial values calculation

3 仿真計算效果

3.1 仿真條件

以較為復雜的三級半、末級兩次啟動、常規發射任務為高軌GTO載荷的液體運載火箭為對象，完成新低軌任務彈道設計，在滿足各項約束的同時，終端入軌條件如表1所示。

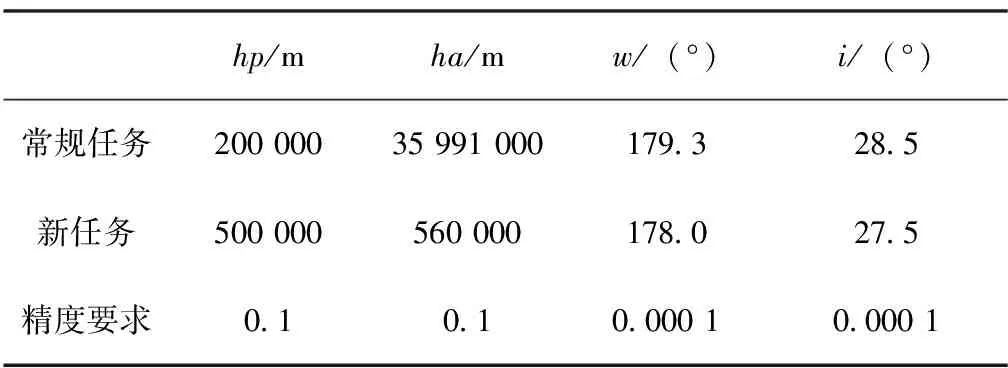
表1 終端條件

采用分解策略[4]對三級半運載火箭進行彈道設計，求解策略及控制矢量、目標矢量的選取見表2。

表2 求解策略

3.2 仿真結果分析

火箭常規GTO任務控制矢量X的設計結果為[-15.124 1°, - 85.452 0°, 2.434 6°, 177.044 0 s]，以此作為初值，應用工程現行設計流程(圖2)的收斂性如圖4所示。可以看出，目標變量在迭代約10輪以后開始發散。

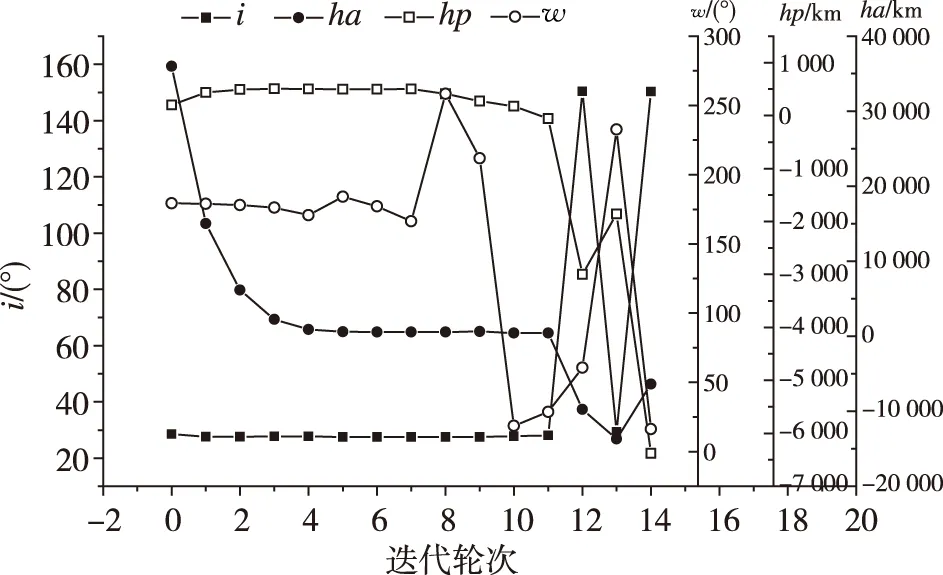
圖4 工程現行設計流程的收斂性曲線Fig.4 Convergence curve using original design process

應用2.2節權衡空間搜索方法進行初值計算，取粒子數m=30，迭代輪次k=500，評價值截止條件f*≤1×10- 8，權重調節系數ξj均取1，慣性權重w的計算中wmax=0.9和wmin=0.4，學習因子c1和c2均取1.5。

經仿真計算，得到評價值f的變化曲線如圖5所示。最小值fmin=1×10- 6，對應gbest中控制矢量X的位置為[19.697 1°, -97.719 3°, 25.983 0°, 44.996 7 s]，以此為初值進行彈道迭代設計的收斂性如圖6所示。由圖6可以看出，迭代約30輪左右收斂，目標矢量Y最終收斂至[500.000 0 km, 178.000 0°, 27.500 0°, 560.000 0 km]，滿足終端條件精度要求，X的最終設計結果(真初值)為[19.675 4°, -97.814 3°, 25.719 4°, 44.894 1 s]。由圖7可以看出，X逐步接近真初值的收斂過程。

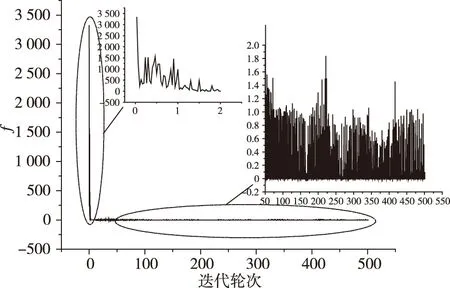
圖5 評價值f曲線Fig.5 Curve of evaluation value

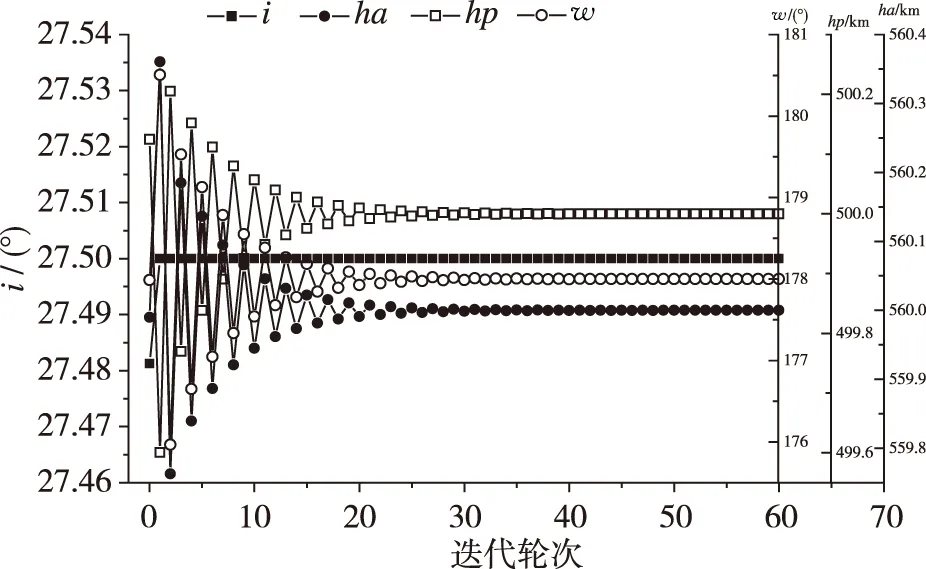
圖6 新流程下的目標矢量收斂性曲線Fig.6 Convergence curve of target vector using new design process

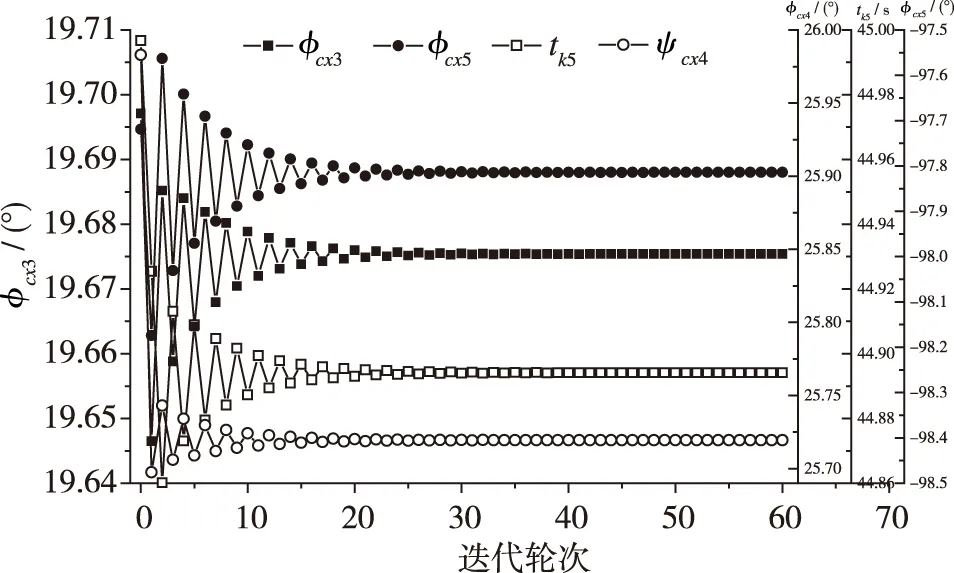
圖7 新流程下的控制矢量收斂性曲線Fig.7 Convergence curve of control vector using new design process

4 結論

本文著重解決多約束運載火箭彈道設計的初值敏感問題。在梳理了當前工程彈道計算及迭代設計詳細流程的基礎上，將多屬性權衡空間探索和全局優化思想有機結合，提出了彈道設計初值確定方法，并重塑了彈道設計流程。仿真結果表明：

1)按新流程設計的彈道滿足全部過程約束條件及最終入軌精度要求。

2)針對不同終端約束條件，可在不改變控制和目標變量選取，且不改變設計初值的情況下，自動收斂得到設計結果。

3)方法解決了初值敏感性問題，具有快速、全局的特點，并與現行成熟的工程設計算法有機銜接，復雜度低，符合工程實際應用需要。

應注意的是，在火箭應用發射常規任務彈道設計時，依然是傳統設計方法計算效率更高，本文給出的方法及流程主要面向新構型、新任務類型下的設計工作。同時，方法針對如評價值f的截至條件等參數的取值，目前尚未形成統一的標準，要結合具體的任務問題來設置，因此，還需繼續深入探索，不斷提高方法的計算效率。