航天飛行器典型高溫透波結構熱匹配性能分析

張瑾瑜，雷 豹，楊東生，許俊偉，嚴 旭

(中國運載火箭技術研究院，北京 100076)

0 引言

航天飛行器高溫透波結構是在惡劣使用環境條件下保護航天飛行器的通信、遙測、制導、引爆等系統天線正常工作的一種結構，如天線罩、天線窗等，其材料常選用石英玻璃、石英陶瓷、石英纖維增強二氧化硅、氮化硅、磷酸鹽復合材料等耐高溫多功能電介質材料[1-6]。隨著航天飛行器的不斷發展，飛行速度不斷提高，面臨的熱環境也越來越惡劣，而高溫透波結構與其安裝結構的材料熱膨脹系數存在一定差異，在惡劣熱環境條件下，它們之間可能產生較大的熱變形，進而可能導致高溫透波結構在熱應力作用下破壞失效。因此，研究高溫透波結構的熱匹配性能，對航天飛行器的發展具有重要意義[7]。

本文針對一種航天飛行器典型天線窗類高溫透波結構及其安裝形式，選取典型熱環境條件，采用有限元仿真分析方法，研究高溫透波結構在不同材料、不同尺寸條件下的熱匹配性能。

1 結構及連接形式

航天飛行器典型天線窗及其安裝結構如圖1所示，天線窗通過鋁合金底座和鋁合金壓環固定連接后，貼壁安裝在航天飛行器金屬殼體內壁面上。

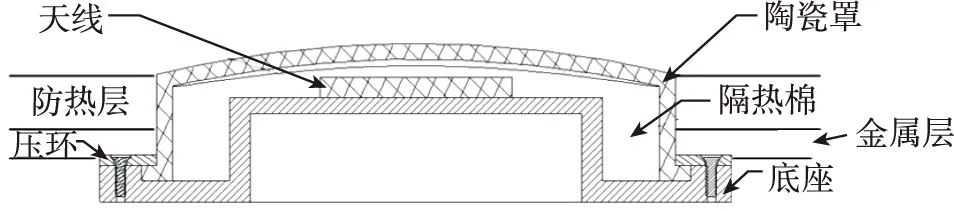
圖1 天線窗及其安裝結構示意圖Fig.1 Schematic diagram of antenna window and its installation structure

表1為天線窗結構選用石英玻璃、石英陶瓷、石英纖維增強二氧化硅、氮化硅等不同材料的主要性能參數[8-11]。

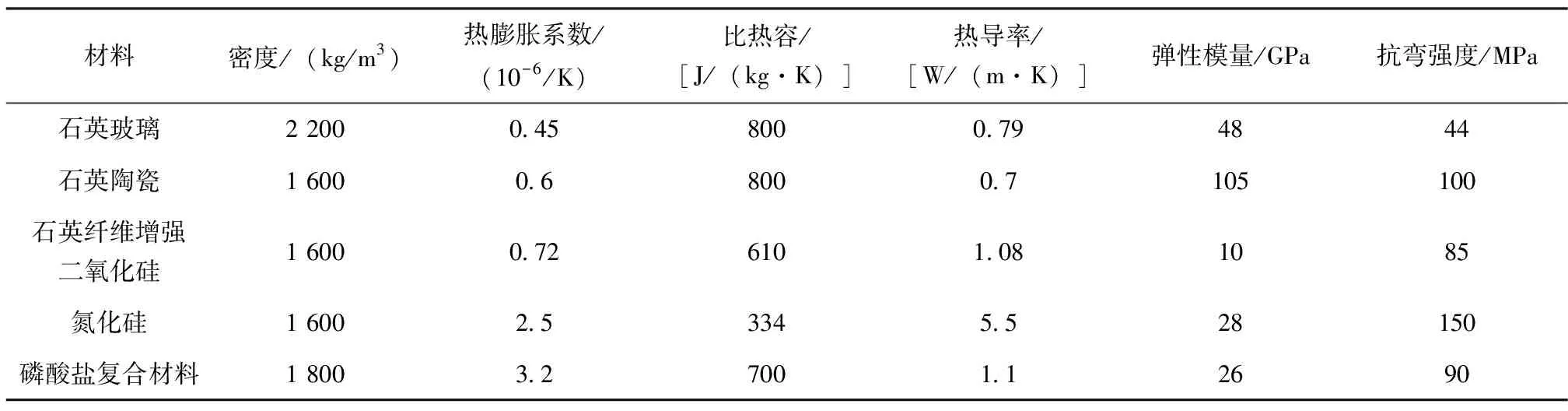
表1 材料性能參數

2 熱應力數學模型

結構受熱產生的熱變形、熱應力等熱匹配性能主要與材料熱膨脹系數、彈性模量及溫度變化量有關[12]。

熱變形量的計算公式為

ΔL=λLΔt

(1)

式中, ΔL代表結構受熱產生的變形量，λ代表熱膨脹系數，L代表結構線性尺寸，Δt代表溫度變化量。

假設兩種材料的溫升相同，則熱應力計算公式為

σ=EcΔt(λc-λs)

(2)

式中,σ代表結構受熱產生的熱應力，Ec代表材料彈性模量，Δt代表溫度變化量，λc和λs代表熱匹配結構的材料熱膨脹系數。

本文主要針對高溫透波天線窗結構的材料性能、結構尺寸研究其熱匹配性能。

3 有限元分析

3.1 有限元模型建立

1)模型假設。假設天線窗與其安裝結構之間無間隙。取非金屬材料表面黑度0.8，金屬材料表面黑度0.3。根據項目要求，初溫設置為60℃。考慮熱輻射，波爾茲曼常數5.67×10-8W/(m2·K4)。針對金屬殼體等塑性材料，不考慮對結果影響較小的倒角、圓角等結構特征。

2)幾何建模。用CATIA軟件建立天線窗及其安裝結構的幾何模型并導入Abaqus，如圖2所示。

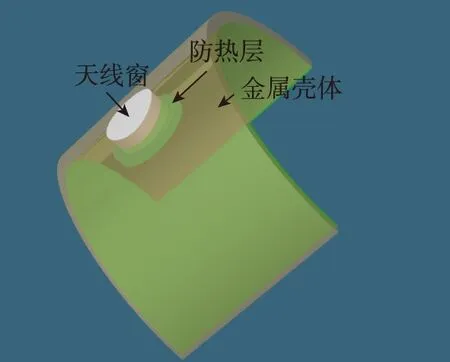
圖2 天線窗及其安裝結構的三維模型Fig.2 3D model of antenna window and its installation structure

3)網格劃分。采用力熱耦合四面體單元C3D8T和Abaqus內置的力熱耦合分析方法進行分析計算，如圖3所示，共生成94 663個節點和67 082個單元。

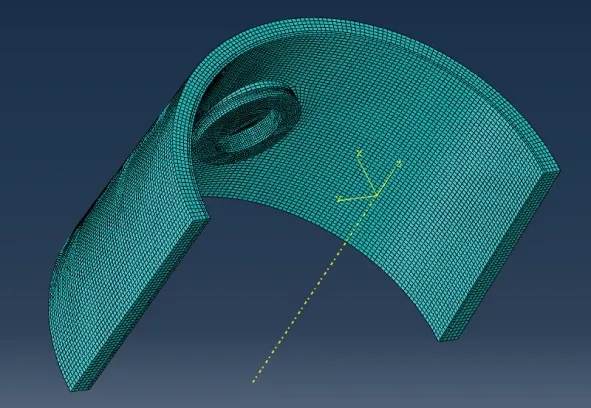
圖3 天線窗及其安裝結構的有限元網格Fig.3 Finite element mesh of antenna window and its installation structure

4)材料性能參數。天線窗結構貼壁安裝在航天飛行器金屬殼體內壁面上并與防熱層接觸，金屬殼體材料為ZL114A，防熱層為低密度石英酚醛，天線窗材料性能參數見表2。

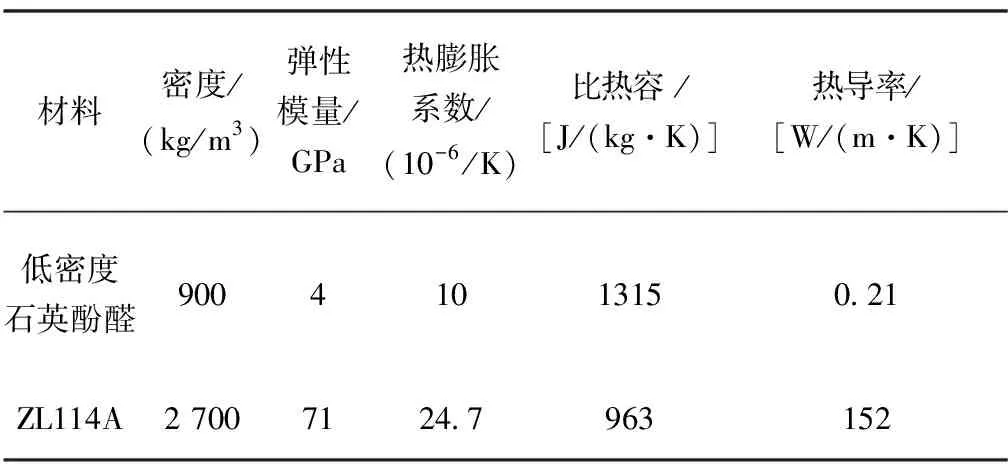
表2 材料性能參數

5)載荷數據。選用典型航天行器熱環境條件進行天線窗結構熱匹配分析，如圖4所示。冷壁熱流最高300 kW/m2，冷壁熱流總加熱量30 000 kJ/m2，恢復焓最高1 800 kJ/ m2。

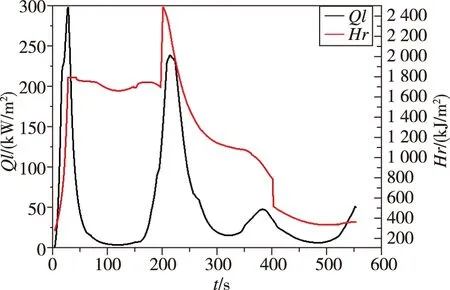
圖4 典型天線窗熱環境條件Fig.4 Typical thermal load curves of antenna window

6)接觸定義及設置。本文采用的有限元模型為軸對稱模型，如圖5所示，防熱層與金屬殼體、金屬殼體與壓環、壓環與底座之間均定義綁定約束，其余定義接觸，并設置對稱邊界，底端固支。

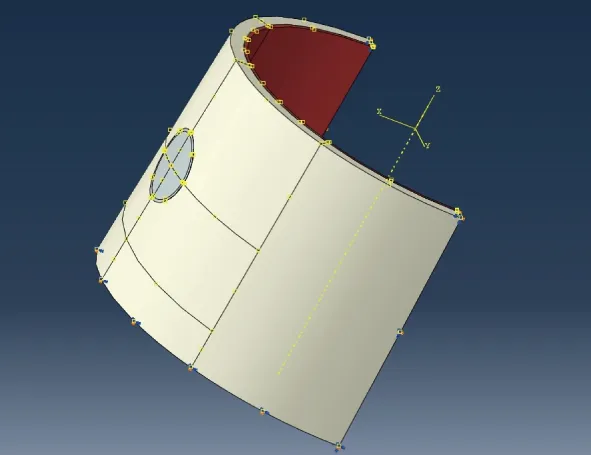
圖5 有限元模型示意圖Fig.5 Finite element analytical model

7)防熱計算。初溫設置為60℃，材料表面輻射系數0.8。提交計算后，獲得天線窗及其安裝結構的溫度場分布。

8)熱應力計算。將天線窗及其安裝結構的溫度場分布導入計算模型，作為熱應力計算的輸入。在材料性能參數中設置強度數據，提交計算后，獲得天線窗及其安裝結構的熱應力分布。

3.2 結果分析

以石英纖維增強二氧化硅天線窗為例，對有限元計算結果進行分析，計算結果表明：天線窗熱變形及熱應力變化規律一致，均在末秒達到最大值，最大變形量為0.3 mm，最大拉應力為17.9 MPa，最大壓應力為15.2 MPa，位于天線窗側壁，如圖6和圖7所示。

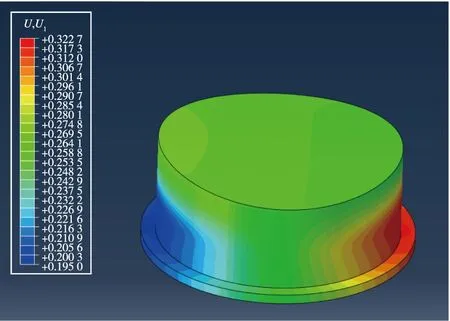
圖6 天線窗位移分布圖Fig.6 Displacement distribution of antenna window

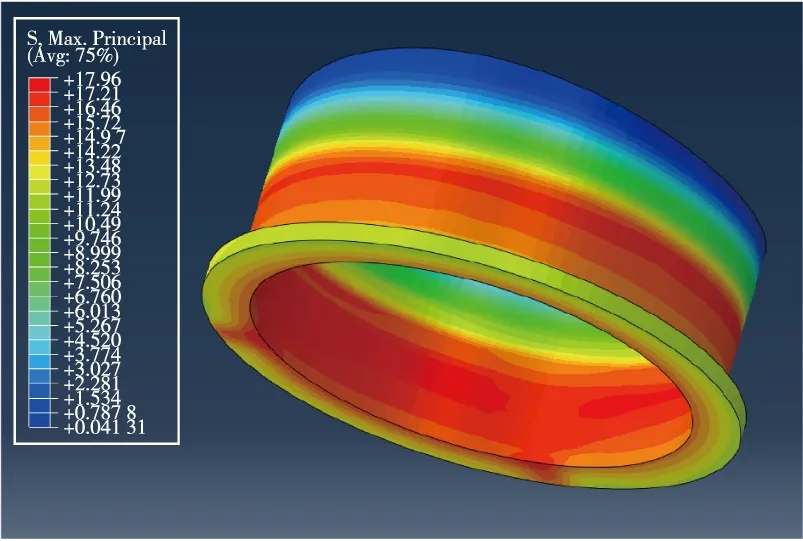
(a)天線窗最大拉應力分布圖

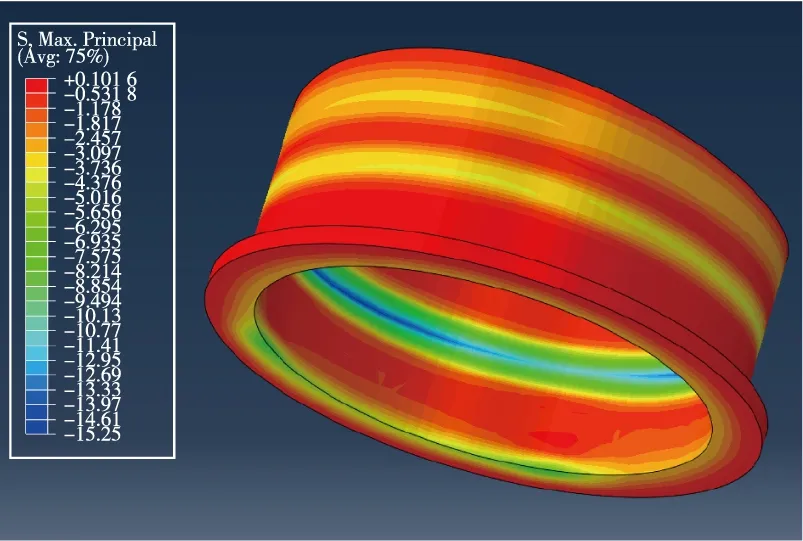
(b)天線窗最大壓應力分布圖圖7 天線窗應力分布圖Fig.7 Stress distribution of antenna window

對天線窗、防熱層及金屬殼體溫度隨時間變化的關系曲線進行分析，如圖8所示。從圖中可以看出：防熱層與天線窗溫度隨時間變化規律基本一致，且溫度差值小；金屬殼體與天線窗溫度隨時間變化規律差別大，且溫度差值大；金屬殼體末秒溫度達最高，此時天線窗熱變形、熱應力也達到最大值。

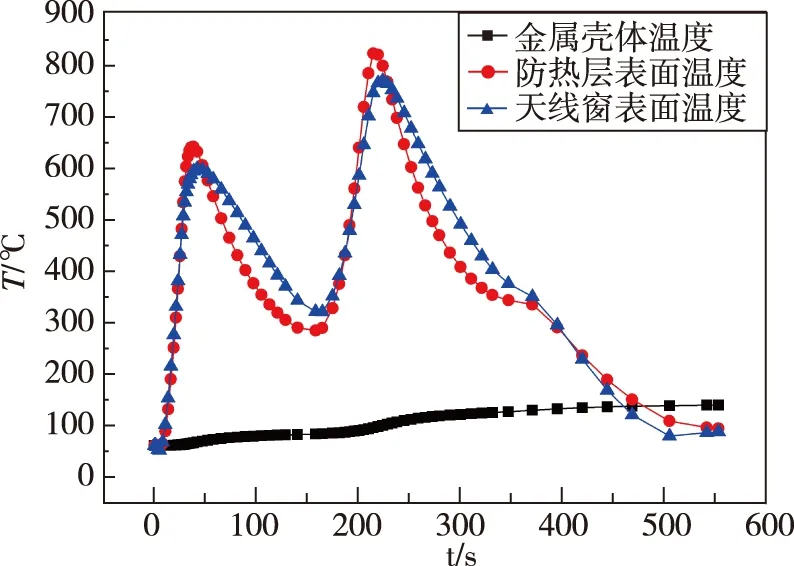
圖8 溫度隨時間變化曲線圖Fig.8 Temperature curves with time

分析認為，天線窗熱匹配產生的熱變形、熱應力主要與金屬殼體受熱膨脹有關。金屬殼體在末秒溫度達到最高，由式(1)可知，此時金屬殼體熱膨脹量也達最大值，因此,天線窗熱匹配產生的熱變形、熱應力在末秒達到最大值。

3.3 材料性能對熱匹配的影響

由上文分析可知，天線窗結構熱匹配產生的熱變形與熱應力的變化規律一致，下文主要通過熱應力分析材料性能對熱匹配的影響。在相同熱環境條件下，保持天線窗結構尺寸參數不變，對比分析了選用不同高溫透波材料時結構熱匹配產生的熱應力，仿真計算結果得到熱應力排序為：石英陶瓷>石英玻璃>氮化硅>磷酸鹽復合材料>石英纖維增強二氧化硅,如表3所示。

表3 不同材料天線窗熱應力計算結果

分析認為,材料彈性模量是影響天線窗熱匹配性能的主要因素。不同材料天線窗結構熱匹配產生的熱應力與材料彈性模量變化規律一致，如圖9所示。由于5種材料的熱膨脹系數相近，均遠小于金屬殼體熱膨脹系數，且熱物理性能參數相差不大，溫升變化量相當，如圖10所示。由式(2)可知，材料彈性模量成為影響結構熱應力的主要因素，仿真分析計算結果與理論分析一致。

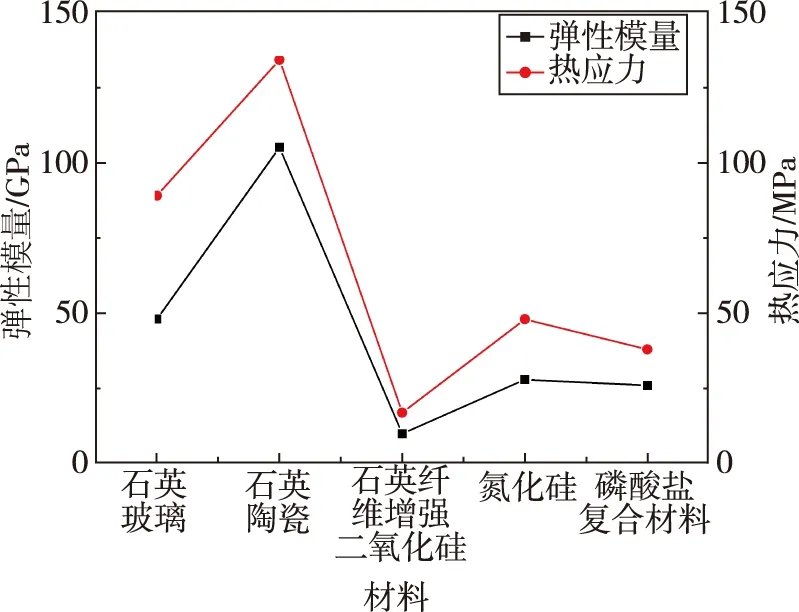
圖9 不同材料熱應力及彈性模量變化曲線圖Fig.9 Thermal stress and modulus of elasticity ofdifferent materials

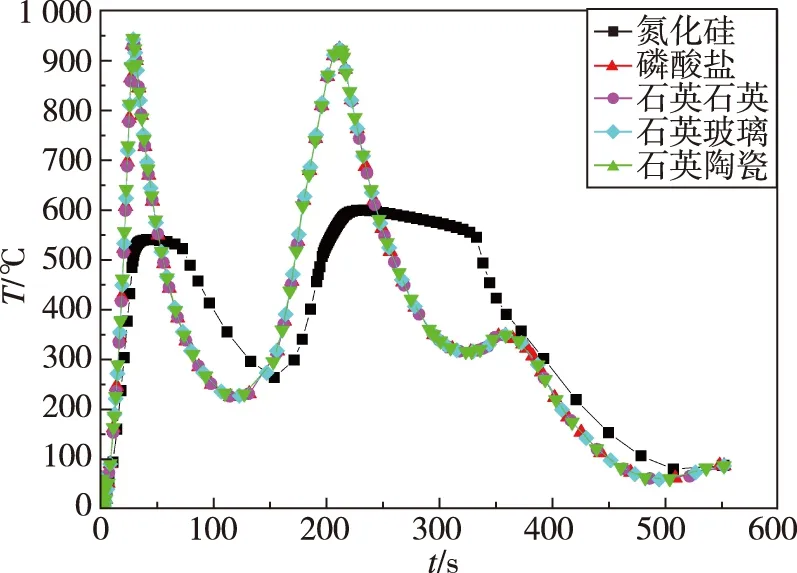
圖10 不同材料天線窗表面溫度隨時間變化關系曲線圖Fig.10 Temperature curves of antenna window’s surface with time for different materials

結合材料抗彎強度，進行不同材料天線窗剩余強度系數分析，剩余強度系數計算公式如下

η=σb/σ

(3)

式中，η代表剩余強度系數，σb代表材料強度極限，σ代表結構產生的最大應力。已知天線窗熱匹配最大熱應力為拉應力，陶瓷材料的抗拉強度為抗彎強度的80%～97%[13]，剩余強度系數計算結果如表4所示。由表4可知，石英纖維增強二氧化硅天線窗結構熱匹配產生的熱應力剩余強度系數大，材料具有優越的熱匹配性能。

表4 不同材料天線窗剩余強度系數

3.4 結構尺寸對熱匹配的影響

在相同熱環境、相同材料條件下，對比分析不同材料尺寸條件下天線窗結構熱匹配產生的熱應力，天線窗尺寸組合如表5所示。

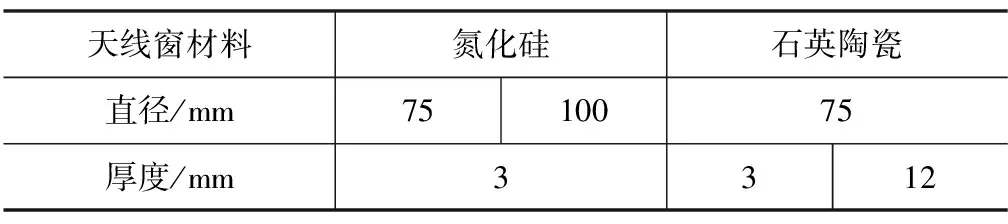
表5 天線窗尺寸組合

仿真計算結果如表6和表7所示。厚度3 mm氮化硅天線窗，直徑75 mm時最大拉應力為48 MPa，直徑100 mm時最大拉應力為132 MPa；直徑75 mm石英陶瓷天線窗，厚度3 mm時最大拉應力為134 MPa，厚度12 mm時最大拉應力為68 MPa。

表6 不同直徑天線窗熱應力計算結果(3 mm氮化硅)

表7 不同厚度天線窗熱應力計算結果(φ75 mm石英陶瓷)

對計算結果進行分析后認為，天線窗直徑越小、厚度越大，熱應力越小，結構熱匹配性能越好，對實際工程應用具有借鑒意義。

4 結論

本文針對一種航天飛行器典型天線窗類高溫透波結構及其安裝形式，通過有限元仿真分析方法，分析了其熱匹配性能及在不同材料、不同尺寸條件下的熱匹配性能，為其在航天飛行器上的應用提供了參考，具體結論如下：

1)天線窗結構熱匹配產生的熱變形、熱應力主要與航天飛行器金屬殼體受熱膨脹有關，與防熱層關系較小，當金屬殼體溫度最高時天線窗結構熱應力達最大值；

2)在相同熱環境條件下，不同材料的天線窗熱應力排序為：石英陶瓷>石英玻璃>氮化硅>磷酸鹽>石英纖維增強二氧化硅，與材料的彈性模量變化規律一致，結合材料抗彎強度，分析認為石英纖維增強二氧化硅天線窗具有更優越的熱匹配性能；

3)天線窗直徑越小，厚度尺寸越大，熱應力越小，結構熱匹配性能越好，對實際工程應用具有借鑒意義。