采用奇異能量譜與改進ELM的軸承故障診斷方法

葛興來， 張鑫,2

(1.西南交通大學 磁浮技術與磁浮列車教育部重點實驗室，成都 611756；2.西南交通大學 唐山研究生院，河北 唐山 063000)

0 引 言

異步電機因其調速范圍寬、效率高、結構簡單等優點廣泛應用于高速列車牽引傳動系統中[1-3]。異步電機軸承作為轉子系統中最重要的組成部分，其運行環境極為復雜，并長期處于高速、高載、高溫狀態下，故障發生頻率較高。相關數據表明，軸承類故障占電機總故障類型的40%～50%[4-6]，是異步電機最常發生的故障類型，嚴重威脅著高速列車的安全穩定運行。因此，實現軸承故障的有效診斷已成為學者們的研究熱點。

文獻[7]采用Hilbert變換構造定子電流解析信號并提取其平方包絡線，利用平方包絡線中的故障特征頻率進行電機軸承的故障診斷，但在空載條件下，異步電機的定子電流較小，故障特征較為微弱，不利于軸承故障的特征提取。因此，不受負載條件影響的振動信號廣泛應用于電機軸承故障之中。文獻[8]將小波包分解法、經驗模態分解法與雙譜分析法相結合實現了軸承故障特征頻率的提取；文獻[9]采用奇異值分解技術解決了經驗模態分解存在的模態混疊問題，實現了軸承內圈、外圈的故障診斷，但是存在奇異值分解中Hankel矩陣行列數選取困難的問題；文獻[10]利用變分模態分解提取軸承振動信號的故障特征，并采用標準模糊C均值聚類法進行故障辨識，但存在變分模態分解參數影響特征提取效果的問題；文獻[11]提出一種基于集合經驗模態分解-Hilbert包絡譜與深度信念網絡的滾動軸承狀態識別方法，但是該方法存在滾珠體故障狀態辨識精度低的問題；文獻[12]提出了基于時域、頻域、時頻域的多域特征提取方法，實現了軸承不同類故障與故障程度的有效評估，但是該方法對于訓練數據與測試數據存在分布差異時，會出現模型泛化能力差的問題。

極限學習機(extreme learning algorithm, ELM)具有結構簡單、訓練速度快、泛化能力強的優點，在模式識別中有著廣泛的應用[13]。但是傳統的ELM由于輸入權值與隱含層閾值的隨機性，會對其訓練效果與診斷效果產生一定的影響。針對上述存在的問題，本文將差分演化算法與ELM相融合，采用自適應差分演化極限學習機(self-adaptive different evolution extreme learning algorithm,SADE-ELM)進行故障辨識，進而研究了一種異步電機軸承故障診斷的新方法。針對于變分模態分解(variational mode decomposition,VMD)存在分解層數與懲罰因子選擇困難的問題，本文采用粒子群算法，通過迭代尋優確定最優參數組合，并利用最優參數組合對軸承振動信號進行VMD分解得到若干本征模態函數(intrinsic mode function,IMF)，并計算不同故障類型的奇異能量譜；根據不同故障下奇異能量譜的差異建立故障特征向量；并通過SADE-ELM進行故障辨識，以提升傳統ELM模型的泛化能力。并通過對不同負載條件下的內圈、外圈、滾珠故障進行診斷，驗證了所提出方法的可行性。

1 基于改進VMD的特征提取方法

1.1 VMD原理

VMD分解是一種新興的信號處理方法[14]，分解的關鍵在于對變分模型的構造與求解。相應的變分模型為：

(1)

式中：f為輸入信號；t為時間；δ為狄拉克分布；{uk}={u1,u2,…,uk}代表分解得到的k個IMF分量；{ωk}={ω1,ω2,…,ωk}為各IMF的頻率中心。

求解變分模型最優解時需構建增廣Lagrange函數，其表達式為：

L({uk},{ωk},λ)=

(2)

式中：α為二次懲罰因子；λ為拉格朗日因子。

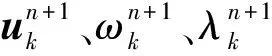
(3)

將式(3)變換至頻域求解，并寫成非負頻率積分的形式，經過二次優化，最終可得各模態分量的表達式為

(4)

同理，中心頻率更新的表達式為

(5)

而λ更新的表達式為

(6)

式中τ表示對噪聲的容許參數。

重復式(4)～式(6)，當滿足迭代條件時可以停止更新，得到若干個IMF分量，否則，繼續進行迭代。迭代停止條件為

(7)

1.2 基于改進VMD的特征提取

VMD算法在進行信號分解時，需要人為選擇分解層數K與懲罰因子α，而K與α的選擇對分解效果有著極為重要的影響。由于電機振動信號較為復雜，K與α兩個參數的選擇通常十分困難，因而合適的參數組合是準確提取軸承故障特征的關鍵。本文采用粒子群優化算法對K與α兩個參數進行以優化，以確定最優的參數組合。

在采用粒子群算法對VMD算法進行優化時，需要先確定適應度函數，通過對比粒子適應度值進行迭代更新。Shannon熵作為一種評價信號稀疏特性的標準，其大小反映了概率分布的均勻性[15]。本文將局部極小熵值作為適應度值，則粒子群算法優化VMD的步驟為：

1)初始化粒子群算法的各項參數并確定尋優過程中的適應度函數；

2)初始化粒子群，以待優化參數組合[K,α]作為粒子群的位置；并隨機產生粒子的初始位置與移動速度；

3)在不同的粒子位置下對信號進行VMD分解，計算每個粒子位置相應的適應度值；

4)對比適應度值的大小并更新個體局部極值與種群全局極值；

5)更新粒子的速度與位置；

6)循環迭代，轉至步驟(3)，直至迭代次數達到最大設定值后輸出最佳適應度值及粒子位置。

軸承信號經過改進VMD分解，可以得到若干IMF分量，可將其組成初始的特征矩陣B，即

B=[IMF1,IMF2,…,IMFk]T。

(8)

式中k為分解得到的IMF個數。

當異步電機發生軸承故障時，各IMF能量發生變化，可以作為區分各類故障的依據。而信號的能量可表示為信號奇異值的平方和，兩者關系如下：

(9)

由式(9)可知，要想表達信號的能量，需要先求出信號的奇異值。因此，需要對特征矩陣B進行奇異值分解(singular value decomposition,SVD)，得到的奇異值矩陣為

S=[s1,s2,…,sk]T。

(10)

為了增強特征向量的魯棒性，需要對其進行歸一化處理，以奇異值能量譜構建故障特征向量，則奇異值能量譜為

(11)

根據奇異能量譜在不同故障間的差異即可實現軸承故障的特征提取。

2 基于改進ELM的故障辨識

為了進一步優化ELM模型，提升其故障辨識能力，本文將差分進化算法與極限學習機相融合，采用SADE-ELM分類器進行故障辨識，以實現電機軸承準確故障診斷。

2.1 ELM原理

ELM是針對單隱含層前饋神經網絡的改進算法，由輸入層、隱含層和輸出層組成。對于N個不同的訓練樣本(xi,ti)其中xi是輸入向量，ti是目標向量，則ELM的輸出函數為

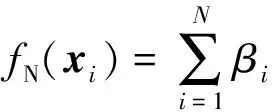
i=1,2,…,N。

(12)

式中：?為激活函數；ωi為輸入層與隱含層間的連接權值；βi為隱含層與輸出層間的連接權值；bi為第i個隱含層神經元的閾值；ωi×xi代表著ωi與xi的內積。式(12)簡化可得

Hβ=T。

(13)

式中H為隱含層的輸出矩陣。則ELM的學習過程為：

1)確定隱含層神經元個數，隨機確定輸入層與隱含層間的連接權值ωi與隱含層神經元的閾值bi。

2)確定激活函數，確定隱含層的輸出矩陣H。

3)計算輸出層權值β=H+T。其中H+為H的Moore-Penrose廣義逆矩陣。

2.2 SADE-ELM分類器

傳統ELM的輸入權值與隱含層閾值的隨機性選擇，會對其訓練效果與診斷精度產生一定的影響。差分進化算法在尋優方面是一種高效、快速的算法，在解決優化問題時，收斂速度較快。然而在差分演化算法中，種群大小、放縮因子、雜交概率三個參數對算法的收斂性和收斂速度有著重要的影響[16]，而如何選擇合理的參數值十分困難。本文采用SADE-ELM分類器實現對差分進化算法參數的自適應選擇，以提升分類器的分類效果。其訓練步驟為：

1)初始化ELM的隱含層神經元個數l以及激活函數?，確定種群的維數D與迭代次數g。第一代種群θ為

(14)

式中：G代表進化代數；k=1,2,…,D。

2)根據種群對網絡的輸出層權重與均方根誤差進行計算，其計算公式為

(15)

(16)

式中m代表分類個數。

并根據RMSE值來計算新一代種群，其計算公式為

(17)

式中:uk,G+1代表第G+1代個體向量；λ為最小容錯率。

3)接著重復進行變異、交叉、選擇操作，當達到所設定的訓練誤差或者達到最大迭代次數時，即可得到最優的輸入權值與隱含層閾值。通過對輸出權值的計算，即可得到用于故障辨識的SADE-ELM分類器。

本文所研究的故障診斷方法流程如圖1所示，采用改進VMD分解與奇異值分解相結合的信號處理方法進行故障特征提取，并采用SADE-ELM分類器用于故障辨識，訓練好的SADE-ELM分類器即可實現電機軸承故障診斷。

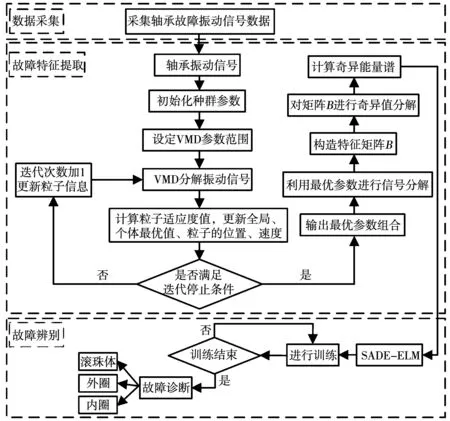
圖1 軸承故障診斷框圖Fig.1 Block diagram of bearing fault diagnosis

3 軸承故障實驗分析

本文的實測數據集來源于美國凱斯西儲大學軸承數據中心[17]。該軸承數據中心采用電機主軸承型號為6205-2RS的深溝球軸承，其相關參數如表1所示。該數據中心通過電火花技術在軸承上人為引入軸承故障，采用電機驅動軸承上方的加速度傳感器進行加速度信號采集，進而得到軸承數據集，其中數據的采樣頻率分為12 kHz與48 kHz兩種。

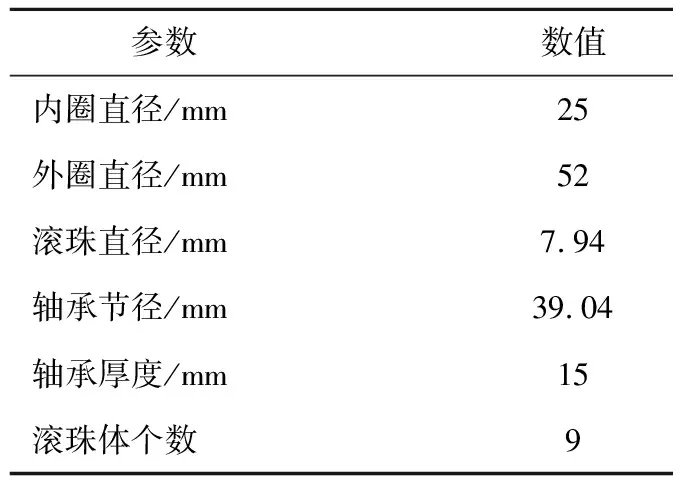
表1 電機軸承參數

本文選擇采樣頻率為12 kHz、不同負載條件下、故障尺寸為0.177 8 mm的軸承故障數據與軸承正常數據作為數據集，來驗證所提出診斷算法的有效性。

3.1 基于改進VMD分解的特征提取

本文采用粒子群算法對VMD參數進行優化以尋求最優參數組合。由于軸承故障種類較多，限于篇幅，以空載時軸承內圈故障時的振動信號為例，振動信號如圖2所示。

圖2 空載時軸承內圈故障振動信號波形Fig.2 Waveform of vibration signal of inner race fault in the case of no-load

通過粒子群算法對VMD參數進行尋優時，其局部極小熵值的變化曲線如圖3所示。

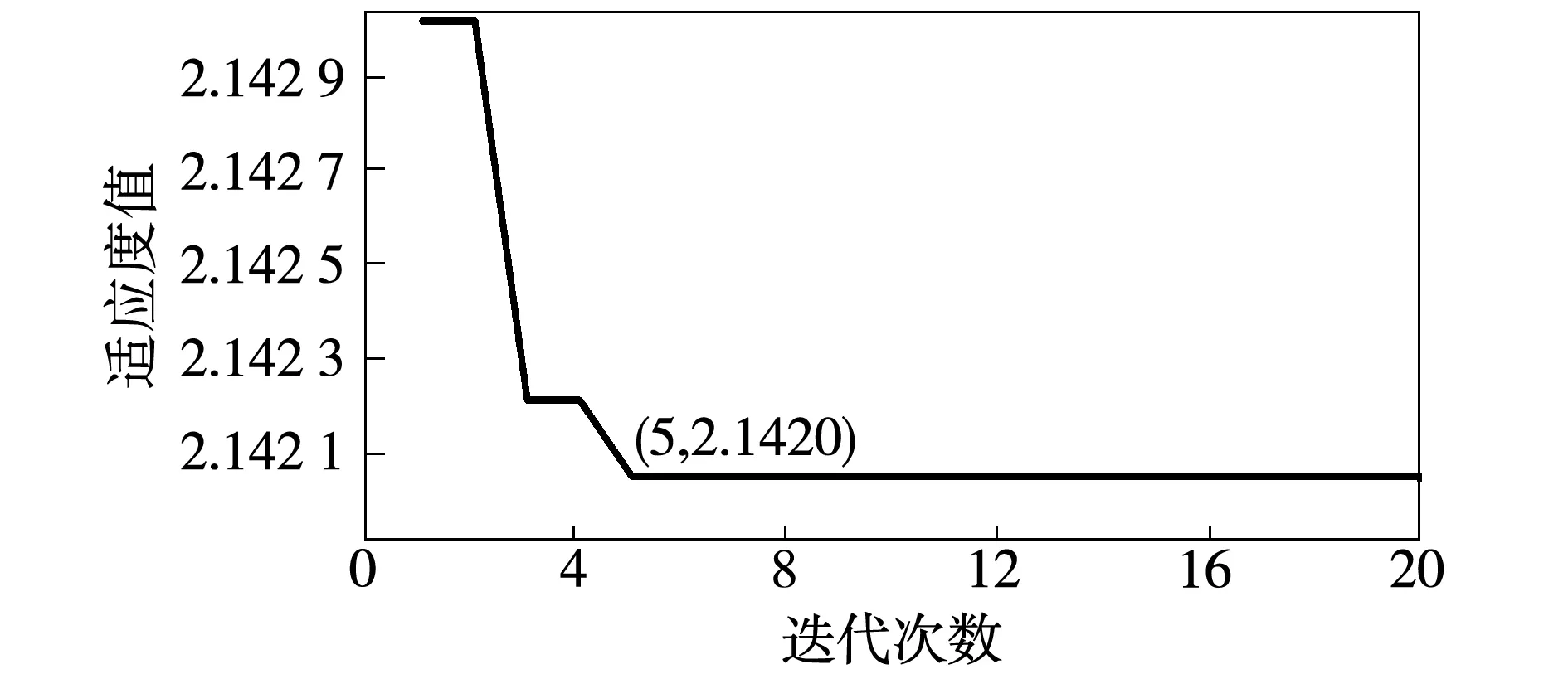
圖3 粒子群優化VMD參數適應度值的更新圖Fig.3 Fitness value update of VMD parameters byusingthe swarm optimization method

由圖3可知，經歷5次迭代，得到局部最小包絡熵值2.142 0。由于故障種類較多，為得到更為精確的分解層數K與懲罰因子α，本文采用了對不同故障時的振動信號進行10次尋優，并求取平均值，最后的得到的最優參數組合(K,α)=(4,162 3)。并利用該參數對軸承內圈故障信號進行粒子群優化VMD分解，得到的IMF分量時頻域波形如圖4所示。

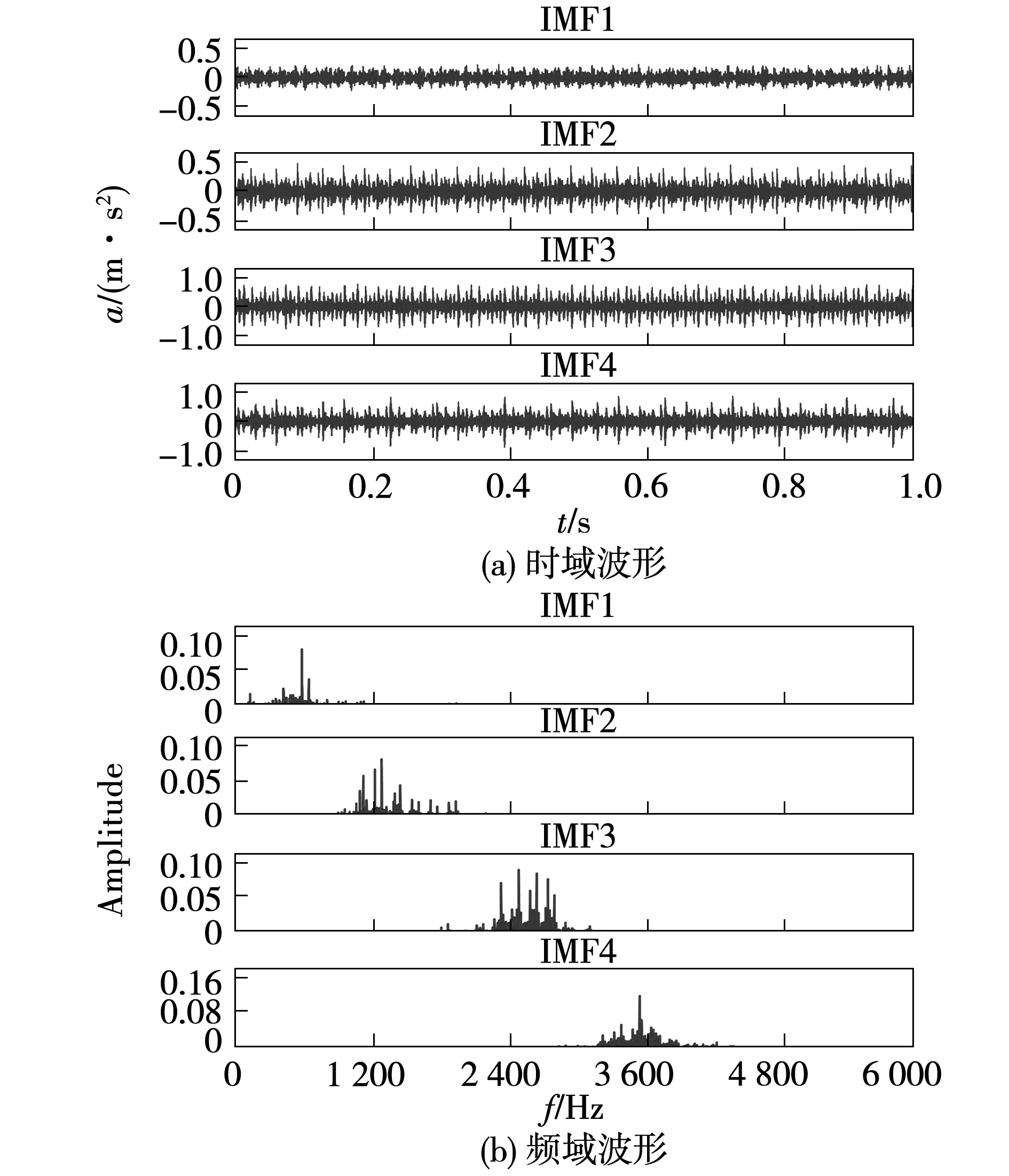
圖4 改進VMD分解得到的IMF時頻域波形Fig.4 Time-domain and frequency-domain waveforms of IMFs obtained by the improved VMD

為驗證所提出方法的有效性，根據中心頻率確定VMD參數的方法，對軸承內圈故障信號進行傳統VMD分解，得到IMF分量的時頻域波形如圖5所示。

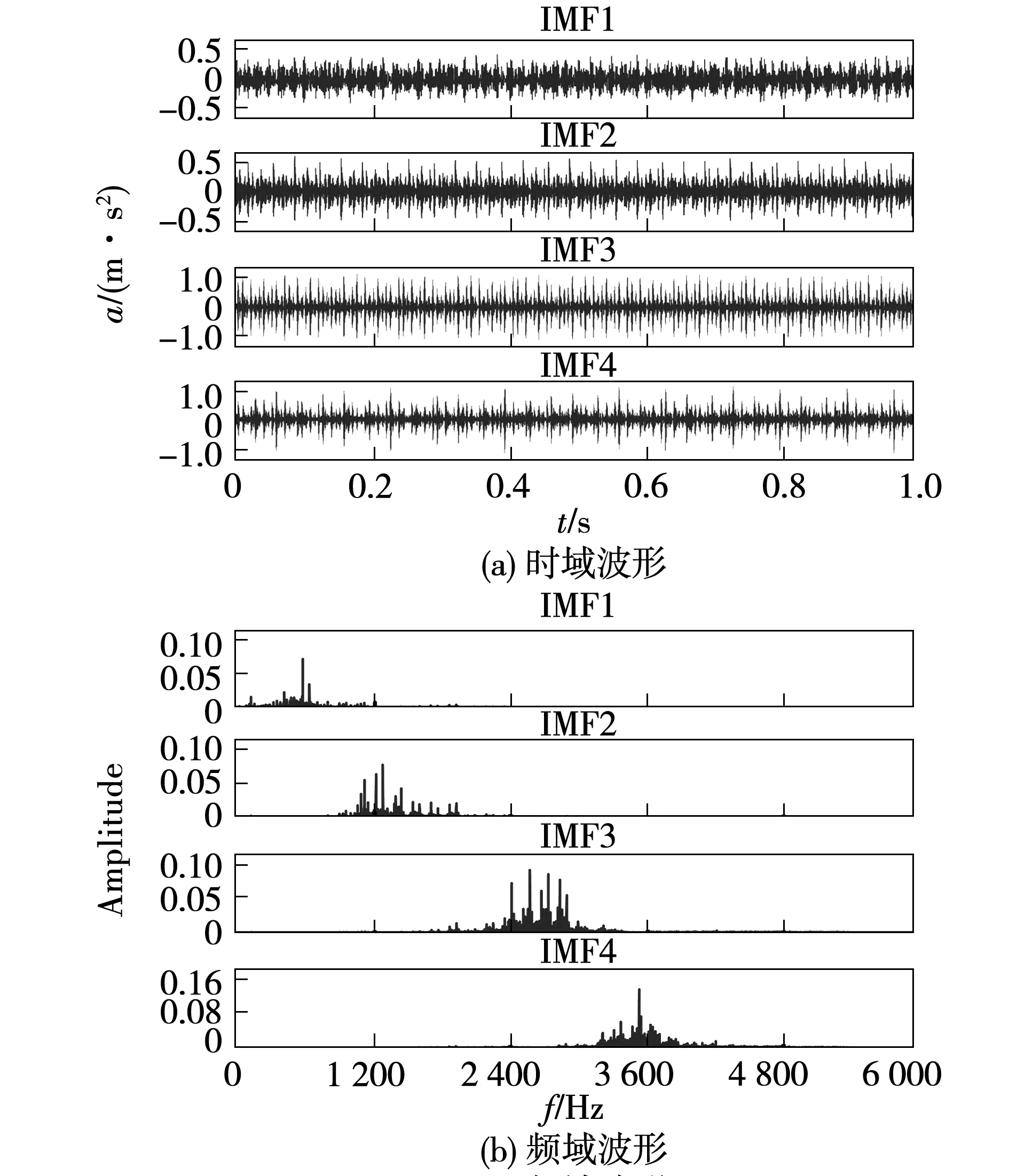
圖5 VMD分解得到的IMF時頻域波形Fig.5 Time-domain and frequency-domain waveforms of IMFs obtained by the VMD

正交性指數(index of orthogonality,IO)與能量保存度(index of energy conservation,IEC)是衡量VMD分解效果的重要參數[18]，其計算公式如下：

(18)

(19)

式中：ci(t)代表分解得到的各IMF；x(t)為原始信號；rn(t)為趨勢項。

IO代表分解得到的各IMF的整體正交性，并且，IO值越小表示各IMF分量的正交性越好，分解精度越高。IEC則表征了信號在分解前后能量的對比度，在信號分解中，IEC值越接近1，說明分解過程中能量泄漏越少，分解效果越好。VMD分解與改進VMD算法的IO、IEC值如表2所示。

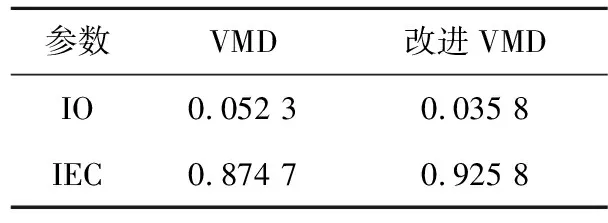
表2 VMD與改進VMD效果比對表

由表2可知，改進VMD分解的IO值更小，IEC值更接近1，表明改進VMD分解得到的各IMF分量整體正交性更好，且分解過程中能量泄漏更少，即改進VMD分解的特征提取效果更好。

在利用改進VMD分解對軸承故障進行分解后，需要根據分解得到的IMF分量構建特征矩陣B，并對矩陣B進行奇異值分解，進而計算出各類故障的奇異能量譜，根據奇異能量譜在不同故障之間的差異可以建立各類故障的特征向量。

3.2 基于SADE-ELM分類器的故障診斷

本實驗一共提取了600組數據，隨機選取500組數據用作訓練集，余下數據作為測試集。在對SADE-ELM分類器進行訓練前需要對種群進行初始化。設置種群數D=100，雜交概率CR=0.6，縮放因子F=0.5，最大迭代次數G=100[19]。在選擇不同的隱含層神經元個數，SADE-ELM分類器的訓練效果也是不同的。模型的訓練精度與隱含層神經元個數的關系如圖6所示。

由圖6可知，隨著隱含層神經元個數的增加，SADE-ELM分類器誤差降低、訓練精度得到提升，但是也會使網絡結構復雜化。當隱含層個數為17時，網絡的訓練精度趨于平穩，繼續增加隱含層神經元個數時，網絡的訓練精度不會明顯提升，還會導致模型過于復雜，故本文選擇隱含層神經元個數為17。

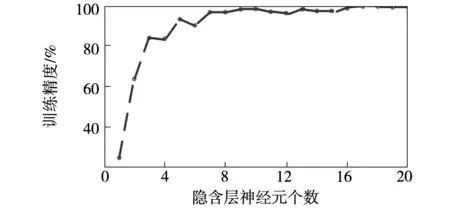
圖6 隱含層神經元個數與分類器訓練精度關系圖Fig.6 Relationship between the number of neurons in hidden layer and training accuracy of classifier

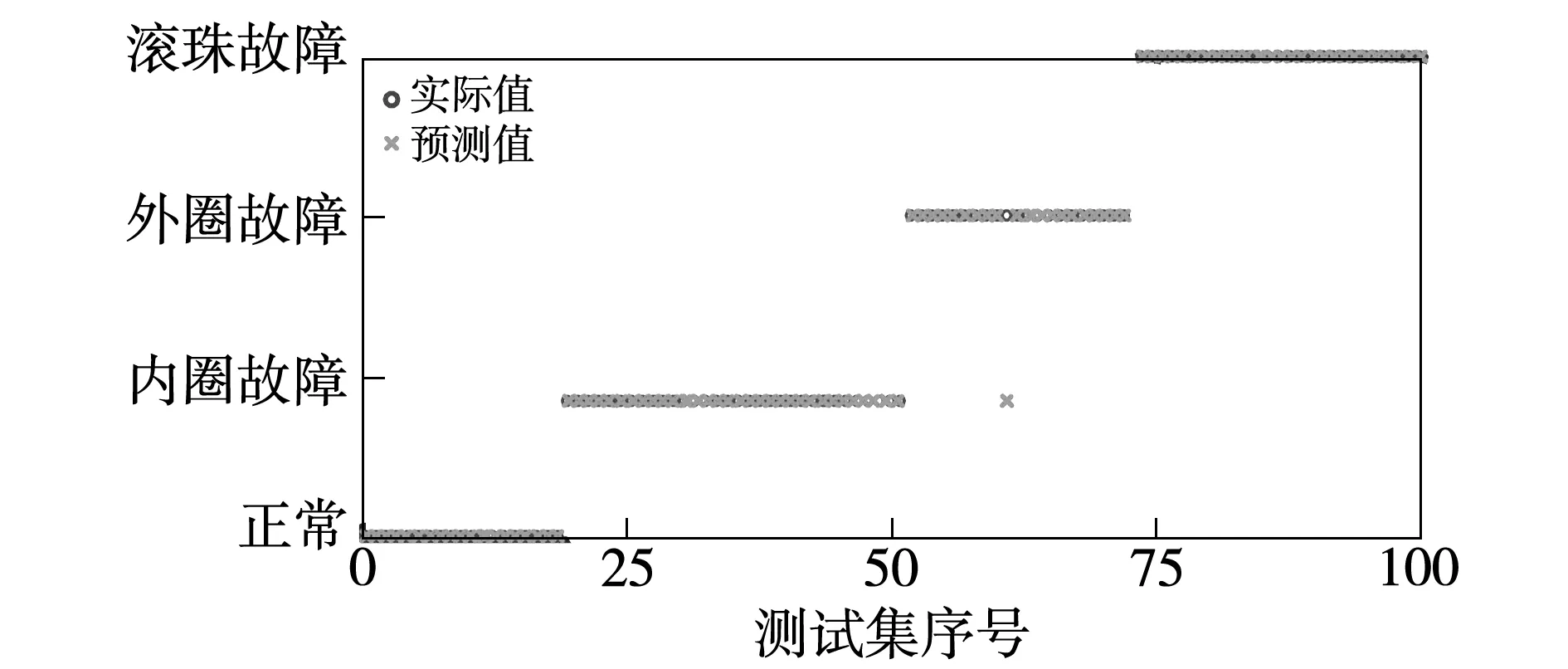
圖7 SADE-ELM分類器分類效果圖Fig.7 Test result of the SADE-ELM classifier

在確定好隱含層神經元個數時，利用測試集數據對SADE-ELM分類器效果進行驗證，驗證結果如圖7所示，為對比SADE-ELM分類器的效果，利用該測試集分別對ELM分類器、DE-ELM分類器進行測試，驗證結果分別如圖8、圖9所示。

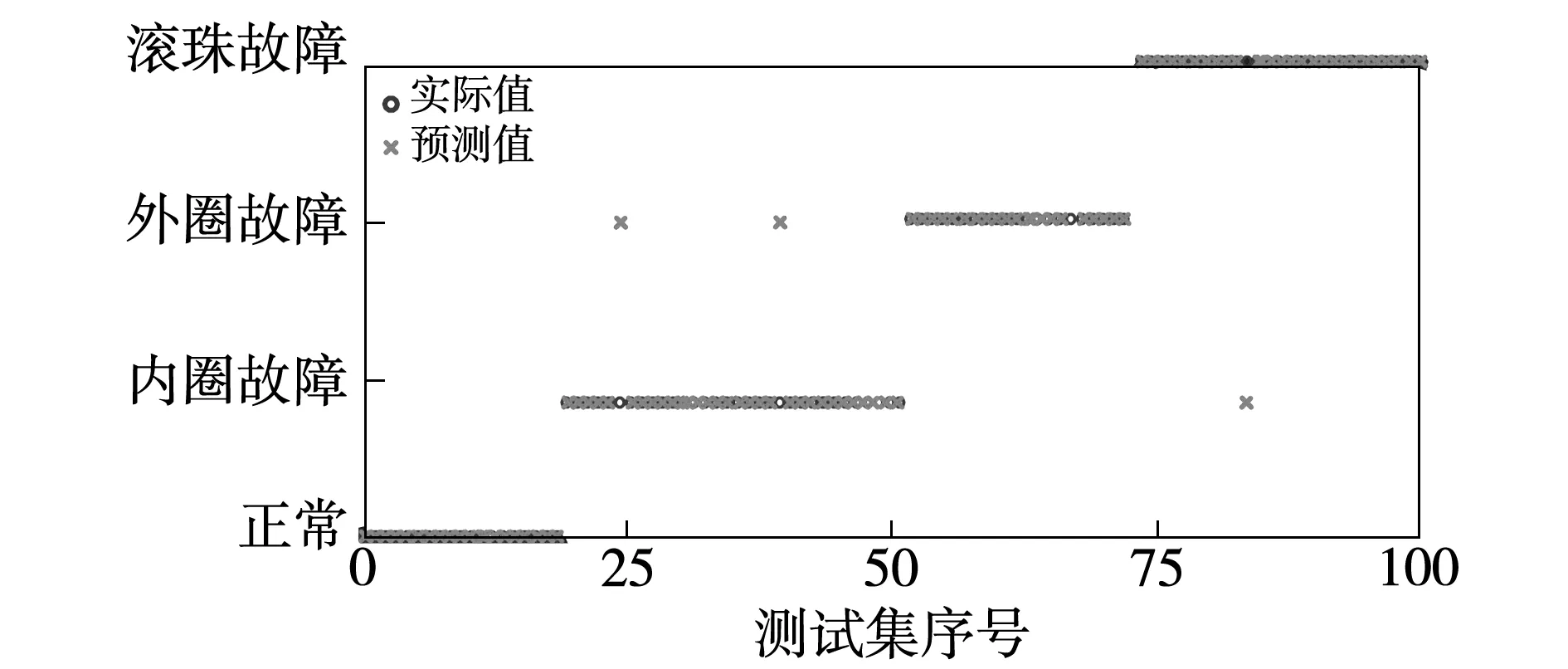
圖8 ELM分類器分類效果圖Fig.8 Test result of the ELM classifier

由圖7～圖9可知，針對于本文測試集，ELM分類器、DE-ELM分類器與SADE-ELM分類器的測試精度分別為96%、98%、99%。為進一步驗證本文所提出的SADE-ELM分類器的分類效果，將相應的數據集進行10次分類測試，并計算平均值，得到的測試結果如表3所示。

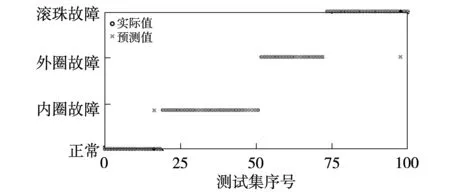
圖9 DE-ELM分類器分類效果圖Fig.9 Test result of the DE-ELM classifier

由表3可知，本文采用的SADE-ELM分類器，相對于傳統的ELM分類器，采用自適應差分進化算法對ELM的輸入權重與隱含層神經元閾值進行優化，使得在訓練過程中均采用最優網絡參數。由實驗結果可知，本文所采用的SADE-ELM分類器由于在訓練過程中進一步對網絡參數進行尋優，網絡的收斂時間相比于ELM分類器、DE-ELM分類器變長，但在訓練集精度與測試集精度上都得到了提升，進而說明SADE-ELM分類器有著更好的分類能力，診斷精度也得到進一步提升。為驗證本文所提出方法的診斷性能，將本文所研究的方法與基于EMD、VMD進行故障特征提取的診斷方法進行比對，其結果如表4所示。

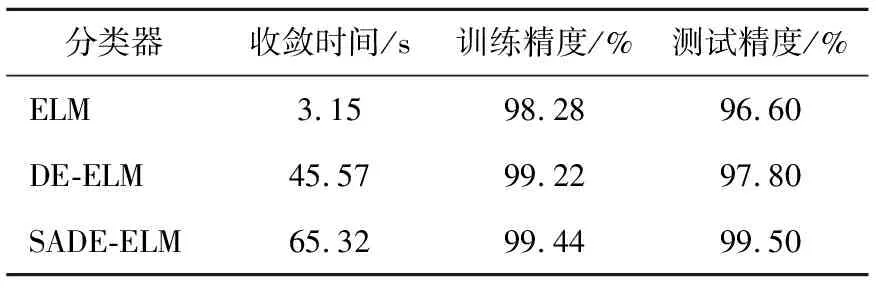
表3 不同分類器測試結果

由表4可知，與基于VMD、EMD算法進行故障特征提取的故障診斷算法相比，本文所提出的軸承故障診斷算法具有更高的診斷精度，驗證了本文所采用的特征提取方法具有更好的特征提取能力。

表4 不同診斷方法測試結果

4 結 論

為解決基于振動信號的異步電機軸承故障診斷存在的振動信號噪聲復雜，故障特征提取困難，診斷精度難以提升的問題，本文研究了一種基于奇異值能量譜與改進ELM的軸承故障診斷新方法并得出如下結論：

1)所研究的方法能夠自適應選擇VMD算法的分解層數與懲罰因子，使得VMD分解效果更優；并將奇異值分解加入故障征提取過程，提高了故障特征提取能力；

2)將自適應差分優化算法融入ELM模型之中，優化了傳統ELM模型的隱含層神經元閾值與輸入權重，提升了ELM模型的泛化能力；

3)雖然所研究方法采用的分類器模型收斂速度較慢，但是分類器的訓練精度與診斷精度均得到提升。