轉矩脈動觸發的牽引逆變器模型預測控制

向超群， 歐陽澤鏗， 成庶

(中南大學 交通運輸工程學院，長沙 410075)

0 引 言

隨著高速列車技術的進一步發展，對牽引系統的性能提出了更高的要求，1985年德國魯爾大學Depenbrock教授提出直接轉矩控制，可以較好的滿足軌道牽引中功率大，開關頻率低的特點[1-2]。然而，由于Bang-Bang控制的特性，可能存在轉矩和磁鏈的高紋波，以及開關頻率不固定等，這也限制了直接轉矩控制的應用。近年來，模型預測轉矩控制(model predictive torque control,MPTC)被引入到電機驅動的高性能轉矩控制中。MPTC與直接轉矩控制相比，直接用精確的模型預測下一時刻電磁轉矩、定子磁鏈等相關變量的變化。通過評估每個電壓矢量的影響，選擇使代價函數最小的電壓矢量，作為下一時刻的輸出，因此，MPTC在矢量選擇方面的準確性和有效性都高于直接轉矩控制[3-7]。傳統的有限集模型預測轉矩控制(finite set model predictive torque control,FSMPTC)雖然具有優越的性能，但由于在一個采樣周期內只使用一個電壓矢量，仍然存在較大的轉矩脈動，這在低采樣率時，尤為明顯。電力牽引由于開關頻率較低，當轉矩偏差過大時，MPTC無法在一個周期內實現無差拍控制[8-9]。

為了提高FSMPTC的性能，許多學者提出了不同的策略。文獻[10]中縮短采樣時間可以獲得滿意的穩態性能，但需要一個更快速的計算平臺，并且會增加系統的成本。利用合成虛擬矢量的方法增加可供選擇的電壓矢量，使FSMPTC具有更大的控制靈活性，從而在穩態下獲得滿意的性能[11-13]。隨著電壓矢量的增多，轉矩可調節的范圍增大，同時轉矩脈動也得到更好的抑制。但與傳統的MPTC相比，計算復雜度大大提高。此外，由于轉矩和磁鏈控制采用精確的轉子角位置，因此這些方法對轉子位置的依賴性很大。

直接轉矩控制(direct torque control,DTC)可以通過在一個控制周期內插入一個非零矢量和零矢量的方法來減小轉矩脈動[14]。這種方法也被引入到改進傳統MPTC的性能中，首先根據成本函數最小化的原則選擇最優的非零矢量。然后，根據轉矩無差拍的原理計算出非零矢量和零矢量的占空比[15-20]。占空比MPTC策略在電機穩態運行時可以獲得更高的控制性能，降低轉矩脈動，但計算量較大，特別是在多步預測或多電平變換器應用中，計算量呈指數增長[17-20]。

為了減少預測中的計算量，文獻[21-28]引入了傳統DTC中的開關表。根據開關表轉矩和磁鏈的偏差輸出，選擇開關表中合適的電壓矢量，雖然需要計算定子磁鏈的位置和扇區，但是這些計算量都十分簡單，相當于減小的代價函數計算量，增加的十分有限[25]。但是相比于傳統的DTC方法，都存在計算量增加的問題。

為了降低不必要的計算支出，同時維持良好的動態響應和穩態性能，本文提出了一種基于轉矩脈動最優的觸發型MPTC。通過分析基于開關表的MPTC，在此基礎上，引入轉矩觸發條件，當滿足條件時，可采用傳統DTC，減少MPTC計算量，當采用MPTC時，可以降低轉矩脈動。

1 牽引異步電動機動態模型

在兩相(α,β)靜止坐標系下，異步感應電機的數學模型可表示為：

(1)

式中：ψs為定子磁鏈矢量；ψr為轉子磁鏈矢量；us為定子電壓矢量；Rs為定子電阻；is為定子電流矢量；ir為轉子電流矢量；Ls為定子電感；Lm為定子電感；ωr為轉子電角速度。

因此，轉子磁鏈可以表示為

(2)

利用前向歐拉法對式(1)與式(2)進行離散，k+1時刻的定子磁鏈與定子電流關系為

ψs(k+1)=ψs(k)+Ts[us(k)-Rsis(k)]。

(3)

(4)

根據定子磁鏈式(3)和定子電流式(4)，可估計出電磁轉矩為

(5)

同時，k+1時刻轉矩預測計算的表達式為

(6)

由式(5)和式(6)可以得出控制周期內轉矩的變化率與電壓矢量的關系，即

(7)

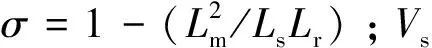
由此可知，隨著定子頻率的提高，零矢量對轉矩減弱的能力增強，正矢量增加轉矩的能力減弱，負矢量增加轉矩的能力也增強。

2 基于開關表的電壓矢量選擇

在一個周期內，傳統的模型預測轉矩控制僅選擇一個電壓矢量，同時，還需要計算代價函數7次。文獻[24]通過選擇相鄰的矢量減少備選的電壓矢量個數，可以通過開關表減少計算量。定子磁鏈的位置表達式為

(8)

如圖1所示，在α-β坐標系中，根據式(9)劃分為6個扇區，每個扇區的電壓矢量開關表如表1所示，即

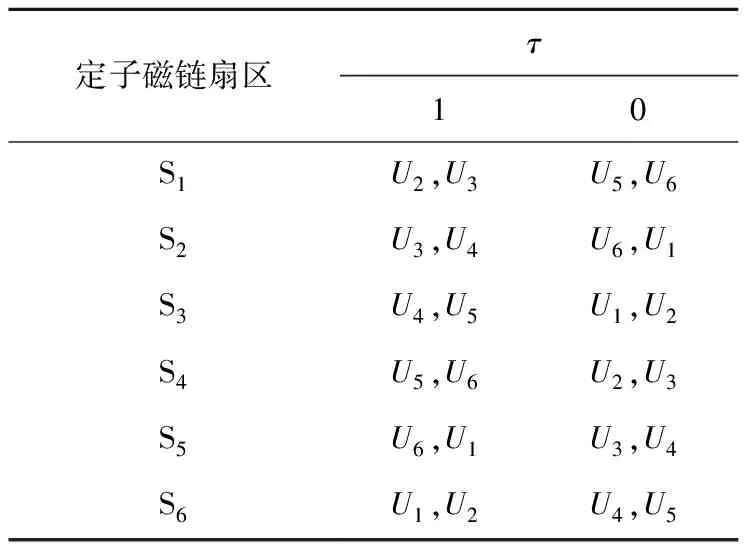
表1 電壓矢量選擇開關表

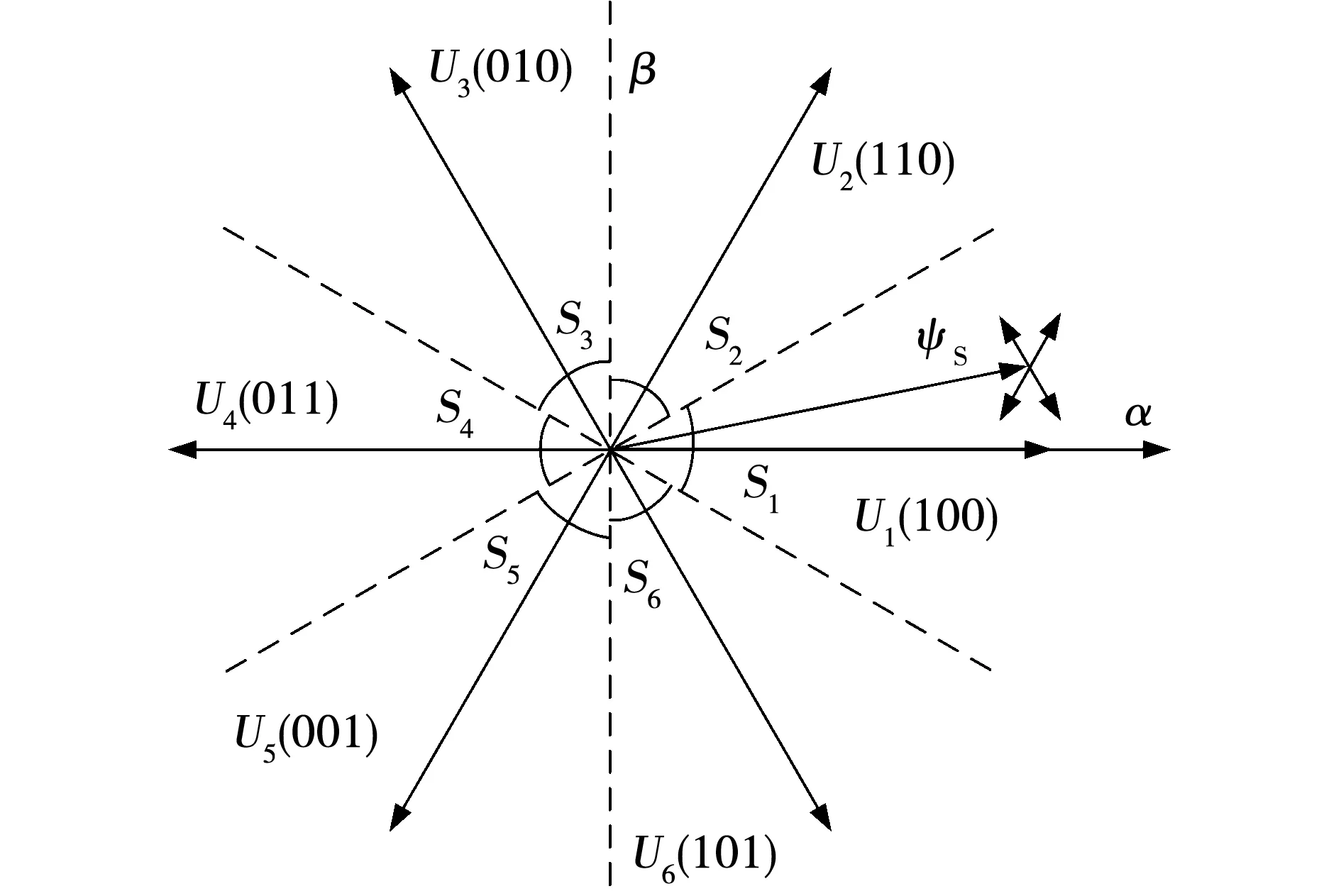
圖1 空間電壓矢量扇區劃分示意圖Fig.1 Diagram of space voltage vector sector

(2N-3)π/6≤SN≤(2N-1)π/6。

(9)

其中SN為扇區編號，N=1,…,6。

在一個周期內電磁轉矩變化率Sj_T表達式為

Te_j(k+1)-Te(k)=Sj_TTs。

(10)

其中，電磁轉矩Te_j(k+1)為電壓矢量uj在k+1時刻的預測量。根據轉矩無差拍控制原則，k+1時刻的輸出轉矩應等于期望轉矩。因此，根據定子磁鏈位置可以選擇最優矢量uopt1和uopt2，可以得到k+1時刻的轉矩和電壓矢量關系為：

(11)

各矢量的占空比計算公式為

(12)

理論上可以實現轉矩的無差拍控制，但是在某些特殊的工況下(如負載突變等)，輸出轉矩無法實時跟蹤響應，此時某個電壓矢量的占空比計算結果將會大于控制周期Ts。因此，需要將每個電壓矢量的作用時間限制在0～Ts之間，即：

(13)

MPTC與傳統DTC相比，具有更好的脈動抑制效果，但是相應的計算量也會增加。因此，可以根據轉矩脈動的需求，選擇不同的控制方式。本文采用轉矩滯環的方法，判斷選擇的控制方式。當預測轉矩位于滯環內，則選擇傳統控制方式，如果超出滯環范圍，應選擇兩矢量MPTC減小轉矩脈動。轉矩滯環的寬度應根據系統所允許的最小脈動值選擇。

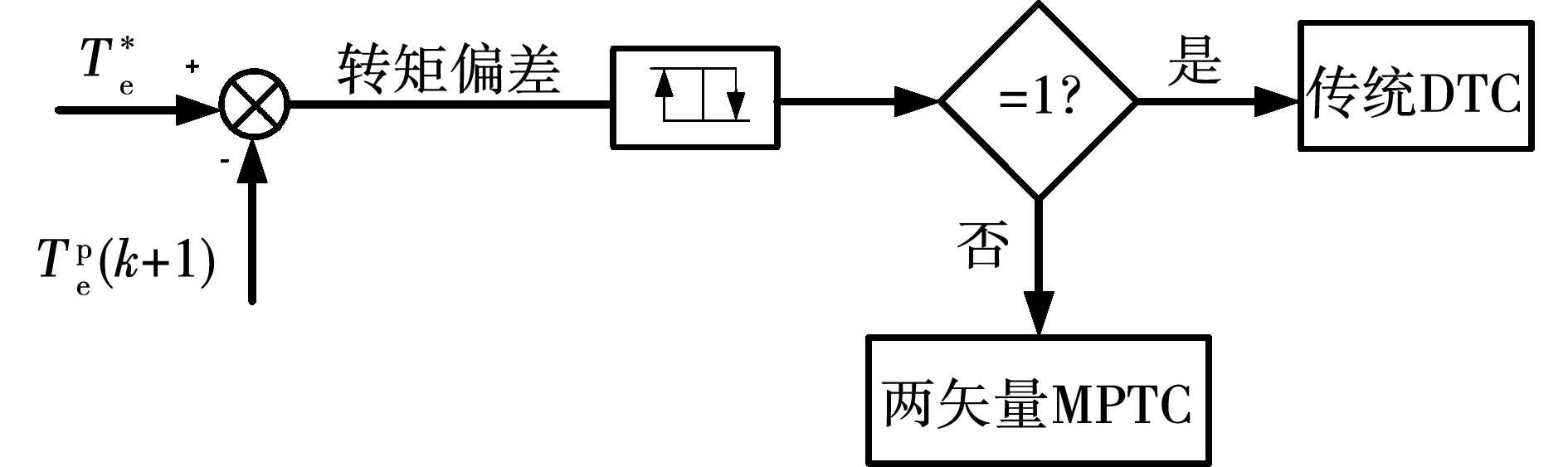
圖2 轉矩觸發條件選擇Fig.2 Diagram of selection triggered by torque

3 基于開關表的兩矢量MPTC

MPTC的主要目標是跟蹤電機的期望定子磁鏈和電磁轉矩。因此，代價函數可構建為

(14)

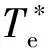
(15)

其中，Ten和ψsn分別為額定電磁轉矩和定子磁鏈。將電磁轉矩、定子磁鏈和二電平逆變器的基本電壓矢量狀態代入到式(15)中，選擇使代價函數最小的電壓矢量輸出。

在離散數字系統當中，計算時間是不可忽略的。在k時刻選出的最優電壓矢量于k+1時刻才會發揮作用，這也就產生了一拍的滯后。如果不對滯后進行補償，則會導致系統的性能下降，定子電流和轉矩誤差增大。為了減小一拍滯后的影響，需要對k+2時刻的電磁轉矩和定子磁鏈進行預測。最優合成矢量uopt1和uopt2用于預測k+1時刻的電磁轉矩Te(k+1)和定子磁鏈ψs(k+1)，同時，兩者也被看作是對k+2時刻進行預測的初始狀態。而且，Te(k+1)和ψs(k+1)用于計算轉子誤差τ和磁鏈扇區。所以，通過計算下式所示的代價函數，使得代價函數最小的電壓矢量作為最優矢量，即

(16)

為了防止電流過大，必須對輸出進行限流，最大電流值Im，必須被包含在代價函數g2當中，即

(17)

因此，最終的代價函數可以表示為

(18)

如圖3所示為本文所提出算法的原理框圖，具體的實施步驟如下。

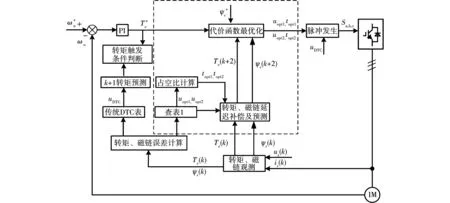
圖3 基于兩矢量開關表原理框圖Fig.3 Scheme of proposed method based on two-vector table

步驟1：測量定子電流和電機轉速，使用公式(1)和(7)估計定子磁鏈和電磁轉矩。

步驟2：轉矩估計的轉矩和磁鏈，分別計算兩者與給定值的偏差。

步驟3：利用計算的偏差，查詢傳統DTC表，得出最優電壓矢量uDTC。

步驟4：根據最優電壓矢量uDTC預測k+1時刻電磁轉矩，并作為轉矩觸發條件的輸入。

步驟5：根據轉矩觸發條件判斷，如果不滿足條件，則需進行虛線框中基于開關表的兩矢量MPTC的計算，如果滿足，則直接選擇傳統DTC開關表輸出uDTC。

以下步驟為根據轉矩觸發條件，需要選擇基于開關表的兩矢量MPTC計算。

步驟6：根據轉矩誤差和文中的表1，選擇合適的電壓矢量，并計算各電壓矢量的對應占空比。

步驟7：預測k+2時刻的定子磁鏈和轉矩。

步驟8：根據代價函數選擇使之最小化的電壓矢量組合，并輸出相應的電壓矢量和占空比。

4 仿真與實驗驗證

為了證明文中方法的有效性，分別對其進行了仿真和實驗的驗證。仿真電機參數采用CRH2型車所用300 kW牽引電機。實驗平臺結構如圖4所示，采用碳化硅二電平逆變器，利用dSPACE模擬控制器運行控制算法，上位機進行數據的顯示和存儲。仿真和實驗采用的參數如表2和表3所示。

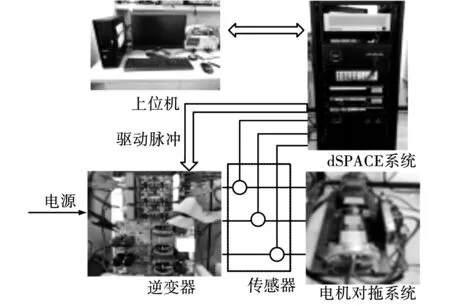
圖4 實驗平臺結構圖Fig.4 Structure chart of experiment platform

已有很多文獻比較了相同條件下MPTC與傳統DTC的性能，本文不再撰述。圖5和圖6分別為兩矢量MPTC方法和本文所提方法DTC-MPTC方法的牽引電機2種不同工況的穩態仿真波形，其中圖5(a)、圖6(a)為轉速2 000 r/min，負載 100 N·m，圖5(b)、圖6(b)為轉速4 000 r/min，負載300 N·m。2種控制方法在轉矩抑制、電流諧波和磁鏈控制均有相近的性能。

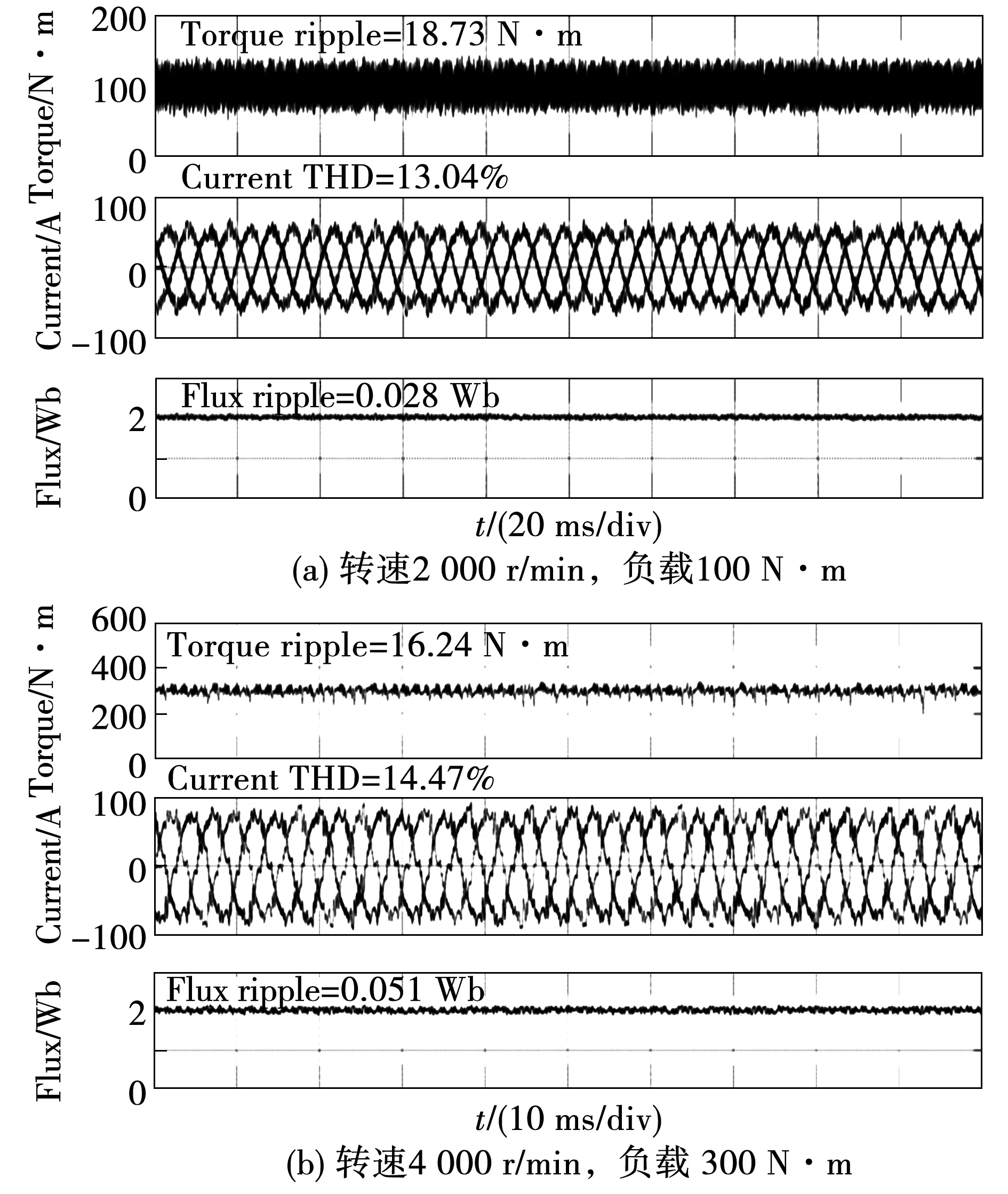
圖5 兩矢量MPTC方法牽引電機穩態仿真波形Fig.5 Simulation waveform of traction motor with two-vector MPTC at steady state

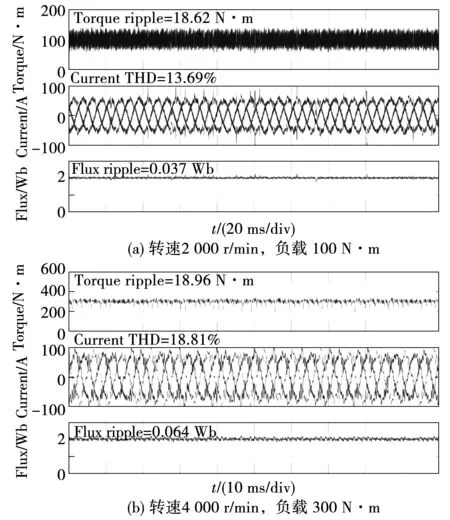
圖6 DTC-MPTC方法牽引電機穩態仿真波形Fig.6 Simulation waveform of traction motor with DTC-MPTC at steady state

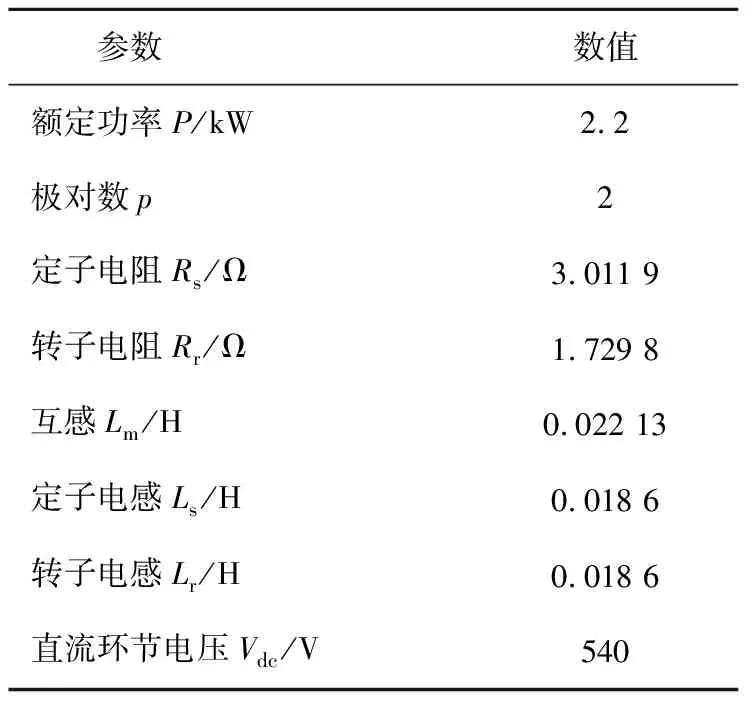
表3 實驗電機參數

圖7為不同速度和負載轉矩時，2種控制方式的作用時間，其中1代表MPTC作用，0代表傳統DTC作用。綜合圖5、6、7可以看出，在低速時，2種控制方法的穩態性能非常接近，因為在低速區域時，由于定子頻率較低，零電壓矢量對轉矩的作用效果較小，在傳統DTC控制中正有效矢量對轉矩的作用效果較強，容易造成較大的轉矩脈動，但是兩矢量MPTC可以利用有效矢量和零矢量合成期望的電壓矢量，實現無差拍控制的目標，因此在低速時，選擇傳統DTC作用的時間較少，約占3%。高速時，由于同等控制周期下，定子頻率提高，正矢量對轉矩的作用效果減弱，傳統DTC方法選擇的矢量引起的轉矩偏差減小，而且零矢量對轉矩的減小作用也隨之增加，采用占空比MPTC方法時，有時無法實現轉矩的無偏差控制，此時可選擇DTC的機會增加，仿真中約占整個高速周期的33%。

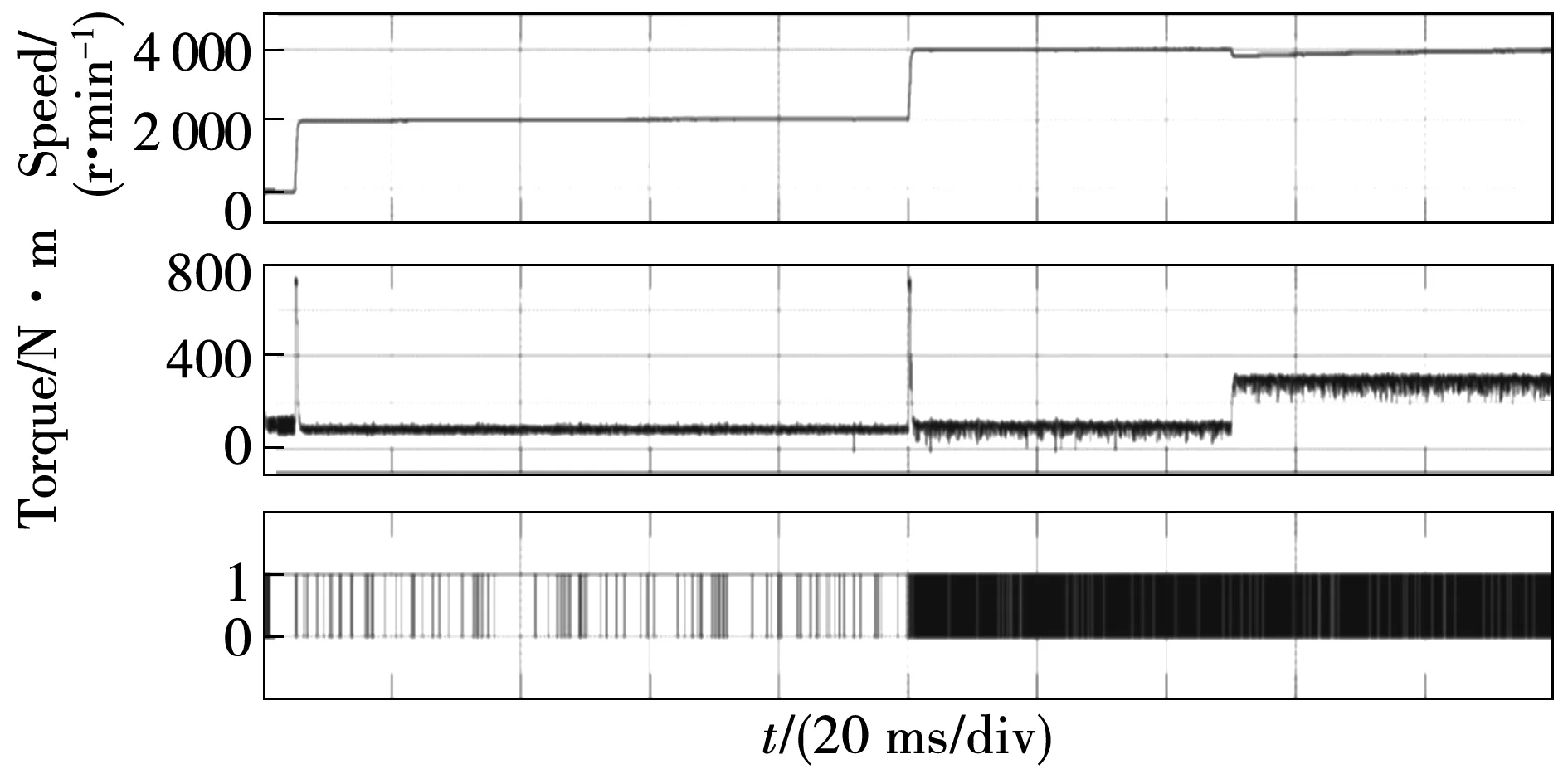
圖7 DTC-MPTC 2種方法占比Fig.7 Proportion of two method DTC-MPTC

圖8為2種控制方法突加負載時的動態響應，兩者均具有良好的動態響應，從100 N·m負載突加到300 N·m的響應時間均約為38 ms。因此新方法沒有降低系統的動態響應速度。

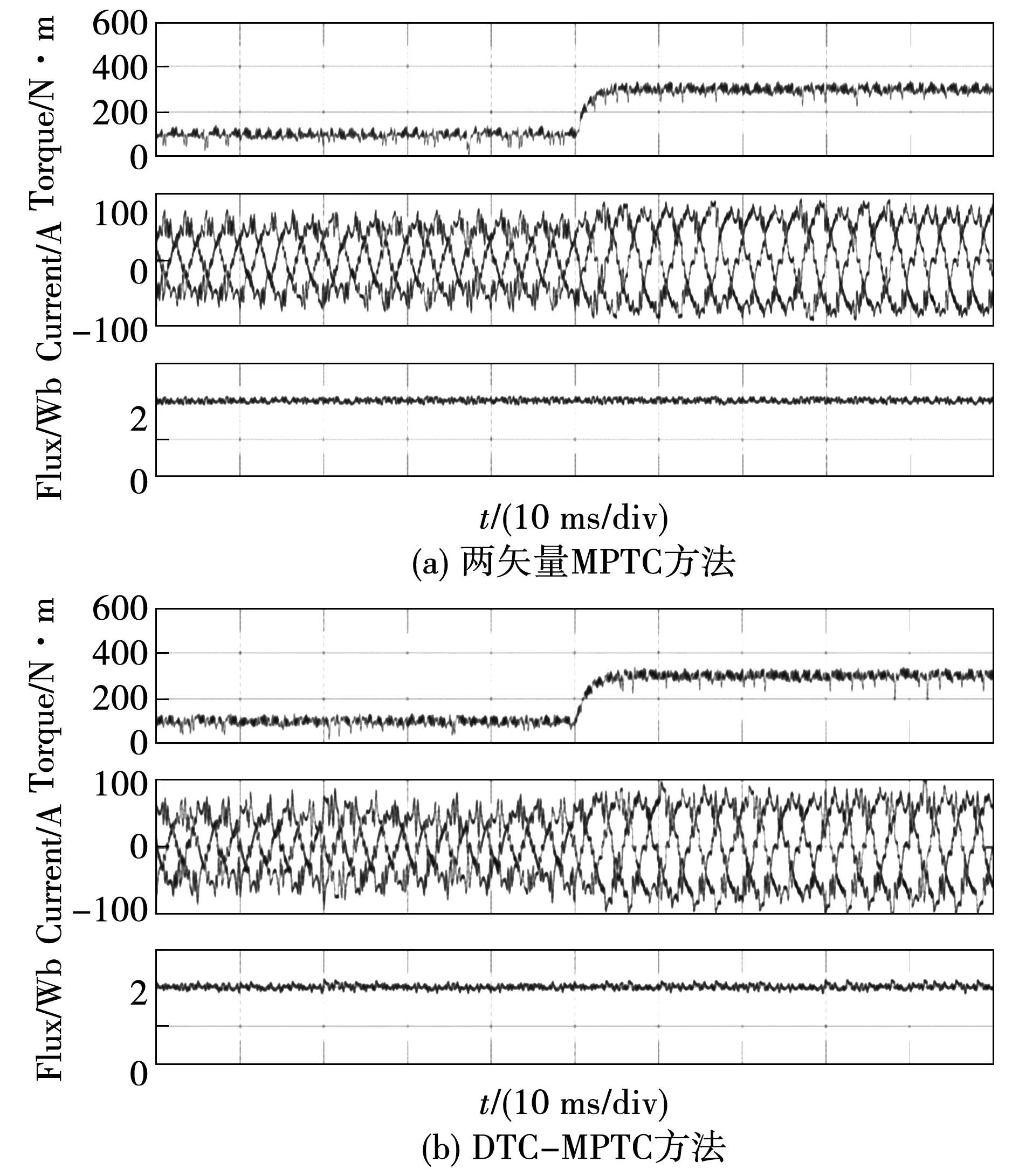
圖8 牽引電機動態仿真波形Fig.8 Simulation waveform of traction motor at dynamic state

為了進一步驗證方法的有效性，在實驗室搭建的2.2 kW電機平臺進行了實驗驗證。圖9為電機從額定轉速1 440 r/min反轉的實驗波形，從圖中可以看出，2種方法都能較好的跟蹤給定，在過渡的時候均未出現較大的尖峰，能順利實現反轉。在轉換時，磁鏈出現了波動，是因為兩矢量MPTC方法在選擇矢量時，優先考慮轉矩的作用，只通過磁鏈權重系數選取矢量。可以通過增大磁鏈權重系數減小過渡時的磁鏈波動。

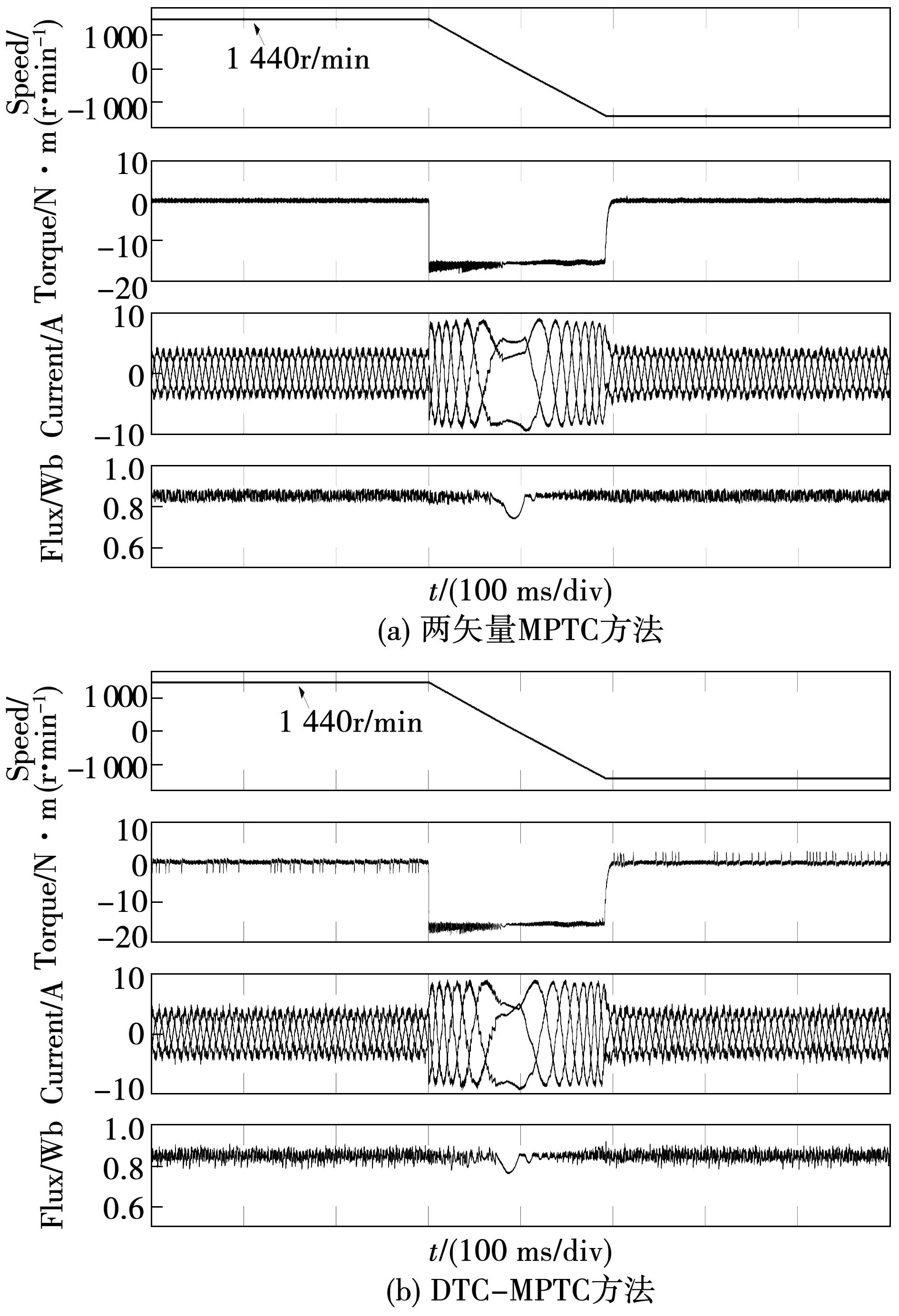
圖9 電機正反轉實驗波形，其中正反轉速度均為1 440 r/min，負載為0Fig.9 Experiment waveform of positive and negative rotation of motor when speeds are both 1 440 r/min and loads are 0

由于在低速時，選擇傳統DTC控制的時間較少，在低速時，DTC-MPTC方法基本等同于兩矢量MPTC，因此，在此不做兩者的對比分析。圖10和圖11分別為2種控制方法在額定轉速時，不同負載的穩態性能，2種方法均能獲得較好的控制性能，雖然DTC-MPTC方法在各項指標中均有微弱的差距，但是可以減小系統計算量，尤其對于絕大部分時間運行于高速區域的高速列車，優勢十分明顯。圖10為2種方法的動態響應實驗波形，兩者均具有較好的動態響應特性，動態響應時間約為5 ms，能跟蹤負載突變。

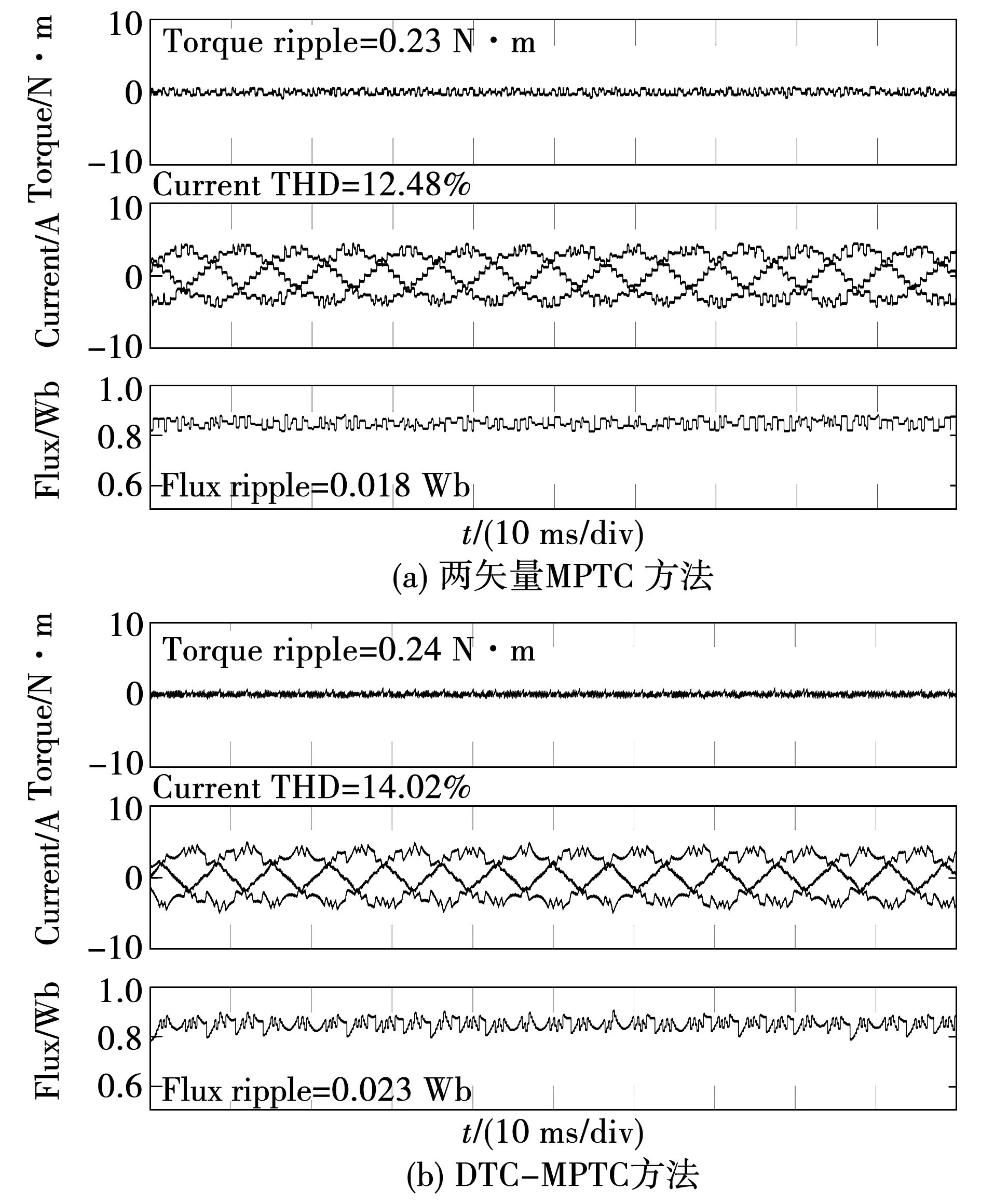
圖10 轉速1 440 r/min負載0穩態實驗波形Fig.10 Experiment waveform of two methods at steady state when speeds are both 1 440 r/min and loads are 0

圖11 轉速1 440 r/min負載14 N·m穩態實驗波形Fig.11 Experiment waveform of two methods at steady state when speeds are both 1 440 r/min and loads are 14 N·m

5 結 論

本文在分析傳統DTC和兩矢量MPTC的基礎上，提出了一種基于轉矩脈動最小的模型預測控制，通過仿真和實驗對比驗證了算法的正確性，并得出如下結論：

1)文中所提出的DTC-MPTC方法在減小轉矩脈動與動態響應、電流諧波以及磁鏈波動抑制等穩態和動態性能方面，均能取得與兩矢量MPTC相近的控制效果，滿足軌道交通車輛運行需求。

2)在高速區域時，DTC-MPTC方法通過轉矩滯環判斷條件，選擇傳統DTC電壓矢量輸出，避免了復雜的代價函數與占空比計算，可以有效減少系統計算量。