提高線上物理教學質量需“鉤玄提要”

包景東

(北京師范大學 物理學系，北京 100875)

“鉤玄提要”系一個漢語成語，意思是探取精微，摘出綱要.其出于唐·韓愈《進學解》:“記事者必提其要，纂言者必鉤其玄.” 直譯為：對待記事一類著作(知識)，一定要提綱挈領，抓住要點；對待立論一類著作(難點)，一定要尋求奧妙，探索精微.有一句掛在嘴邊的話：教學要遵循古代思想家和教育家孔子所言“有教無類”“因材施教”的宗旨.然而，時過境遷，又復忘懷，則教育停滯矣.2020年突發新冠疫情，使得線上教學成為不可或缺的方式，因而需探索新情境下提高教學質量的方略。

首先，讓我們重溫被譽為“教師的教師”的三位大師對物理教研的期許.楊振寧先生比較了中美的教育方式，提到中國傳統教育提倡按部就班的教學方法，這有利于學生打好根基；美國提倡“滲透式”或稱為“體會式”的教育方式，其特點是讓學生在過程中一點一滴地學到許多東西.趙凱華先生認為中美兩種教育方法各有特色，若能將兩者的優點和諧統一起來，則在物理教育上是一個突破.費恩曼先生直白地詮釋了后者：“的確，一個學者在一門課程中所作的全部論證，并不是他從學習大學一年級物理時就記住的.完全相反，他只記得某某是正確的，而在說明如何去證明的時候，需要的話，他就自己想出一個證明方法.無論哪個真正學過一門課程的人，都應遵循類似的步驟去做，而死記被證明是無用的.”

具體而言，費恩曼希望教學要兼顧兩點：一是對于班級中最聰明的學生，試圖使所有的陳述盡可能準確，在每種場合都指出有關公式和概念在整個物理學中占什么地位，以及應該做出修正.二是也希望照顧到另一些學生，對他們來說，這些額外的五花八門的內容和附帶的應用只會使他們煩惱.對這些學生，希望至少有一個他能夠掌握的中心內容或主干材料[1].

以上兩點不失為線上教學的目標.在這種教學過程中，師生互動性難以復制“You Raise Me UP”的場景，但應牢記費恩曼最反對“用字解釋字”的講授方法，此做法未提供給遠程受眾更加有用的信息.就某些概念和定理來說，最好能跳出原來的命題，用生動的實例，用建立“思想實驗”和類比的方法，借助于已知現象來解釋新的現象.在費恩曼看來，這是數學物理學的偉大藝術.顯然，這有賴于師生的知識儲備和批判性思維能力[2].下面，作者以48學時“熱力學與統計物理”的課程實踐，結合著向費恩曼先生學習，談幾點粗淺的認識.

1 問題導向

費恩曼在他巴西講學之旅前，給自己寫下了一個便箋：“首先要搞清楚你為什么要學生學這個專題，以及你要他們知道哪些東西，至于用什么方法，或多或少由常識給出了.”費恩曼所謂的“常識”其實就是完全抓住問題本質的出色技巧.

秉承“沒有問題比問題很多更可怕”的負責精神，線上授課應明確每個章節的動機而不僅是要義，使得同學心中有數，圍繞著核心知識點預習和自學.適用于少課時“熱統”教學，筆者在今年3月14日(π日)出版的文獻[3]中，以【本章提要】的形式，在每章開頭寫出了如下的摘綱：

第一章熱力學基本定律.明確熱力學基本概念，闡述熱力學4個實驗定律及其微觀解讀.已知物態方程計算出3個狀態參數及進行逆運算.基于卡諾定理引入熵，建立可逆過程的三個TdS方程；設計一個準靜態過程計算實際過程的兩態間熵變.

第二章熱力學函數及關系.引入焓、自由能、吉布斯函數等熱力學勢，分析它們的作用.給出選兩個合適自變量的特性函數的微分式，用它們導出四個麥克斯韋關系式；證明可逆過程的一些熱力學等式.還將處理氣體的熱力學規律推廣到其他如表面、磁和電介質、空腔的熱力學系統.

第三章相平衡與相變.首先給出多元復相共存與平衡的相律，著重討論無化學反應的單元二相系的平衡與轉變，即平衡相變.導出兩相共存曲線斜率滿足的克拉珀龍方程，將著重分析范德瓦耳斯氣體的等溫曲線與實驗等溫曲線的行為.

第四章玻耳茲曼統計.導出單個粒子平衡態下所遵守的玻耳茲曼分布，找到系統熱力學函數與配分函數的關系.證明能量均分定理.對雙原子分子組成的理想氣體的量子熱容量進行計算，分析振動和轉動自由度的貢獻，解釋實驗結果.還將玻耳茲曼統計運用到兩能級系統等.

第五章系綜理論.在Γ空間研究粒子平衡態分布，既能處理粒子間相互作用也可以考慮全同粒子不可分辯性.微正則分布是其他系綜分布的基礎，導出與大熱源接觸的固定溫度系統的正則分布，與大熱源和大粒子源接觸的固定溫度和化學勢系統的巨正則分布；分析三種系綜的關系，特別是系綜理論中的1/N!修正因子，從而解決吉布斯佯謬.

第六章量子統計.應掌握量子理想氣體以及滿足的量子統計，有關于自旋為半整數粒子的費米-狄拉克和自旋為整數粒子的玻色-愛因斯坦兩種分布.給出量子統計向經典統計過渡的條件.應用于金屬的自由電子模型引出費米能量的概念；應用于光子和聲子模型，解釋玻色-愛因斯坦凝聚.

2 寓教于例

費恩曼在物理上推崇巴比倫方法而不是希臘方法。作為兩種看待數學的方式，希臘方式是從特別簡單的一組公理出發，導出幾何學的所有定理；巴比倫風格是知道了所有不同的數學定理和它們之間的聯系，但永遠也不完全認識到這些都是能夠從一批公理推出來.在巴比倫的數學學校里，學生們通過做大量的習題來掌握普遍的規則.

1951年末，費恩曼在日本待了幾個星期，主要接待方是日本京都大學湯川(Yukawa)研究所.日方安排費恩曼訪問和參觀了許多機構.費恩曼每到一地，只要有研究物理的人，都會告訴費恩曼他們正在做什么，費恩曼就和他們討論.日本學者先概括介紹他們所研究的一般性問題，然后就寫出一大推公式.

“稍等片刻，”費恩曼說，“這個一般性的問題，有沒有一個特別的例子？”

“怎么沒有？！當然有啊.”

“那好，給我一個例子，我得看例子.”費恩曼接著說：“除非我腦子里有一個具體的例子，看著它怎么演化，否則我是理解不了任何一般性的東西的。”有些人開始時會認為費恩曼遲鈍，以為他不明白那個問題，因為費恩曼問了許多個貌似“傻瓜”的問題.例如：陰極是正的還是負的？陰離子是這樣的還是那樣的？

可是稍后，當日本學者掉進方程式堆里的時候，費恩曼就說：“哪兒有個錯誤！這不可能對！”這個日本人看了看他寫的方程式，過了好一陣子，他果然發現了一個錯誤.他心里犯嘀咕，百思不得其解，費恩曼這家伙兒，一開始聽不明白，可他怎么就能在這么繁瑣的公式中發現這個錯誤呢？

費恩曼暗自得意，“他以為我是跟著他走，推演數學，但我干的不是這個活兒.對于日本人正在努力分析的那個問題，我有一個具體直觀的例子，本能地知道問題的屬性，所以直覺就會告訴我，哪個地方出了錯兒.”因此，費恩曼在日本與物理同行的討論并不愉快.他寫道：“除非他們能給我一個可感覺的例子，但他們大多數人找不出例子，那我就不能理解任何人的工作，不跟他們討論.或者，有些人倒是能給我一個例子，但那個例子非常平凡，你能用一個簡單的方式就解決了問題，為什么還繞了一個大圈子，用復雜的笨方法來說明問題呢？”

由于費恩曼總是不問數學方程式的問題，而是問他們試圖解決的問題的環境.一份在日本科學家中流通的油印小報發表了一篇文章，題目叫做“費的轟炸與我們的反擊.”

3 實驗驅動

費恩曼1949年夏天訪問了巴西，1951年又在那兒待了半年.在里約的巴西大學講授電磁學,學生都畏畏縮縮、不敢發問，令他很失望.他說：“學生學到的只是名詞和抽象的公式，他們可以背誦布儒斯特定律，可是如果問他們，窗外陽光照在海水上，拿起一片偏振片做個簡單實驗，這樣轉和那樣轉會看到什么的時候，他們卻一臉茫然.”考試題目會出：望遠鏡有幾種？學生答得出來，可是卻忽略了望遠鏡的真正意義.遇到諸如此類的事情，費恩曼會大發脾氣，因為他希望能夠嘗試錯誤、發現、自由地探討，而不是灌輸現成的知識.

費恩曼在巴西期間，曾應邀到巴西科學院做過一次關于“談巴西的教學經驗”的演講.他拿起一本被公認寫得非常好的大學物理教材說道：“在這本書里，從頭到尾都沒有提及實驗結果；隨便把書翻開，指到哪一行，我都可以證明書中包含的不是科學，而是生吞活剝地背誦而已.”

舉例來說，把熱力學公式用文字解讀一下等于什么都沒有說.在熱學和熱力學書中，焦耳實驗驗證了理想氣體內能僅與溫度有關，有一個著名的內能公式：

(1)

這個公式出現在《費恩曼物理學講義(第1卷)》中.體會一下費恩曼所不屑的“用字解釋字”是如何解讀的？在等溫條件下，系統內能隨體積的變化，等于定容情況下壓強隨溫度的變化乘以溫度，再減去壓強.若這樣對式(1)進行講解，則它包含了有價值的信息嗎？讓我們學著像費恩曼那樣，一步一步地把此問題能夠揭示的物理告訴學生.

(a) 偏導在物理學上意味等值過程的部分變化率，如何實現熱學中一些常見的等值過程呢？例如：將一個系統與一個大熱源相接觸就可以實現等溫；保持定容的話，你可以想象一個密封的鋼罐；最好辦的是定壓過程，只要將系統與外界相連就可以了.對于像絕熱(adiabatic) 這樣一個普通的概念，只要有發揮的空間或者易被人錯誤理解的地方，費恩曼就不會放過.它是由希臘字母a(不)+dia(穿)+bainein(過)而來的.“絕熱”這個詞在物理上有幾種不同的用法，有時很難看出它們之間有什么共同的含義.

(b) 人們無法直接測量系統的內能以及其他熱力學函數，有些物理量說它有絕對的數值是沒有意義的.所以將熱力學函數表示成物態參量T、p和V的函數，然后再測量它們相對某種變化的變化.

(c) 教師要向學生提供的最大幫助是，從課程中總結出一些解決問題的規律來，比如證明可逆過程中的熱力學等式，就有基本的套路可循：數學上寫出二元函數的全微分，物理上熱力學第一定律和第二定律相結合；將兩個方程中的自變量轉化為相同，對應項相等；再利用麥克斯韋關系式，最后抵達結果.

(d) 大部分人學習熱力學難免的經歷是：裝懂→不懂→真懂。這里的“真懂”不是停留在抽象的公式上，而一定是你將基礎知識運用到了具體的物理過程，這才是費恩曼的風格！

有一位學生發微信問作者：“內能公式的結論是，在溫度保持不變的情況下，若理想氣體的體積發生變化時，則它的內能不變.是否存在一個公式，可以用來驗證理想氣體的焓不隨壓強的變化而改變？”出自于學生的好問題！筆者在期中測驗中出了如下的題目：

物性均勻的系統存在一個內能公式，那么對焓H而言，類似的公式具有形式：

(2)

(i)寫出A和C的表達式；(ii)嚴格證明這一公式；(iii)討論構造這一公式的出發點，并舉例說明其正確性。

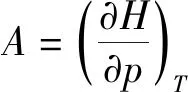
4 演繹歸納

費恩曼先生認為學習物理有5個方面的理由，其中他所列的第三個學習物理好處是：認識自然的美妙，感受世界的穩定性和實在性.新冠疫情給世界造成了不穩定性，同學們安靜地跟隨著我們教師線上學習，體現出網課的實在性.最后，作者對課程進行總結，將核心知識點鏈接起來[3]：

一、平衡態熱力學：以幾條實驗定律為框架的傳統熱力學亦稱為經典熱力學.溫度、能量和熵構成了這一學科的三大要素.

1) 溫度在第零定律以熱接觸方式被定義了，也出現在另3條定律之中，它是區別于力學平衡的一種運用的非常廣泛的熱平衡和熱漲落的標志.

2) 熱力學第一定律將兩種相互作用能(功和熱量)的變化與體系內能(總能量)增減聯系在一起.第二定律的重要成果是建立了一個態函數熵(熱溫比)，它限制了實際過程的進行方向，現如今來看這一概念比能量更為重要.

基于熱力學第一與第二定律的結合以及態函數存在全微分的條件，可以研究均勻物質的熱力學函數的關系.為了用態函數的差來方便計算某一可逆等值過程的功和熱量這兩個過程量，也為了判斷在某個量保持不變前提下，不可逆過程的進行方向，引入了一些態函數，關鍵是記住特性函數的兩個自變量.特別注意：表面系統和電磁介質等廣義功與氣體的體積功相差一個負號，這是因為凝聚態體系必須外界對它們做功.

3) 熱力學第三定律(也稱能斯特定理)表明當熱力學溫標趨于零時，熵等于零，也告訴人們絕對零度的不可被達到.對于熱力學態函數(內能、自由能、焓和吉布斯函數)而言，僅有差才有意義，惟有熵常數在極限零溫被確定了，即存在絕對熵概念.

4) 相平衡和轉變是經典熱力學最成功應用的范例.兩相共存時的壓強與溫度函數關系為相平衡方程，該曲線的斜率遵守克拉珀龍方程.任何氣體物態方程都不能描寫氣液兩相共存的情況，需要實驗測量繪出等溫曲線.不過，我們以范德瓦耳斯氣體為例，在p-V圖上畫出等溫曲線，利用兩相化學勢相等理論要求，氣液共存的水平直線段使上下曲線與該直線所圍面積相等，此即麥克斯韋法則.

二、統計熱力學：以玻耳茲曼公式(熵與微觀態數關系)為導引的熱力學理論現被叫做統計熱力學，牛頓力學和統計分布律同時起作用.它是信息論的出發點.牛頓力學并沒有時間之箭，熱力學中的時間之箭從何而來呢？玻耳茲曼又是如何從無時間之箭的力學結構中無中生有地得出一個時間之箭呢？熱力學第二定律中的時間之箭產生于兩個方面：

① 初始條件與平衡狀態之間相差一個很大的、宏觀上可探測到的量，一個朝熵增加方向演變的狀態，它必定不是一個其存在只能通過微觀方式才能觀察得到的極其微小漲落.

② 尋求的是系統在一個特殊條件之后的演變，這一條件由外部方式而非通過孤立系統自然發展而得到.當然還有概率性和馬爾科夫過程的解釋.

三、平衡態統計分布律：平衡態統計物理的基本假設只有一條：平衡態下的孤立系統的各個微觀態出現的概率相等.統計物理的兩種最基本手段是最概然統計和系綜理論，都用到了等概率統計假設.前者利用了平衡態最為無序，則所對應的微觀狀態數最多；后者將系統加環境視為一個孤立系統，進而總分布密度函數為一常數.

1) 最概然統計的物理思想生動.以定域可分辨的單個粒子為研究對象，事先在任一能層內將μ空間化分成許多小相格，這樣一來就可以計算微觀狀態數目，在近獨立近似條件下，求出使微觀態數極大的宏觀粒子分布.玻耳茲曼統計應用到氣體量子熱容量、兩能級系統的負溫度和相對論氣體等情形取得了滿意的結果.

2) 系綜理論方法令人生趣.構造出由N個存在相互作用的粒子組成的正則系綜和巨正則系綜，前者系一個系統與一個大熱庫接觸；后者的系統不僅與一個大熱源而且還與一個大粒子源相接觸.整個系統加環境為一孤立系統.大熱源的性質對系統行為沒有影響，因此可以假設其是由單原子分子組成的理想氣體.從而對聯合密度函數中的熱源變量積分，而獲得關于系統變量的分布密度函數.

在系綜理論中，也可處理無相互作用的理想氣體分子，在計算微觀狀態數時，相同粒子在不同相格中交換不產生新的微觀態，即僅考慮粒子組合引起的狀態數而不認為不同的排列帶來新微觀態.相對于玻耳茲曼統計計算的微觀狀態數，須乘以吉布斯修正因子1/N!.最初它是作為量子修正引入到經典統計中，而現在它是自然而然地進入到熱力學公式中，因為它保證了自由能、熵和吉布斯函數等三個熱力學函數的可加性或廣延性.歷史上用系綜理論成功地解決了吉布斯佯謬，從此以后這一理論被應用于許多領域.

3) 分布密度函數的歸一化系數的倒數就是系統的配分函數，諸熱力學函數和物態方程可以通過對配分函數的求導和取自然對數而得到；兩種方法給出相同的熱力學函數與配分函數的關系公式.

四、量子統計：任何微觀粒子的重要特征是具有自旋，要么是整數自旋的玻色子，要么是半整數自旋的費米子(遵守泡利不相容原理).在統計物理范疇內，量子粒子區別于經典粒子在于：全同粒子的不可分辨性和能級的離散化.物理上凡是不能用經典處理的系統稱為簡并系統，這是因為量子粒子均有自旋角動量自由度，能級相同但還是其他自由度不相同.量子統計學不是完全的量子力學，卻成功地解決了能均分定理計算的雙原子分子理想氣體的定容熱容量在低溫與實驗不符的困難；在高溫、低密和重粒子質量情況下，即簡并退化，系統可以用經典統計來處理.

費米-狄拉克和玻色-愛因斯坦統計反映了單粒子態所能填充的平均粒子數對能級和化學勢的依賴關系.在T=0 K極限下有解析解，我們在動量空間發現了新的物理量和現象，例如：費米面、玻色-愛因斯坦凝聚等.兩個量子統計精確可解的問題是：(i)自由電子氣或金屬晶格模型；(ii)光子氣和輻射場模型.

5 結語

本文依照古人＂鉤玄提要＂的智慧，借鑒諾貝爾物理學獎獲得者費恩曼的方法，對《熱力學與統計物理》課程的線上教學進行了探索.總結出問題導向—生動案例—提綱挈領的實施方案.希望與同行分享討論，推進這門在本科物理諸多課程中可謂“內容繁難、思想深刻、綜合性強”的建設.