差異六面體網(wǎng)格模型間數(shù)據(jù)映射傳遞研究
劉 安,胡廣旭,苗玉剛,鞏慶濤
(1.哈爾濱商業(yè)大學(xué)機(jī)械系,黑龍江哈爾濱 150028;2.哈爾濱工程大學(xué)船舶工程學(xué)院,黑龍江哈爾濱 150001;3.魯東大學(xué)蔚山船舶與海洋學(xué)院,山東煙臺(tái) 264025)
近些年來,由于制造行業(yè)對(duì)智能制造與數(shù)值模擬技術(shù)的廣泛認(rèn)可,制造工藝鏈模擬技術(shù)也隨之誕生。制造工藝鏈模擬技術(shù)是工藝模擬技術(shù)向多工序制造流程的延伸。隨著工藝模擬研究的逐漸深入,采用多工藝制造的復(fù)雜零部件在不同工藝下的物理化學(xué)作用以及相互影響,漸漸受到工藝研究者的重視。歐洲先進(jìn)制造領(lǐng)域研究者首先探索了制造工藝鏈模擬技術(shù)的相關(guān)研究。針對(duì)汽車結(jié)構(gòu)制造優(yōu)化問題,Papadakis L 等基于有限元方法開展了車體薄板結(jié)構(gòu)沖壓、焊接以及強(qiáng)度與碰撞計(jì)算的連續(xù)模擬,系統(tǒng)地分析了各工藝環(huán)節(jié)對(duì)結(jié)構(gòu)制造最終質(zhì)量的影響,進(jìn)而全面協(xié)調(diào)各工藝環(huán)節(jié)進(jìn)行整體優(yōu)化,提高了產(chǎn)品的綜合制造性[1]。Alexander Govik,Zaeh 等進(jìn)一步開展了輕質(zhì)合金的成形與焊接制造工藝鏈模擬研究[2-3]。在此基礎(chǔ)上,為了保證工藝模擬數(shù)據(jù)傳遞,Afazov 開發(fā)了用于不同有限元計(jì)算軟件之間的數(shù)據(jù)格式轉(zhuǎn)換系統(tǒng)FEDES[4],并實(shí)現(xiàn)航空發(fā)動(dòng)機(jī)圓盤組件的制造工藝鏈模擬,以保證應(yīng)力應(yīng)變數(shù)據(jù)在不同制造工藝模型間的繼承與傳遞,進(jìn)而實(shí)現(xiàn)了熱處理、機(jī)械加工、噴丸處理等多種工序的制造工藝鏈模擬[5]。然而,盡管上述制造工藝鏈模擬技術(shù)可以“透視”整個(gè)制造過程,但實(shí)現(xiàn)制造工藝鏈模擬需有效地將有限元模擬數(shù)據(jù)在不同工藝模型間進(jìn)行映射與傳遞,Afazov 相關(guān)程序代碼尚未公開和商業(yè)化,限制這項(xiàng)技術(shù)進(jìn)一步普及應(yīng)用。因此,國(guó)內(nèi)連續(xù)模擬仍處于單工藝連續(xù)模擬階段,主要用于板料塑性成形工藝優(yōu)化研究[6-7]。其中限制這項(xiàng)技術(shù)普及應(yīng)用的關(guān)鍵問題是不同工藝模擬間的數(shù)據(jù)映射與傳遞技術(shù),尤其是采用形函數(shù)法實(shí)現(xiàn)差異六面體網(wǎng)格間數(shù)據(jù)傳遞時(shí),需求解非線性方程組,涉及迭代循環(huán)計(jì)算,計(jì)算數(shù)據(jù)量大,限制了該項(xiàng)技術(shù)的普及應(yīng)用[8]。因此,文中將在前期研究基礎(chǔ)上[9-10],通過直接計(jì)算方法代替迭代循環(huán)計(jì)算,實(shí)現(xiàn)了差異六面體網(wǎng)格的有效數(shù)據(jù)映射,并開發(fā)其用戶程序。
1 差異網(wǎng)格數(shù)據(jù)映射技術(shù)
開展制造工藝鏈模擬時(shí),為了保證模擬物理數(shù)據(jù)在不同工藝階段數(shù)值模型的連續(xù)性,需將前道工序的模擬結(jié)果數(shù)據(jù)傳遞至后道工序的模型中。如果前后工序采用不同網(wǎng)格模型,還需將模擬結(jié)果數(shù)據(jù)映射至后道工序網(wǎng)格模型對(duì)應(yīng)網(wǎng)格節(jié)點(diǎn)。常用差異網(wǎng)格間的映射插值技術(shù)有最近點(diǎn)法、點(diǎn)場(chǎng)距離法、單元距離法及形函數(shù)法[4]。其中,形函數(shù)法符合有限元網(wǎng)格原理,傳遞精度最高。該方法利用有限元單元形函數(shù)將單元節(jié)點(diǎn)的結(jié)果數(shù)據(jù)插值獲得單元內(nèi)任意位置點(diǎn)的結(jié)果數(shù)據(jù)。
如式(1)所示,其中Dp為單元內(nèi)任意點(diǎn)P的結(jié)果數(shù)據(jù)值(應(yīng)力、應(yīng)變或位移)。

Di為單元節(jié)點(diǎn)上的結(jié)果數(shù)據(jù)值,ηi為Di相應(yīng)的形函數(shù)參量。
計(jì)算8 節(jié)點(diǎn)的3D 六面體網(wǎng)格內(nèi)任意點(diǎn)P的數(shù)據(jù)值時(shí),其形函數(shù)如式(2)[4]。

預(yù)求解六面體網(wǎng)格單元內(nèi)任意點(diǎn)P對(duì)應(yīng)映射局部坐標(biāo)點(diǎn)(g,h,r)位置時(shí),需求解式(3)的非線性方程組[4]。
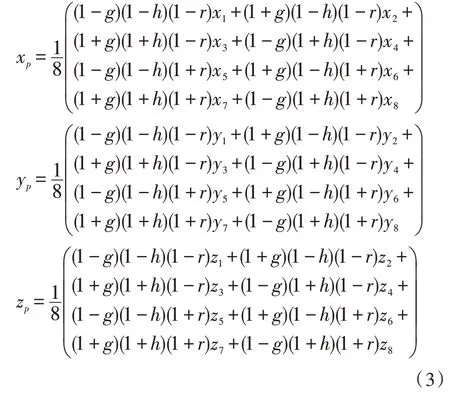
此時(shí)計(jì)算式(3)時(shí),需采用牛頓拉夫森進(jìn)行循環(huán)迭代計(jì)算,且計(jì)算的精度取決于收斂精度。但采用上述方法實(shí)現(xiàn)三維六面體網(wǎng)格的差異網(wǎng)格數(shù)據(jù)傳遞時(shí),求解局部坐標(biāo)點(diǎn)(g,h,r)位置增加了網(wǎng)格傳遞循環(huán)計(jì)算量。
2 形函數(shù)法有限元數(shù)據(jù)傳遞算法流程
如圖1 所示網(wǎng)格模型A 的節(jié)點(diǎn)數(shù)據(jù)傳遞至模型B 時(shí),其算法流程為:
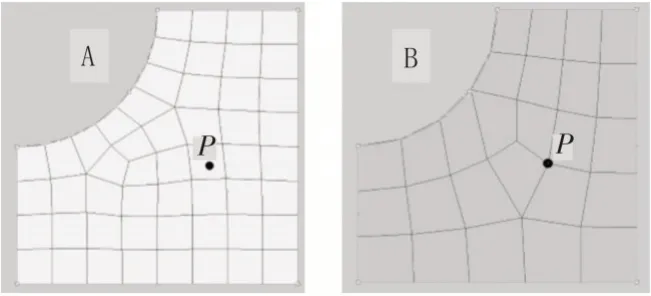
圖1 數(shù)據(jù)映射的差異網(wǎng)格
1)在模型B 中循環(huán)獲取任意節(jié)點(diǎn)的全局坐標(biāo)值,即為P(x,y,z);
2)查找P(x,y,z)點(diǎn)在模型A 中所在單元EAi;
3)獲取單元EAi的節(jié)點(diǎn)坐標(biāo)數(shù)據(jù)Nj(x,y,z);
4)基于單元形函數(shù),求解非線性方程組,如式(3),獲得P(x,y,z)點(diǎn)的局部坐標(biāo)映射值P(g,h,r);
5)在模型A 的模擬結(jié)果數(shù)據(jù)(應(yīng)力、應(yīng)變、溫度等)中查找單元EAi的節(jié)點(diǎn)或積分點(diǎn)結(jié)果數(shù)據(jù);
6)采用形函數(shù)插值法,如式(2),通過單元EAi的節(jié)點(diǎn)模擬數(shù)據(jù),計(jì)算獲取P(g,h,r)的插值映射值DP;
7)步驟循環(huán)1)~6),直至獲取模型B 中所有節(jié)點(diǎn)的模擬數(shù)據(jù)值,退出循環(huán)。
按照上述算法[11-13],實(shí)現(xiàn)差異網(wǎng)格數(shù)據(jù)傳遞時(shí),算法總循環(huán)為模型B 的總數(shù)CNB,傳遞其每一個(gè)節(jié)點(diǎn)數(shù)據(jù)時(shí),都要循環(huán)獲取EAi,對(duì)于六面體網(wǎng)格為8節(jié)點(diǎn),此時(shí)計(jì)算所需循環(huán)數(shù)為CEA×8;進(jìn)行算法步驟4)時(shí),求解非線性方程組進(jìn)行牛頓拉夫森迭代時(shí),仍需循環(huán)計(jì)算,循環(huán)數(shù)為nC,取決于迭代步長(zhǎng)和收斂精度;獲取模型A 指定單元EAi模擬結(jié)果數(shù)據(jù)時(shí),仍需進(jìn)行循環(huán)A 單元數(shù)次εCEA,ε表示當(dāng)獲取指定單元后剩余單元數(shù)無需循環(huán)的系數(shù),0<ε<1,可近似為0.5。基于上述可知總算法循環(huán)數(shù)為式(4):
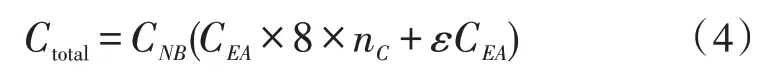
假設(shè)模型A 六面體網(wǎng)格數(shù)量為10 萬,網(wǎng)格B 節(jié)點(diǎn)數(shù)量為7 萬,假設(shè)牛頓拉夫森循環(huán)數(shù)平均為50 次,此時(shí)總循環(huán)數(shù)按上式計(jì)算為2.803 5×1012次,且在每個(gè)循環(huán)下都進(jìn)行大量空間計(jì)算,因此網(wǎng)格數(shù)據(jù)傳遞計(jì)算時(shí)間較長(zhǎng)。數(shù)據(jù)傳遞的算法中,針對(duì)模型A 與B 的循環(huán)是不可避免的,因此為提高數(shù)據(jù)傳遞效率,本研究預(yù)實(shí)現(xiàn)步驟4)的簡(jiǎn)化直接計(jì)算,進(jìn)而使nC值為1 次,從總循環(huán)數(shù)將降為5.95×1010。
3 六面體網(wǎng)格分解直接計(jì)算法
數(shù)據(jù)傳遞算法步驟4)計(jì)算主要實(shí)現(xiàn)單元內(nèi)P點(diǎn)對(duì)應(yīng)的局部坐標(biāo)系值P(g,h,r)。該局部坐標(biāo)系是用于定義六面體網(wǎng)格形函數(shù)建立,如圖2 所示為局部坐標(biāo)系定義[10,14-16]。該局部坐標(biāo)系內(nèi),單元平面上局部坐標(biāo)系值分別為-1≤g,h,r≤1。計(jì)算中,只要得到實(shí)際網(wǎng)格內(nèi)任意點(diǎn)P(g,h,r)對(duì)應(yīng)的局部坐標(biāo)系點(diǎn)P(g,h,r)即可實(shí)現(xiàn)形函數(shù)方法映射。
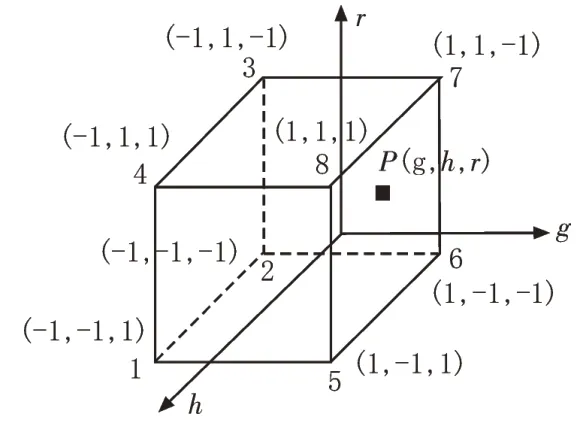
圖2 六面體單元及局部坐標(biāo)
為了避免求解式(3)非線性方程組,分解的比例系數(shù)法獲取P(g,h,r)值。首先進(jìn)行如圖3 所示的單元分解,點(diǎn)O(xO,yO,zO)為當(dāng)前單元中心點(diǎn),即為:

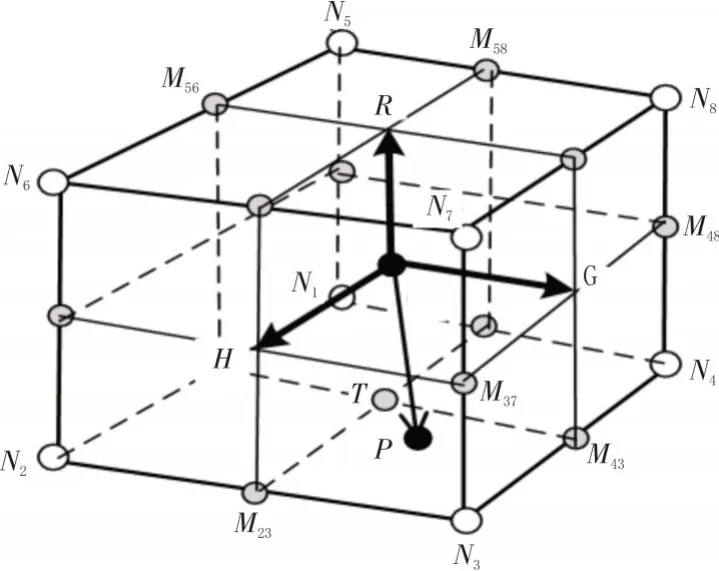
圖3 單元分解示意圖
構(gòu)建G(xg,yg,zg),H(xh,yh,zh),R(xr,yr,zr),形成確定向量3 個(gè)方向向量以及面GOH,面HOR,面GOR,從而將單元?jiǎng)澐譃? 個(gè)子域空間。根據(jù)向量與面GOH法向量nGOR的夾角θnGOR值可以判斷P點(diǎn)位于面GOR的正方向或負(fù)方向。

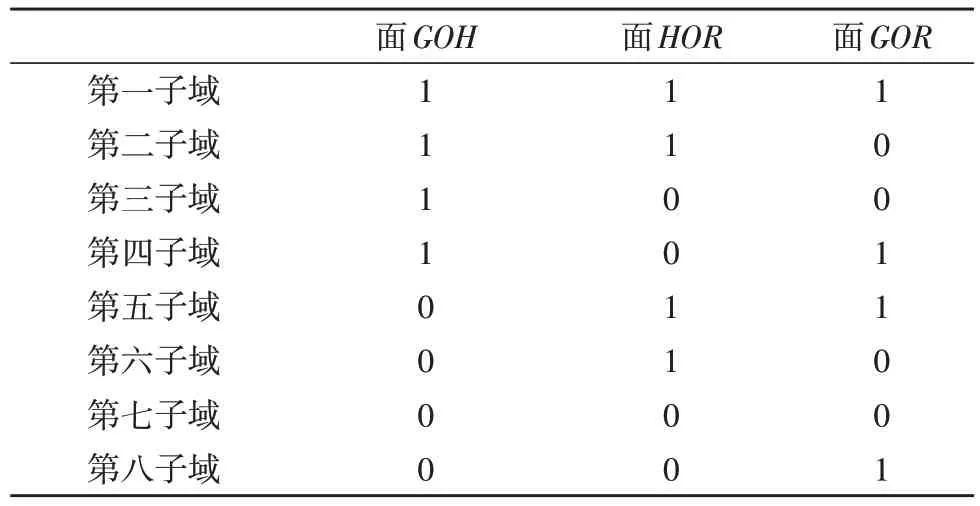
表1 P點(diǎn)子域判斷規(guī)則
根據(jù)P點(diǎn)所在子域位置,進(jìn)一步計(jì)算P(g,h,r)。按照?qǐng)D3 所示,此時(shí),P點(diǎn)位于子域六面體Esub{O,H,M37,G,T,M23,N3,M43} 內(nèi)。由于實(shí)際六面體網(wǎng)格為非理想等邊六面體,此時(shí)計(jì)算P點(diǎn)局部坐標(biāo)值(g,h,r)時(shí),g不僅僅是沿的投影,還需協(xié)調(diào)考慮相關(guān)向量。此時(shí),為了近似求解(g,h,r),該研究將的向量和平均值近似視為理想六面體的方向值,即為,如式(7)所示。

因此可以得到近似局部坐標(biāo)系值如式(8)所示。

同理可得:
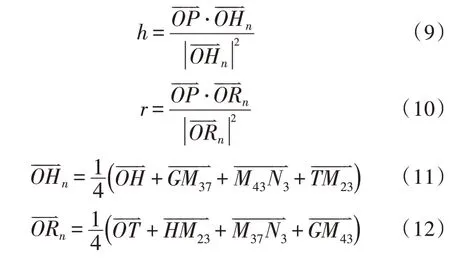
基于上述計(jì)算,即可獲得單元內(nèi)任意點(diǎn)P對(duì)應(yīng)的局部坐標(biāo)系映射值(g,h,r),實(shí)現(xiàn)了直接計(jì)算代替了迭代計(jì)算。
4 數(shù)據(jù)傳遞實(shí)例及分析
基于VC 對(duì)話框程序設(shè)計(jì)了用于網(wǎng)格數(shù)據(jù)傳遞的用戶界面,如圖4 所示。利用軟件用戶界面可以通過簡(jiǎn)單操作實(shí)現(xiàn)網(wǎng)格數(shù)據(jù)映射傳遞。具體流程如下,首先讀取所需映射計(jì)算的A 與B 網(wǎng)格數(shù)據(jù),然后讀取A 網(wǎng)格的模擬結(jié)果數(shù)據(jù),進(jìn)而在程序中建立映射所需的網(wǎng)格與模擬數(shù)據(jù)相關(guān)的數(shù)組與類信息,最后點(diǎn)擊“開始數(shù)據(jù)映射計(jì)算”按鈕實(shí)現(xiàn)數(shù)據(jù)映射計(jì)算并監(jiān)控運(yùn)算進(jìn)度。

圖4 軟件用戶界面
如圖5 和圖6 所示分別為將孔板與T 型焊接結(jié)構(gòu)的細(xì)網(wǎng)格A 模擬數(shù)據(jù)傳遞至粗網(wǎng)格B。由云圖結(jié)果可知,兩種結(jié)構(gòu)網(wǎng)格A 與網(wǎng)格B 的應(yīng)力分布基本一致,由表2 數(shù)據(jù)可知,孔板結(jié)構(gòu)差異網(wǎng)格數(shù)比為ηk=12.7,而T 型焊接件的差異網(wǎng)格數(shù)比為ηt=62.6 。由圖7 和圖8 所示的Mise 應(yīng)力曲線對(duì)比可知,對(duì)比范圍內(nèi)數(shù)據(jù)傳遞獲得粗網(wǎng)格的應(yīng)力值基本與細(xì)網(wǎng)格的值一致,僅在結(jié)構(gòu)邊緣附近,由于網(wǎng)格尺寸差距,傳遞精度稍低,而在大部分位置傳遞數(shù)據(jù)基本與源數(shù)據(jù)一致,說明該研究采用直接計(jì)算法獲取局部坐標(biāo)映射點(diǎn)(g,h,r)是有效的。

圖5 孔板結(jié)構(gòu)Mise應(yīng)力云圖

圖6 T型焊接結(jié)構(gòu)Mise應(yīng)力云圖

表2 網(wǎng)格數(shù)據(jù)傳遞信息

圖7 T型結(jié)構(gòu)背側(cè)Mise應(yīng)力隨縱向焊接路徑

圖8 孔板中心至邊緣不同距離的Mise應(yīng)力曲線
5 結(jié)論
基于對(duì)單元形函數(shù)分析,設(shè)計(jì)并開發(fā)了實(shí)現(xiàn)差異六面體網(wǎng)格間模擬數(shù)據(jù)傳遞的程序,并成功實(shí)現(xiàn)了孔板與T 型焊構(gòu)件由粗網(wǎng)格向細(xì)網(wǎng)格的模擬數(shù)據(jù)傳遞,對(duì)比數(shù)據(jù)傳遞前后結(jié)果可知,其應(yīng)力值傳遞結(jié)果數(shù)據(jù)與源結(jié)果模擬數(shù)據(jù)基本一致,且其傳遞精度與差異網(wǎng)格的網(wǎng)格數(shù)比值無關(guān)。與此同時(shí),在差異六面體網(wǎng)格數(shù)據(jù)映射計(jì)算過程中,為了避免迭代循環(huán)計(jì)算單元內(nèi)任意點(diǎn)的映射局部坐標(biāo)值,提出了單元分解直接計(jì)算代替迭代求解計(jì)算方法,從而顯著減少了網(wǎng)格數(shù)據(jù)傳遞的程序循環(huán)次數(shù),提高了差異六面體網(wǎng)格間數(shù)據(jù)傳遞技術(shù)的可用性。

