三維礦山地質建模與空間分析探討
陳 楠,譚 培
(1.四川省冶金設計研究院,四川 成都 610000;2.四川省冶勘設計集團有限公司,四川 成都 610000)
近些年來,社會科學技術獲得突飛猛進的發展,計算機等硬件與軟件設施得到進步,空間信息技術也得以綜合應用,使得人們能夠在短時間內及時獲取大量的物理信息與幾何信息,了解地球環境,為實現地球數字化發展,構建數字地球體系提供支持。礦山資源是社會經濟發展的物質基礎,礦山開采的規模和數量越來越大,如何綜合性分析礦山地質環境與資源信息,以更加生動形象的方式將其展現出來,是現代礦山地質勘探以及空間分析的發展態勢[1]。礦山區域的三維地質建模以及空間分析,均需要運用數據結構,綜合三維可視化技術、圖像處理技術以及計算機圖形模擬,將礦產區域的空間數據形象、生動且有規律地表現出來,并且大量的分析與探究圖形攜帶的信息。
1 三維礦山地質建模空間插值分析
構建三維礦山地質模型時所需要應用的數據信息主要是礦山開拓工程數據、鉆孔數據以及勘測數據等,這些數據信息在大多數情況下是具有有限性的,并且分布存在著很多不規則的現象,但是礦山地質空間的數據信息具有多變性、復雜性和連續性。想要綜合運用具有離散性和有限性的礦山地質信息得到地質形態的構造和恢復礦床形態,是構建礦山地質模型的重點和必要環節[2]。為確保信息數據的綜合性運用,利用空間插值能夠獲得良好的效果,同時還可以將空間測量的數據信息進行快速轉換,形成具有連續性的空間數據。空間插值的理論基礎是對空間位置上的點做出假設,當這些點相互靠近的時候,便更加有可能獲得相似的特征值,而當這些點相互之間的距離越遠的時候,其表現出來的相似特征也就越小。
1.1 最近距離法
最近距離法又被稱作梯森多邊形法(Thiessen Polygons),這是一種分割研究空間的方法,所以又被叫作梯森分割(Thiessen Tessellaton)。這種方法可以簡單地理解為內插空間的一種措施,任何一個未知的點所獲得的數值在平面空間位置上均可以通過與其相臨近點的數值予以替代
1.2 反距離加權法
空間內插方法中,反距離加權法也是最為常見的方法之一,這種方法在運用的時候認為未進行采樣的點受到與其相臨近點的貢獻最大,總而言之,距離與貢獻兩個參數之間形成反比關系。反距離加權法的基本思想是把差值函數F(x,y)進行定義,加權平均處理各個數據點的函數值fk,其關系表達式如下所示:
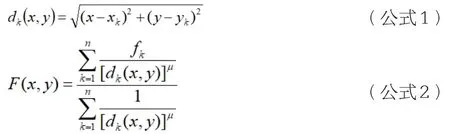
在公式1中,其所表示的含義為點(xk,yk)與點(x,y)兩點之間的距離大小,μ的取值為2。
1.3 趨勢面分析
分析趨勢面的時候,主要是以空間抽樣數據作為基礎,利用擬合的措施獲得數學曲面,通過數學曲面對空間內部的數據變化以及空間分布情況作出反映。分析趨勢面的基本思路是首先利用已經獲取的采樣點數據擬合,得到陪你規劃數學平面方程,其次在以數學平面方程組為基礎,對沒有測量值的點上的數據作出計算。趨勢面分析具有較強的適應性,第一,可以立足于空間視點對殘差與趨勢進行詮釋。第二,觀測存在限制,內插也需要以有限的數據為基礎。當殘差和趨勢可以與局部尺度和區域尺度進行聯系的時候,趨勢面分析則最具有意義。
1.4 多元回歸
從數字形式層面上分析,多元回歸類似于趨勢面,但是卻又同時存在著一定的不同。第一點,在趨勢面分析中,A所表示的是坐標矩陣,但是在多元回歸分析之中,A所表示的含義是任何變量值。第二點,在趨勢面分析中,擬合地質模型需要嚴格遵守相應的擬合規則,基本上要按照常數、一次、二次、立方的順序展開擬合,擬合過程中最為主要的是明確模型次數,所以趨勢面分析存在著很多的內在多重共線性問題。在多元回歸分析之中,即使也存在著多重共線性,但是多重共線性并非是內在的,在解決多重共線性時需要逐步回歸,由此可見,就選擇趨勢面的次數而言,多元回歸最為核心的問題是對模型作出區分以及合理化選擇變量。
1.5 樣條函數法
樣條函數是通過函數逼近曲面的一種措施,樣條函數在使用的時候具有很好的便利性,并且計算量相對較小,與空間統計法相比較而言,其特點集中在以下幾個方面。第一,不需要預先估量與計算空間方差結構。第二,可以不用進行統計假設,若表面平滑,也可以保留精度。在平滑表面狀態時,樣條函數具有合理性,需要有連續性的一階導數和二階導數。樣條函數適合于以很密的點實施內插等值線的情況。樣條函數法在應用中同樣存在著一定的不足,首先是不能夠簡單的估計出存在的誤差,其次是具有較差的點稀時效果。樣條函數具有較多的種類,在三維地質模型構建時應用最為普遍的是薄盤樣條、張力樣條以及B樣條。
1.6 克里金差值法
在地質統計學之中,克里金插值法是一種常用的空間插值法。地質統計法的出現,為空間插值提供了一種全新的優化策略,具體而言就是在進行插值時基于某種優化準則函數,對變量數值動態化的做出決定。Krige以及Matheron等人在對插值法進行研究時,將重點集中在確定權重系數領域,進而保證內插函數始終保持最佳狀態[3]。克里金插值法有協同克里金法、普通克里金法、指示克里金法、泛克里金法等等多種類型,克里金法的不同,所需要的條件也有所差異,在進行方法選擇時可以根據實際的研究需求進行選擇。當前空間插值法有很多,不同插值法所表現出來的優勢和不足以及適用范圍也各有不同。就大多數的空間插值法而言,沒有絕對最優的方法,只有在特定條件下表現出其應用優勢的方法,所以在構建礦山地質模型時,需要以實際情況為依據,綜合探索空間環境獲得數據信息,經過反復實驗進行比較以選擇合適的空間插值法。
2 三維空間分析
三維空間分析主要是基于數字高程模型,綜合運用空間分析算法,以快速獲取在某個區域范圍之內的空間特征與區域之間存在的關系[4]。三維空間分析是GIS當中最為高級的分析功能,也是對GIS進行衡量的標準,通過三維空間分析,使用者可以快速的得到結果,并且分析空間特征信息,獲得精準的結果。當前三維空間分析在應用之中所實現的功能主要有以下幾點,第一,可以定位與查詢任意點;第二,及時獲取測量點的橫向值、坡度值以及三維坐標值;第三,可以查詢物體的體積、面積、距離以及坡度面積等等;第四,可以繪制剖面圖。在三維空間分析之中,應用ArcObjects可以為使用者提供強大功能的三維分析組件,通過這些組件,使用者能夠完成多種三維分析工作。
2.1 坡度分析
水平方向與局部地表之間形成的正切值被定義為坡度,坡度所包含的內容用斜度和坡向。斜度主要是指高度變化的最大值比率,坡度主要是指變化比率最大值的方向,分析礦產地區的地貌環境時,可以應用二階差分凸率和凹率。
2.2 計算空間距離
計算空間距離時,應用的函數關系表達式如下所示:
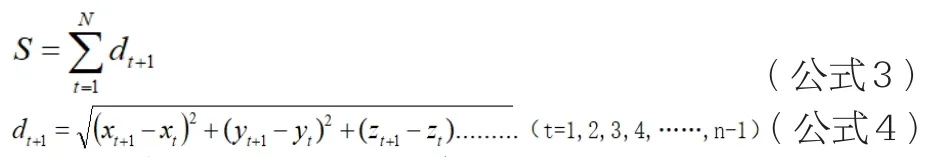
在需要勘探的地質體上任意選取兩點,通過上述公式獲取兩點之間的距離,需要注意的是,空間上的兩點主要是指在相同的巖層上的兩點。
2.3 計算多邊形面積
在構架完成的三維地質模型中,計算多邊形面積的思路是以二維環境為基礎,綜合積分原理中的梯形面積計算法。倘若是多邊形為凹多邊形,那么在進行計算的時候需要剖分多邊形,使其成為多個凸變形進行面積疊加,亦或者是三角剖分凹多邊形,之后再計算出三角形面積,完成疊加。其關系表達式如下所示:
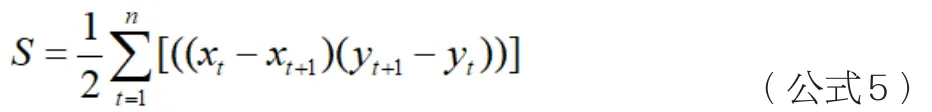
2.4 繪制剖面圖
地質勘探人員在了解地質結構時,最為常見的手段是繪制地質剖面圖,為了能夠盡可能多的從三維地質模型之中獲取相應的剖面信息,進行切割時可以選擇使用任意剖面進行模型分析。若是利用無限延展的平面對三棱柱體進行切割,那么將會得到多種切割方式。不考慮對稱性,那么將會得到35種切割方法。若是考慮對稱性以及相切情況,那么將會得到36種切割方法。
3 結束語
構建礦山三維地質模型以及進行空間分析是一項非常復雜的工程,近些年來,國內和國外的研究人員針對于三維地質模型構建以及空間分析展開了各種方式的研究。本文將以此為依據,系統性的概述當前三維礦山地質模型構建以及空間分析的方法,旨在為資源開采以及礦區地質環境監測提供借鑒。

