基于應(yīng)用案例和幾何意義的線性代數(shù)教學(xué)研究

王曉民 蘇道畢力格

摘? 要：文章討論了在線性代數(shù)教學(xué)中引入實(shí)際應(yīng)用案例和幾何意義的重要性。在線性代數(shù)教學(xué)環(huán)節(jié)中給出應(yīng)用案例和幾何意義，有助于對(duì)抽象概念加深理解，提高學(xué)生分析問(wèn)題和解決問(wèn)題的能力。通過(guò)幾個(gè)具體的應(yīng)用案例解釋了矩陣的數(shù)乘運(yùn)算、矩陣乘法、逆矩陣、特征值和特征向量，并且給出了向量組線性相關(guān)性和線性方程解的幾何意義的例子。

關(guān)鍵詞：線性代數(shù);應(yīng)用案例;幾何意義

中圖分類號(hào)：G642? ? ? ? 文獻(xiàn)標(biāo)志碼：A? ? ? ? ?文章編號(hào)：2096-000X（2021）14-0104-04

Abstract： This paper discusses the importance of introducing practical application cases and geometric meaning in the teaching of linear algebra， which is helpful to deepen the understanding of abstract concepts and improve students' ability to analyze and solve problems. Through several concrete application cases， we explained the numerical multiplication operation of matrix， matrix multiplication， inverse matrix， eigenvalue and eigenvector of matrix， and we gave some examples of the geometric meaning to the linear dependence of vector group and the solutions of linear equations.

Keywords： linear algebra; application case; geometric significance

在科技迅速發(fā)展的今天，數(shù)學(xué)的作用仍然是無(wú)法替代的，幾乎所有的科學(xué)理論最終解決都?xì)w結(jié)為數(shù)學(xué)問(wèn)題。線性代數(shù)作為數(shù)學(xué)的一個(gè)分支，在物理、化學(xué)、生物、國(guó)民經(jīng)濟(jì)、航天、航海和工程技術(shù)等領(lǐng)域都有廣泛的應(yīng)用。而且在實(shí)際問(wèn)題中，很多非線性的方程與函數(shù)問(wèn)題都可將其化成線性方程和函數(shù)進(jìn)行研究，可見(jiàn)線性代數(shù)承擔(dān)著所有的方程和函數(shù)的研究任務(wù)。特別是在工程計(jì)算中，約90%的工作量是計(jì)算線性問(wèn)題，其中約80%的計(jì)算量求解線性方程組，約10%的計(jì)算量是求解特征值和特征向量[1]，線性代數(shù)的應(yīng)用幾乎涵蓋所有的工程技術(shù)領(lǐng)域。所以在工科院校的高等教育中線性代數(shù)是必修的一門重要基礎(chǔ)課程。

一、線性代數(shù)教學(xué)現(xiàn)狀

線性代數(shù)相對(duì)其他數(shù)學(xué)分支來(lái)說(shuō)是比較簡(jiǎn)單的一門課程。但是，還有很多學(xué)生感覺(jué)線性代數(shù)難學(xué)難懂。線性代數(shù)目前主要存在的教學(xué)現(xiàn)狀有：

首先，學(xué)生感覺(jué)線性代數(shù)抽象、知識(shí)點(diǎn)多，很多概念和性質(zhì)容易混淆，不容易掌握。而且教學(xué)內(nèi)容涉及的具體實(shí)際應(yīng)用較少，教材中缺少相關(guān)生活中實(shí)際應(yīng)用性的案例。很多學(xué)生不知道線性代數(shù)會(huì)在什么地方使用，也就不知道學(xué)習(xí)線性代數(shù)的重要性，所以只能被動(dòng)地接受知識(shí)，學(xué)習(xí)過(guò)程中缺乏積極主動(dòng)性。其次，線性代數(shù)學(xué)時(shí)少，要講解矩陣、行列式、線性相關(guān)性、向量空間、線性方程組、二次型、特征值和特征向量等內(nèi)容。所以大多數(shù)教師采用以理論灌輸式的方法，很少會(huì)提及問(wèn)題的實(shí)際背景和幾何意義。這種以理論為主的傳統(tǒng)教學(xué)模式，缺少對(duì)學(xué)生啟發(fā)性和創(chuàng)新性能力的培養(yǎng)，使教學(xué)效果受到較大的影響。另外，目前使用的教材普遍內(nèi)容不夠豐富、新穎，缺少與生產(chǎn)生活實(shí)際緊密結(jié)合的具體應(yīng)用性實(shí)例，缺少幾何直觀的解釋，致使學(xué)生學(xué)習(xí)的積極性不高[2]。

二、教學(xué)環(huán)節(jié)中采取的措施

為了使學(xué)生較好地理解抽象的概念，我們可以從實(shí)際問(wèn)題出發(fā)，首先引導(dǎo)學(xué)生如何建立數(shù)學(xué)模型來(lái)分析問(wèn)題并解決這些問(wèn)題，在解決問(wèn)題的過(guò)程中再把抽象的概念和方法引出來(lái)，這樣可以達(dá)到較好的教學(xué)效果。為此我們可以采用以下措施：

（一）在教學(xué)環(huán)節(jié)中，適當(dāng)引入實(shí)際應(yīng)用案例的啟發(fā)式教學(xué)

在教學(xué)過(guò)程中，如果一個(gè)問(wèn)題沒(méi)有實(shí)際應(yīng)用的背景，那么對(duì)于線性代數(shù)知識(shí)的理解就變得很困難。如果我們恰當(dāng)適度地引入實(shí)際案例可以提高學(xué)生的學(xué)習(xí)積極性和主動(dòng)性，也可以培養(yǎng)學(xué)生把實(shí)際應(yīng)用問(wèn)題轉(zhuǎn)化成數(shù)學(xué)問(wèn)題進(jìn)行解決的能力。這樣的措施不僅有助于學(xué)生對(duì)抽象概念的理解，更能夠激發(fā)學(xué)生分析問(wèn)題和解決問(wèn)題的積極性，從而獲得較好的學(xué)習(xí)效果。例如，在向量的數(shù)乘運(yùn)算和矩陣乘法的教學(xué)中，可以引入下面經(jīng)濟(jì)學(xué)中的實(shí)際案例。

例1. 某企業(yè)生產(chǎn)一種產(chǎn)品，生產(chǎn)每單位產(chǎn)品r，需要花費(fèi)6.5元的材料、3.5元的勞動(dòng)力和1.5元的管理費(fèi)。每單位產(chǎn)品r的成本為r=（6.5，3.5，1.5）T，則100r表示的經(jīng)濟(jì)意義是什么？

解：100r表示的經(jīng)濟(jì)意義是生產(chǎn)100個(gè)產(chǎn)品r所需要的各種成本是

100r=（650，350，150）T，

這就是向量的數(shù)乘運(yùn)算。

如果直接講解向量的數(shù)乘運(yùn)算，很多學(xué)生會(huì)出現(xiàn)一部分元素乘以數(shù)k，一部分元素沒(méi)有乘以數(shù)k的情況。如果通過(guò)上面的實(shí)例講解，學(xué)生就會(huì)明白所有成本都要變成100倍，每個(gè)元素都要乘以這個(gè)數(shù)k，這樣就會(huì)避免上述錯(cuò)誤的發(fā)生。

例2. A、B兩家超市兩周的水果進(jìn)貨量和價(jià)格情況如表1、表2所示，求兩家超市第一周和第二周所進(jìn)水果的成本費(fèi)。

解：兩張表格可以寫(xiě)成以下矩陣形式，并且我們用矩陣的乘法來(lái)計(jì)算

所以A超市第一周和第二周所進(jìn)水果的成本費(fèi)分別為a11b11+a12b21+a13b31元和a11b12+a12b22+a13b32元;B超市第一周和第二周所進(jìn)水果的成本費(fèi)分別為a21b11+a22b21+a23b31元和a21b12+a22b22+a23b32元。

通過(guò)引入這個(gè)實(shí)際生活案例，學(xué)生就能非常容易掌握兩個(gè)矩陣如何相乘和矩陣乘法的實(shí)際意義。進(jìn)而學(xué)生也能夠理解兩個(gè)矩陣相乘需要滿足的條件。在教學(xué)過(guò)程中我們也可以引入剛體運(yùn)動(dòng)來(lái)解釋矩陣乘法的意義。

我們?cè)谥v解逆矩陣時(shí)，可以引入逆矩陣在加密通信領(lǐng)域中的應(yīng)用。我們可以建立一個(gè)通信加密模型。發(fā)送人：明文矩陣B——加密矩陣A——密文矩陣C。接收方：密文矩陣C——解密矩陣A-1——明文矩陣B。首先設(shè)定一個(gè)雙方都知道的加密矩陣A，使得|A|=1或-1，發(fā)送方產(chǎn)生密文矩陣C，即C=AB，因A可逆，所以接收方用解密矩陣可以得到明文矩陣B，即B=A-1C。

另外，在講解特征值和特征向量問(wèn)題時(shí)，我們可以引入人的面部圖像識(shí)別的實(shí)際應(yīng)用案例。尤其在科學(xué)技術(shù)迅速發(fā)展的今天，面部圖像識(shí)別應(yīng)用非常廣泛，是一種非常理想的身份驗(yàn)證方式。面部圖像識(shí)別實(shí)際上包含很多類問(wèn)題，例如信息壓縮和檢索、信息挖掘、圖像重建和識(shí)別等等，我們可以只介紹信息壓縮問(wèn)題。計(jì)算機(jī)上的一幅人臉圖像實(shí)際上是一個(gè)矩陣。我們的一幅1024×768清晰度的圖像，就是m=1024，n=768的m×n型矩陣。考慮簡(jiǎn)單的黑白圖像，則矩陣記錄的就是該點(diǎn)的灰度值。將每一個(gè)人的臉部圖像都標(biāo)準(zhǔn)化，這樣每一幅圖像表達(dá)為一個(gè)向量。首先在人臉的圖像庫(kù)中挑選若干“有代表性的圖像”，將其平均，得到一張“平均臉”，再把“有代表性的圖像”的相關(guān)性用矩陣A表示出來(lái)。再考慮矩陣A的特征值問(wèn)題，相對(duì)大的特征值所對(duì)應(yīng)的特征向量，對(duì)表達(dá)“有代表性”圖像集合所攜帶的信息更加重要。最大的特征值對(duì)應(yīng)的特征向量是更加宏觀的信息，某一個(gè)特征值對(duì)應(yīng)的特征向量是更加細(xì)節(jié)的信息。我們?nèi)【仃嘇的最大的n個(gè)特征值所對(duì)應(yīng)的特征向量作為人臉圖像所在的空間的基底，這樣任意一幅人臉圖像就可以用該基底近似表達(dá)出來(lái)，進(jìn)而給定的人臉圖像就可以成功壓縮存儲(chǔ)起來(lái)[5]。

除此之外，也可用Google搜索引擎來(lái)說(shuō)明特征值的應(yīng)用[5]。引入向量組的線性相關(guān)性在配制藥方問(wèn)題中的應(yīng)用等等。

（二）在教學(xué)中引入直觀的幾何教學(xué)方法，將較為抽象的內(nèi)容與數(shù)形相互結(jié)合，這樣可以把抽象的數(shù)學(xué)內(nèi)容轉(zhuǎn)換為容易理解的直觀幾何問(wèn)題

線性代數(shù)研究的是n維空間，盡管它處理的工具是代數(shù)工具，但處理的是幾何對(duì)象，例如向量空間及其變換。可見(jiàn)線性代數(shù)是代數(shù)與幾何密不可分的統(tǒng)一體。笛卡爾說(shuō)：“沒(méi)有什么東西比幾何圖形更容易引入腦際了，因此用這種方法來(lái)表達(dá)事物是非常有意義的。”希爾伯特說(shuō)：“算術(shù)符號(hào)是文字化的圖形，而幾何圖形則是圖像化的公式;沒(méi)有一個(gè)數(shù)學(xué)家能缺少這些圖像化的公式。”所以在教學(xué)中引入容易理解的直觀幾何問(wèn)題，將代數(shù)和幾何相結(jié)合，賦予抽象概念的幾何意義，有助于學(xué)生深刻理解線性代數(shù)中的一些抽象概念、定理和方法，有助于提高學(xué)生分析問(wèn)題和解決問(wèn)題的能力。例如，對(duì)于兩個(gè)向量線性相關(guān)和線性無(wú)關(guān)的定義，學(xué)生很難理解，我們可以通過(guò)幾何意義來(lái)解釋。兩個(gè)向量線性相關(guān)的幾何意義是當(dāng)且僅當(dāng)它們落在通過(guò)原點(diǎn)的同一條直線上，否則就是線性無(wú)關(guān)[3-4]。三個(gè)向量線性相關(guān)的幾何意義是這三個(gè)向量共面[1]。對(duì)于特征值和特征向量的幾何意義可以解釋為：一個(gè)圖形在空間上先沿著其矩陣的特征向量的方向旋轉(zhuǎn)，再沿著其特征向量的方向縮放特征值的大小的比例。

例3. R2的向量α=（2，1）T的幾何表示是一條由原點(diǎn)（0，0）指向點(diǎn)（2，1）的有向線段。向量β=（4，2）T與向量α線性相關(guān)，向量γ=（3，1）T與向量α線性無(wú)關(guān)。見(jiàn)圖1、圖2。

R3的三個(gè)向量α=（0，2，-1）T，β=（2，0，-1）T，γ=（1，1，-1）T線性相關(guān)，所以共面。三個(gè)向量α=（0，2，-1）T，β=（2，0，2）T，γ=（1，1，-1）T線性無(wú)關(guān)，所以非共面。見(jiàn)圖3、圖4。

例4.問(wèn)k取何值時(shí)，非齊次線性方程組

x+y+kz=4-x+ky+z=k2x-y+2z=-4，

（1）有唯一解;（2）有無(wú)窮多個(gè)解;（3）無(wú)解？

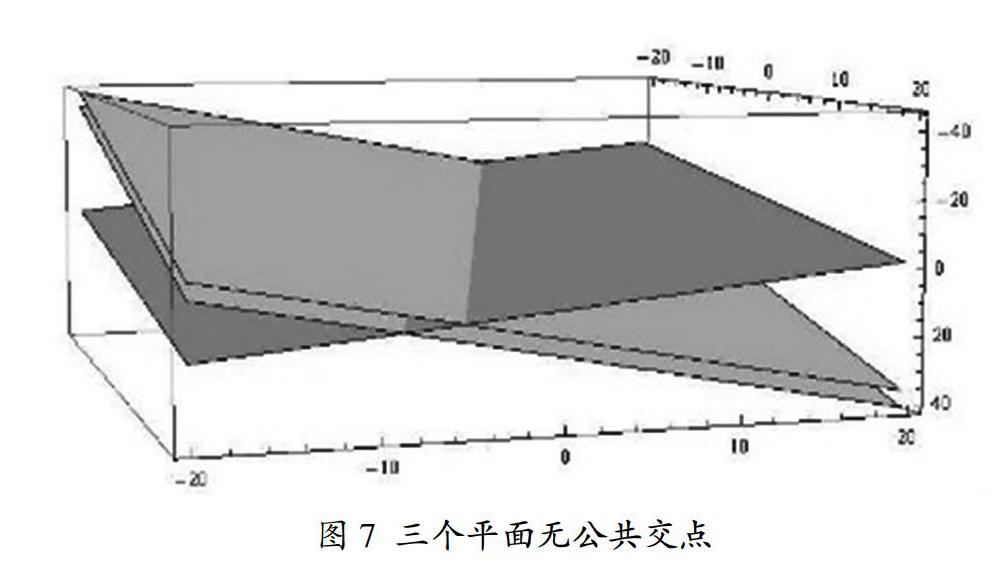
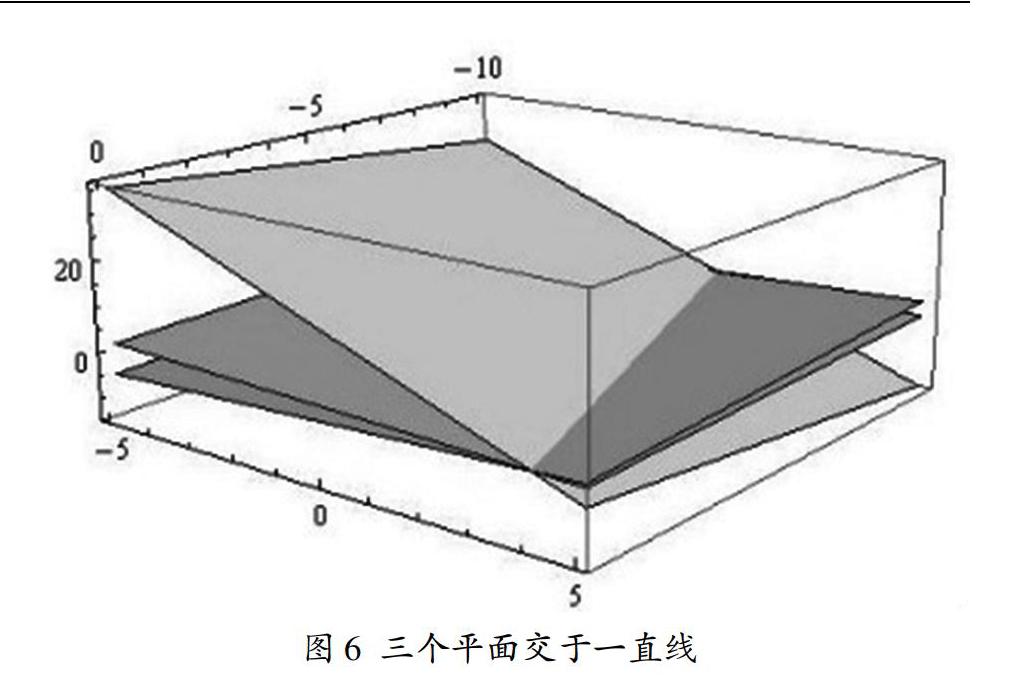
解：上述三種情況分別對(duì)應(yīng)三個(gè)平面交于一點(diǎn)、交于一直線、無(wú)公共交點(diǎn)的情形。容易算出（1）k≠-1且k≠4;（2）k=4;（3）k=-1時(shí)得到結(jié)果。見(jiàn)圖5、圖6、圖7。

另外，我們?cè)诶斫庑辛惺礁拍顣r(shí)可以采用數(shù)形結(jié)合的方式，二階行列式對(duì)應(yīng)有向面積，三階行列式對(duì)應(yīng)有向體積。線性方程組解的結(jié)構(gòu)定理對(duì)應(yīng)三維空間子空間的正交補(bǔ)，施密特正交化方法可以對(duì)應(yīng)三維空間的向量垂直問(wèn)題等等。

四、研究意義

引入應(yīng)用案例和幾何意義的啟發(fā)式教學(xué)，可以從實(shí)際問(wèn)題出發(fā)，結(jié)合相應(yīng)的直觀幾何來(lái)啟發(fā)學(xué)生的思維，充分調(diào)動(dòng)學(xué)生分析問(wèn)題和解決問(wèn)題的主動(dòng)性和積極性。

1. 如果我們通過(guò)實(shí)際案例再引出理論，使學(xué)生不再對(duì)數(shù)學(xué)理論知識(shí)感到厭煩，可以激發(fā)學(xué)生主動(dòng)獨(dú)立思考和自主學(xué)習(xí)的興趣，也提高了學(xué)生理論聯(lián)系實(shí)際的能力。

2. 恰當(dāng)適度地引入直觀幾何來(lái)解釋抽象的概念是非常重要的。引入直觀幾何，利用圖形相結(jié)合的教學(xué)方式關(guān)鍵在于能有效啟發(fā)學(xué)生的思維，彌補(bǔ)學(xué)生在應(yīng)試模式下，從小就失去的興趣和個(gè)性的發(fā)展。同時(shí)也避免了沒(méi)有教師的一系列指導(dǎo)，學(xué)生雖然掌握了足夠的知識(shí)也無(wú)法進(jìn)行自主學(xué)習(xí)的現(xiàn)象，這也是傳統(tǒng)的填鴨式教學(xué)給學(xué)生帶來(lái)的危害，使學(xué)生失去了自己的個(gè)性，缺乏對(duì)自己興趣的探索。

我們應(yīng)該積極探索更有效的啟發(fā)式教學(xué)，給學(xué)生留出足夠的時(shí)間去獨(dú)立思考，自主學(xué)習(xí)，避免每個(gè)學(xué)生所掌握的知識(shí)都來(lái)自于教師盲目的填鴨式輸入。避免教師把每一個(gè)知識(shí)點(diǎn)都徹底地分解，要給學(xué)生保留一部分，讓他們自己去分析問(wèn)題然后再解決問(wèn)題，這樣才能充分發(fā)揮自己的想象力和創(chuàng)造力，使自己的大學(xué)生活更加豐富多彩，以至于在未來(lái)的職業(yè)生涯中能更多一份自信和坦然。

參考文獻(xiàn)：

[1]烏力吉，楊海東.線性代數(shù)[M].北京：高等教育出版社，2012.

[2]金英花，江正仙，崔金超.基于應(yīng)用的線性代數(shù)教學(xué)研究與探索[J].教育教學(xué)論壇，2018（26）：178-179.

[3]戴維C雷.線性代數(shù)及其應(yīng)用（第四版）[M].劉深泉，張萬(wàn)芹，等譯.北京：機(jī)械工業(yè)出版社，2017.

[4]任廣千，謝聰，胡翠芳.線性代數(shù)的幾何意義[M].西安：西安電子科技大學(xué)出版社，2015.

[5]白峰杉.數(shù)值計(jì)算引論（第二版）[M].北京：高等教育出版社，2010.