基于改進SWT模型的FGH96合金低周疲勞壽命預測
肖陽,秦海勤,徐可君,賈明明,張柱柱
海軍航空大學 青島校區,青島 266041
作為航空發動機關鍵熱端部件,高壓渦輪盤長期處于高溫、高壓、高轉速等嚴酷環境下,承受著離心載荷、熱載荷、振動載荷等多種載荷循環往復的交互作用[1]。尤其對于艦載機發動機而言,其使用環境與陸基飛機具有較大差異,即由于跑道長度有限,起飛過程中需要發動機能夠提供足夠大的推力來滿足起飛要求,降落時發動機仍要保持較高的轉速和良好的加速性以滿足復飛,從而使得艦載機發動機高壓渦輪盤的使用條件更加惡劣,同時也對高溫下渦輪盤材料的強韌性、耐久性及抗疲勞性提出了更高要求[2]。粉末高溫合金具有組織均勻、晶粒度小和無宏觀偏析等優點,其高溫下力學性能遠遠高于傳統鑄造變形高溫合金[3],被認為是目前先進航空發動機渦輪盤的首選材料[4]。研究表明,渦輪盤的損傷機制包括低周疲勞、高周疲勞、蠕變、高溫腐蝕及其相互作用等[5],其中低周疲勞斷裂失效是限制渦輪盤使用的最主要失效模式之一[6-8]。因此,為促進FGH96粉末高溫合金能夠盡快安全、可靠地應用于我國某型高推重比航空發動機渦輪盤上,有必要針對其高溫下的低周疲勞壽命預測方法開展進一步研究。
截止目前,國內外專家學者相繼提出了多種低周疲勞壽命預測模型,包括M-C(Manson-Coffin)[9]方程、Morrow彈性應力修正模型[10]、M-H(Manson-Halford)應力修正模型[11]以及SWT(Smith-Watson-Topper)模型[12]等。其中,由于M-C方程形式簡單而被廣泛應用工程實際,然而該方程是在應力比R=-1的試驗數據基礎上擬合得到的,未考慮平均應力對部件疲勞壽命的影響。但相關研究發現[13-14],平均應力的存在會降低材料的疲勞性能,為此,Morrow[10]認為平均應力只對材料的應變-壽命曲線中的彈性部分產生影響,于是對M-C方程中彈性部分進行了平均應力修正,提出了Morrow彈性應力修正模型。但該模型只對鋼制等部分材料預測精度較高,對鋁制等材料壽命預測誤差較大,因此Morrow模型存在適用范圍較小的缺陷[15]。為考慮平均應力對材料塑性變形的影響,Manson和Halford[11]對Morrow模型進行了改進,提出了M-H應力修正模型,然而該模型僅對Morrow模型的塑性部分進行了平均應力修正,而未考慮平均應力對損傷控制參數(即損傷變量,反映材料性能劣化的參量)的影響,導致其對應變-壽命曲線中的塑性部分估計過高而使得模型預測精度較低[15]。基于此,Smith等[12]將材料的低周疲勞斷裂形式分為剪切型和拉伸型兩種,對于拉伸型破壞,平均應力對疲勞壽命的影響與載荷譜的最大應力有關,在給定疲勞壽命下最大應力和應變幅會發生變化,但二者的乘積會保持不變,于是以最大應力和應變幅作為損傷控制參數提出了SWT模型。與其他模型相比,對以拉伸開裂為主要起裂模式的材料,SWT模型可以較好地描述拉伸應力和應變在低周疲勞中的作用[16],對大部分材料具有較好的壽命預測結果,但SWT模型忽略了不同材料對平均應力影響的敏感程度[17],即平均應力對不同材料疲勞壽命的影響程度,從而導致對于某些材料的低周疲勞壽命區域預測結果偏于保守。針對此,Lv等[18]基于Walker平均應力修正準則,建立了表征材料對平均應力影響靈敏度的Walker指數的計算公式,并對SWT模型損傷控制參數進行了修正,通過對GH4133等四種材料進行壽命預測,發現修正后的SWT模型具有較好的預測效果,預測結果基本落在±1.5倍分散帶附近。但本文利用該模型對高溫下FGH96粉末高溫合金的低周疲勞壽命進行預測時發現,該模型對高應力水平下的壽命預測精度較高,當應力水平較低時,會出現由于損傷控制參數對平均應力影響效應估計過低而導致預測壽命偏于保守的問題。
為此,本文利用材料的屈服強度和抗拉強度,對Lv等[18]提出的Walker指數計算公式作了進一步改進,并對SWT模型中的損傷控制參數和塑性變形參數進行了修正,從而建立了一種基于改進SWT模型的低周疲勞壽命預測方法,并將其應用于高溫下FGH96合金的低周疲勞壽命預測。同時利用不同材料的試驗數據,對改進的Walker指數計算公式和SWT模型的有效性和適用性進行了驗證。
1 改進SWT模型的建立
由于平均應力的存在會對材料的低周疲勞壽命產生顯著影響[19-20],為此,Morrow[10]及Manson和Halford[11]在M-C方程的基礎上,分別提出了考慮平均應力效應的壽命預測模型:
(1)
(2)
式中:εa為應變幅;σ′f為疲勞強度系數;ε′f為疲勞延性系數;σm為平均應力;E為彈性模量;Nf為疲勞壽命;b為疲勞強度指數;c為疲勞延性指數。
實際應用中發現上述兩種模型對平均應力的影響效應估計不準,導致模型的適用范圍具有一定的局限性[15]。為此,Smith等[12]提出了一種形式簡單且不依賴材料性能參數的平均應力修正準則(SWT平均應力修正準則):
(3)
式中:σar為等效對稱應力幅;σmax為循環應力峰值;σa為循環應力幅;R為應力比。
同時,Smith等[12]認為拉伸破壞時載荷譜的最大應力控制著平均應力對疲勞壽命的影響程度,在給定疲勞壽命下,最大應力σmax(應變控制)或最大應變幅εa(應力控制)會發生變化,但二者的乘積會保持不變,因此以σmaxεa作為損傷控制參數,提出了SWT模型[12]:
(4)
與其他模型相比,SWT模型可以較好地反映平均應力對材料壽命的影響,對大部分材料壽命具有較好的預測結果。但SWT模型只考慮了最大應力對平均應力效應的影響,未考慮不同材料對平均應力影響的敏感程度,同時忽略了平均應力對材料塑性變形的影響,導致對于某些材料的預測結果偏于保守[15]。
Walker認為不同材料對平均應力影響的靈敏度是不同的,于是引入一個材料常數γ并將其與應力比相關聯,來反映不同材料對平均應力影響的靈敏度,進而提出了Walker平均應力修正準則[21]:
(5)
式中:γ為Walker指數。
對比SWT和Walker修正準則可知,SWT準則是Walker準則的一種特殊形式,當γ為0.5時,Walker準則退化為SWT準則,即SWT準則將不同材料對平均應力影響的靈敏度當作一個常數,從而導致SWT準則對于某些材料的平均應力修正效果沒有Walker準則好[17]。
基于此,Lv利用2倍的Walker指數γ對SWT模型中的損傷控制參數進行平均應力修正,即同時考慮了最大應力和不同材料對應力比的敏感性對平均應力修正的影響,從而提出了一種基于Walker指數和SWT參數的應變壽命預測模型[18]:
(6)
由于不同材料的γ值需要通過大量的試驗數據得到,其應用范圍受到一定限制[22]。為此,Lv通過對多種材料的疲勞性能參數進行對比,發現γ的大小和材料的屈服強度以及抗拉強度存在一定的內在聯系,且當二者數值接近時,γ的值趨近于0.5,于是提出了一種Walker指數的計算公式[18]:
(7)
式中:σ0.2為屈服強度;σb為抗拉強度;+和-的選取可參考同類材料的試驗值進行判斷。
將式(7)代入式(6),得到Lv模型[18]的表達式為
(2Nf)2b+ε′fσ′f(2Nf)b+c
(8)
γ值越大,說明材料對平均應力越不敏感[22]。因此在利用Lv模型對高溫下FGH96合金低周疲勞壽命進行預測時發現,由于式(6)左端Walker指數γ乘以2倍因子后,導致損傷控制參數對平均應力影響效應修正過低,降低了材料對平均應力影響的靈敏度,從而導致應力水平較低時FGH96合金的預測壽命偏于保守。
γ值的大小與材料的屈服強度和抗拉強度有關,當二者數值接近時γ的值趨近于0.5,于是Lv以0.5為邊界條件提出了γ的計算方法。但本文認為0.5只是一種近似值,缺乏一定的說服力。因此本文以材料的屈服強度與抗拉強度比值的1/2作為邊界條件,對式(7)作了進一步改進:
(9)
由式(9)可知,當材料的屈服強度和抗拉強度比較接近時,γ的值將趨近于0.5,此時式(9)將退化為式(7),即式(7)是本文改進Walker指數計算方法的一種特殊形式。
同時為考慮平均應力對材料塑性變形的影響,參考M-H模型[11]的修正方法,將式(4)中的塑性變形參數ε′fσ′f修正為
(10)
最后將式(9)和式(10)代入式(6),得到一種新的改進SWT模型:
(11)
2 FGH96合金低周疲勞試驗
試驗材料為FGH96粉末高溫合金,是中國自主生產的第二代損傷容限型鎳基粉末高溫合金,采用等離子旋轉電極工藝制粉+熱等靜壓制備盤坯+等溫鍛造成形。熱處理制度為:1 110~1 120 ℃完全固溶2 h,600 ℃鹽淬,760 ℃下保溫16 h,爐冷至550 ℃后空冷。合金主要強化項為γ′相,體積含量約為36%左右,在晶界及晶內彌散析出,析出溫度約為1 030~1 090 ℃,通過控制γ′相含量來獲得粗晶晶粒,優化了各元素成分和制造工藝。FGH96合金主要化學成分及試樣形狀尺寸如表1、圖1所示。
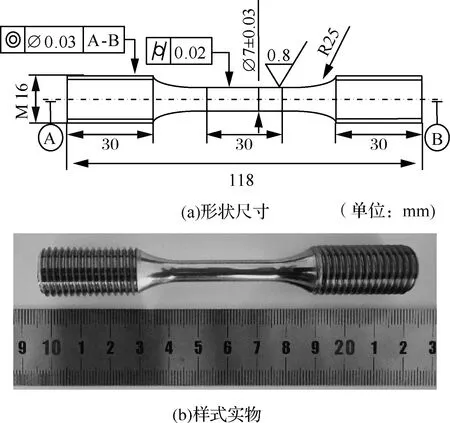
圖1 FGH96試樣

表1 FGH96合金主要化學成分(wt%)
低周疲勞試驗在PA-300型高溫疲勞試驗機上進行,通過Epsilon高溫動態引伸計(標距25 mm,量程±2.5 mm,精度0.5%)測量試樣變形。試驗過程參照GB/T 15248—2008《金屬材料軸向等幅低循環疲勞試驗方法》,試驗溫度為550 ℃,采用應力控制,應力峰值為650~1 150 MPa,試驗頻率為5 Hz,應力比R=0.06,波形為正弦波。試驗設備及斷后試樣如圖2所示,試驗結果見表2。

圖2 試驗設備及斷后試樣
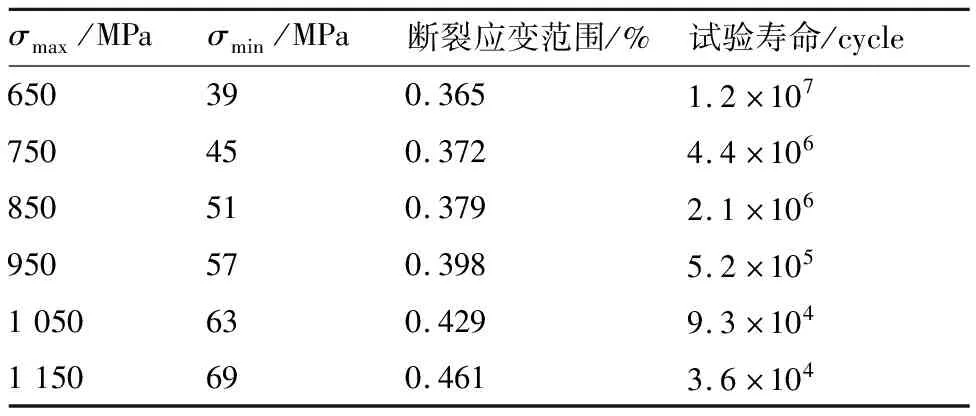
表2 FGH96合金低周疲勞試驗結果
3 模型驗證
3.1 改進Walker指數計算方法驗證
γ試驗計算值可利用不同應力比及應力水平下的低周疲勞試驗數據,代入式(6)并取平均進行計算得到。
為驗證改進Walker指數計算方法的準確性和有效性,將不同材料的屈服強度和抗拉強度代入到式(9)中,得到Walker指數的計算值γ2,然后將其與試驗計算值γ1以及根據式(7)得到的計算值γ3進行對比,計算結果如表3所示。
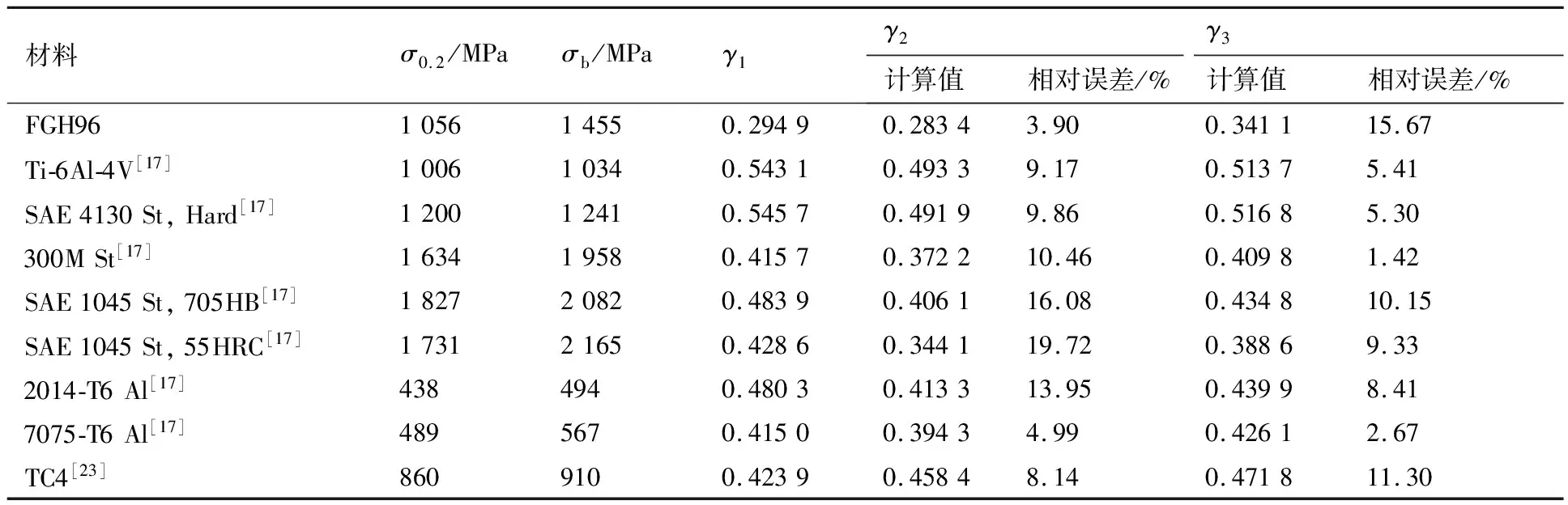
表3 γ試驗計算值與式(7)、式(9)計算值對比
由表3可知:通過式(7)和式(9)計算得到的γ值的平均相對誤差分別為7.74%和10.25%,二者相差2.51%,說明改進后的Walker指數計算方法是可行的。
3.2 改進SWT模型驗證
FGH96合金的相關材料參數如表4所示。其中,參數b和c的獲取未用到表2中的試驗結果,而是利用改進的通用斜率法[24]直接給出,即b=-0.09,c=-0.56,參數σb、σ0.2及E參數通過拉伸試驗獲得,參數σ′f、ε′f根據文獻[25]提出的方法獲得:
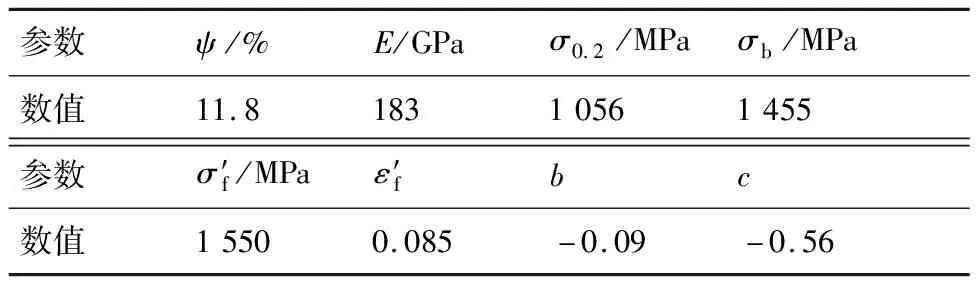
表4 550 ℃時FGH96合金材料參數
(12)
(13)
式中:ψ為斷面收縮率。
分別采用改進SWT、M-H、SWT和Lv模型,利用表2中試驗測得的應力、應變值,對不同應力水平下的FGH96合金低周疲勞壽命進行預測,計算結果如表5、圖3所示。其中,Nf1、Nf2、Nf3、Nf4分別為改進SWT、M-H、SWT和Lv模型的預測壽命。
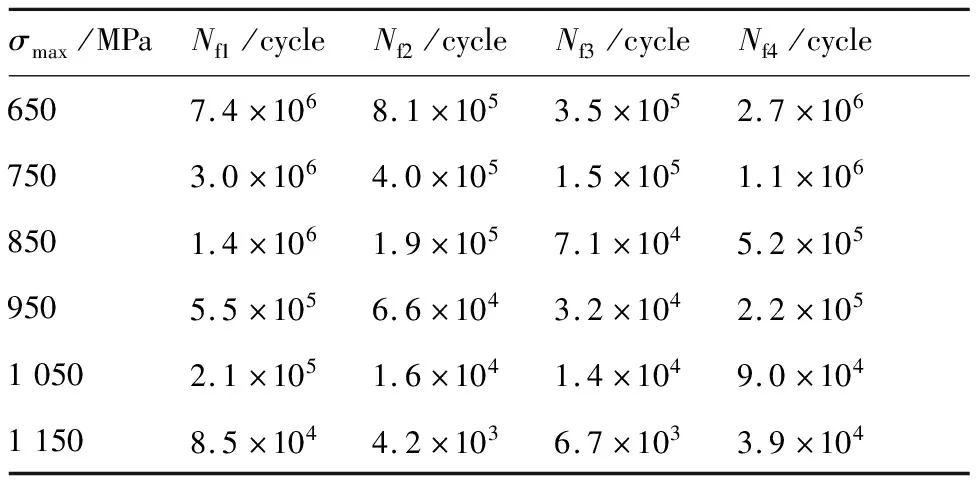
表5 FGH96合金壽命試驗值與預測值
由圖3可知:改進SWT模型對不同應力水平下的FGH96合金低周疲勞壽命預測效果較好,大部分預測結果位于±2倍分散帶之內;Lv模型對于高應力水平下的預測結果較好,預測結果基本位于±2倍分散帶之內,但當應力水平較低(650~950 MPa)時預測結果偏于保守,預測結果均位于±2倍分散帶之外。SWT模型和M-H模型對FGH96合金的預測效果較差,所有預測結果均位于±3倍分散帶之外。
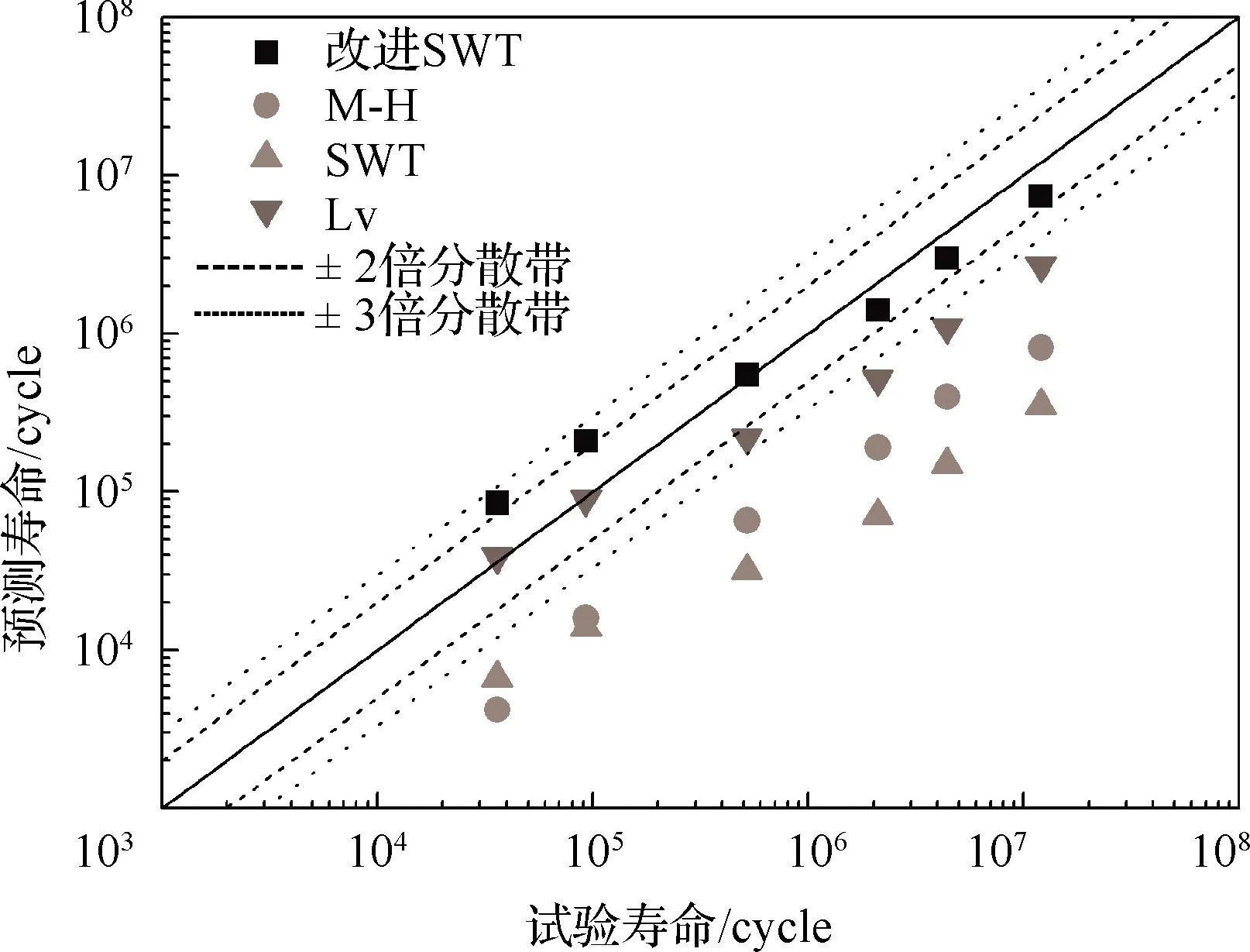
圖3 FGH96合金壽命預測分散帶
為進一步考察改進SWT模型對其他航空發動機材料的壽命預測效果,利用文獻[26]中試驗測得的TC4、GH909和TA11合金的應力、應變及疲勞壽命數據,對改進模型的預測精度和適用范圍作進一步驗證。TC4、GH909和TA11合金相關材料參數如表6所示,其中各合金材料參數b和c利用文獻[26]中的相關試驗數據擬合得到。各模型壽命預測結果如表7、圖4所示。

表6 TC4、GH909及TA11合金材料參數[26]
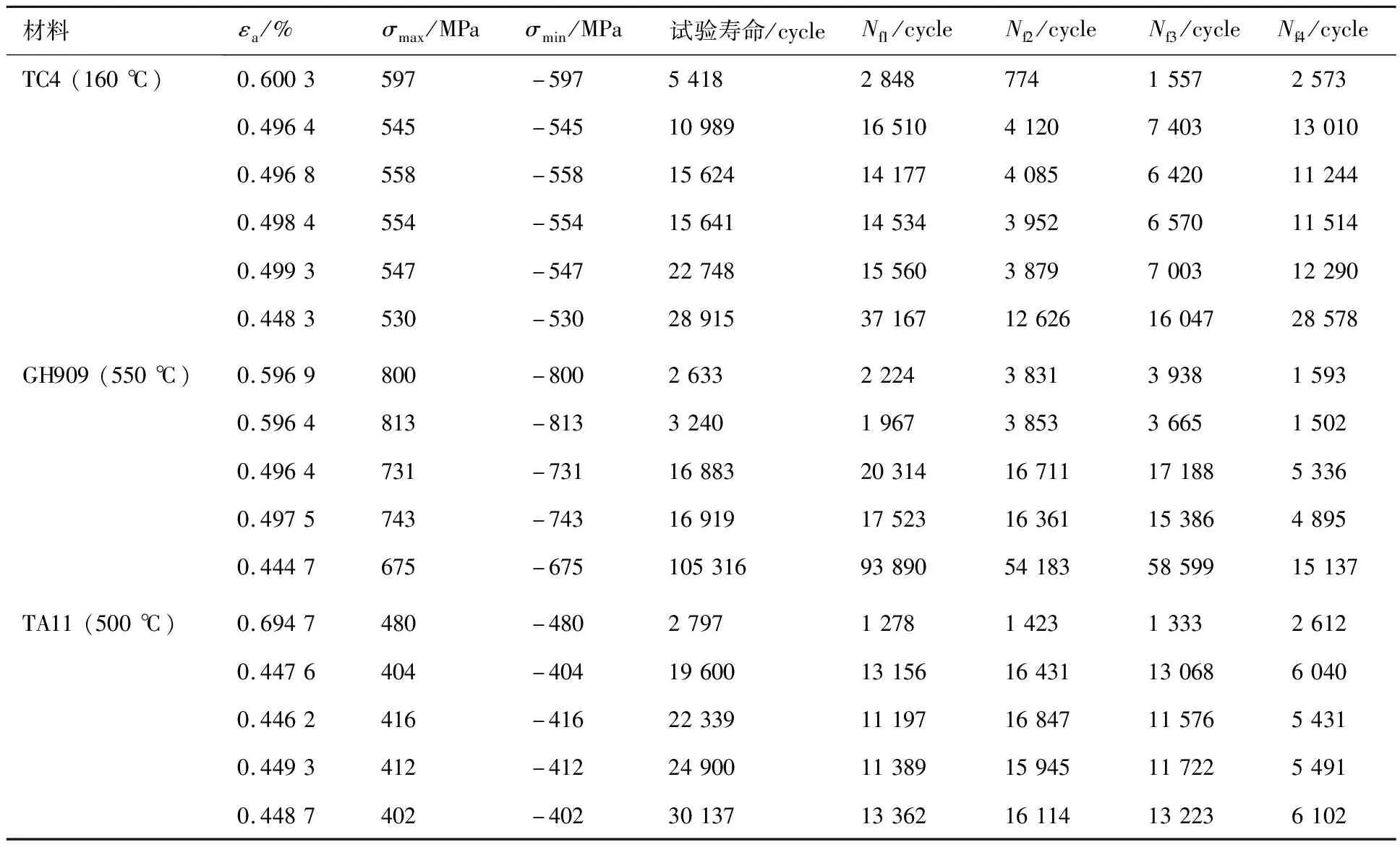
表7 TC4、GH909及TA11合金壽命試驗值[26]與預測值
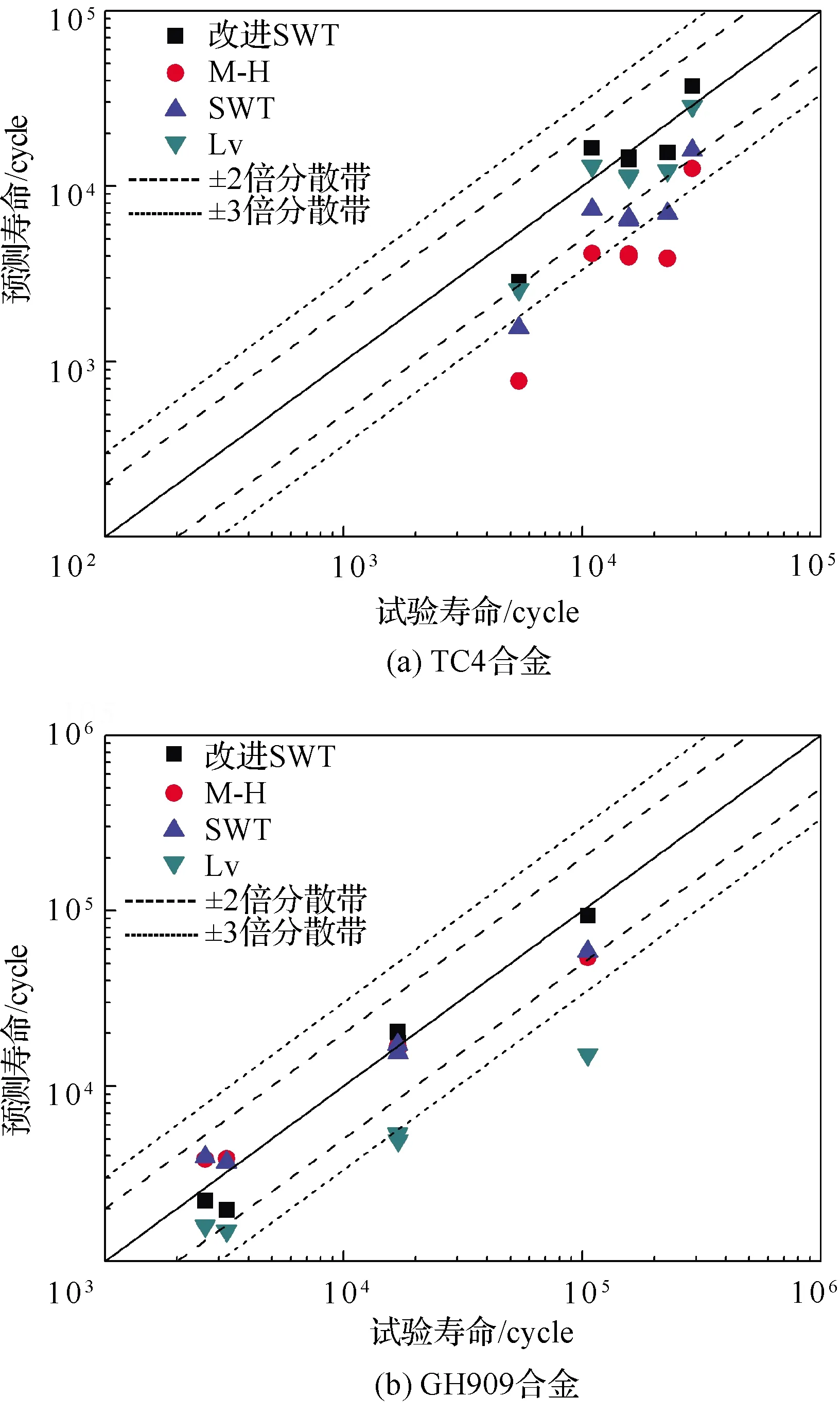
圖4 不同合金壽命預測分散帶
由圖4可知:基于改進SWT模型的TC4、GH909以及TA11合金的壽命預測結果基本上位于±2倍分散帶之內,說明新模型對不同材料具有較好的預測能力;Lv模型對TC4合金預測效果較好,但對于GH909合金和TA11合金預測誤差較大,大部分預測結果位于±2倍分散帶之外;SWT和M-H模型對GH909和TA11合金預測精度較高,預測結果基于位于±2倍分散帶之內,但對于TC4合金的預測結果偏于保守,部分預測結果位于±3倍分散帶之外。
4 結 論
1)利用材料的屈服強度和抗拉強度對Lv提出的Walker指數計算方法進行了改進,并將其引入到SWT模型中對其損傷控制參數進行了修正。同時結合M-H模型塑性部分平均應力修正的優點,對SWT模型的塑性變形參數進行了修正,進而提出了一種基于改進SWT模型的FGH96粉末高溫合金低周疲勞壽命預測方法。
2)利用不同材料的γ試驗計算值對改進的Walker指數計算方法進行了驗證,發現改進后γ的計算平均相對誤差為10.25%,與改進前僅相差2.51%,證明了改進方法的準確性和有效性。
3)分別利用FGH96合金以及TC4等航空發動機材料的低周疲勞試驗數據,對改進SWT模型進行了評估。結果顯示,改進SWT模型對不同材料具有較高的預測能力,壽命預測結果基本位于±2倍分散帶以內,而其余3種模型僅對部分材料具有較好的預測效果,從而說明改進SWT模型具有較好的預測能力和適用范圍。

