金剛石納米顆粒對齒面接觸剛度的影響研究*
朱青青 李媛媛 宋 娟 劉 娜 劉培學
(①青島黃海學院,山東 青島 266427;②中國石油大學(華東),山東 青島 266580)
齒輪系統屬于非線性振動系統,齒輪傳動過程中產生的振動和噪聲已成為影響齒輪壽命和傳動效率研究的重要因素。在齒輪傳動的摩擦與潤滑方面,可通過進一步優化齒輪的潤滑方法及理論,降低齒輪的振動和噪聲。
在納米潤滑添加劑的理論研究方面,黃興保等[1]建立了顆粒流潤滑模型,考慮了顆粒流對潤滑油黏度和密度的定量影響,進行了直齒輪的熱彈流潤滑研究。孟凡明等[2]基于動網格技術,研究了活塞環-缸套潤滑中顆粒直徑、位置因素和速度對總摩擦力和承載特性的影響。劉偉等[3]以有限長滑塊為對象,建立了多顆粒存在情況下的雷諾方程,探討了固-液兩相流體潤滑狀態下固體顆粒對油膜壓力的影響。劉焜等[4]基于非連續介質力學的離散單元法,建立了顆粒流潤滑的楔形滑塊研究模型,對顆粒介質的摩擦因數對摩擦學系統特性的影響進行了仿真研究。孟凡凈等[5]研究了在剪切平行板間顆粒流潤滑的流態和摩擦因數變化問題。在納米潤滑添加劑的實驗研究方面,徐愷等[6]基于納米顆粒的物化特性,探究了含納米ZrO2、SiC、SiO2、Al2O3添加劑的潤滑油對斜齒圓柱齒輪潤滑的振動和噪聲特性。馬士玉等[7]研究了SiO2納米顆粒作為潤滑添加劑的抗磨減摩性能。沈明武等[8]采用相對光強原理對超細金剛石粉添加劑的薄膜潤滑性能進行了研究。楊太永等[9]研究了微碳球及二氧化鈦納米顆粒作為潤滑添加劑時的摩擦學特性。吳明遠等[10]基于不同納米添加劑進行軸承的高速磨合實驗,探究納米添加劑對軸承振動及噪聲特性的影響。夏新濤等[11]通過試驗研究發現適量修飾過的TiO2納米顆粒作為潤滑脂添加劑時,可以改善軸承的振動和噪聲特性。
本文基于Hertz接觸理論,建立混合潤滑模型與微凸體接觸模型,研究不同百分含量的納米顆粒和齒輪轉速對齒面接觸剛度的影響,進一步豐富齒輪振動與潤滑的理論。
1 數學模型
1.1 微凸體模型
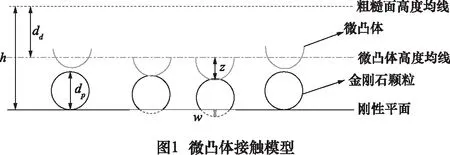
采用Greenwood-Williamson統計模型(GW模型)描述粗糙表面與剛性表面之間的接觸。關于該模型,有如下假設:(1)表面粗糙體的形狀為球狀,其曲率半徑定義為β;(2)粗糙微凸體的高度服從高斯分布,σs為其高度的標準偏差;(3)金剛石納米顆粒為球形,其直徑定義為dp;(4)剛性平面與金剛石顆粒之間的接觸為Hertz接觸;(5)金剛石納米顆粒之間的相互作用忽略不計。
根據Hertz接觸理論,金剛石顆粒與剛性平面之間的接觸力[12]為
(1)
式中:E為剛性平面與金剛石顆粒接觸的綜合彈性模量;w為彈性接觸變形。
w=z+dp+dd-h
(2)
(3)
式中:z為單個微凸體的高度,定義為微凸體高度均線與其頂點之間的距離;dp為金剛石納米顆粒的直徑,dp=300 nm;dd為粗糙面高度均線與微凸體高度均線之間的距離;h為油膜厚度;E1、E2分別為剛性平面與金剛石納米顆粒的彈性模量。
單個金剛石顆粒與剛性平面的接觸剛度為
(4)
(5)
采用GW統計學模型計算與剛性平面接觸的金剛石顆粒的個數,將單個顆粒的接觸剛度對參與接觸顆粒的個數進行積分,可得到金剛石顆粒與剛性平面接觸的總剛度。定義以下無量綱參量:
如圖1所示,當滿足以下關系時,金剛石顆粒與剛性平面接觸:
z+dp>h-dd
(6)
對應的無量綱表達式為
zn+dpn>hn-ddn
(7)
剛性平面與顆粒接觸的概率為
p(hn-ddn-dpn)=prob(zn>hn-ddn-dpn)
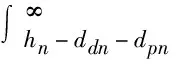
(8)
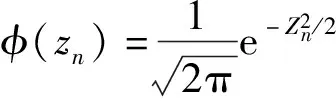
與剛性平面接觸的金剛石顆粒的總個數為
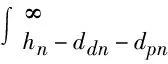
(9)
式中:N為金剛石顆粒的總個數。
顆粒接觸的總剛度為
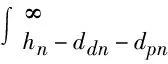
(10)
1.2 混合潤滑模型
1.2.1 Reynolds 方程
定義邊界油膜厚度hb=dd+dp,作為判斷潤滑狀態的依據。若油膜厚度大于hb,則認為該點處于彈流潤滑區,否則處于邊界潤滑區。
油膜厚度滿足h>hb時,所采用的考慮時變效應的Reynolds方程為
(11)
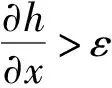
(12)
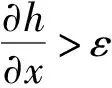
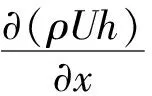
(13)
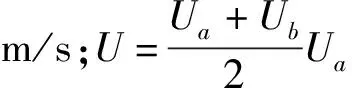
1.2.2 膜厚方程
ln(x-ζ)2dζ+δ(x,t)
(14)
式中:δ(x,t)表示粗糙表面形貌。
1.2.3 載荷方程
記w為單位長度上的載荷(N/m),則壓力應該滿足載荷方程:
(15)
式中:p=pa+ph,pa和ph分別為粗糙微凸體承載壓力與油膜壓力。
粗糙微凸體與油膜的承載比例分別為γa與γh,則
(16)
1.2.4 油膜剛度
依據載荷與中心油膜厚度計算油膜剛度[13-14]
(17)
式中:kh為油膜剛度,hc為中心油膜厚度。
1.2.5 綜合接觸剛度
定義綜合接觸剛度k,其由顆粒相接觸剛度與油膜剛度共同構成。
(18)
其他潤滑控制方程如黏壓方程、密壓方程以及各方程的無量綱化見文獻[15]。
將潤滑控制基本方程量綱一化后進行離散,編程進行潤滑求解。選取牛頓流體,采用多重網格法求解油膜壓力,采用多重網格積分法求解油膜厚度[16]。壓力的計算域為Xin=-4.6,Xout=1.4,采用W循環,利用多重網格法進行計算,劃分網格共6層,每層網格上的節點數分別為31、61、121、241、481、961,在每層網格上均進行Gauss-Seidel低松弛迭代,并把前一瞬時壓力迭代的結果作為下一瞬時進行壓力迭代的初值。迭代收斂判據為每個瞬時壓力和載荷的相對誤差小于0.001。
2 結果與討論
齒輪傳動和潤滑的基本參數見表1。
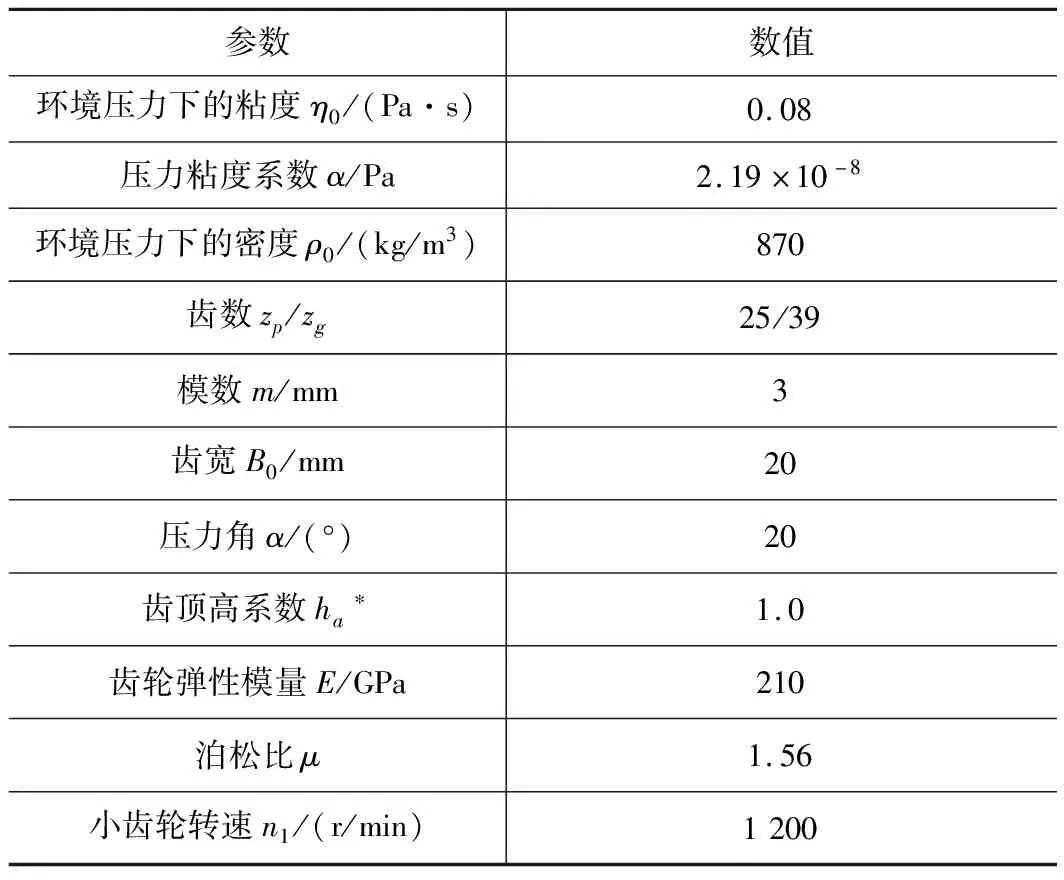
表1 齒輪傳動和潤滑的基本參數
2.1 納米百分含量對齒面接觸剛度的影響
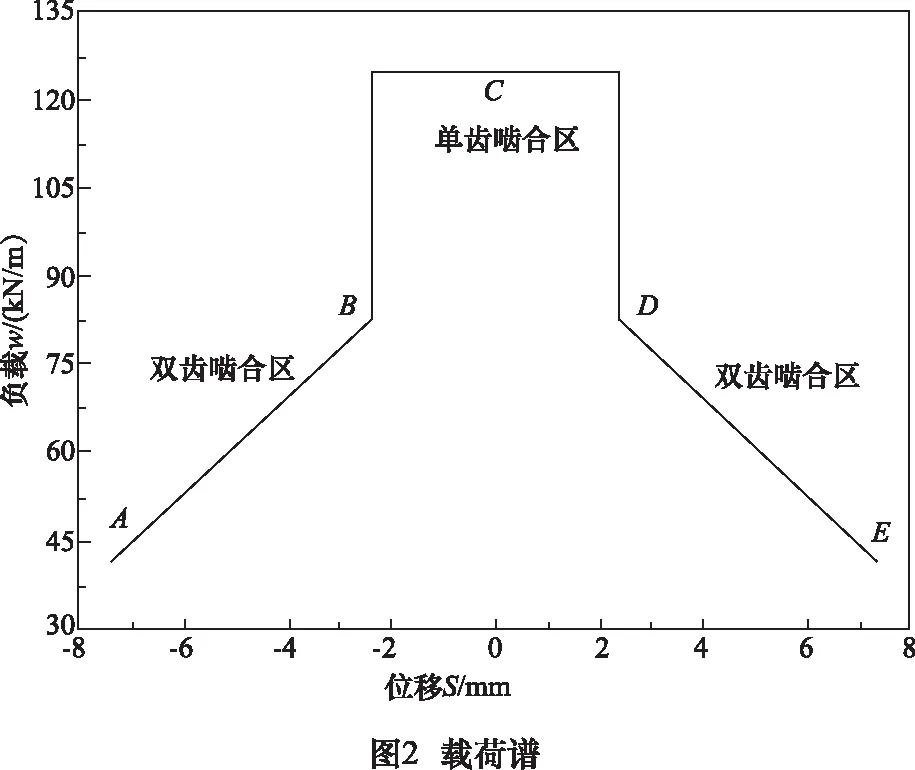
圖2所示為齒輪傳動的載荷譜。A點為嚙入點,C點為節點,E點為嚙出點,B、D點為單雙齒嚙合的臨界點。
圖3所示為金剛石百分含量不同時粗糙峰和油膜的承載比。粗糙峰和油膜承載比主要受載荷的影響。由于單齒嚙合區只有一對齒承載,單位齒寬上所承受的載荷最大,因而單齒嚙合區粗糙峰承載比例最大,油膜承載比例最小。隨著金剛石百分含量的增加,與粗糙峰和齒面接觸的金剛石顆粒數目增多,因而粗糙峰承載比例不斷增加,油膜承載比例不斷減小。
圖4為節點處的油膜壓力和油膜厚度曲線。由于粗糙峰對油膜的擠壓作用,油膜壓力出現比較明顯的峰/谷,隨著金剛石納米顆粒百分含量的增加,油膜壓力峰/谷逐漸變得平緩直至消失。其原因是:金剛石納米顆粒百分含量的增加導致粗糙峰的承載比不斷增大,油膜擠壓效應減弱;金剛石納米顆粒百分含量的增加導致納米顆粒相的增粘效應增強,油膜厚度增大且油膜壓力略有減小。
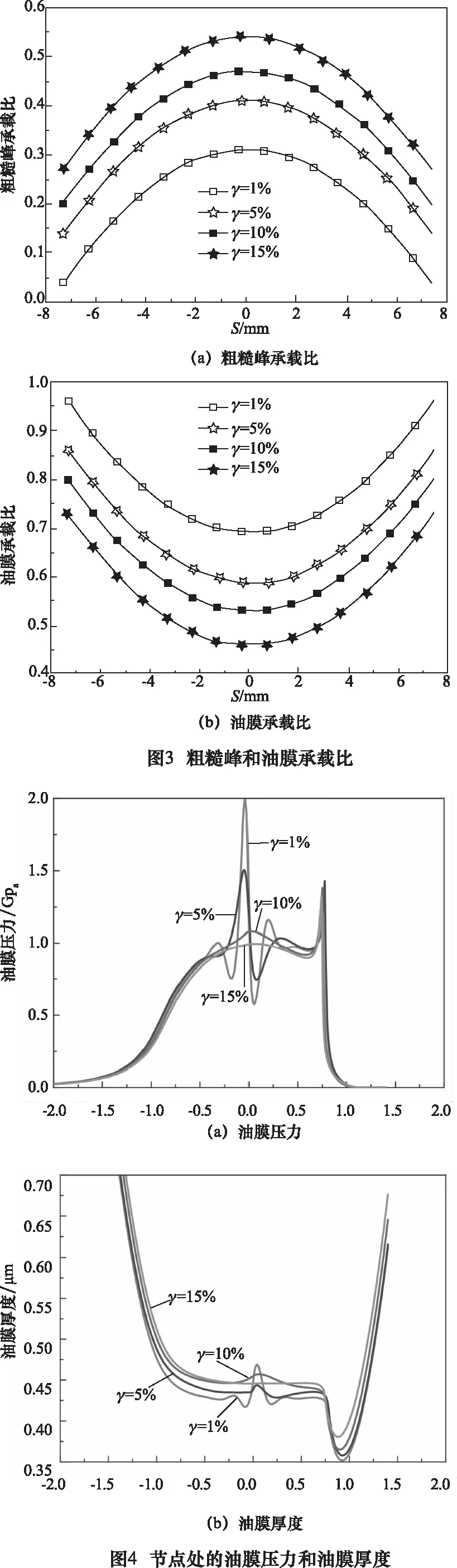
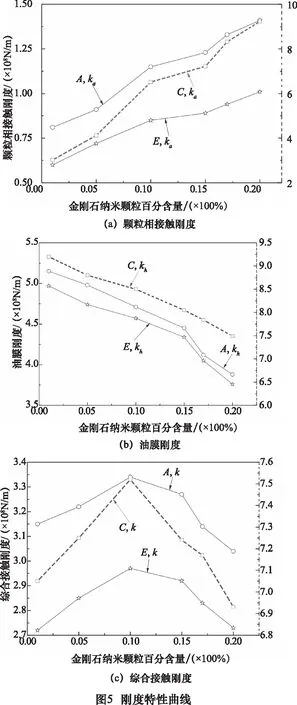
圖5a~c描述了齒輪傳動的3個特殊點處(嚙入點、節點和嚙出點)的顆粒相接觸剛度、油膜剛度和綜合接觸剛度隨金剛石納米顆粒百分含量的變化。隨著金剛石納米顆粒百分含量的增加,粗糙峰的承載比不斷增大,這導致顆粒相接觸剛度不斷增大。金剛石納米顆粒百分含量的增加導致顆粒相的增黏效應增強,這導致油膜厚度增大,因而油膜剛度呈現出不斷減小的趨勢。隨著金剛石百分含量的增加,顆粒相接觸剛度和油膜剛度呈現出兩種相反的變化趨勢,因而導致綜合接觸剛度先增大,后減小。金剛石納米顆粒的適宜百分含量為10%~15%,此時可獲得較為滿意的綜合接觸剛度,此時齒面的承載能力最強。
2.2 轉速對齒面接觸剛度的影響
圖6描述了不同轉速下粗糙峰和油膜承載比的變化。隨著轉速的增加,粗糙峰的承載比不斷減小,油膜承載比不斷增大。轉速達到1 800 r/min和2 500 r/min時,在嚙入端和嚙出端,粗糙峰承載比部分為零,載荷全部由油膜承擔,兩齒面在嚙入端和嚙出端處于彈流潤滑狀態。
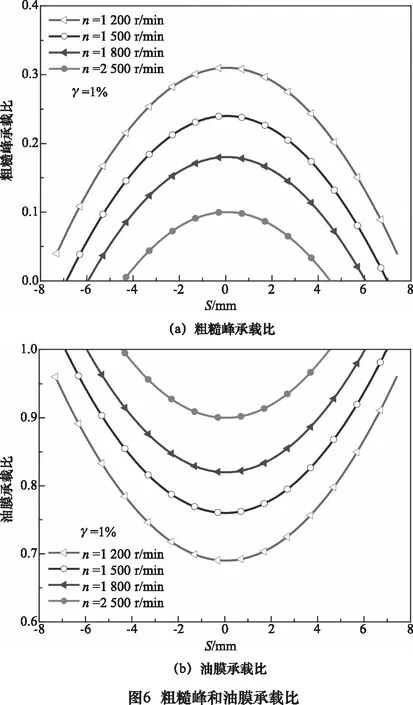
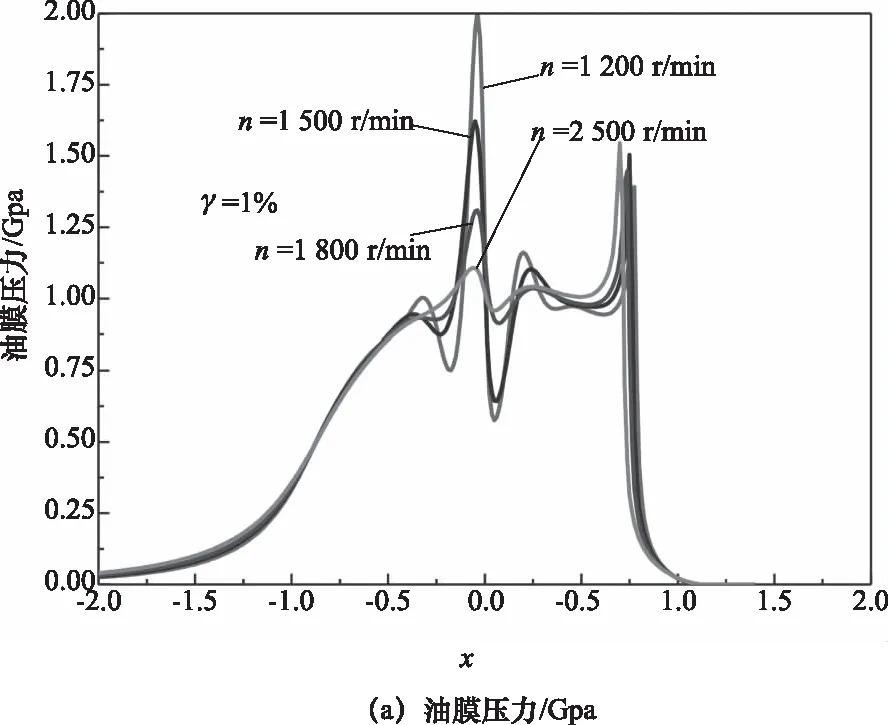
圖7為不同轉速下節點處的油膜壓力和油膜厚度曲線。隨著轉速的增加,油膜厚度增大,油膜壓力減小且其峰/谷變化趨于平緩。
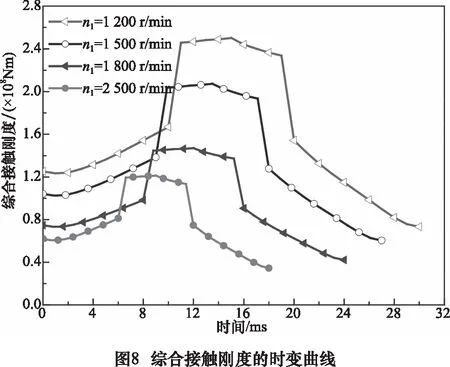
圖8為綜合接觸剛度在不同轉速下的時變曲線。轉速的增加使齒輪的嚙頻增大,嚙合周期變小。在齒輪嚙合的同一點處,綜合接觸剛度隨轉速的增加而不斷減小。金剛石納米顆粒的含量不變時,轉速的增加使油膜厚度增大,進而降低了油膜剛度,同時油膜承載比不斷增大,部分接觸點處的油膜甚至有能力將兩摩擦表面完全分隔開,這導致顆粒相接觸剛度不斷減小。顆粒相接觸剛度和油膜剛度隨著轉速的增加均不斷減小,這導致綜合接觸剛度呈現出不斷減小的趨勢。
3 結語
(1)隨著金剛石納米顆粒百分含量的不斷增加,粗糙峰承載比例和顆粒相接觸剛度不斷增加,油膜承載比例和油膜剛度不斷減小,齒面接觸剛度呈現出先增大后減小的趨勢。金剛石納米顆粒的含量為10%~15%時,可獲得較為滿意齒面接觸剛度,齒面承載能力最強。
(2)隨著轉速的不斷增加,油膜承載比雖不斷增大,但油膜剛度不斷減小,同時顆粒相承載與顆粒相接觸剛度不斷減小,導致齒面接觸剛度呈現出不斷減小的趨勢。

