白噪聲作用下欠阻尼隨機雙穩系統中的隨機共振

朱福成,郭 鋒

(1.綿陽職業技術學院,四川 綿陽 621000;2.西南科技大學信息工程學院,四川 綿陽 621000)

0 引言

隨機共振是一種出現在隨機動力系統中的非線性現象，即在弱周期力的作用下，由噪聲誘導的系統勢井間的跳躍同步行為[1]。對于隨機非線性系統而言，這種同步依賴于噪聲和周期外力間的協同作用。因此，系統非線性、驅動力的周期性、噪聲3個因素是非線性系統出現隨機共振現象的必要條件。阻尼指由于外部作用或系統內在原因而使振動系統振幅逐漸減小的物理現象。對于足夠大的阻尼力，系統處于過阻尼狀態；否則，系統處于臨界阻尼或欠阻尼狀態。對于過阻尼條件下的動力系統，其慣性項可以忽略。但是，對于中、小阻尼系統，由于慣性效應不可忽略而應建立相應的欠阻尼模型。自隨機共振現象發現以來，過阻尼非線性系統中的隨機共振受到學者們的廣泛關注。文獻[2]分析了過阻尼分數階Langevin方程產生隨機共振的內在機理。文獻[3]研究了過阻尼雙穩系統在α噪聲作用下出現隨機共振的不同特征。文獻[4]利用過阻尼Langevin方程來描述企業的隨機動力學行為，認為內外部資本環境的隨機波動產生了統計意義上的最大隨機激勵效應。文獻[5]～[7]研究發現過阻尼生物模型中也會出現隨機共振現象。文獻[8]～[10]將過阻尼雙穩系統中的隨機共振用于故障診斷和微弱信號檢測中。同時，欠阻尼動力系統中的隨機共振也得到了深入研究。文獻[11]研究了二階欠阻尼線性諧振子的穩態響應，給出了由質量及頻率漲落噪聲誘導而出現隨機共振現象的充分必要條件。文獻[12]討論了欠阻尼雙穩系統中噪聲強度、強迫頻率對系統響應的影響。文獻[13]研究表明，增加雙值噪聲非對稱參數和阻尼參數可以抑制欠阻尼系統的隨機共振現象。文獻[14]分析了泊松白噪聲作用下耦合欠阻尼雙穩態系統的隨機共振行為。文獻[15]研究發現，欠阻尼系統輸出在一二次諧波處的信噪比隨著噪聲強度的增加呈現出先最小后最大的變化規律。文獻[16]發現欠阻尼三阱勢系統存在兩個臨界阻尼值，分別會導致隨機共振的出現和消失。

上述文獻均基于系統具有確定性勢能函數的情形；在某些情況下，環境的擾動會干擾系統的勢能函數，從而勢能函數應該按隨機勢能建模。文獻[17]分析了受位置隨機擾動的過阻尼布朗粒子在周期勢中的運動，發現隨著隨機勢幅度的增加，概率流的最大值減小。文獻[18]研究發現，隨機勢對輸運過程的影響隨隨機勢振幅和隨機勢相關長度的增大而增大。文獻[19]研究發現，隨著雙穩態系統隨機勢強度的增加，信噪比存在多個峰值到沒有峰值的轉變。文獻[20]、[21]研究表明，在隨機雙穩系統的信噪比與噪聲強度、靜態力的關系曲線上出現了隨機共振現象。文獻[22]在具有波動勢壘的蛋白質—馬達系統中發現了系統的隨機共振行為。

1 隨機雙穩系統的輸出信噪比

考慮二階隨機系統(1)

(1)

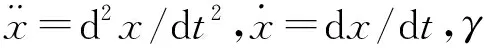
〈η(t)〉=0,〈η(t1)η(t2)〉=2Dδ(t1-t2)。

(2)

勢能函數為

(3)

其中，U0(x)為確定性勢能部分,ξ(x)為小的態變量擾動，即勢能U(x)的隨機部分,其取值為±Δ,沿一維空間隨機跳躍。ξ(x)可以用一個隨機函數n(x2,x1)表示,它表示在x=x1和x=x2坐標范圍內在+Δ和-Δ兩個數值間跳躍的次數。n(x,0)服從Poisson分布。

(4)

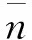
(5)

其中，L是相關長度。ξ(x)的均值和相關函數分別為

(6)

對于單一雙值勢能，有：

(7)

(8)

(9)

(10)

隨機勢ξi(x)的統計特性為

(11)

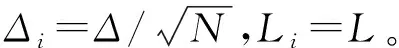
(12)

(13)

在極限N→∞下,有：

(14)

容易看出，單一雙值勢能的統計特性與Ornstein-Uhlenbeck勢能類似，本文僅考慮Ornstein-Uhlenbeck勢能。

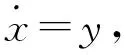
(15)

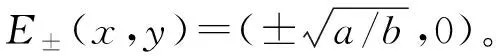
(16)

由方程(16),系統的準穩態概率密度可以表示為

(17)

(18)

設系統滿足絕熱近似條件[1],即驅動周期力的頻率Ω低于系統在某個勢井內的弛豫速率,則系統有足夠時間在一個周期T=2π/Ω的時間內達到局域平衡。由式(16),絕熱近似條件下系統在兩穩態E±間的轉移率可以表示為

(19)

W±(t)=f(α+βcos(Ωt))

(20)

可展開為

(21)

其中，

(22)

W0是系統(1)僅受噪聲作用時的Kramers速率。

(23)

(24)

對系統輸出信號的自相關函數進行傅里葉變換得到的系統輸出功率譜可以表示為

S(ω)=S1(ω)δ(ω-Ω)+S2(ω)

(25)

其中等式右端兩項分別為信號和噪聲的功率譜，系統輸出信噪比(SNR)定義為信號功率與信號頻率處噪聲功率的比值，可以表示為

(26)

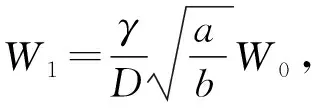
(27)

在本文后續的討論中，參數設置滿足該條件。

2 討論

當阻尼比較小時，系統為欠阻尼系統。而當隨機擾動作用在系統態變量時，系統勢能函數變成隨機函數。本文分析白噪聲作用下欠阻尼隨機雙穩系統中的隨機共振現象，基于Fokker-Planck方程,我們推導出穩態概率密度的表達式。利用兩態理論，求得系統輸出信噪比SNR的解析表達式。下面，基于式(26)來分析SNR與系統參數、噪聲參數及隨機勢能參數的依賴關系。

由圖1～圖4可見,在信噪比SNR與阻尼系數γ的關系曲線上出現了一個共振峰，即廣義的隨機共振現象。有必要指出，SNR與阻尼系數間的單峰現象是一個新的結果，在文獻[19]～[23]的欠阻尼系統中沒有研究過。同時，該非單調現象與欠阻尼線性系統中出現的現象顯然不同。對欠阻尼線性系統而言，系統輸出信號隨阻尼的增大而單調減小。該現象可以解釋為系統與噪聲間的非線性作用導致系統轉移率W±與阻尼系數有關，從而可能在某個阻尼系數時，輸出信號達到最大。由圖1容易發現，隨著系統參數a的增大,SNR向小的γ值方向移動，故對于較小的γ值,應該參數a選擇大的值以提升系統輸出信號。同時，比較圖1與圖2可見,系統參數b對SNR的影響與參數a對其影響不同。隨著參數b增大,共振峰向大的γ值方向移動,故對于大的參數b,較大的阻尼系數γ可以提升系統輸出性能。圖3表明，對于較大的噪聲強度D,相對較大的γ值可以提高系統輸出性能。隨著隨機勢幅度Δ的增大，SNR的峰值高度單調增大，如圖4所示。

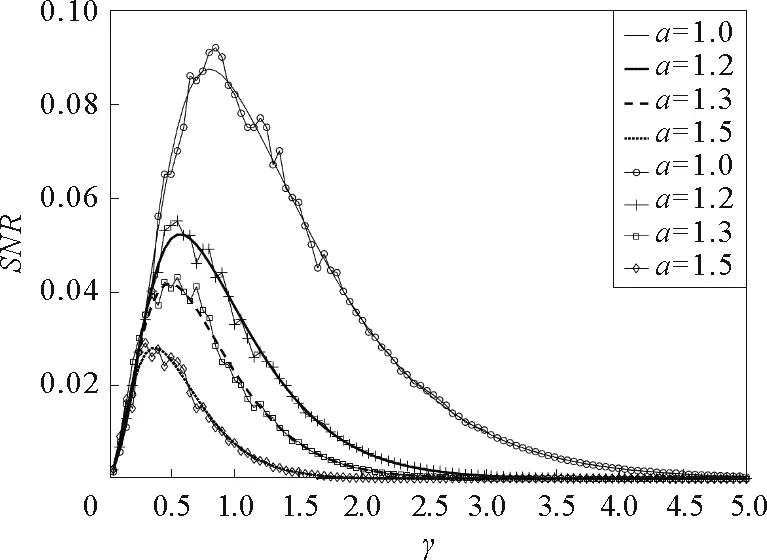
參數b=1,Δ=0.2,D=0.1,L=10,A=0.2,Ω=0.1圖1 系統參數a取不同值時信噪比SNR與阻尼系數γ的關系曲線

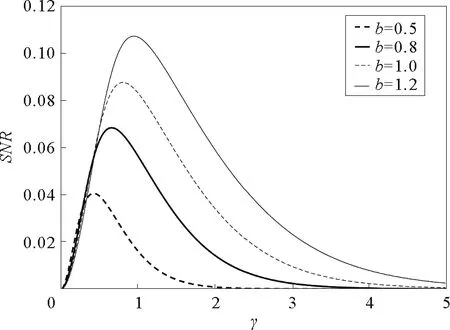
參數a=1,Δ=0.2,D=0.1,L=10,A=0.2,Ω=0.1圖2 系統參數b取不同值時信噪比SNR與阻尼系數γ的關系曲線

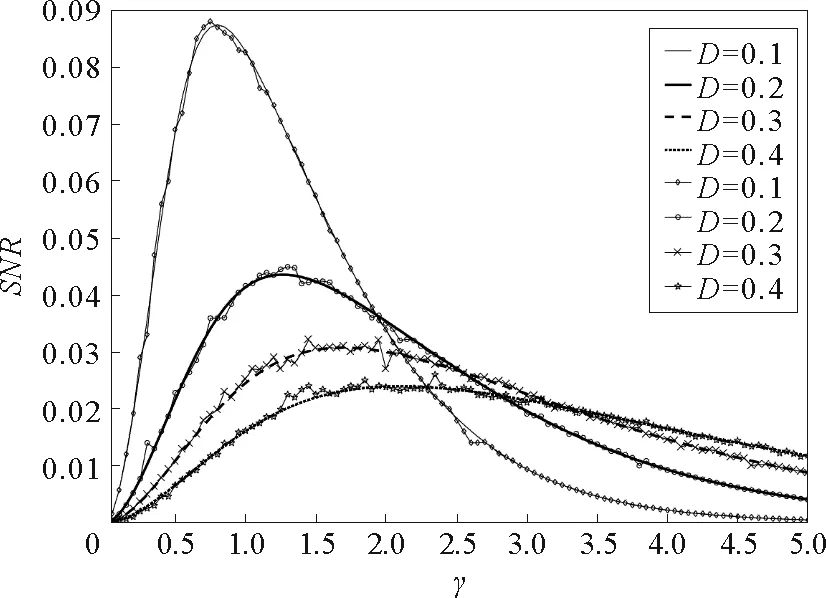
參數a=1,b=1,Δ=0.2,L=10,A=0.2,Ω=0.1圖3 噪聲強度D取不同值時，信噪比SNR與阻尼系數γ的關系曲線

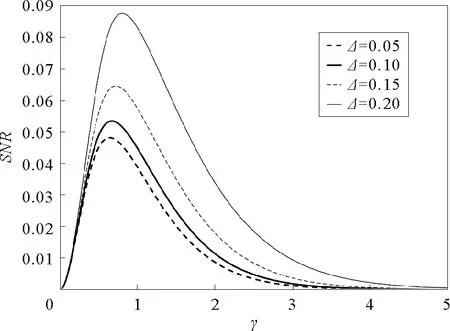
參數a=1,b=1,D=0.1,L=10,A=0.2,Ω=0.1圖4 隨機勢能的幅度Δ取不同值時，信噪比SNR與阻尼系數γ的關系曲線

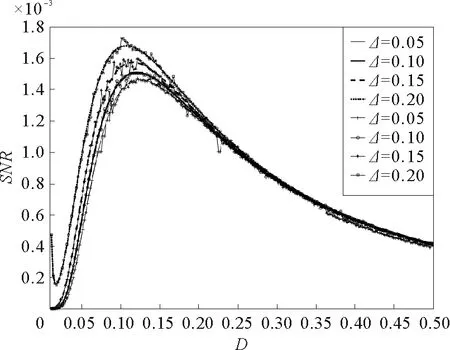
參數γ=0.1,a=1,b=0.1,L=10,A=0.1,Ω=0.1圖5 隨機勢能的幅度Δ取不同值時，信噪比SNR與噪聲強度D的關系曲線

參數a=1,b=0.1,Δ=0.2,L=10,A=0.05,Ω=0.1圖6 阻尼系數γ取不同值時，信噪比SNR與噪聲強度D的關系曲線

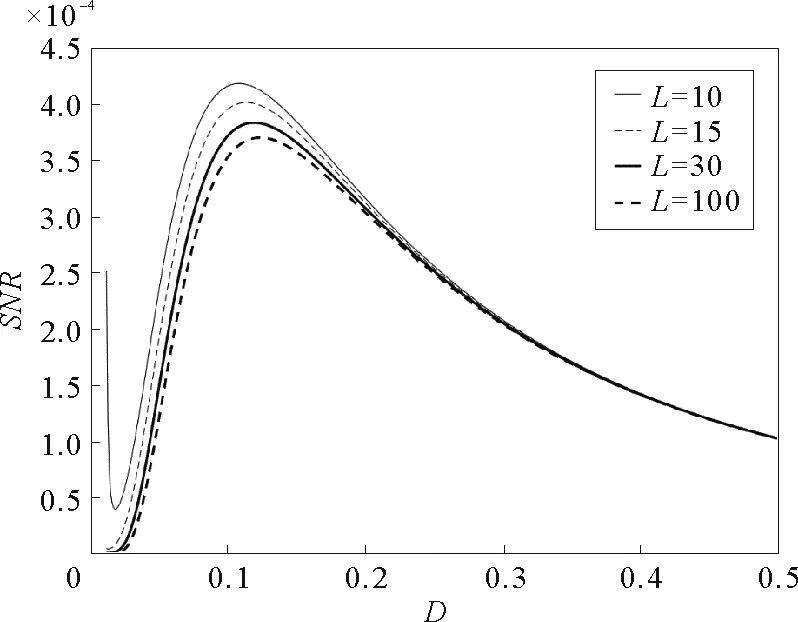
參數γ=0.1,a=1,b=0.1,Δ=0.2,A=0.05,Ω=0.1圖7 隨機勢能的相關長度L取不同值時，信噪比SNR與噪聲強度D的關系曲線

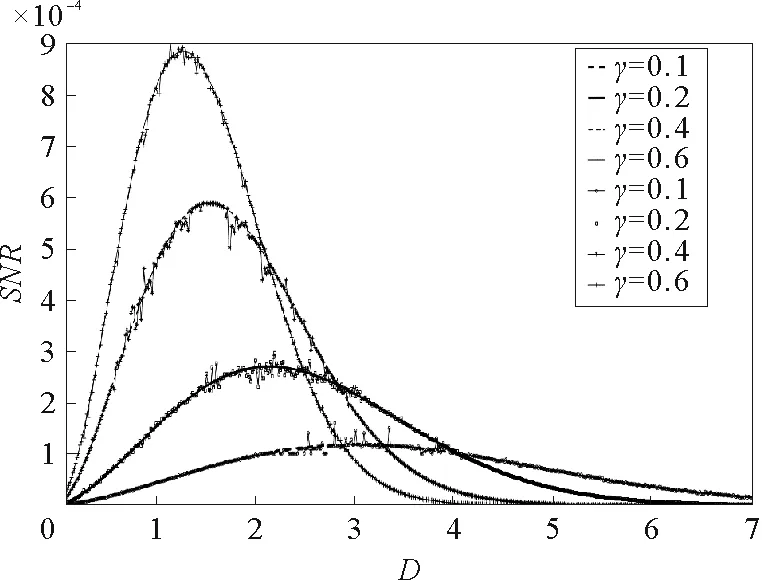
參數b=1,Δ=0.1,D=0.3,L=10,A=0.05,Ω=0.1圖8 阻尼系數γ取不同值時，信噪比SNR與系統參數a的關系曲線

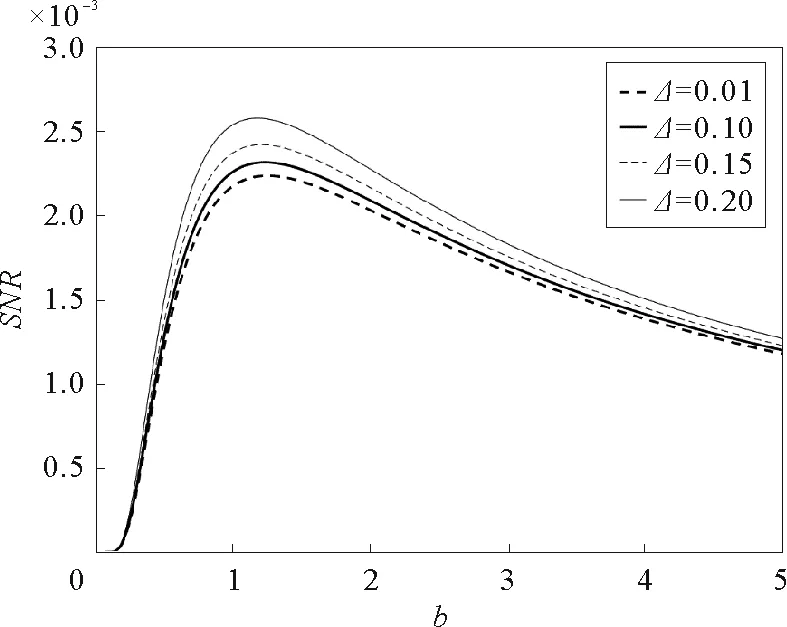
參數γ=0.1,a=2,D=0.08,L=10,A=0.1,Ω=0.1圖9 隨機勢能的幅度Δ取不同值時，信噪比SNR與系統參數b的關系曲線

為了驗證理論分析的正確性，我們對采用四階龍格—庫塔法對方程(1)進行了數值積分,計算步長為0.001。對自相關函數進行快速傅里葉變換得到輸出信號的功率譜，輸出信噪比定義為信號的頻譜與信號頻率附近噪聲功率譜的比值，部分仿真結果見圖1、圖3、圖5和圖8。由這4個圖可見，本文基于絕熱近似的理論分析結果和數值仿真結果是一致的。

3 結論

本文研究了白噪聲作用下欠阻尼隨機雙穩系統中的隨機共振現象。隨機勢能用Ornstein-Uhlenbeck噪聲建模。基于Ornstein-Uhlenbeck噪聲的統計特性和兩態理論,推導出了系統輸出信噪比的表達式。分析結果表明，在信噪比與阻尼系數的關系曲線上出現了廣義的隨機共振現象。在信噪比隨噪聲強度的變化曲線上觀察到了傳統的隨機共振現象。而且，隨著系統參數a和b的增大，信噪比也出現了共振峰。隨著隨機勢能相關長度的增大,信噪比的最大值單調減小；而隨著隨機勢能幅值的增大,信噪比的最大值單調增大。最后利用龍格—庫塔法對系統輸出信噪比進行了數值仿真。仿真結果表明，理論結論與數值分析結果是一致的。我們認為，本文研究的數學模型可以拓展雙穩系統中隨機共振的研究范圍；本文的研究結果對于具有隨機勢能的動力系統中的隨機共振分析具有一定的理論意義和參考價值。