真空環境用有刷直流電機三維瞬態溫度場的計算與分析

陳 辰，錢 華，李志鵬，秦倩倩，楊可新

(中國電子科技集團公司第二十一研究所，上海 200233)

0 引 言

有刷直流電機及其組件因體積小、轉矩大、功率密度高、控制簡單、無需外部控制電路即可正常運行的優點，而被應用于航天領域[1-2]。國內有刷電機在航天領域的應用起步較晚，相關研究多是針對無刷直流電機、步進電機等在真空環境下的溫度場分析，少有關于有刷電機真空熱分析的文獻[3-4]。真空環境下沒有對流散熱，只有熱輻射和熱傳導，因此散熱情況較常壓下差很多。電機繞組溫升影響電機的性能，過高的溫度會降低電機的可靠性，從而影響整機的使用壽命。

根據有刷直流電機的額定工況，用有限元仿真軟件對其三維溫度場進行計算，同時開展熱真空試驗，對溫度場的結果進行驗證，再將溫度場計算延伸到其他工況，可為電機的在軌使用策略提供參考依據。

本文采用有限元法計算了有刷直流電機(以下簡稱電機)的三維全域瞬態溫度場，對電機轉子槽內和端部的繞組進行了等效建模，既考慮了電機端部繞組對整個轉子的溫升影響，又降低了建模難度和計算量。根據所建立的有限元模型,分析了在負載0.075 N·m工況下電機的溫升，得到了在真空環境下電機溫度分布的規律，并結合熱真空試驗數據進行了對比和驗證。

1 瞬態溫度場的數值計算

本文所研究的電機是全封閉非密封結構形式，電機主要參數如表1所示。

表1 電機的主要數據

1.1 求解域模型的建立

1.1.1 實體分析模型的建立

建立了電機三維實體模型，對其進行了適當的模型簡化，主要是移除了電機的螺釘和螺紋孔，該部分對熱分析結果無影響。為了模擬實際使用工況，將電機熱真空試驗時使用的試驗支架也一并建模，實體模型如圖1所示。

圖1 電機組件實體模型

電機的熱量傳遞方式包括熱對流、熱傳導和熱輻射三種類型。根據傳熱學理論，求解域下三維瞬態熱傳導方程(直角坐標系)[5]：

(1)

式中：T為溫度；Kx為介質在x方向的導熱系數；Ky為介質在y方向的導熱系數；Kz為介質在z方向的導熱系數；q為熱源密度；c為熱容；γ為材料密度；τ為時間變量。

在真空中，主要通過輻射換熱實現物體表面之間的換熱。物體之間相互輻射和吸收熱量的關系可用斯蒂芬-波爾茲曼方程[6]求解：

(2)

式中：Q為熱流率;ε為輻射率；σ為斯蒂芬-波爾茲曼常數，5.67×10-8W/(m2·K4)；A1為表面1的面積；F12為表面1與表面2的之間的形狀系數；T1為表面1的溫度；T2為表面2的溫度。

1.1.2 有限元模型的建立

網格剖分采用手動剖分，分別采用了MultiZone、Sweep方法并結合面網格層數和邊尺寸的控制對溫度梯度較大和重點關心的零部件模型進行了細化剖分，獲得較好的網格單元，圖2為電機整體的剖分和內部剖分圖。

圖2 劃分網格的有刷直流電機模型

1.2 電機熱源的計算

電機在工作時，產生的損耗包括繞組銅耗、電刷接觸損耗、鐵耗、機械損耗和雜散損耗，其中大部分損耗為銅耗，本文所計算的工況中銅耗占比約40%。電機的銅耗主要是由于繞組通電產生的，電刷接觸損耗指電刷接觸電阻產生，鐵耗主要是由于磁密在定子和轉子中變化產生的。對于有刷電機，鐵耗主要產生于轉子上，機械損耗包含電刷與換向器的摩擦損耗和軸承的摩擦損耗。有刷直流電機為機械換向結構，相比于其他類型電機，在熱源構成上多出了電刷接觸損耗和電刷與換向器的摩擦損耗兩項。

轉子繞組銅損耗：

(3)

式中：I1為電機運行時的電流；R為當前溫度下的電樞電阻。

電刷接觸損耗損耗：

(4)

式中：I2為電機運行時的通過每個電刷的電流；Rds為電刷接觸電阻；n為電刷個數。

轉子鐵心損耗分為轉子軛部損耗和轉子齒部損耗：

(5)

電刷與換向器的摩擦損耗：

pdh=udsFdsv1

(6)

式中：uds為電刷摩擦系數；Fds為電刷壓力；v1為電機轉子線速度。

軸承機械損耗通過電機效率進行核算：

pf=p總-(pCu+pds+pFe+pdh)

(7)

1.3 等效導熱系數及邊界條件

1.3.1 轉子槽絕緣等效導熱系數

對轉子槽中導線、絕緣材料和端部環氧進行以下假設：槽內導線分布均勻，忽略導線間的溫差；槽絕緣材料均勻分布且全部填充；端部環氧灌封均勻且全部填充。

基于上述三點假設，把槽內所有的裸銅線當作一個整體，按照截面積等效后置于槽中心并與槽形保持一致，端部繞組用一個圓環體等效。槽絕緣材料當作另一個整體，將槽內其他空間全部填充為絕緣材料。端部環氧按照等效后的端部繞組尺寸進行填充。

圖3 電機轉子模型

槽內絕緣材料的等效導熱系數[9-10]:

(8)

式中：λeq為槽內絕緣材料的等效導熱系數(W/(m·℃))；λi為不同絕緣材料的導熱系數(W/(m·℃))；δi為不同絕緣材料的等效厚度(m)。

1.3.2 轉子鐵心等效導熱系數

轉子鐵心由硅鋼片疊加而成[9]，故根據傳熱學基本定律可得出轉子鐵心等效系數：

軸向：

(9)

徑向和周向：

λx=λy=kFeλ1+(1-kFe)λ0

(10)

式中:kFe為轉子鐵心的疊裝系數；λ1為轉子鐵心中硅鋼片的導熱系數；λ0為鐵心中絕緣材料的導熱系數。

1.3.3 邊界條件

電機外表面施加相應材料的輻射率和初始環境溫度。

2 基于有限元的溫度場計算結果

根據上述模型及條件，對電機在額定使用工況的瞬態溫度場進行仿真。該電機額定使用工況：真空30 ℃，電流0.45 A，負載0.075 N·m，轉速750 r/min。根據損耗計算公式和電機使用工況，計算得到仿真初始時刻損耗，首次仿真時假設結束時刻繞組電阻與初始時刻相同，使用該損耗計算得到電機運行180 min后的溫度場，提取出180 min時繞組溫度，對繞組電阻進行修正和迭代，經過三次迭代計算，初始繞組溫度與計算結果的誤差小于1%，確定電機180 min時的損耗分布，最終得到該電機運行180 min后的仿真結果。圖4和圖5分別為電機全域和電機內部溫度場仿真結果。

圖4 電機在0.075 N·m負載下工作180 min時全域溫度分布圖

圖5 電機在0.075 N·m負載下工作180 min時內部溫度分布圖

從圖5可以看出，該電機在30 ℃真空環境下工作180 min后，電刷溫度最高為98.7 ℃，電刷溫升為68.7 K;機殼溫度最低為51.79 ℃，機殼溫升為21.79 K;繞組溫度為71.99 ℃，溫升為41.99 K。

從圖6的電機主要部件溫度隨時間變化曲線可以看出，該電機通電后，電刷溫度迅速上升，繞組和機殼溫度上升較慢。工作60 min后，電機基本達到熱平衡，電刷與繞組的溫差維持在26 ℃左右，電刷與機殼的溫差維持在45 ℃左右。

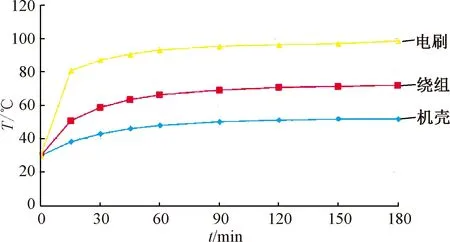
圖6 電機主要部件溫度隨時間變化曲線

電機通電后，一方面轉子運轉使得電刷與換向器間產生摩擦損耗；另一方面電刷內通過電流，在電流的作用下，使電刷與換向器間接觸電阻產生熱耗。電刷刷體體積小、熱容小，熱耗對電刷溫度影響明顯。上述兩種熱耗作用在電刷上，使得電刷迅速升溫。

電機繞組在轉子上，繞組的散熱的方式有兩種方式向外界散出：一種是通過熱輻射傳向定子、端蓋等其他結構件；另一種是通過熱傳導經由槽絕緣、鐵心、軸套、軸承、機殼傳向外界環境。真空下熱輻射傳熱能力有限，主要是熱傳導，在繞組熱傳導路徑上，軸承的熱阻較大，達到熱平衡后，繞組與機殼間溫差約19 ℃。

3 仿真結果與實測結果對比分析

將一臺樣機置于真空度≤1×10-3Pa，環境溫度為30 ℃的真空罐內，進行溫升實驗，實驗時電機(含支架)的照片如圖7所示。

圖7 實驗樣機(含支架)

在進行熱真空實驗時，電機機殼表面貼有熱敏電阻，監測機殼在實驗過程中的溫升，將檢測結果與上述仿真結果進行對比，如表1所示。

表1 仿真結果與實驗結果對比

通過表1可以看出，有限元仿真計算得到的機殼表面溫升比實驗值略高，這是由于在仿真時對模型做了一些簡化處理，機殼溫升實測值與仿真值誤差在5%左右，驗證了仿真模型的有效性和準確性?？梢詾槠渌r的仿真和實驗提供參考，同時為該類型電機的設計優化提供依據。

4 結 語

本文對電機真空下三維全域溫度場進行研究。在三維溫度場建模時考慮了繞組端部的影響，提高了繞組端部溫升計算的準確性，同時建立了包括電刷、簧片、刷架底板在內的刷架組件實體模型，通過有限元分析軟件計算額定工況(0.075 N·m)下電機的溫升，得到了電機在該工況下的全域溫度場。仿真結果表明：有刷直流電機在真空環境中溫升最高部分為電刷，電刷溫度變化的特點是通電后短時間內迅速上升，達到局部熱平衡后溫升趨于穩定。最后，對一臺樣機進行熱真空實驗，實測數據與仿真結果誤差在5%左右，滿足工程應用，證明電機模型及仿真參數設置合理可行。本文的計算與分析為直流電機電刷溫升的研究提供了支撐，對有刷直流電機的設計和優化具有一定的參考意義。