表貼式永磁電機轉子無鐵心解析法磁場分析

陳 中，劉丹丹

(鹽城工學院,鹽城 224051)

0 引 言

永磁電機的發展與貢獻在現代工業領域已成為無可爭議的焦點，無論在普通家用電器、醫療器械，還是航空航天等領域總能發現永磁電機的身影。國家2025規劃綱要明確提出，提升工業自動化的升級換代，加大在新能源領域的基礎設施建設，建設智能化節約型的現代化國家。結合永磁電機本身的特點，一般常將其分為：表貼式、表面插入式、埋入式。每一類電機都有著各自的特點，表貼式電機多用在伺服控制領域，其轉子形狀的特點并不會引起電感在直交軸分量的參數變化，便于電機的精確控制。對表面插入式電機以及埋入式電機，由于轉子磁路在物理空間上的非對稱性，轉子在旋轉過程中會引起電樞繞組中電感在直交軸上的分量發生變化，并且會產生磁阻轉矩，故在高功率密度電機應用場合被廣泛應用，如電動汽車領域。

結合磁鋼材料的發展，加工工藝的完善，從之前的鐵氧體材質，到現在的釹鐵硼的廣泛應用，給永磁電機行業帶來生機活力。永磁材料充磁方式也多種多樣，常見有徑向、平行、Halbach、正弦等。其中徑向充磁可產生梯形波的反電動勢，平行、Halbach充磁可獲得近似正弦波的反電動勢；正弦充磁可獲得較理想的反電動勢波形，但在實際充磁過程中需要的技術條件也往往比較高。因此，結合電機驅動器電流波形的特點，在無刷直流電機領域，一般采用徑向充磁；而在永磁同步電機領域，一般采用平行充磁，Halbach與正弦充磁在實際應用中需要的充磁設備條件較高。

文獻[1]采用解析方法對徑向、平行充磁進行了充分研究，但針對的是轉子有鐵心的結構。文獻[2]采用解析方法對轉子磁極形狀設計作了詳盡分析，指出轉子中注入三次諧波可提高電機轉矩輸出能力，同時也會帶來轉矩脈動增大的問題，但也是針對轉子有鐵心結構。文獻[3-4]借助解析方法，針對有鐵心結構的轉子磁極不等厚永磁采用Halbach陣列作了研究，指出Halbach充磁方式可有效提升氣隙磁密波形的正弦度，降低諧波含量。文獻[5-6]主要對梯形結構永磁在無鐵心盤式電機軸向磁場進行分析，指出梯形結構永磁在盤式電機可減小永磁的利用，增大氣隙磁密中的基波幅值，削弱磁場中的諧波含量。文獻[7]只采用有限元法對轉子有鐵心和轉子無鐵心結構進行了分析，指出轉子有鐵心結構相對無鐵心結構，可降低電機的鐵耗，提升電機的效率，但并未采用解析法進行分析。文獻[8-11]對表貼式永磁電機解析法分析了空載氣隙磁密與反電動勢的關系，并用有限元法進行了驗證，但并未對轉子無鐵心結構模型作進一步分析。

本文主要針對表貼式永磁電機轉子無鐵心的特點，結合電機電磁場的相關知識，利用麥克斯韋方程建立無轉子鐵心的解析模型，分析電機的氣隙磁密、空載反電動勢等參數，利用有限元法對解析模型進行了驗證，采用解析建模的方法可為無轉子鐵心電機磁場的設計提供一種快速分析計算的方法。

1 表貼式轉子無鐵心永磁電機的結構

本文的表貼式轉子無鐵心電機為24槽8極，電機的額定轉速設置為750 r/min。電樞繞組采用星形連接方式。在定子表面開有梨形槽，轉軸采用具有非導磁性能的合金。永磁材料選用鐵氧體。電機尺寸如表1所示。

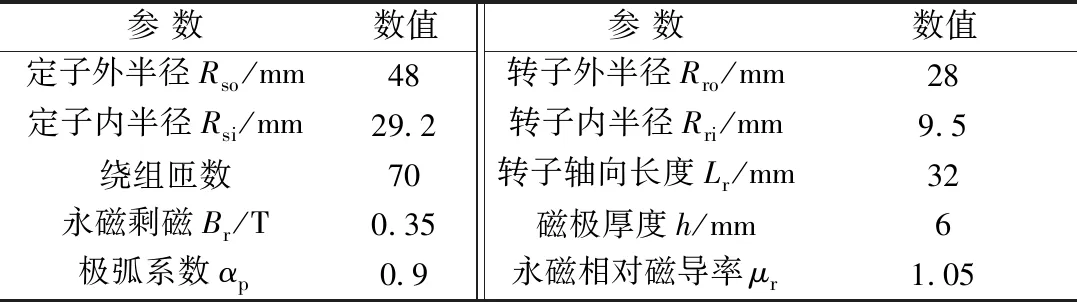
表1 電機的結構參數

電機的定轉子結構如圖1所示。

圖1 電機整體結構

2 轉子無鐵心解析法建模

2.1 轉子平行充磁分析

針對電機轉子中的永磁充磁方式，結合相關文獻，以及目前生產加工中相對成熟的工藝，電機轉子中永磁體的充磁方式選用平行充磁方式，充磁方向如圖2所示。

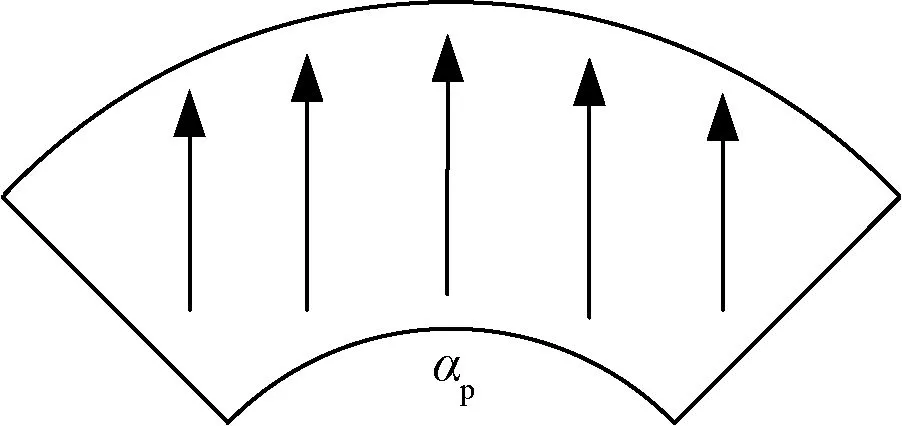
圖2 轉子平行充磁示意圖

在一對極周期內，對平行充磁沿徑向和切向方向作矢量分解，其中αp表示永磁區域在一個磁極中的有效占比。矢量分解結果為Mr和Mθ,Mr和Mθ分別為磁化強度沿著徑向和切向方向上的分量。

(1)

(2)

(3)

(4)

(5)

從上式可以看出，Mr和Mθ的數值與轉子所在的空間位置有關。

2.2 電機空載磁場建模

利用電機電磁場相關知識，首先假設電機定子內表面光滑，電機鐵磁材料內部不存在磁密飽和，且定子鐵心材料的磁導率假想為無窮大，轉子永磁磁極采用表貼式瓦片形結構，永磁材料為平行磁化，且為線性退磁特性。

結合拉普拉斯方程和準泊松方程，根據電機磁場邊界條件具有連續變化的特點，可將整個電機的區域劃分為以下幾個區域：電機氣隙磁場區域Ⅰ，轉子永磁體區域Ⅱ，轉子無鐵心區域Ⅲ。電機磁場劃分區域如圖3所示。

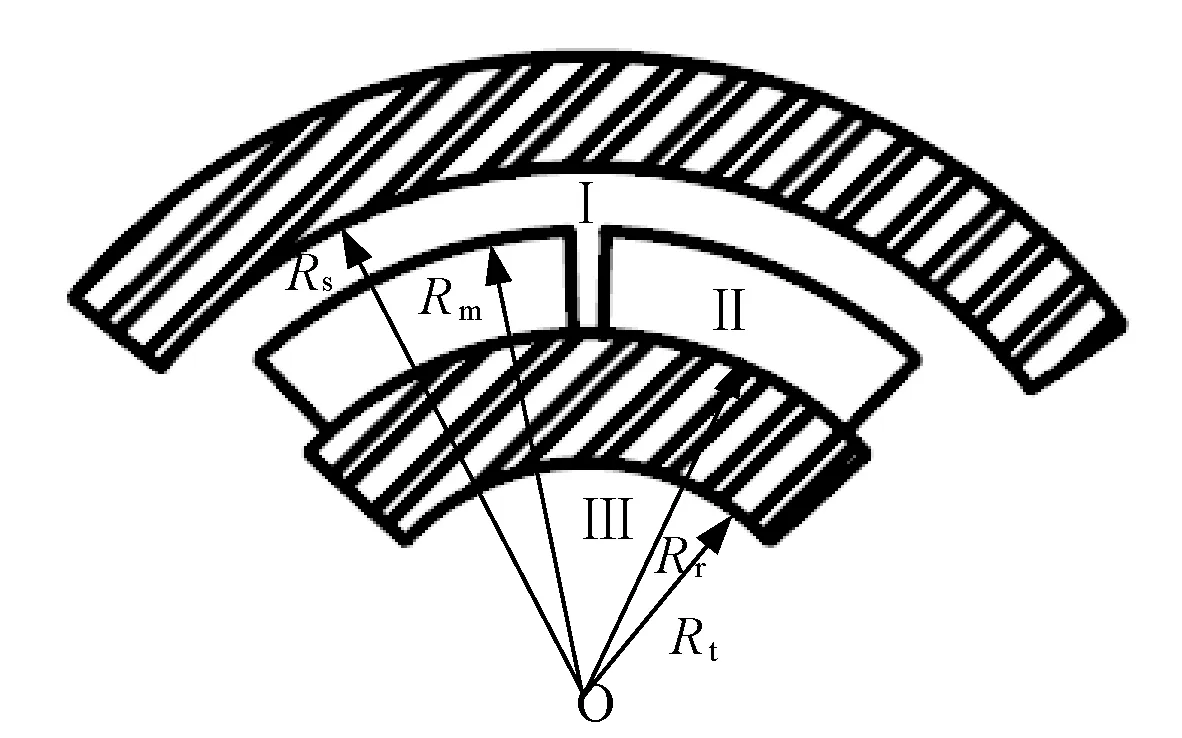
圖3 磁場分析區域劃分

在圖3中，永磁體厚度是由Rm和Rr決定的，Rt表示鐵心的半徑，當Rt=0時，表示電機無轉子鐵心，Rs表示定子的內半徑尺寸。

對于氣隙區域以及永磁體區域，它們的標量磁位方程則有如下關系：

(6)

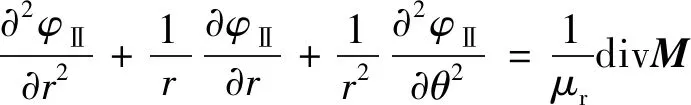
(7)

(8)

磁場強度H在徑向和切向方向上的分量具有下列關系：

(9)

同時，將磁化強度M寫成矢量分解求和的形式:

M=Mrer+Mθeθ

(10)

式中：Mr和Mθ分別為磁化強度沿著徑向和切向方向上的分量。

磁場強度H與磁感應強度Br在磁場邊界處需滿足如下關系，

(11)

為便于計算，可將磁化強度分量寫成級數累加的形式:

(12)

(13)

同時，將電機的轉子磁極沿圓周對每一極進行劃分，則每極占有π/p機械角度，由于一對磁極中包含N和S極，即存在下列關系：

(14)

進一步對磁化強度求散度計算，則滿足下列關系：

(15)

結合上述微分方程及磁場的邊界條件，聯立后可得徑向和切向氣隙磁密表達式：

(16)

(17)

式中：

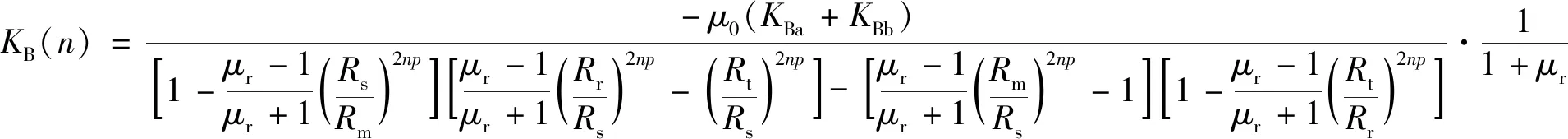
(18)

(19)

(20)

(21)

(22)

3 轉子無鐵心空載氣隙磁場的分析

從圖1中看出，電機定子結構部分開有梨形槽，定子內表面是非光滑連續，氣隙磁密在定子齒尖處會發生畸變，造成磁密中的諧波含量增加，引發電磁噪聲、電磁振動等問題。

在采用解析法分析表貼式永磁電機轉子無鐵心問題時，已假設定子內表面光滑連續。為了便于驗證解析模型的正確性，采用有限元法對其進行驗證，但在實際計算時，有限元法必須對電機模型作適當修改，簡化為定子內表面光滑連續。

圖4是采用有限元法獲得的電機徑向氣隙磁密，分別分析了考慮定子齒槽效應和忽略定子齒槽效應(需對定子內表面作適當修改，保持定子內半徑不變)兩種情況。

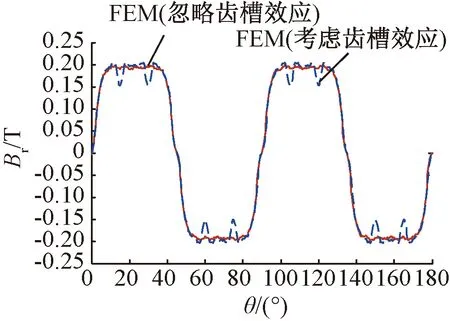
圖4 考慮齒槽效應與忽略齒槽效應時有限元法獲取的徑向氣隙磁密波形對比

從圖4中可以看出，氣隙磁密波形在定子開口處出現非光滑下凹的現象，發生了部分畸變。當忽略定子齒槽時，氣隙磁密波形仍保持光滑連續。由此可以得出，定子開槽破壞了電機氣隙長度的均勻性，由于鐵磁導率遠大于空氣磁導率，磁密波形在接近定子槽口處磁通路徑必然要發生一定的改變，造成氣隙磁密波形中諧波成分的增加。

對圖4的考慮定子齒槽效應以及忽略定子齒槽效應的磁密波形分別作FFT分析，如圖5所示。

圖5 空載徑向氣隙磁密FFT分析

從圖5中可以看出，在定子開槽情況下獲得徑向氣隙磁密基波幅值為0.233 3 T，總諧波為27.59%。當忽略定子齒槽效應時，定子內表面光滑，獲得的徑向氣隙磁密基波幅值為0.236 9 T，磁場中的諧波含量占25.48%。對比分析可知，在電機定子結構上開槽，會降低磁密的基波幅值，增大THD。

同樣，采用有限元法獲得的電機切向氣隙磁密如圖6所示。

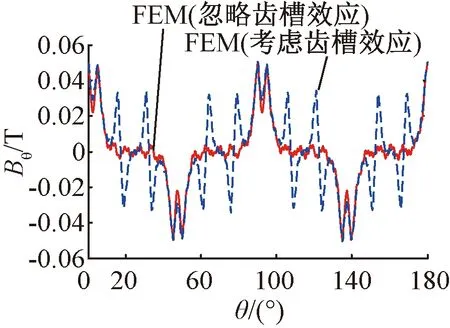
圖6 考慮齒槽與忽略齒槽效應時有限元法獲取的切向氣隙磁密波形對比

從圖6中可以看出，切向氣隙磁密波形反映了定子齒槽結構的影響，定子開槽波形變化非常明顯，主要是由于在定子各個齒尖處磁密中的切向分量變化比較迅速，加劇了磁場中的諧波含量。

上述分析都是基于有限元法，為了便于突出所建立解析分析法的準確性，以下分析選用忽略電機定子齒槽效應的結構。在電機參數完全一致的情況下，解析法與有限法獲得的徑向氣隙磁密波形如圖7所示。

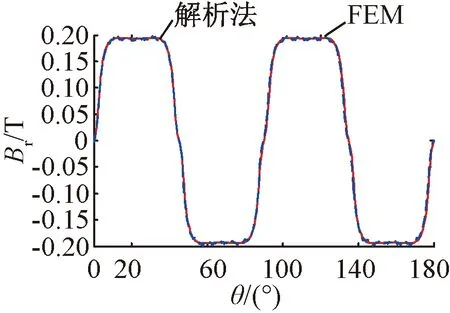
圖7 解析分析法與有限元法獲得的徑向氣隙磁密波形比較

采用同樣的分析方法，獲得的電機切向氣隙磁密波形如圖8所示。

圖8 解析分析法與有限元法獲得的切向氣隙磁密波形比較

從圖7和圖8中可以看出，對于電機轉子無鐵心結構模型，解析法與有限元法獲得的電機徑向、切向氣隙磁密波形完全一致，驗證所建立的轉子無鐵心電機空載磁場的解析法的準確性。

利用所建立的解析分析模型，僅改變表1中電機的極弧系數αp，永磁采用平行充磁，獲得電機的徑向氣隙磁密曲線，并對其作FFT分析，磁密的基波幅值與THD隨αp的變化規律如圖9所示。

圖9 磁密基波與THD隨αp的變化規律

從圖9中可以看出，徑向氣隙磁密的基波幅值隨著極弧系數αp的增大而增大，總諧波THD隨著αp的增大出現先減小后增加的趨勢，當αp在0.75～0.8之前時可獲得較低的THD。因此，電機在設計時選取合適的極弧系數可有效降低氣隙磁場中的諧波含量。

從以上分析中可以看出，解析法相對有限元法具有快速計算的特點，在分析處理相關變量時非常簡便，獲取參數變化對磁密的影響也更清晰。因此借助解析法分析轉子無鐵心的空載磁場分布更具有優勢。

4 空載反電動勢分析

電機在空載場下相反電動勢是反映電機電磁狀態的關鍵參量，在電機設計時必須對其充分討論。

根據電磁學相關知識，一個導電線圈所產生的磁通量[10-11]：

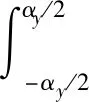
(23)

式中：αy表示為繞組的節距；l代表電機的軸向長度。

結合繞組磁鏈與相反電動勢的關系可知：

(24)

Kdpn=Kpn·Kdn

(25)

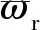
(26)

從繞組的相反電動勢解析式中可以看出，相反電動勢大小與線圈繞組的匝數、電機定子內徑尺寸、轉速、繞組因數、磁密幅值、電機軸向長度等參數有關。

采用解析法與有限元法獲得的相反動勢波形如圖10所示。

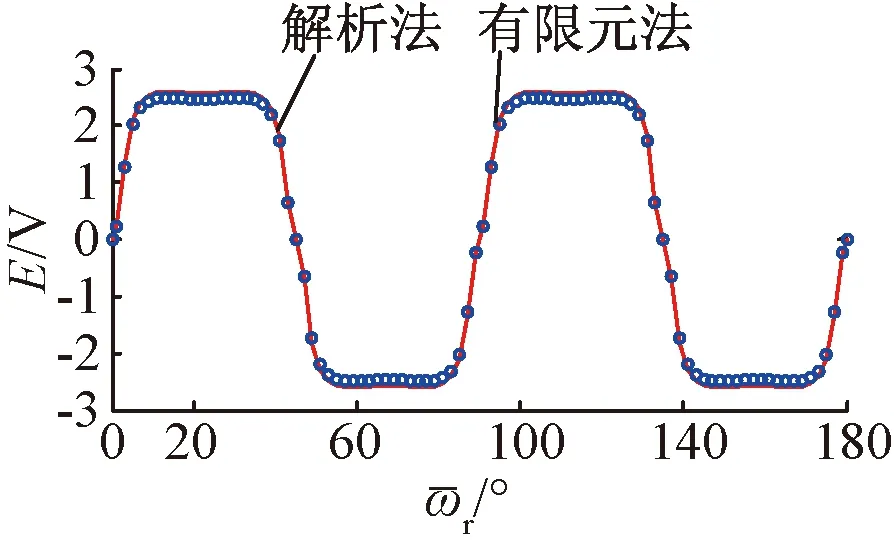
圖10 解析法與有限元法獲得的空載反電動勢

從圖10中可以看出，對于轉子無鐵心結構，解析法與有限元法對相反電動勢的分析基本一致，但在曲線吻合度上稍有些差異，沒有氣隙磁密曲線的分析結果更精確。主要原因歸于，作用在繞組中的磁勢主要來源于磁密中的徑向分量，轉子在旋轉過程中切割線圈，繞組也會受繞組分布系數、節距系數的影響，另外解析法在實際計算反電動勢時，是由一系列級數累加而成，選取的多少會影響到曲線的逼近程度。但從整體變化趨勢以及反電動勢幅值可以看出，用解析法計算反電動勢仍是可行的。

5 結 語

本文主要針對表貼式轉子無鐵心永磁電機結構，轉子永磁采用平行充磁方式，借助有限元法對考慮定子齒槽效應以及忽略定子齒槽效應的電機空載磁場進行討論。同時，為了便于解析建模，對電機磁場的邊界條件進行簡化，解析法在分析時忽略了定子齒槽效應的影響。研究結果表明，對于轉子無鐵心結構，采用解析法獲得的徑向和切向磁密波形與有限元法完全一致，在求解反電動勢時與有限元法曲線的擬合度上存在細微差異，但對反電動勢波形的幅值并無無實質的影響。相比于有限元法，解析法在改變電機參數變量獲取相關變化規律時具有很強的時效性，因此在表貼式轉子無鐵心電機結構的設計過程中具有一定的實際應用價值。