基于差分進化算法的自行高炮隨動系統PID參數整定

孫國軒，宮新宇，時巖，謝繼鵬，魯斌

(1.南京理工大學 機械工程學院，江蘇 南京 210094；2.63850部隊，吉林 白城 137001)

0 引言

高炮行進間瞄準目標時，路面不平度引起的車體姿態變化，將影響其隨動控制系統性能，進而影響高炮射擊精度，因此建立行進間精確高炮隨動系統控制模型、研究其控制參數整定方法至關重要，是保證高炮行進間命中目標的基礎。文獻[1]考慮了構件間的剛柔耦合等非線性因素建立高炮行進間發射動力學模型，分析行進間射擊炮口響應規律。文獻[2]建立了路、車、炮一體化動力學模型，分析行進間路面激勵和車體俯仰運動對炮口振動的影響。文獻[3]基于剛柔耦合及接觸碰撞算法建立坦克行進間剛柔耦合多體動力學模型，研究炮口振動對坦克行進間射擊精度的影響。文獻[4]建立了某防御戰車剛柔耦合動力學模型，研究戰車行進間射擊時路面及車速對炮口擾動的影響。文獻[5]采用駐退機力加載方法和剛柔耦合技術建立了輪式自行突擊火炮行進間射擊虛擬樣機，分析行進間炮口和觀瞄位置動態響應對射擊精度的影響。以上文獻主要討論行進間炮口振動對射擊精度的影響。文獻[6]建立了高炮俯仰姿態變化的數學模型，分析不同路面下高炮隨動誤差的分布特性。文獻[7]考慮路面對車體姿態角的影響，研究了按擾動補償的復合控制算法，進一步提高了行進間隨動系統的控制精度。文獻[8]提出采用速率陀螺儀測量車體姿態變化，作為前饋加入到隨動系統中，試驗表明該方法有效可行。以上文獻均通過數學模型分析行進間隨動系統控制精度。文獻[9]中采用的徑向基函數(RBF)神經網絡滑模控制方法，進一步提高了坦克炮控系統的動態與靜態性能。文獻[10]針對坦克行進間顛簸路面影響身管穩定性的問題，利用神經網絡對非線性擴張狀態觀測器的參數進行在線整定，提高了系統的魯棒性。但上述方法計算復雜度較高，本文研究對象的處理器不能達到這些算法的要求。

針對上述問題，本文以某高炮為研究對象，建立了考慮行進間車體姿態擾動的隨動控制系統模型，并結合上裝虛擬樣機建立隨動系統的機電聯合仿真模型。在此基礎上，利用差分進化算法整定PID控制參數，對比分析參數整定前后高炮行進間火力線的控制精度及穩定性。

1 自行高炮隨動控制系統建模

1.1 隨動控制系統基本結構

該隨動控制系統由伺服電機、脈沖寬度調制(PWM)變換器、控制器、傳感器等部件組成。本文建立了由位置環、速度環和電流環構成的三閉環結構形式的隨動控制系統模型，其仿真結構框圖如圖1所示。圖1中：θi為輸入信號；θo為輸出信號。

圖1 隨動系統結構框圖Fig.1 Block diagram of servo system

1.1.1 執行電機

伺服電機為隨動系統中的執行機構，將電信號轉換成炮塔和起落部分所需的驅動力矩。建模時，基于電阻、電感、轉矩系數、轉動慣量和負載轉動慣量等參數構建伺服電機模塊，與電流調節器和速度調節器構成電流環和速度環，其數學模型如下。

電機電樞回路電壓平衡方程為

(1)

式中：Ua為電樞電壓；E為電機感應電動勢；Ia為電樞電流；R為主電路總電阻；L為主電路總電感。

電機感應電動勢為

E=Cen，

(2)

式中：Ce為電動勢系數；n為電機轉速。

電磁轉矩為

Te=CmIa，

(3)

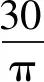
電機軸上動力學方程為

(4)

式中：TL為負載轉矩；Jd為拖動裝置等效至電機軸上的轉動慣量。

在零初始條件下對上述公式進行拉普拉斯變換，得到電壓與電流、電流與電動勢、電動勢與電機轉速間的傳遞函數分別為

(5)

(6)

(7)

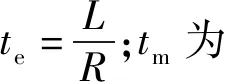
根據(5)式～(7)式搭建執行電機模型，得到其動態結構框圖如圖2所示。

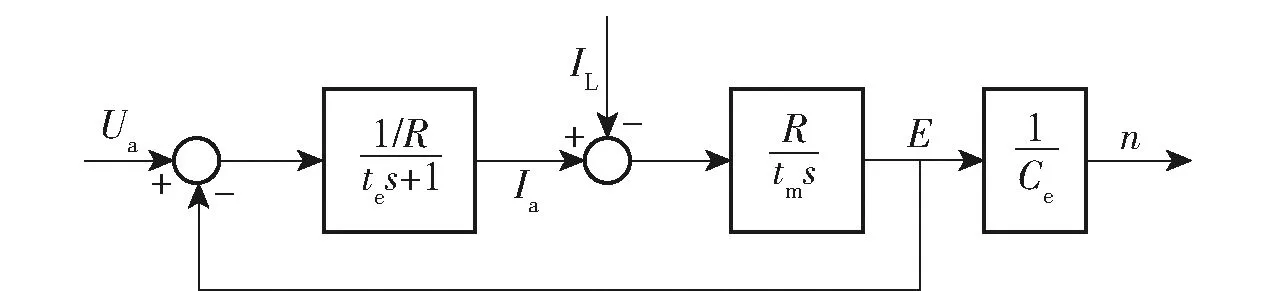
圖2 電機動態結構框圖Fig.2 Dynamic structure diagram of motor

1.1.2 電流環

圖3 電流環結構框圖Fig.3 Structure diagram of current loop

典型Ⅰ型系統具有超調量小、穩定性好等優點，因此將電流環設計為典型Ⅰ型系統，電流調節器WACR設計為PI調節器，其傳遞函數為

(8)

由于PWM變換器開關頻率一般在10 kHz以上，因此計算時將其看作1階慣性環節。

1.1.3 速度環

圖4 速度環結構框圖Fig.4 Structure diagram of speed loop

設計該環時，為實現系統無靜差，將其設計為Ⅱ型系統。速度調節器WASR設計為PI調節器，其傳遞函數為

(9)

1.1.4 位置環

位置環為隨動控制系統的最外環，設計時將電流環和速度環作為內環進行設計，其結構框圖如圖5所示。圖5中：WAPR為位置控制器；r為減速器的傳動比。

圖5 位置環結構框圖Fig.5 Structure diagram of position loop

1.2 射擊諸元解算

與停止間瞄準目標不同，自行高炮在行進間進行瞄準時，車體與目標間的距離以及路面不平度引起的車體姿態變化會對火力線的控制產生影響。因此在控制模型中加入坐標轉換模塊，用于實時解算射擊諸元。

車輛行駛時車體坐標系隨下座圈運動，目標在大地坐標系中的坐標為(x，y，z)，通過(10)式和(11)式變換到車體坐標系下的坐標為(x′，y′，z′)。

(10)

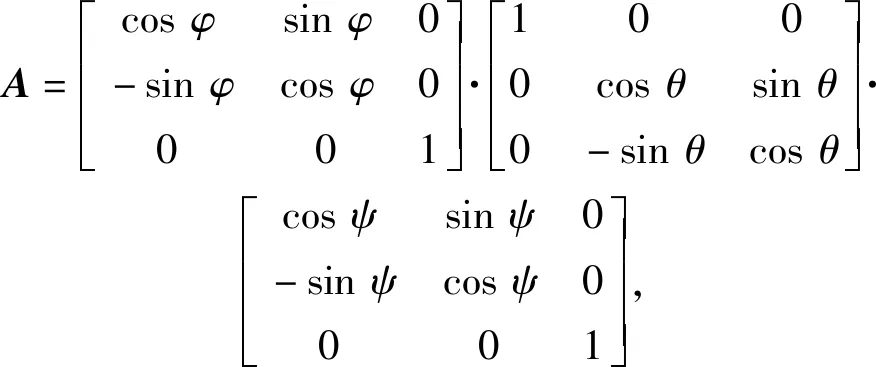
(11)

式中：(xr，yr，zr)為車體坐標系相對于大地坐標系的坐標，仿真時從動力學模型中測量得到；φ、θ、ψ分別為車體姿態變化導致的車體坐標系相對于大地坐標系產生的章動角、進動角和自轉角。

目標在車體坐標系中的方向角β和高低角α為

(12)

(13)

式中：a為耳軸中心與車體坐標系Oxy平面間的距離；b為耳軸中心與車體坐標系z軸間的距離。

1.3 隨動系統控制策略

1.3.1 分區式PID控制

本文所研究的被控對象具有較大的轉動慣量，為兼顧系統的動態性能與穩態精度，位置環采用分區式PID控制策略，即根據誤差大小將其分為不同區域，各區域大小根據調炮速度和加速度要求進行劃分，如圖6所示，位置控制器根據誤差所在區域使用不同的控制算法或控制參數。

圖6 方向/高低角誤差分區示意圖Fig.6 Schematic diagram of azimuth/elevation angle errors

各區域所采用的控制策略如下：

1) Ⅲ區為大誤差區域。當誤差處于該區域時位置控制器采用Bang-Bang控制策略，使系統快速地向減小誤差的方向運動，提高系統的動態性能。

2) Ⅱ區為中誤差區域。當誤差處于該區域時應逐步減小電機速度，防止系統直接從Ⅲ區進入Ⅰ區出現大振蕩。因此本文對該區采用PD控制策略，避免系統出現過大超調量。

3) Ⅰ區為小誤差區域。當系統跟蹤動目標時誤差均處在該區域，因此采用PID控制策略，提高系統的控制精度，保證系統的穩態誤差要求。

1.3.2 速度補償

對于三環控制系統，其外環截止頻率要低于內環，只在位置環考慮車體姿態角的影響并不能獲得較好的響應速度。因此，本文在控制模型的速度環中引入由姿態角變化引起的高低/方向角速度變化量作為速度補償，以提高系統的響應速度。對航向角、橫搖角和縱搖角速度進行變換，得到方向角速度補償和高低角速度補償分別為

ωβ=(-ωysinβ-ωxcosβ)tanα-ωz，

(14)

ωα=-ωycosβ+ωxsinβ，

(15)

式中：ωβ為方向角速度；ωα為高低角速度；ωx為橫搖角速度；ωy為縱搖角速度；ωz為航向角速度。

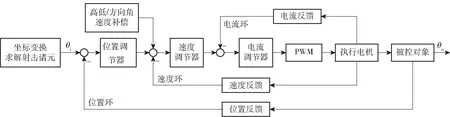
圖7 行進間隨動系統結構框圖Fig.7 Block diagram of servo system on the move

1.4 聯合仿真模型搭建

基于上裝虛擬樣機與隨動控制系統之間的信息交互，用高炮上裝動力學模型代替高炮上裝等效解析數學模型，實現機電聯合仿真分析，能夠充分考慮構件間接觸、力元等因素對仿真結果的影響，提高仿真的精確度。

1.4.1 高炮上裝動力學建模

高炮上裝由起落部分、炮塔、供彈系統組件和下座圈(車體)4部分組成，利用鉸描述各部分的連接關系，包括旋轉副、固定副、接觸碰撞等，用hi表示，其拓撲結構如圖8所示。炮塔與下座圈之間通過旋轉副h1定義其轉動關系，使炮塔可繞下座圈中心轉動。起落部分相對于炮塔可繞耳軸軸線轉動，二者之間的轉動關系通過旋轉副h2定義，同時建立二者間的接觸碰撞h3. 供彈系統、方向機、高低機等部件通過固定副h4、h5、h6與炮塔固定連接，其質量和轉動慣量通過計算等效至炮塔。方向機力矩和炮塔轉動時產生的阻力矩施加于下座圈中心處。高低機力矩、起落部分轉動時產生的阻力矩和平衡機力矩施加于耳軸中心處。

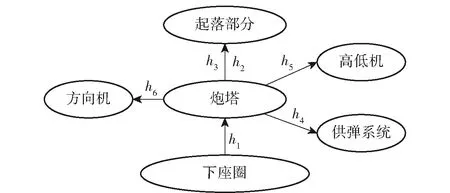
圖8 高炮上裝拓撲結構Fig.8 Topological structure of antiaircraft gun

為更加準確模擬試驗路面條件且便于試驗與仿真結果對比，試驗中直接采集下座圈處x軸、y軸、z軸3個方向上車體的位移信息和車體姿態角信息，包括航向角、橫搖角和縱搖角。仿真時將采集到的數據以點驅動的方式施加在下座圈處。

建模時，大地坐標系原點取下座圈下平面中心，平行于地面指向車輛前方為x軸正向，指向駕駛員右側為y軸正向，垂直指向下方為z軸正向，滿足右手定則。初始狀態下，車體坐標系與大地坐標系重合。

1.4.2 變量設定

變量用于實現動力學模型與控制系統模型之間數據的相互調用，分輸入變量和輸出變量。設置高低機力矩和方向機力矩為輸入變量，驅動炮塔和起落部分轉動。設置高低/方向角位移、高低/方向角速度、車體姿態、目標在大地坐標系中的坐標值為輸出變量，為隨動系統提供輸入信號，計算相應誤差下的輸入力矩。變量調用示意圖如圖9所示。

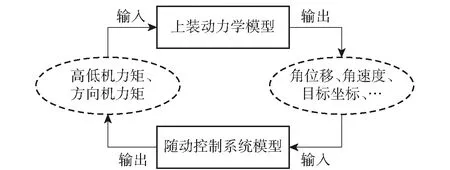
圖9 變量調用示意圖Fig.9 Schematic diagram of variable calling

至此，得到完整的隨動控制系統聯合仿真模型如圖10所示。

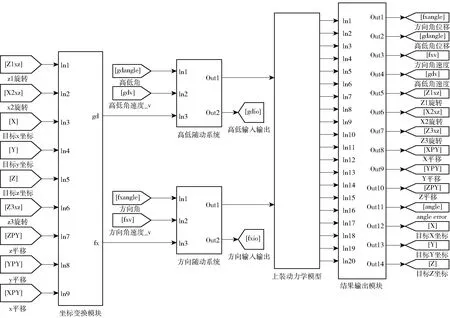
圖10 聯合仿真模型Fig.10 Co-simulation model

1.5 試驗驗證

為驗證所建聯合仿真模型的正確性，將實車試驗結果與仿真結果進行對比分析。試驗中在距離車輛正前方50 m處設立一個高為2.6 m的目標靶，初始時刻高炮火力線瞄準靶心，車輛以約1.67 m/s的速度正對目標靶行駛。試驗中對車速、航向角、縱搖角、橫搖角、火力線相對于車體的方向角和高低角等參數進行采集。仿真中，設置目標坐標為(50 000 mm,0 mm,-500 mm)，模型中大地坐標位于下座圈中心，所以此處z軸坐標設置為-500 mm，與試驗條件相符。車體運動規律數據包括車體在x軸、y軸、z軸方向上的位移信息以及車體航向角、橫搖角、縱搖角信息，如圖11～圖14所示，仿真時通過點驅動方式施加于下座圈中心。

看來，對方相貌雖兇，到底還是有些忌憚師父的。青辰暗暗松了口氣，正要從樹后走出，卻忽然發現，在對方轉身邁出幾步之后，那垂落在腰間的左手，掌心似乎有什么東西動了一下。

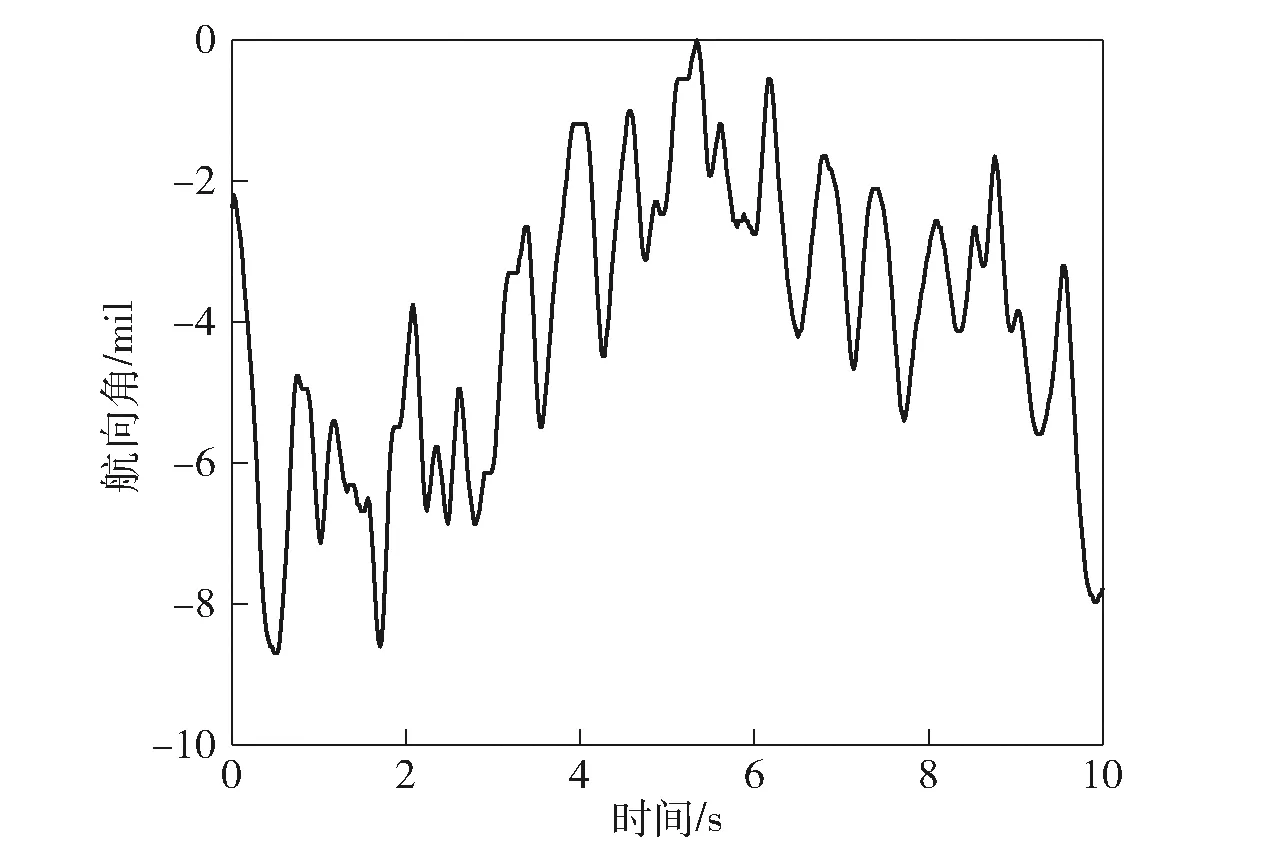
圖11 航向角Fig.11 Course angle

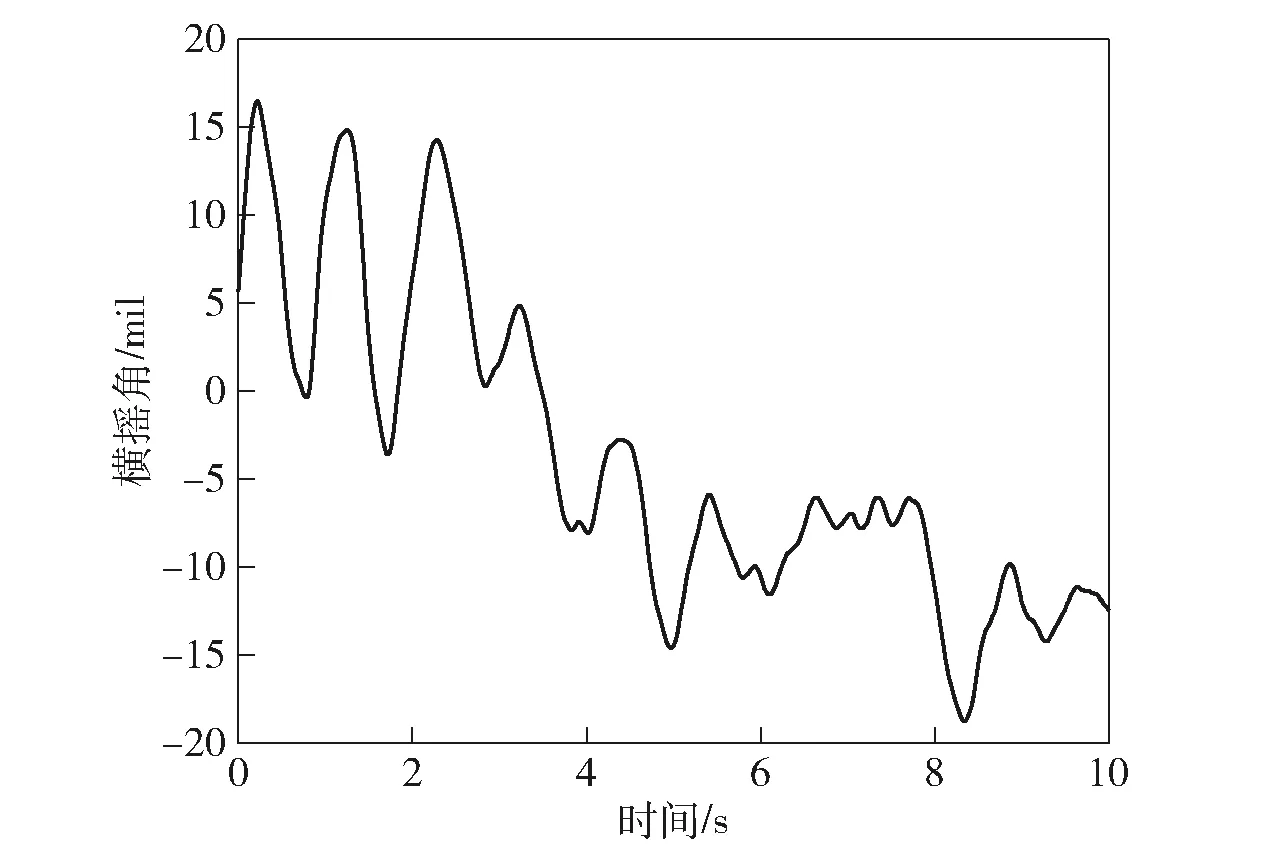
圖12 橫搖角Fig.12 Roll angle

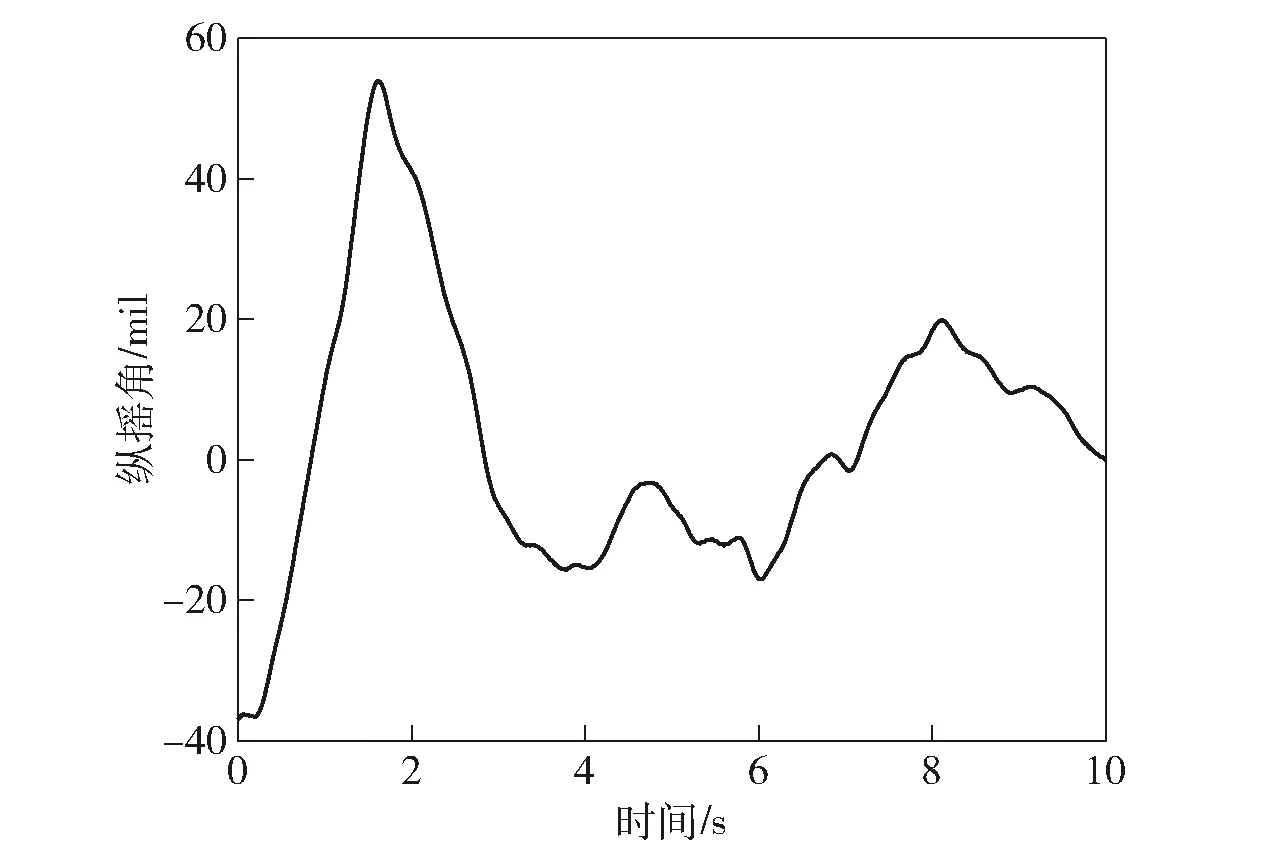
圖13 縱搖角Fig.13 Pitch angle

圖14 z軸方向位移Fig.14 Z-direction displacement

試驗結果與仿真結果對比分別如圖15、圖16、表1所示。通過對比發現：火力線高低角位移曲線和方向角位移曲線的仿真結果與試驗數據基本一致，二者運動規律一致，最大位移相對偏差較小；兩組試驗數據與仿真數據相關系數分別達到0.97和0.98，具有強相關性，說明該聯合仿真模型具有一定的準確性，可為進一步分析火力線的控制精度和穩定性以及優化PID參數提供依據。

表1 仿真與試驗結果數值對比Tab.1 Numerical comparison of simulated and test results

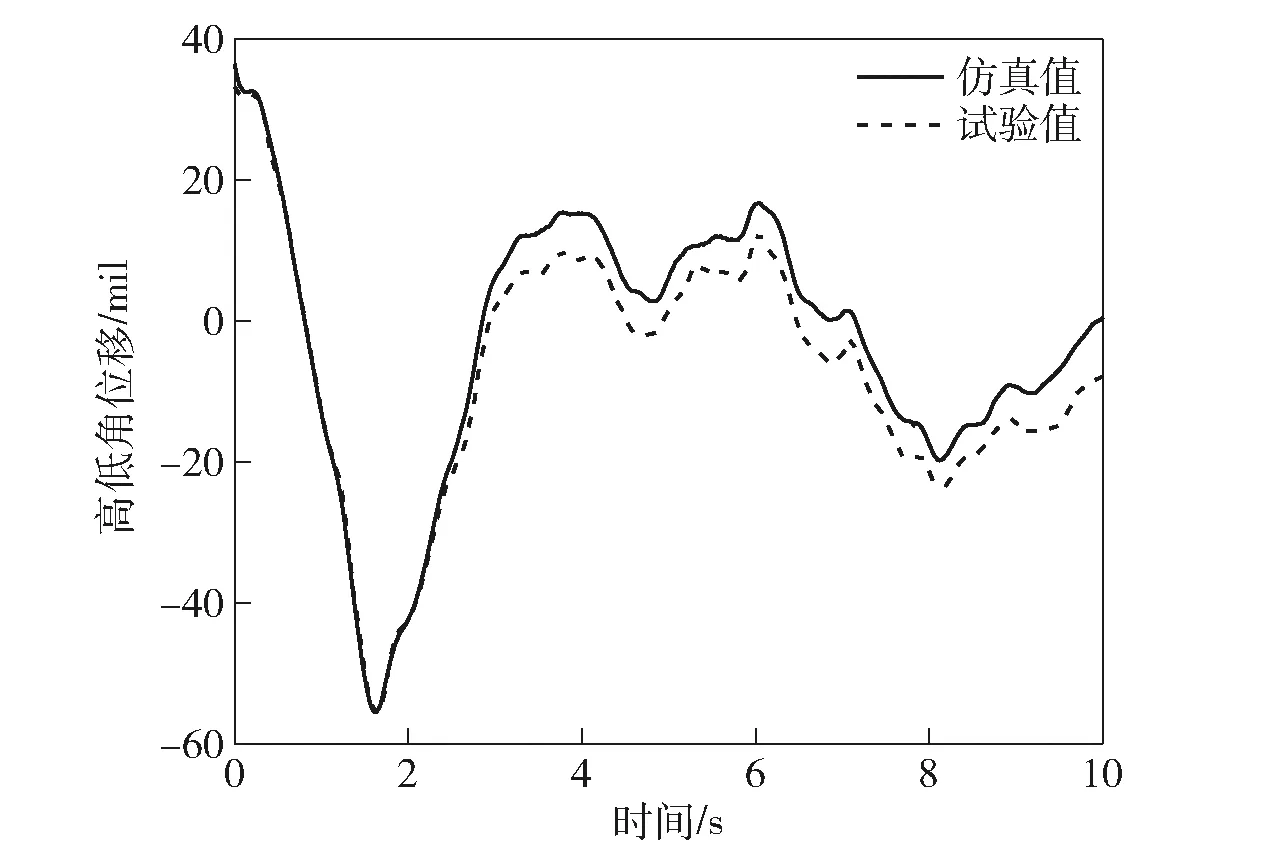
圖15 高低角位移對比Fig.15 Comparison of elevation angle displacements

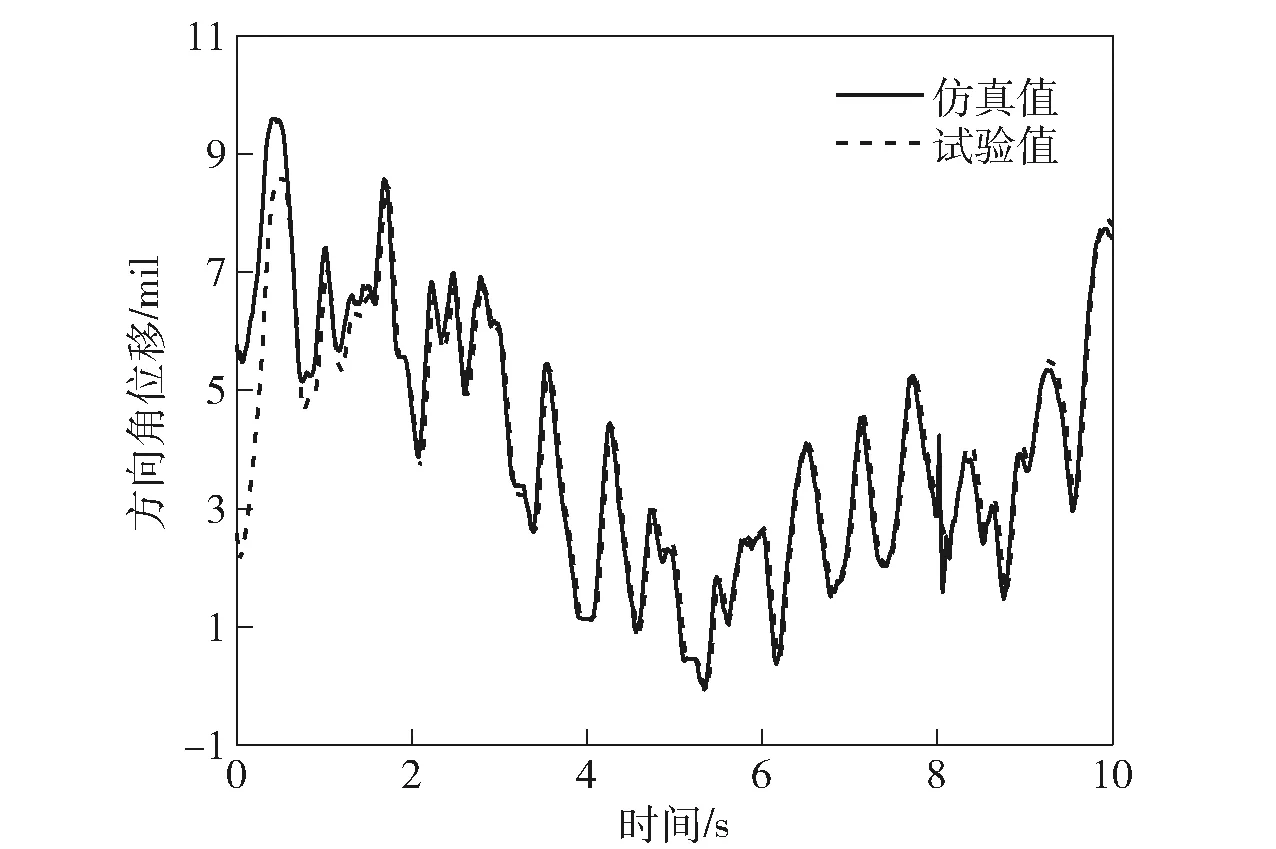
圖16 方向角位移對比Fig.16 Comparison of azimuth displacements

2 PID參數整定

行進間路面不平度引起的車體姿態變化導致方向/高低射角處于實時波動的狀態，且隨著車速增加和路面條件變差波動會更加頻繁，這就對隨動系統響應的快速性和精確性提出了更高的要求。而PID參數作為影響系統控制精度的主要因素之一，對其進行整定至關重要。傳統PID參數整定方法存在工作量大、效率低等缺點，難以整定得到較好的控制參數。因此，本文利用智能優化算法對PID參數進行整定，提高行進間隨動系統的控制精度和魯棒性。

2.1 差分進化算法

差分進化(DE)算法由Storn和Price于1995年提出，是一種以適者生存為原則的隨機啟發式搜索算法[13-14]。DE算法是基于實數編碼的優化算法，由變異、交叉和選擇3個基本操作構成，主要包括以下4個步驟：

步驟1生成初始種群。基于for循環和rand函數，根據(16)式在N維空間中隨機生成M個個體構成初始種群，其中N為待優化參數個數。

(16)

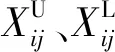
步驟2變異操作。由ceil函數和rand函數生成3個隨機數q1、q2、q3，并由while循環和或運算保證i≠q1≠q2≠q3，對應的3個個體Xq1、Xq2、Xq3通過差分方式完成(17)式所示的變異操作。

Hij(t+1)=Xq1j(t)+F·(Xq2j(t)-Xq3j(t))，

(17)

式中：Hij(·)為新生成的變異個體；F為變異因子；Xq1j、Xq2j、Xq3j為從群體中隨機選取的個體。為提高優化效率，本文Xq1j使用上一代中的最優個體。

步驟3交叉操作。DE算法通過從上一代個體和變異個體中選取元素的方式進行交叉操作，以保證群體的多樣性，增強算法對局部區域的搜索能力。由rand函數生成0～1之間的隨機數與交叉概率進行比較，判斷新個體中元素的來源。

(18)

式中：Vij(·)為新生成的個體；CR為交叉概率。

本文為保證算法初期種群的多樣性以及較大搜索范圍，采用較大的變異因子和較小的交叉概率。為提高算法后期搜索精度和收斂速度，采用較小的變異因子和較大的交叉概率。因此仿真中對變異因子和交叉概率進行(19)式和(20)式所示的線性調整。

(19)

(20)

式中：Fmax、Fmin為變異因子上限、下限；CRmax、CRmin為交叉概率上限、下限；G為最大進化代數；g為當前進化代數。

步驟4選擇操作。通過對比父代個體與子代個體的適應度值，選取適應度值較小的個體進行下一代搜索，完成選擇操作。

(21)

式中：f(·)為適應度函數。

2.2 適應度函數選取

本文仿真工況考慮了路面不平度對車體姿態的影響，輸入信號并不是單一的控制信號，因此采用誤差泛函積分評價指標作為該算法的適應度函數。誤差積分準則中，時間t乘以誤差e(t)絕對值積分(ITAE)準則具有較好的實用性和選擇性，且按此準則設計的控制系統瞬態響應振蕩小，能夠兼顧快速性和穩定性要求[15]，因此本文選取ITAE準則作為優化算法的適應度函數，其數學表達式為

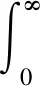
(22)

根據上述步驟編寫DE算法，建立優化算法與聯合仿真模型之間的數據交互，自動修改隨動系統中的PID參數并調用該組參數仿真得到的ITAE指標值。完整的DE算法流程圖如圖17所示。

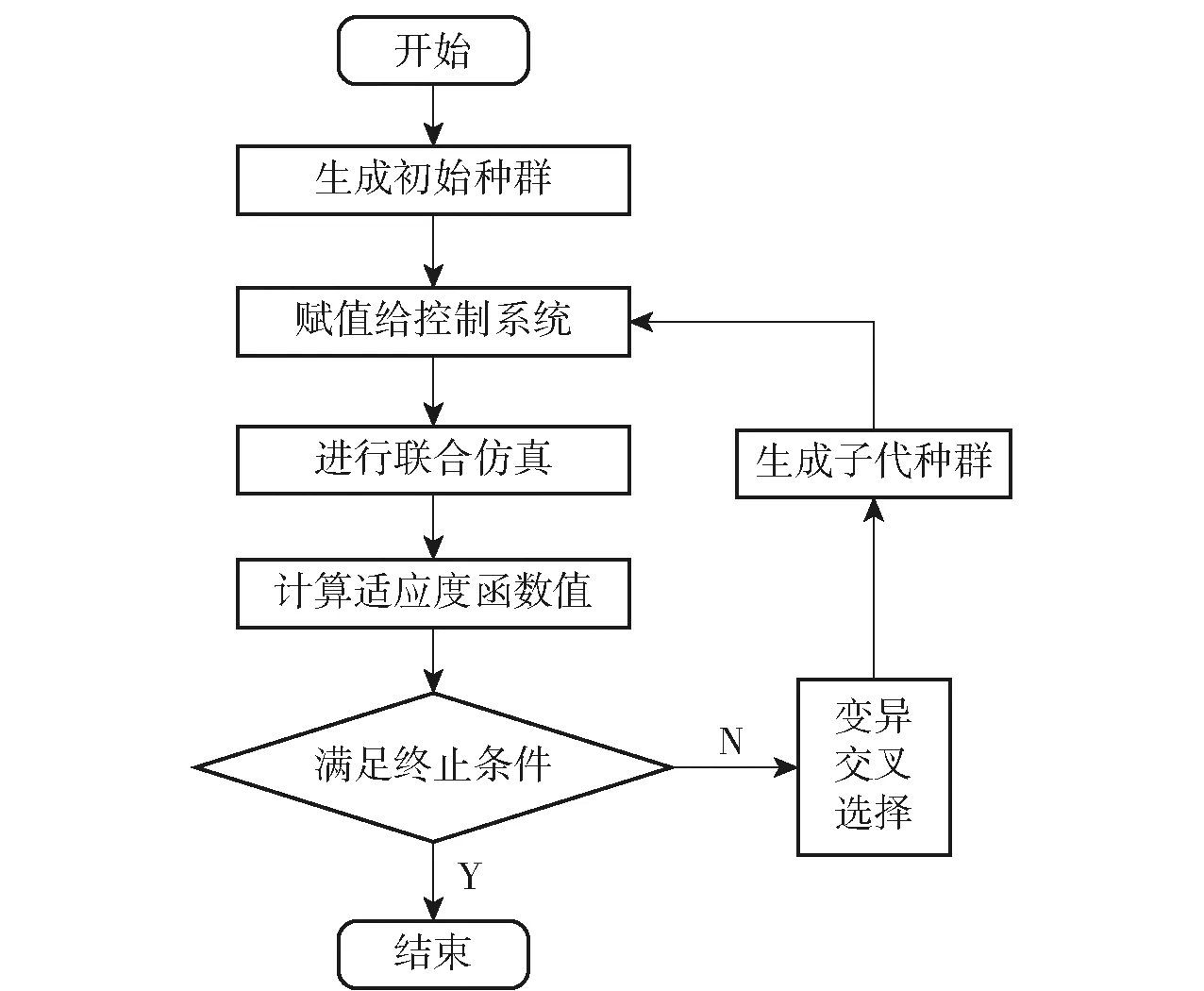
圖17 DE算法流程圖Fig.17 Flow chart of DE algorithm

2.3 仿真結果對比分析

為驗證DE算法整定PID參數的優越性，分別與原模型參數和遺傳算法(GA)整定的參數進行對比。DE算法基本參數選取：變異因子取0.4～1.2，交叉概率取0.3～0.9，初始種群取30，GA基本參數選取與DE算法一致。兩種算法目標函數值變化如圖18所示，從中可看出：經過20代迭代優化，DE算法整定得到高低隨動系統位置環PID參數kP、kI、kD分別為37.61、22.52、2.99，方向隨動系統位置環PID參數kP、kI、kD分別為12.30、0、0.05；GA整定得到高低隨動系統位置環PID參數kP、kI、kD分別為35.72、21.70、2.59，方向隨動系統位置環PID參數kP、kI、kD分別為13.27、0.25、0.06.

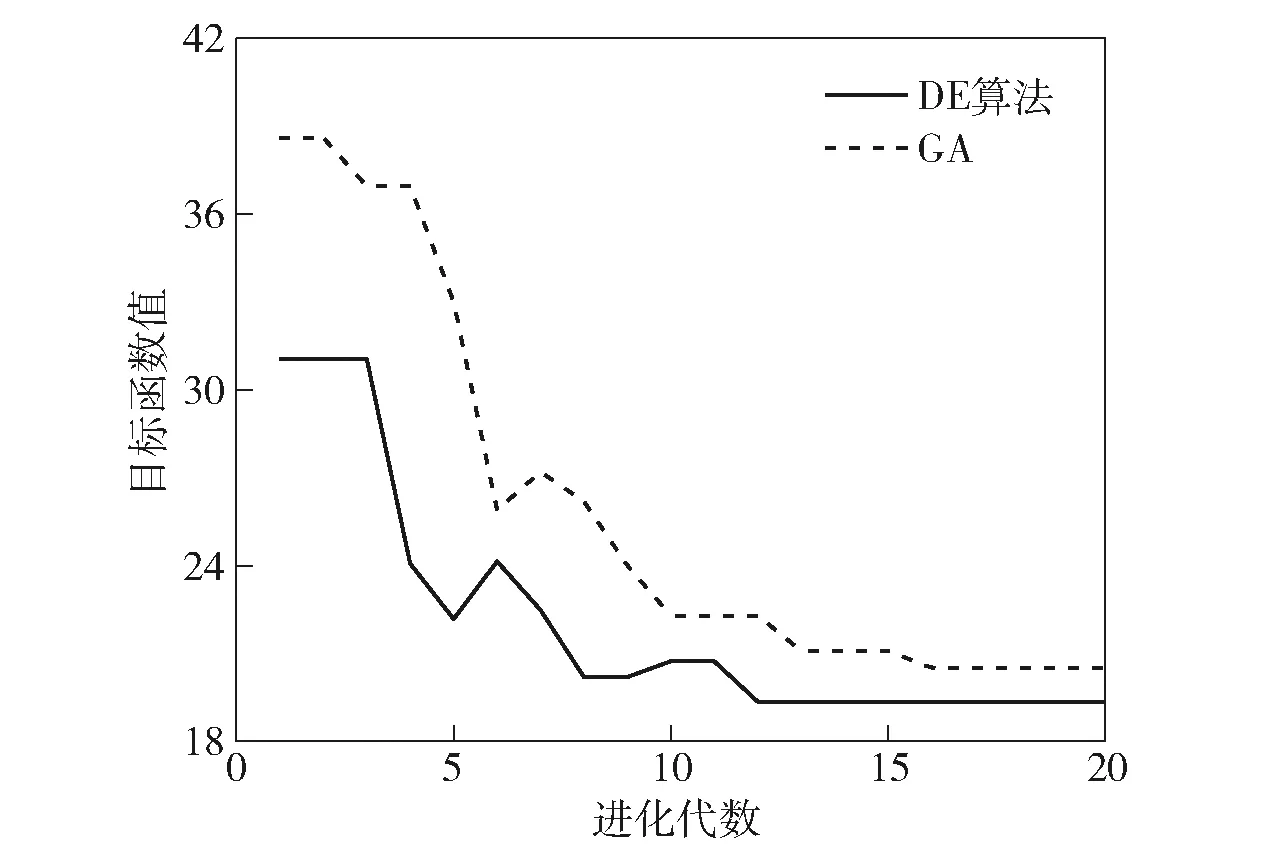
圖18 目標函數值Fig.18 Objective function value

對比分析時，將耳軸中心和目標點的連線與火力線之間的夾角作為調炮誤差，以分析火力線的控制精度及穩定性。優化前后仿真結果對比如圖19～圖21所示，數值對比如表2所示。

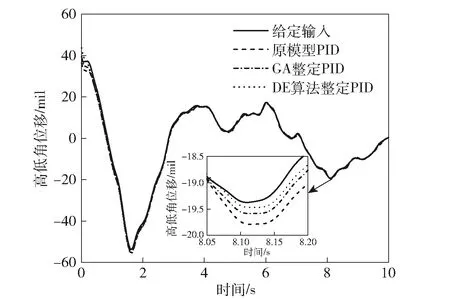
圖19 優化前后高低角位移Fig.19 Elevation angle displacements before and after optimization

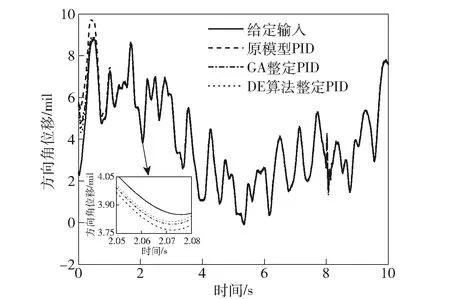
圖20 優化前后方向角位移Fig.20 Azimuth displacements before and after optimization

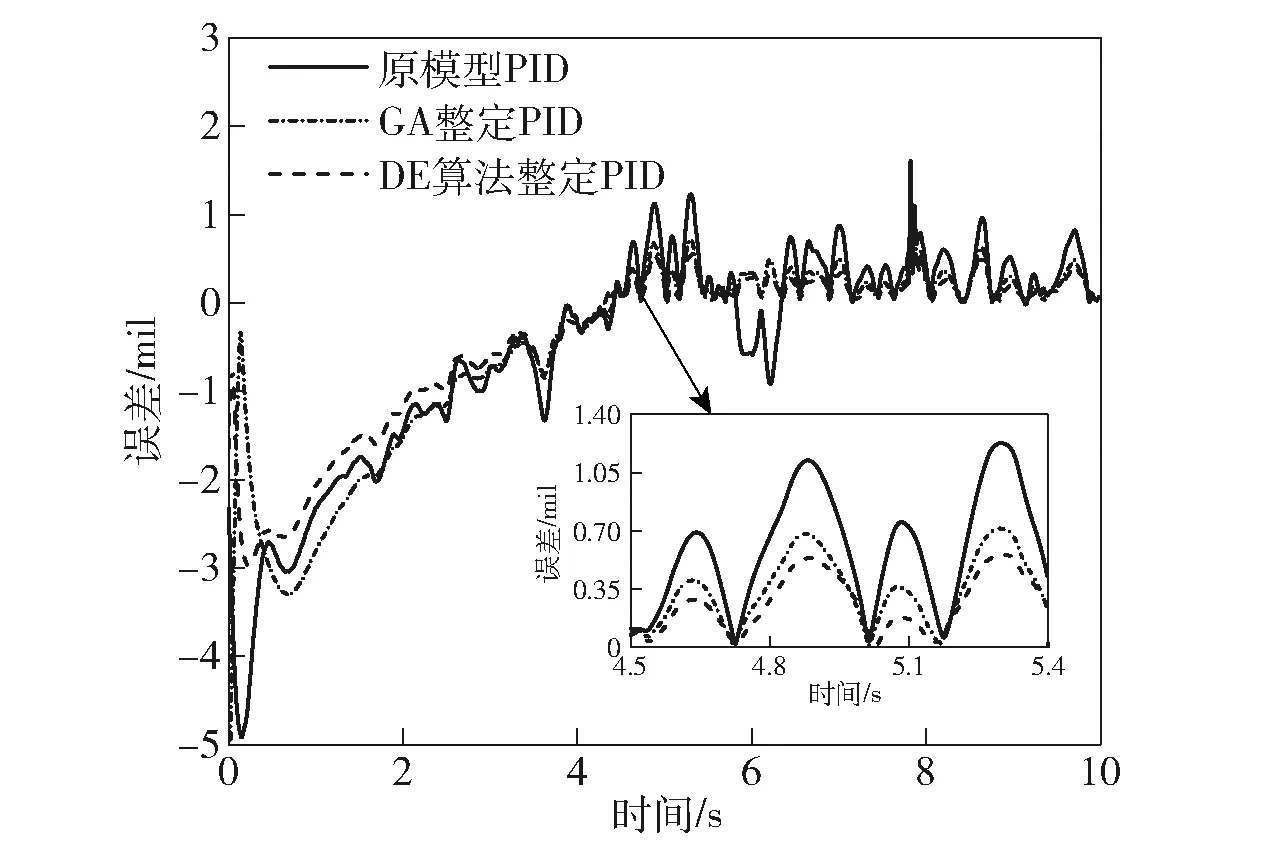
圖21 火力線控制誤差對比Fig.21 Comparison of control erorrs of firepower

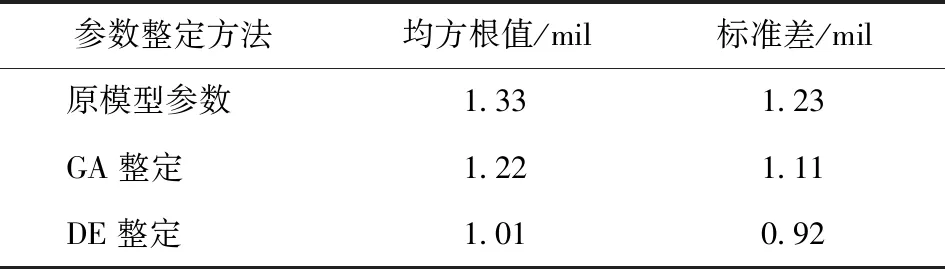
表2 優化前后火力線控制誤差對比Tab.2 Comparison of control errors of firepower before and after optimization

從圖19和圖20可以看到，在給定輸入信號速度和加速度變化較大的地方，DE算法整定的PID參數具有更好的跟蹤精度。從圖18、圖21和表2可以看到，與原模型中的PID參數相比，使用DE算法整定后的PID參數進行仿真，誤差的均方根值和標準差分別減少24.06%和25.20%，且能夠將誤差控制在3 mil內。相同條件下，與GA相比，DE算法收斂速度更快，且可以整定得到更優的控制參數。由此可見，使用該方法整定的PID控制參數可以進一步提高系統的穩態精度和動態性能。

3 結論

本文建立某高炮上裝動力學模型，考慮了各構件間的接觸碰撞、力元等因素。建立具有電流環、速度環和位置環三閉環結構的隨動控制系統，并針對被控對象具有較大轉動慣量這一特點，對位置環控制器采用了分區式PID控制方法。在此基礎上建立聯合仿真模型，通過DE算法整定了位置環小誤差區域的PID參數。由仿真分析結果，得到如下主要結論：

1) 基于聯合仿真模型得到的仿真數據與試驗數據相對誤差較小，且兩組數據相關系數均在0.9以上，說明所建立的聯合仿真模型有效可行，可用于高炮行進間火力線控制精度分析及PID控制參數優化。

2) 使用DE算法整定后的PID參數進行仿真，火力線控制誤差的均方根值和標準差分別減少24.06%和25.20%，說明DE算法整定得到的PID控制參數可進一步提高火力線的控制精度和穩定性。

本文對于進一步研究自行高炮行進間火力線控制精度及穩定性具有理論指導意義。

參考文獻(References)

[1] 謝潤,楊國來.自行高炮行進間射擊炮口響應特性研究[J].兵工學報,2014,35(8):1158-1163.

XIE R,YANG G L.Research on response characteristics of muzzle for self-propelled anti-aircraft gun firing on the move[J].Acta Armamentarii,2014,35(8):1158-1163.(in Chinese)

[2] 戴東明,毛保全,徐禮,等.某遙控武器站行進間射擊炮口振動特性研究[J].火炮發射與控制學報,2012,33(2):38-41.

DAI D M,MAO B Q,XU L,et al.Muzzle vibration characteristics of a remote control weapon station shooting on the move[J].Journal of Gun Launch &Control,2012,33(2):38-41.(in Chinese)

[3] 陳宇,楊國來,謝潤,等.某坦克行進間炮口振動優化與分析[J].彈道學報,2016,28(4):86-89.

CHEN Y,YANG G L,XIE R,et al.Optimization and analysis of muzzle vibration for tank firing on the move[J].Journal of Ballistics,2016,28(4):86-89.(in Chinese)

[4] 陳吉,葛建立,謝潤,等.某防御戰車行進間射擊炮口動態擾動特性研究[J].兵器裝備工程學報,2020,41(10):86-90.

CHEN J,GE J L,XIE R,et al.Research on muzzle disturbance of missile-gun integrated vehicle during firing on move[J].Journal of Ordnance Equipment Engineering,2020,41(10):86-90.(in Chinese)

[5] 劉昕運,馬吉勝,何健,等.某自行火炮行進間射擊建模與動態響應分析[J].火炮發射與控制學報,2016,37(3):6-10，16.

LIU X Y,MA J S,HE J,et al.Modeling and dynamic response of a self-propelled gun firing on the move[J].Journal of Gun Launch &Control,2016,37(3):6-10，16.(in Chinese)

[6] 宋雨荷,王軍,解軍,等.行進間射擊時路面譜作用下的高炮隨動誤差仿真分析[J].指揮控制與仿真,2020.[2020-07-02]http:kns.cnki.net/kcms/detail/32.1759.1628.004.html.

SONG Y H,WANG J,XIE J,et al.Simulation analysis of servo following error of antiaircraft gun under the effect of road spectrum in marching fire[J].Command Control &Simulation,2020.[2020-07-02]http:kns.cnki.net/kcms/detail/32.1759.1628.004.html.(in Chinese)

[7] 呂璐.行進間車載伺服系統控制策略及路譜算法研究[D].南京：南京理工大學,2017.

Lü L.Research on control strategy and road spectrum algorithm of vehicle mounted servo system[D].Nanjing:NanJing University of Science and Technology,2017.(in Chinese)

[8] 張雙運,蘇娟莉,王波,等.輪式自行高炮射擊線補償的一種途徑[J].火炮發射與控制學報,2009,31(4):1-3.

ZHANG S Y,SU J L,WANG B,et al.Fire line compension method of wheeled self-propelled AA gun system[J].Journal of Gun Launch &Control,2009,31(4):1-3.(in Chinese)

[9] 胡繼輝,侯遠龍,高強,等.坦克炮控系統神經網絡自適應滑模控制方法[J].火力與指揮控制,2018,43(6):118-121.

HU J H,HOU Y L,GAO Q,et al.Method of network adaptive sliding mode control of gun control system of tank[J].Fire Control &Command Control,2018,43(6):118-121.(in Chinese)

[10] 呂家兵,侯遠龍,高強,等.坦克炮控系統的復合自抗擾控制研究[J].自動化技術與應用,2020,39(4):1-7.

Lü J B,HOU Y L,GAO Q,et al.Research on composite active disturbance rejection control of tank gun servo system[J].Techniques of Automation and Applications,2020,39(4):1-7.(in Chinese)

[11] 尹達一,黃玉婷,劉云芳.基于MATLAB/Simulink的雙電機速度跟蹤伺服系統仿真[J].中國慣性技術學報,2011,19(2):229-233.

YIN D Y,HUANG Y T,LIU Y F.Simulation of double-motor speed tracking servo system based MATLAB/Simulink[J].Journal of Chinese Inertial Technology,2011,19(2):229-233.(in Chinese)

[12] 阮毅,楊影,陳伯時.電力拖動自動控制系統—運動控制系統[M].第5版.北京:機械工業出版社,2016:68-73.

RUAN Y,YANG Y,CHEN B S.Control systems of electric drives-motion control systems [M].5th ed.Beijing:China Machine Press,2016:68-73.(in Chinese)

[13] STORN R,PRICE K.Differential evolution - a simple and efficient heuristic for global optimization over continuous spaces[J].Journal of Global Optimization,1997,11(4):341-359.

[14] 劉金琨.先進PID控制MATLAB仿真[M].第4版.北京:電子工業出版社,2016:329-332.

LIU J K.Advanced PID control and MATLAB simulation[M].4th ed.Beijing:Publishing House of Electronics Industry,2016:329-332.(in Chinese)

[15] 譚飛,曹立佳.基于改進動態變異差分進化的最優PID控制[J].控制工程,2019,26(3):461-468.

TAN F,CAO L J.Optimal PID control based on the improved dynamic mutation differential evolution algorithm[J].Control Engineering of China,2019,26(3):461-468.(in Chinese)