渦旋管分離器結構參數對其性能影響的數值研究

湯浩，李麗，畢云棟，許立

(大連交通大學 機械工程學院，遼寧 大連 116028)*

渦旋管分離器由旋風分離器演化而來，又稱軸流旋風分離器，與傳統的旋風分離器相比，其體積小、安裝容易、成本與維修成本低.渦旋管分離器一般在分離微小顆粒的工作環境中使用，在分離過程中，氣流夾雜著固體小顆粒軸向進入渦旋管分離器，在旋流葉片處，固體顆粒在慣性力的作用下，沿著慣性旋流管，從灰塵口排出，其余的氣體經過集氣管，由集氣口流出，進行二次過濾或直接排放[1].

自1969年渦旋管分離器被兩家公司合作實驗研究并用于直升機的過濾裝置以來，國內外開始了對渦旋管分離器的研究，并將其應用到軍、工、醫學等領域，現在渦旋管分離器在直升機和燃氣輪機的進氣防護、煙草過濾、醫藥、生物等行業中都有應用.隨著研究流體力學軟件的日趨成熟與人們對過濾裝置的需求，渦旋管分離器的研究也被人們重視起來[2-3].楊漢杰等[4]對車載燃氣輪機的砂塵分離器進行數值模擬，建立了一套試驗系統與數值模擬的結構，通過數據對比得到渦旋管的設計方案，試驗結果基本達到進氣防護的要求.萬兵兵[5]通過氣液兩相流歐拉法對渦旋管分離器結冰情況進行數值模擬，并結合冰風洞試驗證明該方法正確有效.林秀麗等[6]研究了在不同的風速下，旋風分離器葉片間距,旋轉角度及排塵間隙對阻力和切向速度的影響，為軸流旋風分離器結構參數設計提供了依據.邱良燕[7]采用正交設計和響應曲面法對影響軸向旋流分離器性能的結構參數進行了探討，并通過試驗進行了驗證.

本文主要研究渦旋管分離器葉片角度、灰塵口大小、葉片后端軸長度、葉片軸直徑對分離效率與總壓損失的影響.

1 計算模型及模擬方法

1.1 計算模型

本文研究的渦旋管分離器，其幾何模型如圖1所示，主要由慣性旋流管、旋流葉片、集氣管組成.

使用ICEM軟件繪制渦旋管分離器計算域模型，這里采用四面體非結構化網格，網格數在45萬左右.

1.2 性能參數

分離效率η是衡量渦旋管分離器的最重要參數指標為：

(1)

總壓損失也是衡量渦旋管分離器的參數指標之一，總壓為靜壓和動壓之和.

Δp0=p01-p02

(2)

p0=p+(1/2)ρu2

(3)

式中：Δp0為總壓損失；p01為進口處總壓；p02為主流出口處總壓；p為靜壓；(1/2)ρu2為動壓；ρ為密度；u為速度.

在渦旋管分離器中的總壓損失較大的地方一般位于氣流碰撞到葉片處、旋流葉片流道內、橫截面積變化較大處.

1.3 模擬方法

流體流動遵循守恒定律，包括質量、能量和動量守恒定律[8].

質量守恒方程又稱連續方程，其方程為：

(4)

能量守恒方程為：

(5)

動量守恒方程在x、y、z三個方向為：

(6)

(7)

(8)

式中，t為時間；u為速度矢量；u、v、w為u在x、y、z方向的分量；T為時間；cp為比熱容；k為傳熱系數；ST為粘性耗散項；τxx、τxy、τxz是粘性應力τ的分量；FX、Fy、Fz是微元體的體力.

目前計算多相流有兩種方法，歐拉-拉格朗日方程和歐拉-歐拉方程.本文采用基于歐拉-拉格朗日方程的離散項(DPM)模型來計算多相流.在離散項(DPM)模型中，顆粒作為離散相，流體作為連續相，這里離散相占比小于10%，因此在計算過程中，不考慮粒子間的作用力，顆粒的運動軌跡都是獨立的[9].

顆粒沿X方向平衡方程為：

(8)

(9)

在平衡方程中：up為粒子速度；FD為粒子單位質量曳力；gx為X方向重力加速度；ρp為粒子密度；Fx為其他作用力；μ為流體粘性；CD為曳力系數；Re為相對雷諾系數；dp為粒子直徑大小.

1.4 初始條件和邊界條件設置

邊界條件主要設定為：工況環境為一個大氣壓，渦旋管分離器入口設置為壓力入口、逃逸(escape)邊界，空氣出口為壓力出口,表壓-500 Pa、逃逸(escape)邊界，灰塵口為壓力出口，表壓-500Pa、捕獲(trap)邊界.慣性旋流管壁面、旋流葉片、集氣管壁面均為反射(reflect)邊界.

顆粒相中，顆粒的直徑為10 μm，定義顆粒形狀為球形[1]，密度為1 550 kg/m3，設定顆粒均勻分布在壓力入口截面，該截面有3 553個網格，假設從同個網格進入的顆粒運動軌跡一樣，假設質量流量為5×10-8kg/s，共模擬了1.7×105個真實粒子的軌跡.

1.5 仿真工況設定

在四個結構參數組合的工況中，通過每次只改變參數中的一個，可以得出每個參數對分離效率和總壓損失的影響，仿真模擬的各工況如表1所示.

表1 仿真結構參數表

2 數值模擬結果分析

2.1 葉片旋轉角度對性能的影響

比較第Ⅰ組中試驗號為1、2、3的數據，通過數值模擬得出葉片旋轉角度對總壓損失與分離效率的影響，如圖2所示.從圖中看出旋流葉片的旋轉角度由160°增大到180°，總壓損失逐漸增大，分離效率也逐漸增大，當葉片角度為180°時，總壓損失達到125.27 Pa.這是由于葉片旋轉角度增大時，渦旋管內葉片處的氣流流過的通道彎曲程度增大，使氣流與葉片的碰撞作用力也隨之增大，導致了較大的總壓損失.

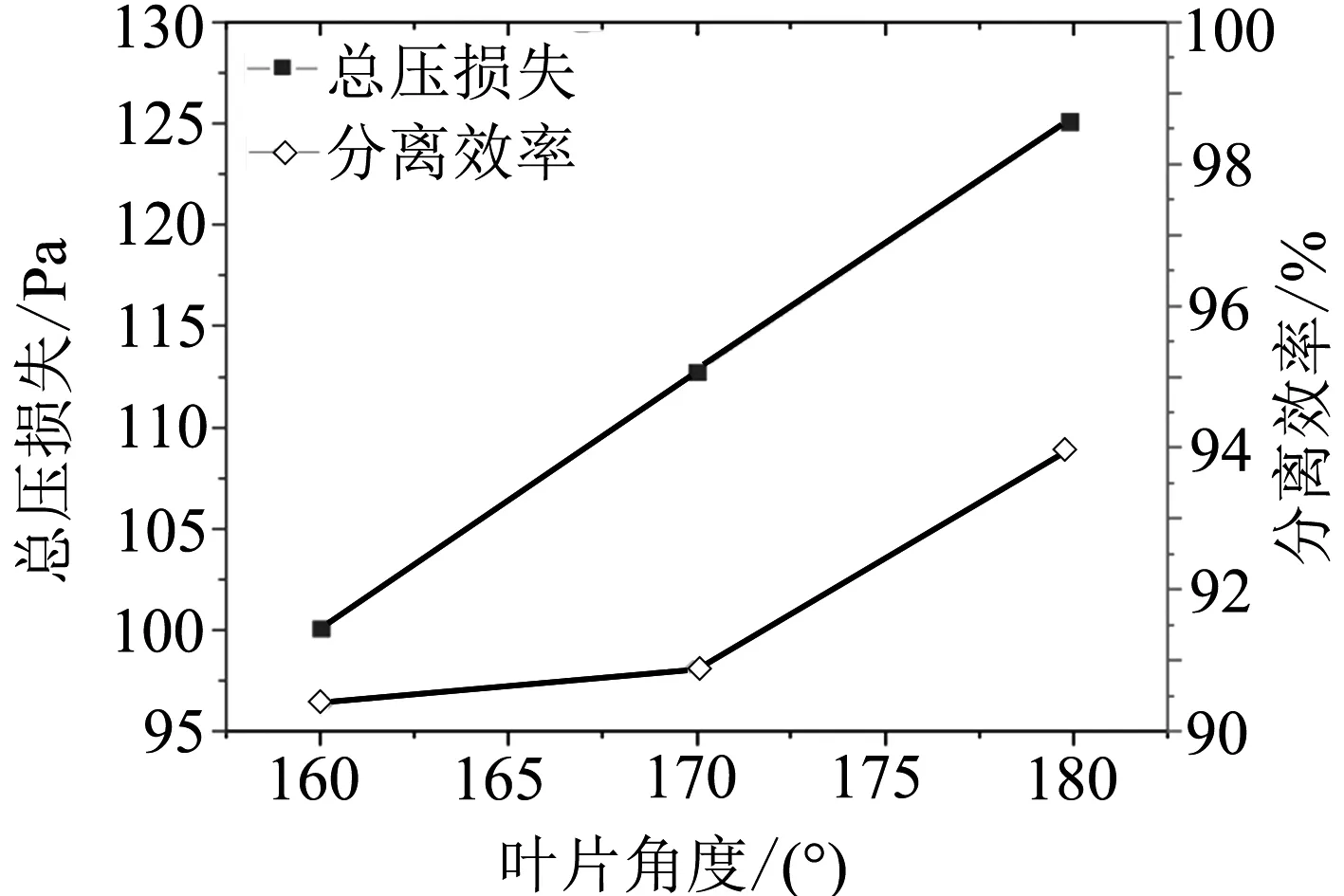
圖2 三種葉片角度的總壓損失與分離效率

2.2 灰塵口大小對性能的影響

比較第Ⅱ組中試驗號為4、5、6的數據，通過數值模擬得出灰塵口大小對分離效率和總壓損失的影響，如圖3所示.從圖中看出灰塵口由1.5mm增大到2.5 mm，總壓損失逐漸增大，分離效率逐漸增大，變化率達到了6%，同時，總壓損失達到了188.76Pa.這是由于灰塵口變大，通過灰塵口的流量增大，則通過集氣口的流量變小，速度變小，從而動壓變小，同時集氣口靜壓不變，則集氣口總壓p02變小.在分離器入口總壓p01不變的情況下，則總壓損失Δp0增大.并且由于灰塵口增大，捕獲的粒子數量增加，從而分離效率增大.

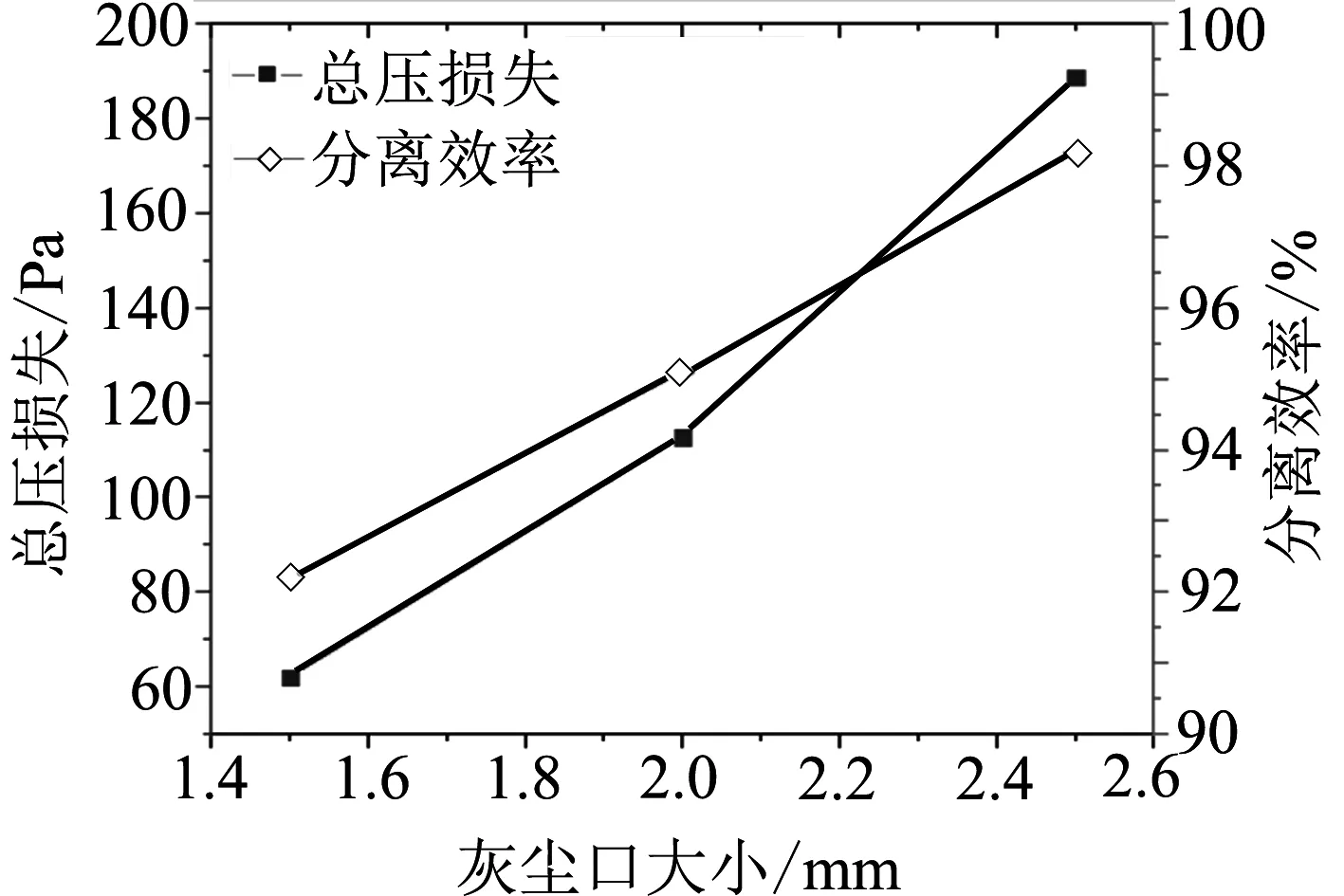
圖3 三種灰塵口大小的總壓損失與分離效率

2.3 葉片后端軸長對性能的影響

比較第Ⅲ組中試驗號為7、8、9的數據，通過數值模擬得出葉片后端軸長對分離效率和總壓損失的影響，如圖4所示.從圖中可以看出葉片后端軸長度增大，總壓損失增長較小，從103.62Pa增大到107.46 Pa，分離效率先增大至97.1%后減小至95.2%.這是因為葉片后端軸長度影響了粒子在軸末端到灰塵口的運動軌跡，適當的長度有利于粒子向灰塵口移動，提高分離效率.總壓損失略微增大，是因為葉片軸變長，增加了一定的沿程損失.

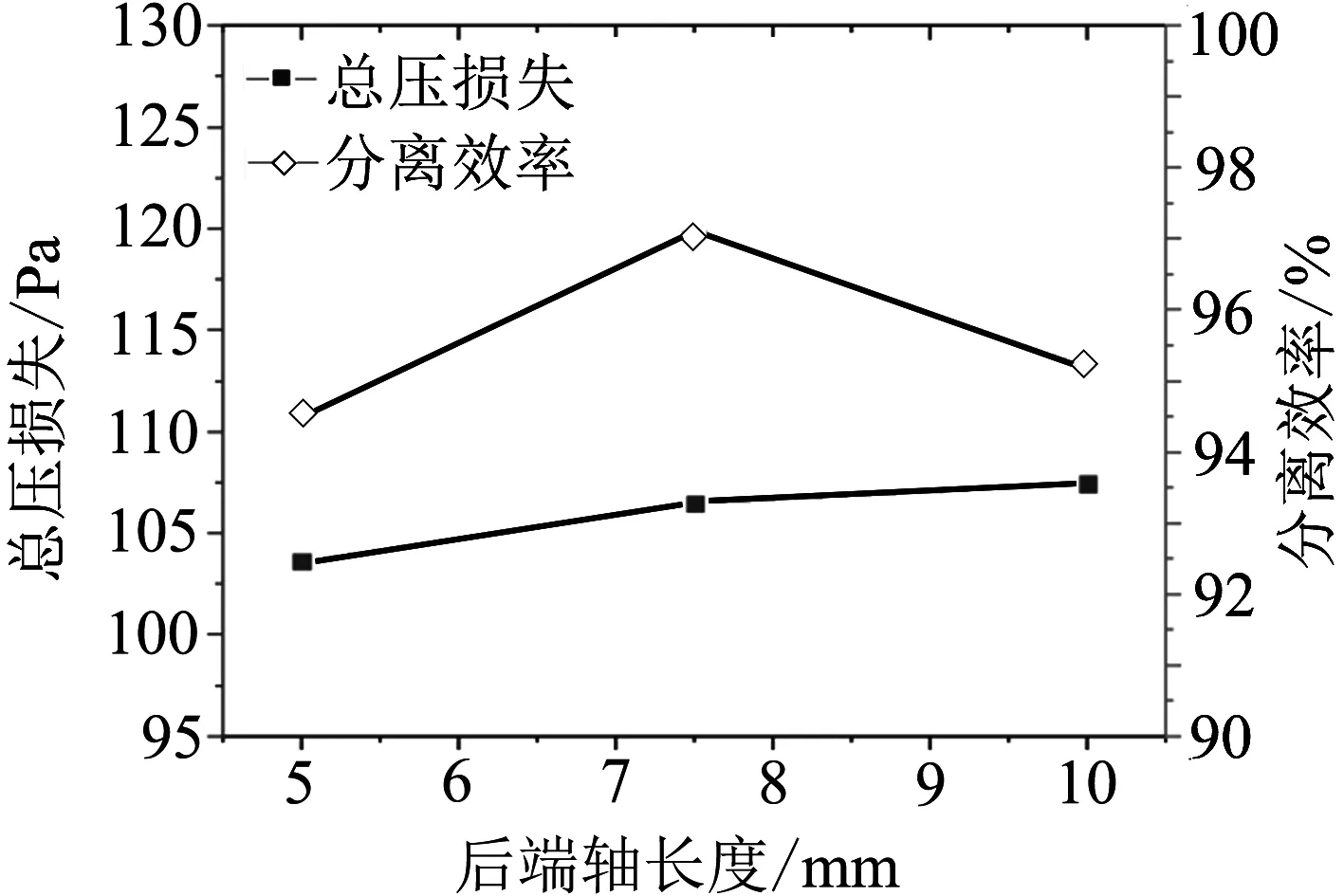
圖4 三種后端軸長度的總壓損失與分離效率

2.4 葉片軸直徑對性能的影響

比較第Ⅳ組中試驗號為10、11、12的數據，通過數值模擬得出葉片軸直徑對分離效率和總壓損失的影響，如圖5所示.從圖中可以看出葉片軸直徑由3 mm增大到4 mm，總壓損失增大2.71 Pa，分離效率先由94.4%增大至95.1%后幾乎不變，這說明葉片軸直徑的大小對渦旋管分離器的性能影響較小.

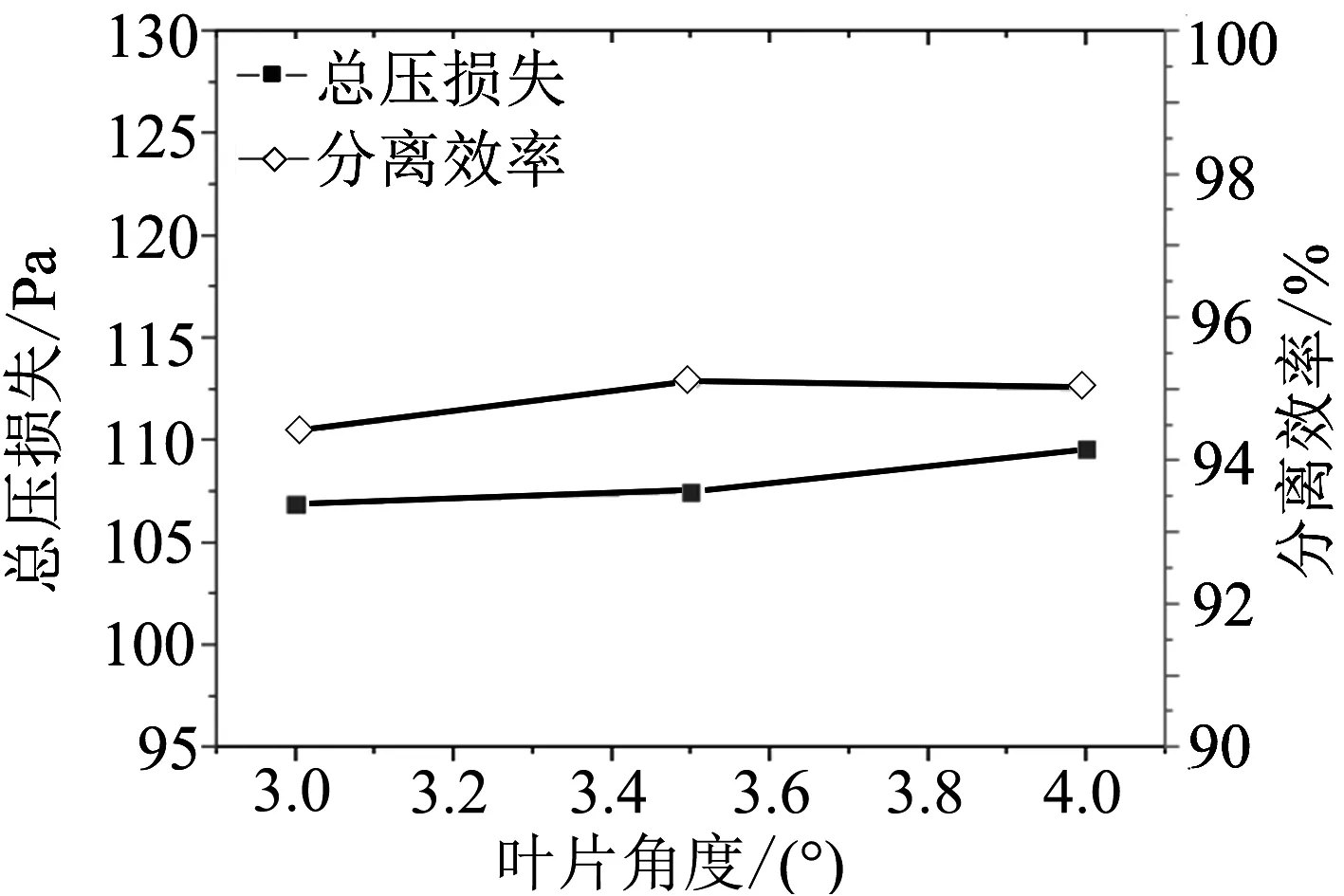
圖5 三種葉片軸直徑的總壓損失與分離效率

2.5 模擬結果分析

以試驗號6為例，從模擬結果中可以得知，灰塵口的大小對分離效率和總壓損失的影響是最大的，當灰塵口的大小為2.5 mm時，其分離效率達到了98.2%，但是總壓損失也是最大的，達到了188.76 Pa，這說明增大灰塵口提高了分離效率，但也增加了總壓損失.

渦旋管分離器內流域速度矢量分布如圖6所示.由圖中可以看出速度較大的地方分布在靠近旋流葉片、灰塵口和集塵口處.靠近旋流葉片處的速度較大是葉片使氣流受到離心力，從而速度增加，灰塵口和集氣口處速度較大是由于出口通流截面積較小.

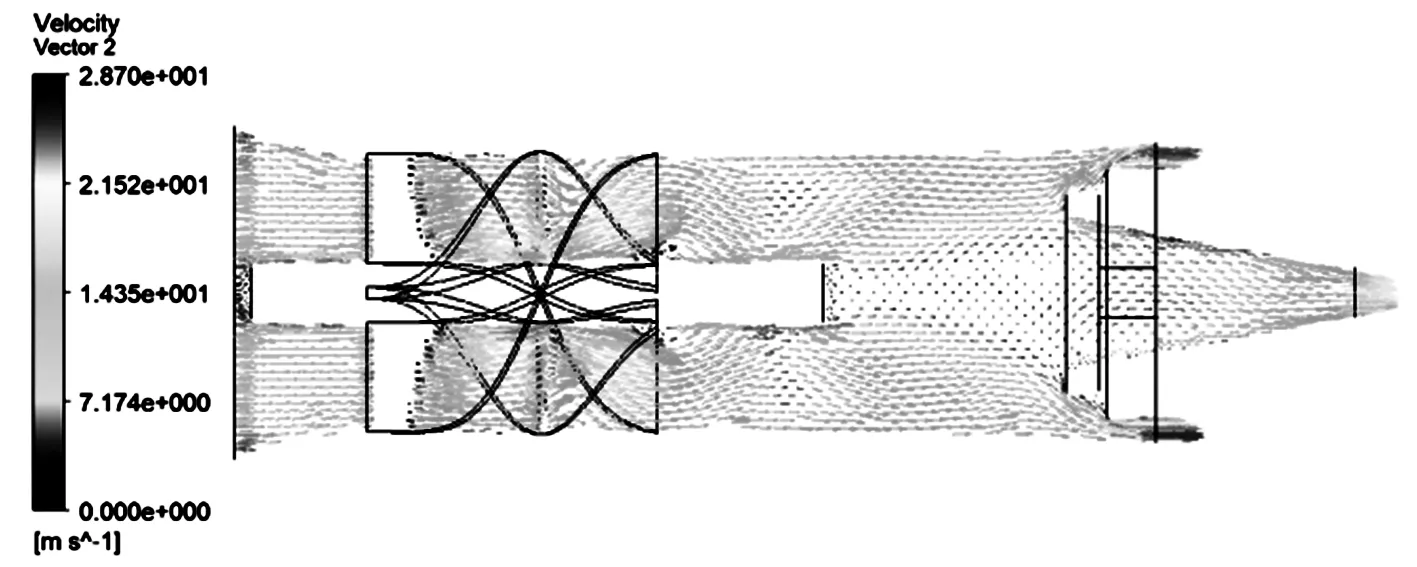
圖6 速度矢量分布云圖

顆粒路徑圖能夠更直觀的觀察粒子在渦旋管分離器中的運動路徑，如圖7所示.從圖中可以看出，粒子從入口進入，與螺旋葉片發生碰撞，并在離心力的作用下，貼在慣性旋流管的內壁向出口運動，粒子大部分從灰塵口排出，極少數從集氣口逃逸.

圖7 粒子路徑圖

3 結論

本文以渦旋管分離器為模型，結合數值模擬分析方法，分別改變渦旋管分離器的葉片角度、灰塵口大小、葉片后端軸長度和葉片軸直徑，得到渦旋管分離器結構參數對總壓損失與分離效率的影響.

數值模擬結果表明，旋流葉片的旋轉角度增大20°，總壓損失由100.09 Pa增大到125.27 Pa，分離效率由90.4%增大到94%；灰塵口增大1mm，總壓損失由62.05 Pa增大到188.76 Pa，分離效率由92.2%增大到98.2%；葉片后端軸長度增大5 mm，總壓損失由103.62Pa增大到107.46Pa，分離效率先由94.5%增大至97.1%后減小至95.2%；葉片軸的直徑增大1 mm，總壓損失由106.87 Pa增大到109.58 Pa，分離效率由94.4%增大至95.1%后變化很小.其中，灰塵口大小對總壓損失和分離效率的影響較大，葉片旋轉角度、葉片后端軸長、葉片軸的直徑增大對總壓損失和分離效率的影響較小.

本文只對渦旋管分離器的部分結構參數做出數值分析，今后還可以對工作環境等參數做出研究.