面向纖維單元的鋼筋混凝土材料滯回本構模型開發
劉軍,趙晶, 王德斌, 張吉松
(大連交通大學 土木工程學院,遼寧 大連 116028)*
當前,大量復雜的鋼筋混凝土結構修建在地震活動特別是“大震”頻發的高烈度區.因此,保證復雜結構具有良好的抗震性能是工程抗震領域研究的重點問題.為此,近些年基于性能的抗震設計方法[1]得到了發展.該方法需要對工程結構進行非線性的彈塑性分析.此外,對既有結構進行抗震性能評估和抗震加固設計同樣需要以其地震非線性響應作為依據.在眾多的地震非線性分析模型中,纖維模型由于能適用于任何截面形式的構件能夠直接考慮軸力和彎矩的耦合作用,可模擬不同類型鋼筋和混凝土材料,只需要其單軸本構關系、兼顧計算精度和計算效率兩方面考慮等優點,得到了廣泛應用[2].因此,開發面向纖維單元的鋼筋和混凝土材料滯回本構模型具有實際工程意義.
本文在考慮骨架曲線、滯回規則、損傷特性、箍筋約束效應及壓-拉轉換的剛度退化特性的基礎上,建立混凝土和鋼筋單軸滯回本構模型.利用FORTRAN語言開發本構模型的隱式算法子程序.以NSCP(Nonlinear Seismic Calculation Program)程序為平臺,通過材料子程序接口,實現所開發的材料模型與主程序間的數據傳遞.在材料及結構層次上分別進行數值模擬,其結果與試驗結果進行對比,驗證本文所建立的材料模型和開發的子程序在工程結構地震非線性分析方面具有適用性和有效性.
1 混凝土滯回本構模型
1.1 骨架曲線
(1)壓縮骨架曲線
Hoshikuma[3]根據圓形和矩形截面的鋼筋混凝土柱試件受壓試驗結果,在Kent-Park模型的基礎上建立了考慮約束效應的混凝土應力-應變模型.由于該模型表達簡單、參數少,計算效率高,因此用于本文研究.其骨架曲線的表達式見式(1).
(1)
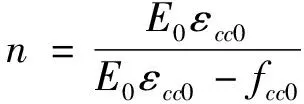
(2)
(3)
fcc0=fc0+3.8αρsfyh
(4)
εcc0=0.002+0.033βρsfyh/fc0
(5)
εccu=εc0+0.8fcc0/Edes
(6)
式中:E0、Edes、fcc0、εcc0和εccu的物理意義見圖1(a);fc0為素混凝土的抗壓強度;ρs為箍筋的體積配箍率;fyh為箍筋的屈服強度.對于圓形截面,α=1.0,β=1.0;對于矩形截面α=0.2,β=0.4.fc0、εc0為非約束混凝土的的峰值應力和對應的應變.非約束混凝土受壓骨架曲線方程,見文獻[3].
(2)拉伸骨架曲線
混凝土拉伸骨架曲線上升段采用直線,下降段采用冪函數形式.其表達式為:
(7)
式中:εt0、ft0的物理意義見圖1(b);n′為拉伸軟化指數,控制軟化剛度,依據文獻[4]建議取0.85.
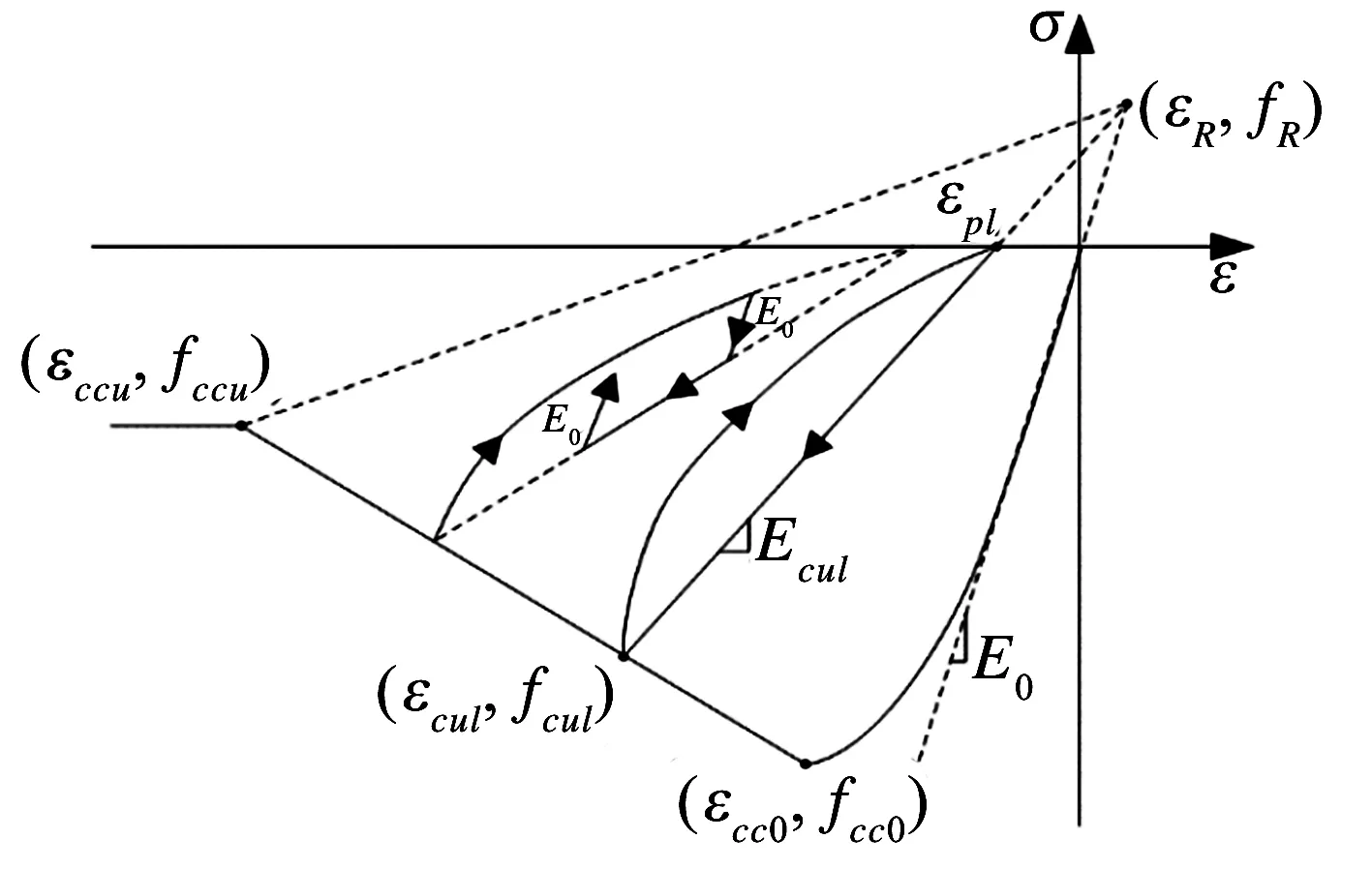
(a)壓縮
1.2 滯回規則
(1)壓縮滯回規則
混凝土受壓完全卸載后再加載規律依據Yassin[5]提出的“交點法”得到.從骨架曲線上完全卸載后再加載路徑反向均相交于R點.如圖1(a),根據幾何關系,R點的坐標為:
(8)
式中,Eu為點(εcul,fcul)處的再加載模量,需要根據試驗結果事先確定.
骨架曲線上的卸載點(εcul,fcul)與R點的連線交于應變軸處的應變即為塑性應變εpl,完全卸載的路徑為過卸載點(εcul,fcul)和(εpl,0)兩點的一條曲線.為了建立完全卸載方程,在如圖2所示的曲邊ΔABC中,應力變化相對應變變化存在非線性比例關系,該關系可以表示成:
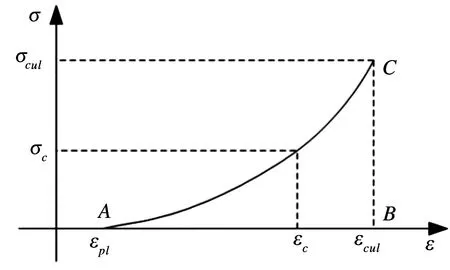
圖2 受壓完全卸載曲線
(9)
其中,γ為非線性比例因子.
考慮卸載開始時的卸載剛度不能超過初始加載剛度E0,且該曲線形狀是凸向應變軸,因此:
(10)
部分卸載路徑仍然沿著骨架曲線上對應的卸載點處完全卸載路徑進行,而部分卸載再加載時沿著剛度為E0的直線到達完全卸載后再加載直線路徑時,繼續沿該直線加載,在未到達骨架曲線前卸載時,繼續沿剛度為E0的直線到達完全卸載曲線路徑時,再繼續沿該曲線卸載,如此反復.
(2)拉伸滯回規則
考慮到拉伸重復加卸載產生的不可恢復變形和滯回耗能較小,本文拉伸卸載不考慮塑性應變,按返回原點的直線路徑卸載和再加載,如圖1(b).
1.3 損傷特性
為了描述混凝土的損傷特性,考慮拉壓不等性,分別建立了拉伸和壓縮損傷變量.
dt=1-Etul/E0
(11)
dc=1-Ecul/E0
(12)
式中:dt為拉伸損傷變量;dc為壓縮損傷變量;Etul和Ecul的物理意義見圖1.需要說明:①拉伸損傷只考慮彈性損傷,不計拉伸塑性的影響;而壓縮損傷為塑性損傷;②在部分加卸載過程中,保持以對應骨架曲線上卸載點計算的損傷值不變.
1.4 壓縮-拉伸轉換剛度退化
由壓縮卸載到反向拉伸加載時,拉伸再加載骨架曲線采用“平移法”獲得,如圖1(b)所示.考慮到壓縮過程的累計損傷對拉伸剛度的影響[6],其拉伸再加載剛度可以定義成:
Et=(1-ωdc)(1-dt)E0
(13)
式中,ω為拉伸剛度退化參數,表征壓縮累計損傷對拉伸損傷的影響,本文取0.2.
2 鋼筋滯回本構模型
縱向鋼筋應力-應變滯回關系采用Menegotto-Pinto模型[7],滯回關系見圖3.不考慮等向硬化,該模型的數學方程表達成:
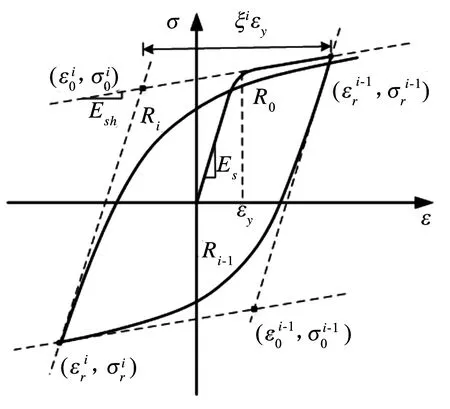
圖3 鋼筋滯回曲線
(14)
式中,b為屈服后鋼筋彈性模量與初始彈性模量之比,即b=Esh/Es.
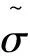
(15)

Ri為描述Bauschinger效應的參數,定義成:
(16)
其中:R0是Ri的初值,α1和α2為試驗常數.
(17)
(18)
3 材料模型子程序開發
針對本文建立的材料模型,采用FORTRAN語言編寫隱式算法的子程序.基于NSCP程序平臺,通過材料子程序接口,實現子程序與主程序間的數據交換.給定當前應變增量,主程序通過UMAT接口進入材料子程序,在當前積分點上計算該增量步的雅可比矩陣,從而更新當前應力,并記錄相應狀態變量,通過材料子程序接口返回主程序.子程序開發的流程如圖4所示.
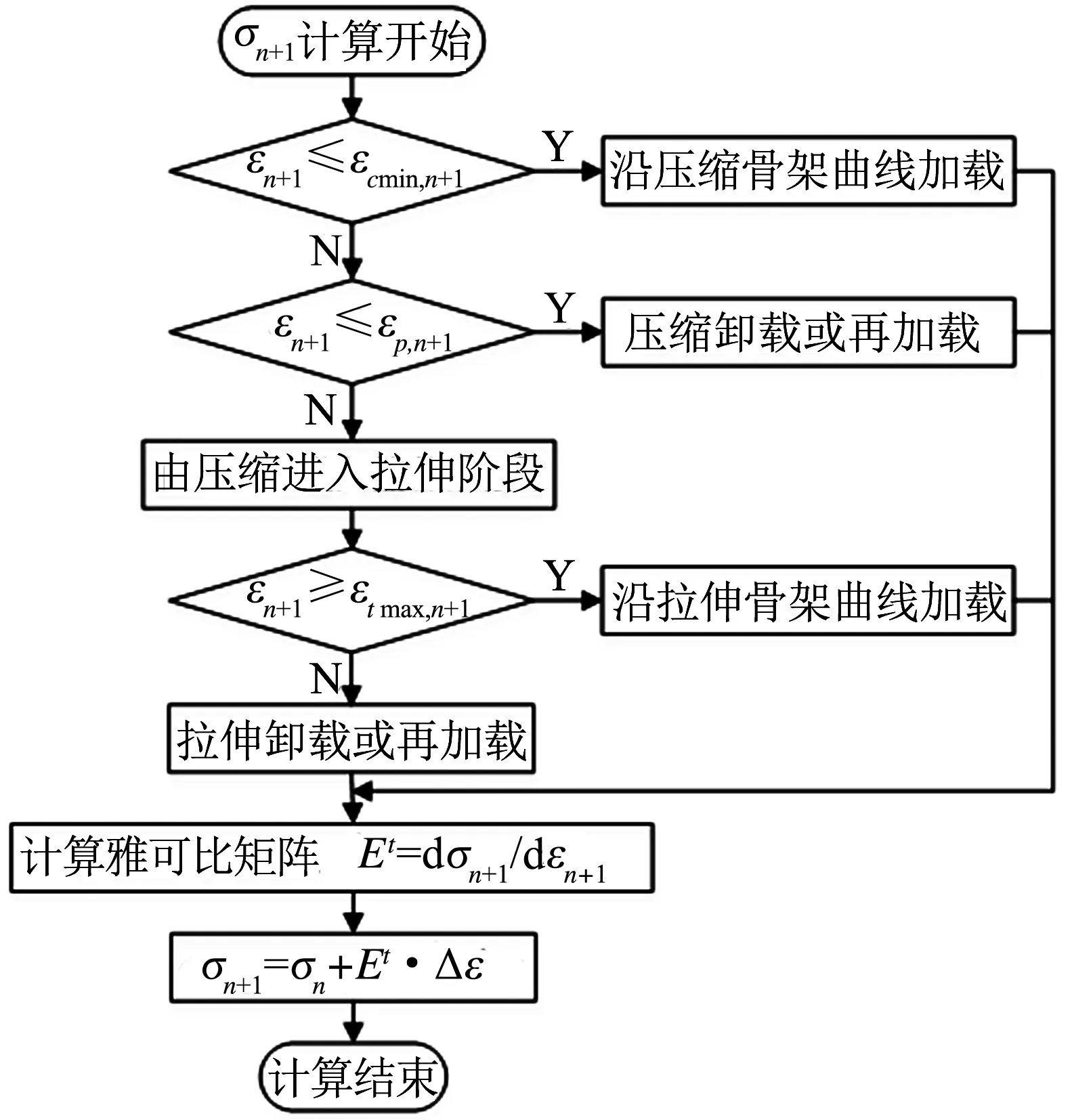
(a)混凝土
4 有限元模型的建立
本文采用課題組自編的NSCP 軟件進行數值模擬.單元類型選用程序提供的三維纖維梁單元.在構件長度方向布置若干節點,將構件劃分成若干個單元,保證單元長度與塑性鉸長度相一致.每個單元具有兩個節點,中間具有一個積分點,將積分點所在截面的混凝土材料劃分若干纖維,其中保護層纖維采用無約束混凝土的本構模型,核心區域纖維采用箍筋約束混凝土本構模型,鋼筋纖維采用Menegotto-Pinto本構模型.下文算例中,模型建立沒有包括混凝土基礎,墩(柱)根采用固定約束,以位移方式控制加載.
5 子程序驗證及應用
5.1 鋼筋和混凝土材料模擬
為了驗證材料模型程序的準確性,建立1 m長的方柱,截面尺寸為0.1 m×0.1 m.分別賦予混凝土和鋼筋的材料屬性,材料參數列于表1中.本節計算中未加說明的,長度單位為mm,強度單位為MPa,彈性模量單位為GPa,下同.測試混凝土材料時先拉伸加載后卸載,再非等幅重復壓縮加載,加載制度見圖5(a);測試鋼筋時采用幅值逐漸增大的往復位移加載方式,見圖5(b).

表1 材料參數
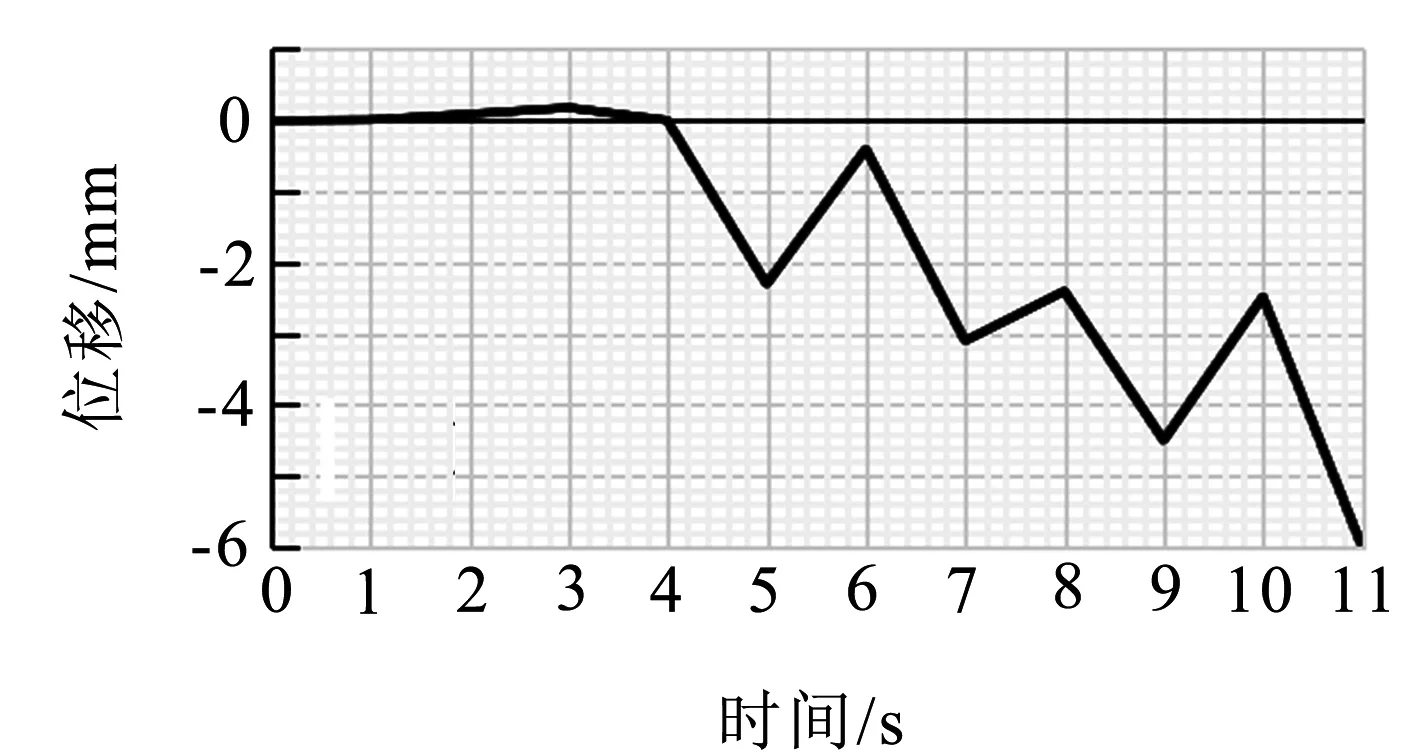
(a)混凝土
采用本文建立的材料模型和開發的子程序進行數值模擬,獲得的積分點處混凝土材料和鋼筋應力-應變關系曲線,如圖6所示.模擬結果顯示與混凝土理論本構模型目標骨架曲線、加卸載滯回曲線、拉壓不等性及剛度退化特性相一致.鋼筋的滯回特性和Bauschinger效應也得到了有效模擬.
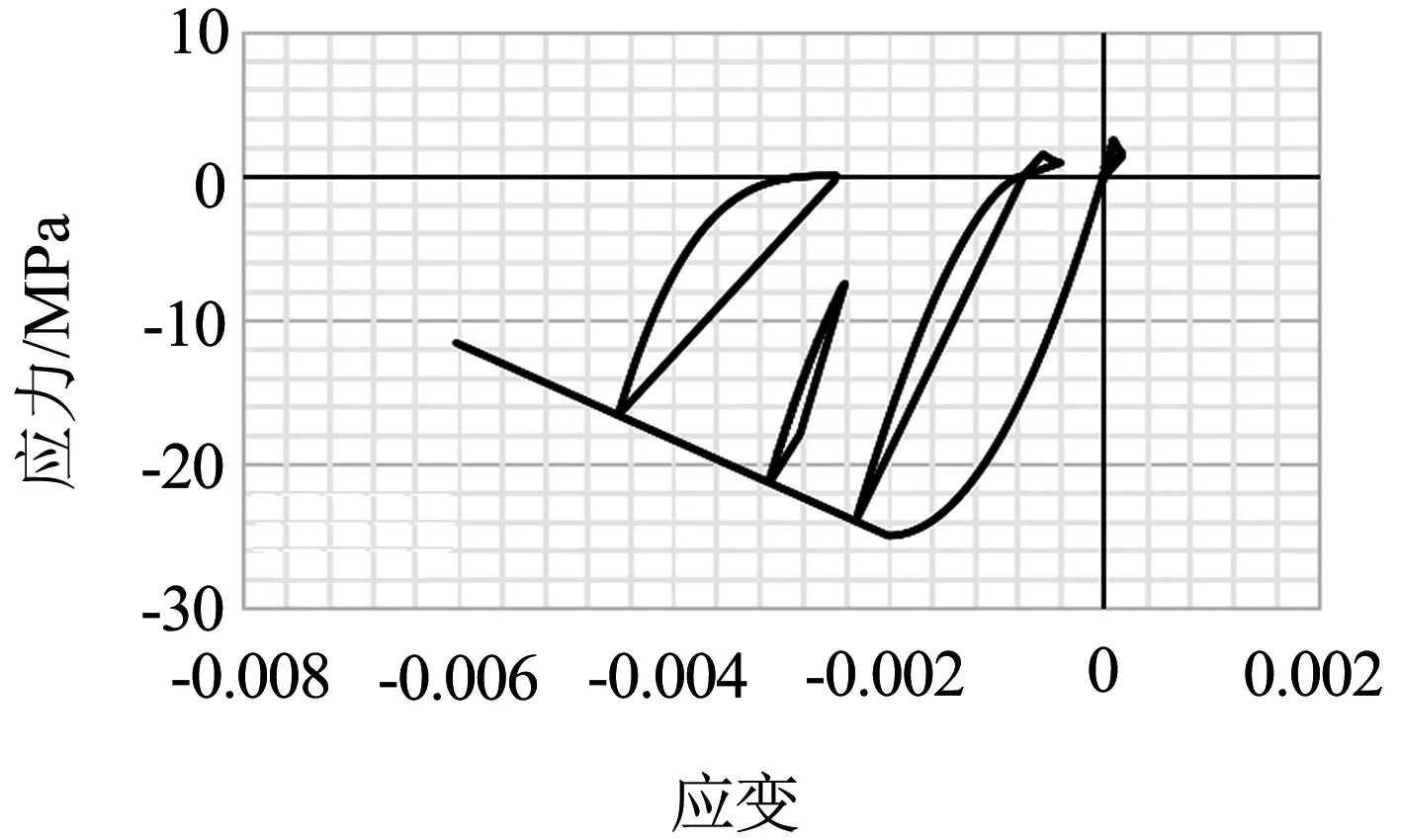
(a)混凝土
5.2 鋼筋混凝土橋墩動力時程加載試驗模擬
2010年,PEER和NEES發起了一個鋼筋混凝土橋梁墩柱的“盲預測競賽”[8],該墩柱在加州大學圣地亞哥分校NEES-UCSD振動臺上進行了一組6條地震動的動力單向激勵加載試驗.對6次地震動進行串聯分析,以便保證結構在前一次試驗中產生的損傷(通常是強度和剛度退化)進入下一次試驗分析中.試驗墩的幾何尺寸、縱向和橫向配筋情況見圖7.橋墩的材料參數見表2.
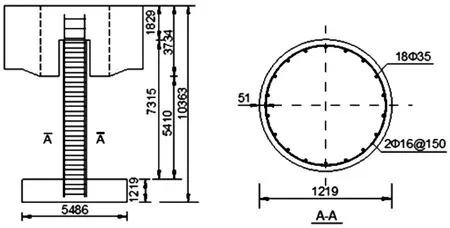
圖7 橋墩的幾何尺寸及配筋圖(單位:mm)

表2 橋墩的材料參數
軸向加載為2 535 kN,柱頂質量塊的轉動慣性矩為9 735 kN·m2/g,軸壓比為5.3%,縱向配筋率為1.55%,體積配箍率為0.95%.有限元建模中將橋墩均勻劃分為10個 單元.采用質量比例阻尼,第一模態對應的阻尼比取2%.將記錄的地震動運用Butterworth 濾波器進行濾波處理后作為地震動輸入用于數值分析.試 驗 結 果 顯示EQ3作用下鋼筋已經發生屈服,按照文獻[9]的考慮,本模擬只分析了EQ1~EQ3地震動,并取三組地震動的前60、80、60 s加以分析, 地震動加速度時程圖8所示,三次地震動最大加速度分別為14.55、38.99和80.95 cm/s2.數值模擬得到橋墩的動力時程響應見圖9.試驗結果表明,EQ1地震作用下最大位移62 mm,EQ3地震作用下最大位移361 mm,在非線性響應中,產生了-0.87%的殘余位移角或者-63 mm的殘余位移.模擬結果顯示,EQ1地震作用下最大位移為65 mm,EQ3地震作用下最大位移為373 mm,殘余位移角為-0.92%,殘余位移為-70 mm,誤差均較小.數值結果還表明,前兩次地震作用時,柱體基本保持彈性,第三次地震作用時,柱體進入塑性區,最大曲率與屈服曲率之比在4以上.橋墩現場試驗顯示,EQ3作用下橋墩已經發生了屈服,結構的損傷較明顯,有明顯的應變滲透現象,基礎頂部的墩柱縱向鋼筋出現了明顯的粘結滑移.由于本文建立的材料模型沒有考慮鋼筋和混凝土間的粘結滑移特性,故可能成為導致數值模擬和實驗結果間存在差異的主要原因.但從橋墩地震時程響應的波形和響應發生的時間等整體角度衡量,數值模擬和試驗結果吻合的較好.
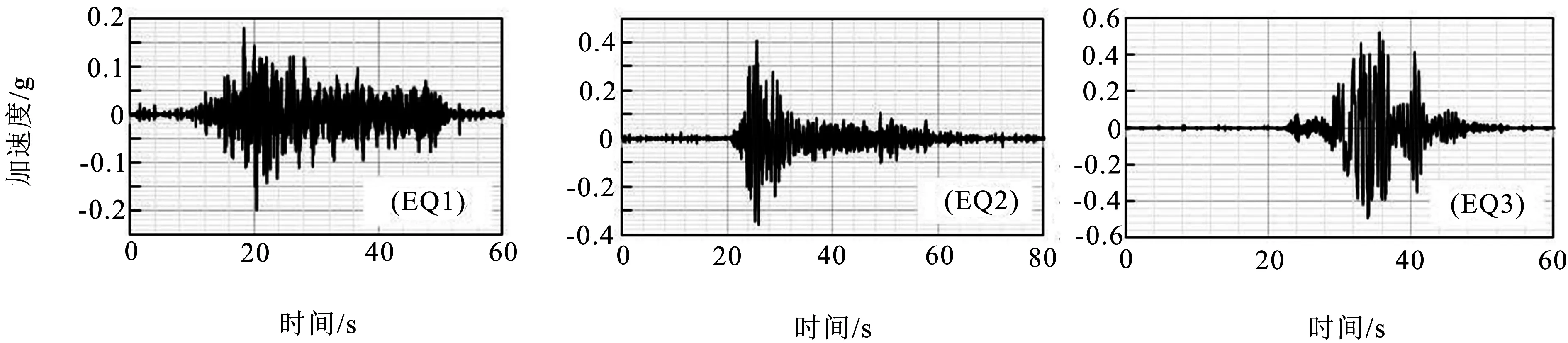
圖8 地震動加速度時程
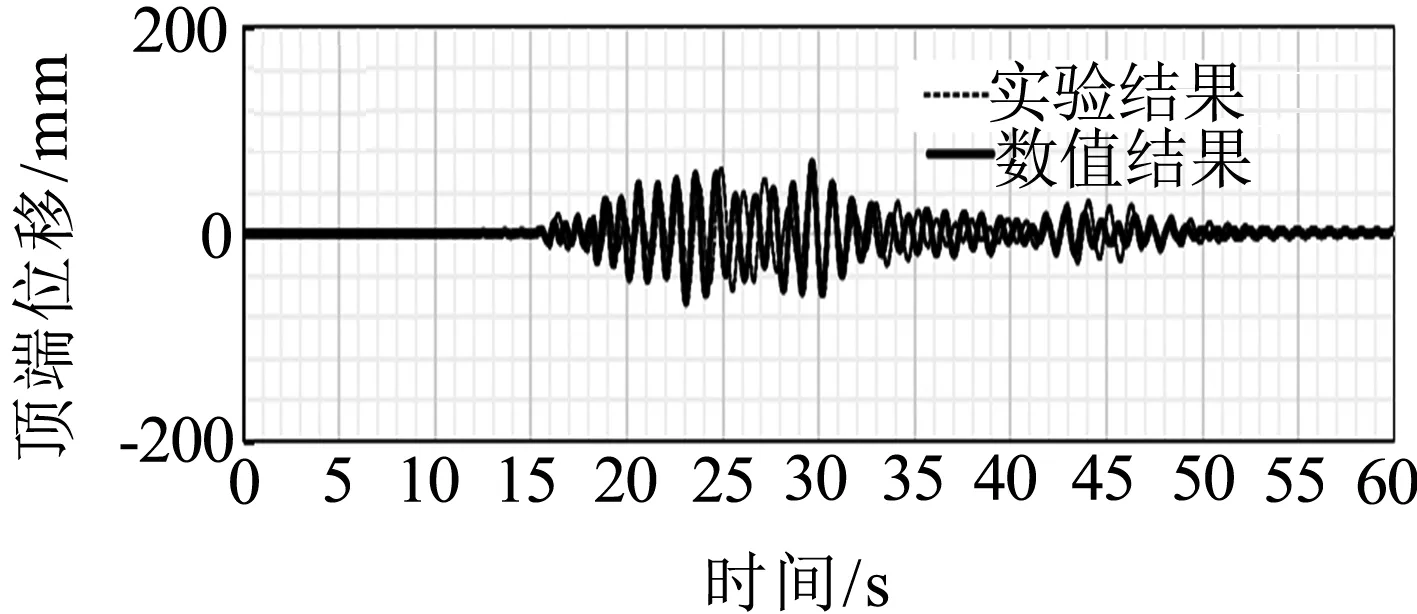
(a)EQ1
6 結論
本文考慮骨架曲線、滯回規則、損傷特性、箍筋約束效應及壓-拉轉換的剛度退化特性等,建立了混凝土單軸滯回本構模型.鋼筋采用經典的Menegotto-Pinto模型.開發了隱式算法的材料本構子程序.以NSCP計算程序為平臺,通過材料子程序接口,實現所開發的材料模型子程序與主程序間的數據傳遞.采用纖維模型,對鋼筋和混凝土兩種材料及橋墩結構分別進行數值模擬分析,其結果與試驗結果進行對比,表明兩者在最大承載力、卸載剛度、時程響應等整體結果上吻合較好,具有可靠的計算精度,驗證了本文所建立的材料理論本構模型和開發的子程序,在工程結構地震非線性分析方面具有適用性和有效性.該程序能夠用于模擬鋼筋混凝土結構進入彈塑性狀態之后的非線性行為,為抗震設計和抗震性能評價提供有效的數值計算工具.
由于本文開發的材料模型不考慮鋼筋和混凝土之間的粘結滑移作用,以及鋼筋的屈曲和低周疲勞效應,因此,為了進一步提高模擬精度,開發更為精細的鋼筋混凝土材料模型是下一步需要開展的研究工作.

