基于非阻塞性顆粒阻尼技術的填充顆粒對約束阻尼結構減振性能的影響

孟凡迪，黃微波，桑英杰，呂 平，梁龍強

(青島理工大學土木工程學院，青島 266033)

振動問題在地鐵軌道、航空航天、船舶等領域中日益突出，它不僅對人們的生活造成困擾，還增加了儀器設備損耗，減少其壽命周期，甚至影響飛機和艦船的作戰能力。黃微波等[1-3]認為在基材表面敷設粘彈性材料形成自由阻尼或約束阻尼結構是一種重要的減振技術措施，為了進一步提高結構的減振性能，武迪等[4]在阻尼層與基層之間設置墊高層，通過懸臂梁模型對開槽寬度的變化所產生的振動特性進行了研究，梁龍強等[5]將聚氨酯泡沫作為隔離層，復合損耗因子顯著提高，有效抑制了結構的振動。

自20世紀90年代，Panossian[6-7]在國際會議上提出非阻塞性顆粒阻尼(non-obstructive particle damping，NOPD)技術后并成功應用到汽車葉片上，關于該項技術的研究與應用從未停止，并相繼在直升飛旋轉槳葉的模型、汽車制動鼓、英雄紀念碑和斜拉橋的繩索上應用，均取得良好的減振效果[8-11]。

現階段的研究中，結構的隔離層或約束層的材料為剛性體，在使用過程中具有局限性，當基材為圓弧形或者異型時，難以緊密地貼附在基材表面的問題一直沒有被處理。為此，現將約束阻尼結構采用環氧樹脂代替金屬鋼板作為約束層，能夠更加便利地貼附在各種異型基材表面，但環氧材料剛度較小，降低結構在振動時對阻尼層的拉伸、彎曲變形能力，為保證結構整體的減振性能不受影響，提出將NOPD技術應用到約束阻尼結構中，即在環氧材料中預先設置多個空腔并填充鋼球顆粒，當外界激勵引起結構振動時，充分發揮約束阻尼結構和顆粒阻尼技術的減振能力。

1 實驗方案

1.1 模型制備

約束阻尼結構是由基層、阻尼層、約束層三部分組成。實驗中所用的基材為Q235鋼板，市售，規格為500 mm×43 mm×3.5 mm，彈性模量2.1×105MPa，密度7 800kg/m3；阻尼層為Qtech-501黏彈性材料，約束層為Qtech-601環氧樹脂，均由青島沙木新材料有限公司提供。

阻尼層采用手工刮涂的方式制備，約束層是在預先制作好的模具中進行澆筑，腔體的位置設置在下端，雙排緊密均勻排布，共布置12個球狀腔體，半徑10 mm。選用填充顆粒的種類、密度、粒徑如表 1所示，模型示意圖如圖 1所示。構件制備完成后，置于常溫條件下養護72h，方可進行振動測試。

表 1 填充顆粒密度及粒徑Table1 Filling particle density and size

1.2 測試設備及方案

振動測試的設備主要包括DASP-V11分析系統、INV3062T0信號采集分析儀、IC壓電加速度傳感器、測試支架和砝碼，如圖 2所示。

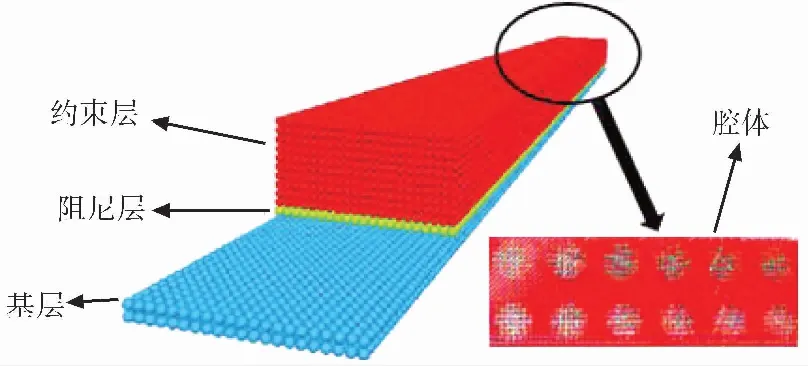
圖 1 基于顆粒阻尼技術的的約束阻尼結構Fig.1 Constrained damping structure based on particle damping

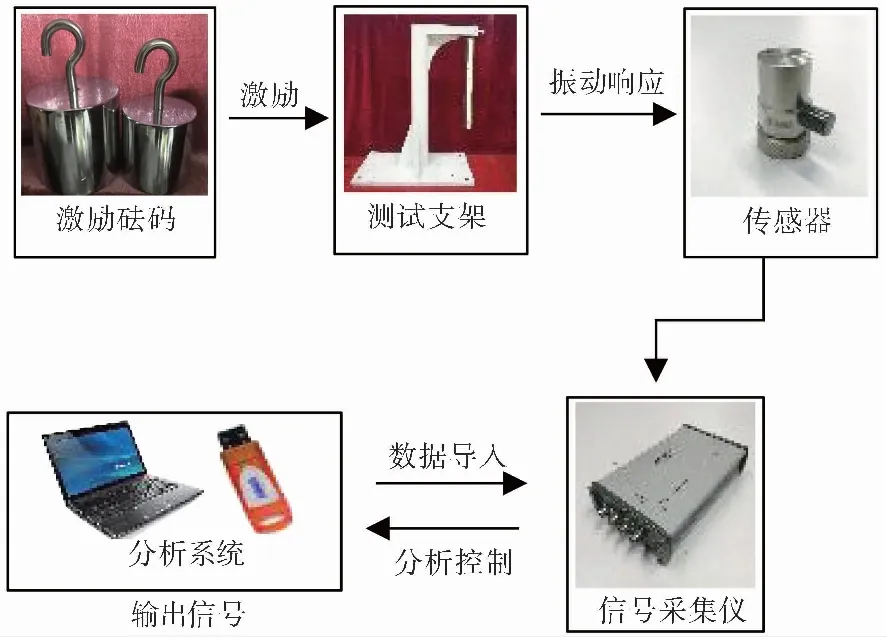
圖 2 振動測試分析系統Fig.2 Vibration test and analysis system

懸臂梁模型固定在測試支架，拾振點(傳感器安放位置)布置在距自由端35 mm處，采用尼龍繩將自由端和砝碼相連，在重力作用下使構件產生彎曲變形，通過剪斷尼龍繩的方式使預先施加的力瞬間消失，構件產生振動；采樣方式選用信號觸發，采樣頻率為512Hz，同一組變量測試三次。

2 實驗結果

2.1 顆粒填充率的影響

2.1.1 顆粒運動狀態分析

將半徑為10 mm的單個腔體固定在懸臂梁基材的自由端，分別填充10%、30%、50%、70%和90%的鋼球顆粒，采用MER-502-79U3M/C工業數字相機拍下振動過程的圖像，如圖 3所示。

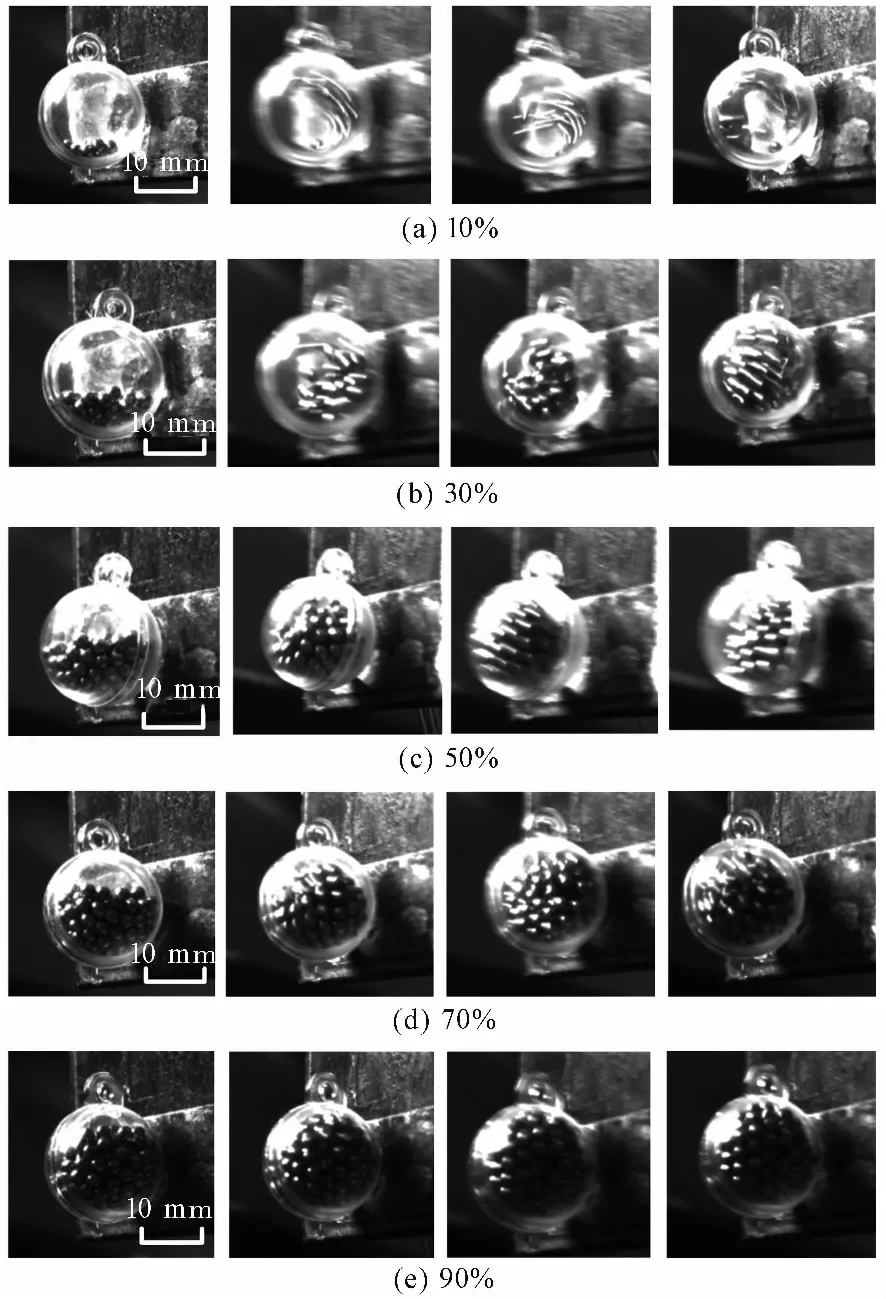
圖 3 不同填充率在振動過程中的運動狀態Fig.3 The motion state of different filling rate during vibration process

通過圖 3 顆粒在不同填充率的條件下的運動狀態分析可以發現，當受到外界激勵時，填充率為10%的腔體中的顆粒會被整體拋起，并與腔體的側壁發生沖擊碰撞，獲得更大的能量后反向加速并成弧狀運動，到達至最高點后散落并與腔體底部發生沖擊和碰撞，如圖 3(a)所示；由圖 3(b)、圖3(c)可以看出，顆粒在整個過程中始終保持整體的運動狀態，在外界激振力的作用下賦予動能，不斷與腔體發生沖擊和碰撞，顆粒具有較大的位移變化，顆粒之間擠壓成一種十分緊湊的狀態，使得全部顆粒具備較大的動能且都在進行耗能運動；由圖 3(d)、圖3(e)所示，隨著填充率的進一步增加，達到90%時，顆粒在腔體中的自由運動空間變小，在底層的顆粒甚至不發生位移變化，使得整體運動時的動能較小，顆粒之間、顆粒與腔體之間的碰撞摩擦次數降低，總體耗能隨之減少。

2.1.2 時域和復合損耗因子分析

以激振力20 N，填充顆粒粒徑2.0 mm的條件下為例，分析填充率的不同對結構減振性能的影響規律，時域變化曲線如圖 4所示，損耗因子變化曲線圖如圖 5所示。

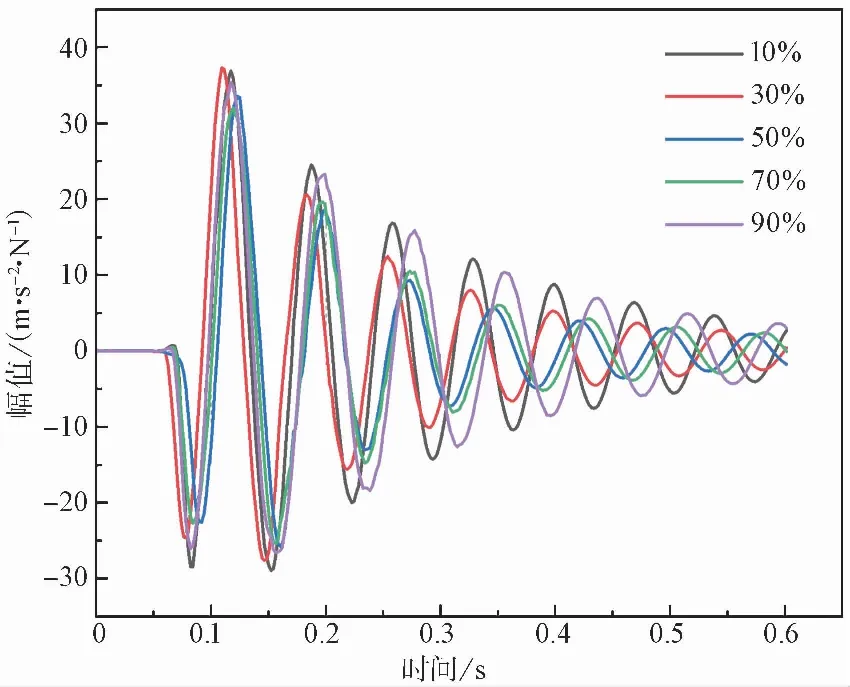
圖 4 不同填充率時的時域變化曲線Fig.4 Time domain variation curves of different fillin

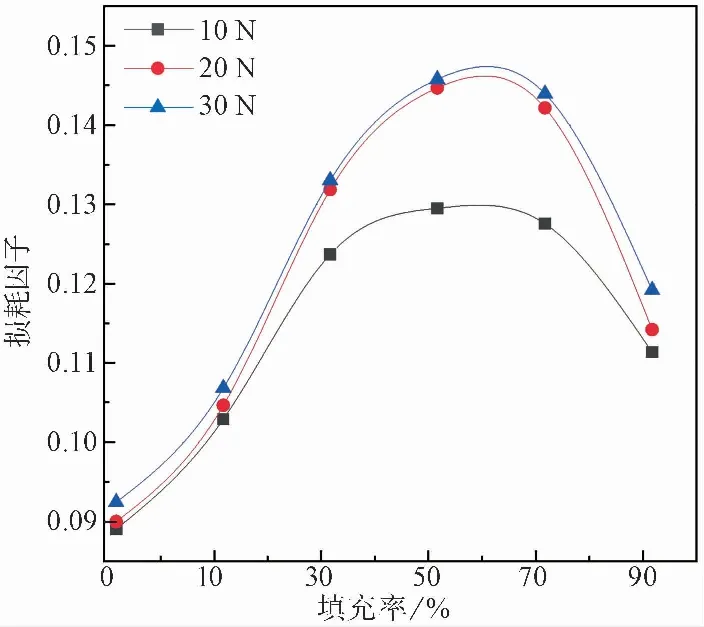
圖 5 不同填充率時的復合損耗因子Fig.5 Loss factor at different filling rate

由圖 4可知，當約束阻尼結構填充率分別為10%、30%、50%、70%和90%時，幅值由最大峰值下降到4.5m/(s2·N)時，耗費的時間為0.4219、0.3262、0.2578、0.2605、 0.3984s，耗費時間呈現先減小后增大的趨勢。其中，填充率在50%時的約束阻尼結構所耗費的時間最少，與其他幾種填充率相比分別下降了63.65%、26.53%、1.05%、54.54%。當填充率在50%和70%時峰值下降到4.5m/(s2·N)左右所耗費的時間最少，且差距并不明顯。

由圖 5可知，以外界激勵20 N為例，填充率在10%、30%、50%、70%和90%時的結構復合損耗因子分別為0.1047、0.1319、0.1447、0.1422和0.1192，較無填充顆粒的約束阻尼結構的0.0900，分別提高了16.33%、46.56%、60.78%、58.00%、32.44%。隨著填充率的增加，顆粒之間產生的摩擦和碰撞次數增加，在單次摩擦和碰撞損耗能量不變的前提下，使得總耗能增加，從而表現出更佳的減振性能，但當填充率增加到一定值時，顆粒聚集成團，流動性降低，相互之間幾乎不發生碰撞和摩擦，只起到附加質量的作用，導致振動總耗能大幅度降低。

通過對顆粒運動狀態的分析發現，當顆粒的填充率在50%之前時，腔體內幾乎所有顆粒都發生了較大的位移變化；但隨著填充率的繼續增加，腔體中自由運動的空間卻減小，導致發生耗能運動顆粒總量隨之減少，即在填充率50%時顆粒的整體耗能最為劇烈，上述對時域衰減曲線和復合損耗因子的研究中也證明：隨著填充率的增加，結構的振動響應幅值至平穩的耗時先減小后增大，復合損耗因子均呈先增大后減小的趨勢，且當填充率在50%時，較無填充顆粒的約束阻尼結構，復合損耗因子提高了60.78%，最大限度地抑制了結構的振動。另外，當外界激振力為10、30N的復合損耗因子隨填充率的增加同樣呈現先增大后減小的趨勢，且填充率在50%時復合損耗因子最大。

2.2 顆粒粒徑的影響研究

2.2.1 同材料等直徑的顆粒

以激振力20 N、填充率50%的條件為例，分析不同粒徑對結構減振性能的影響規律，復合損耗因子如圖 6所示，時域變化曲線如圖 7所示。

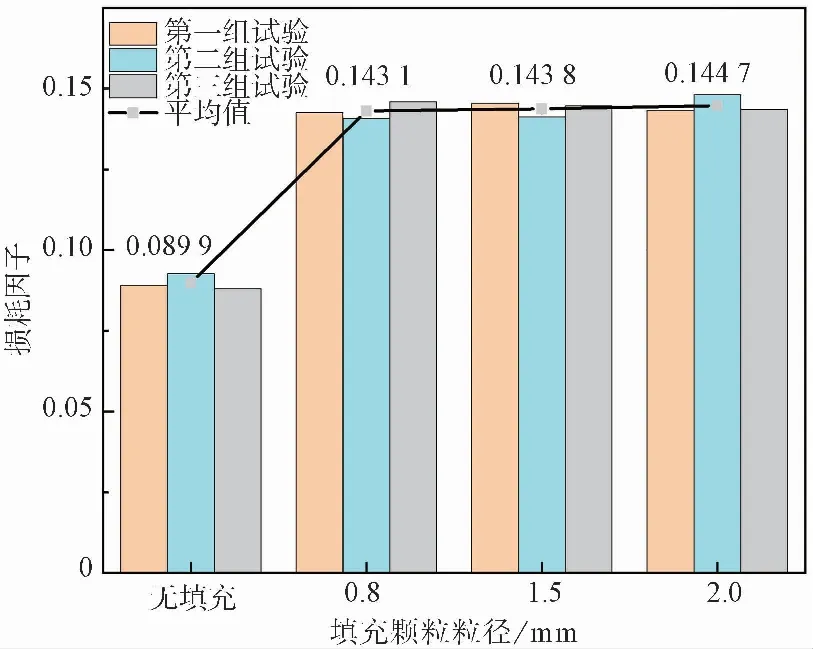
圖 6 不同粒徑填充顆粒的損耗因子Fig.6 Loss factor of filling particles with different particle sizes

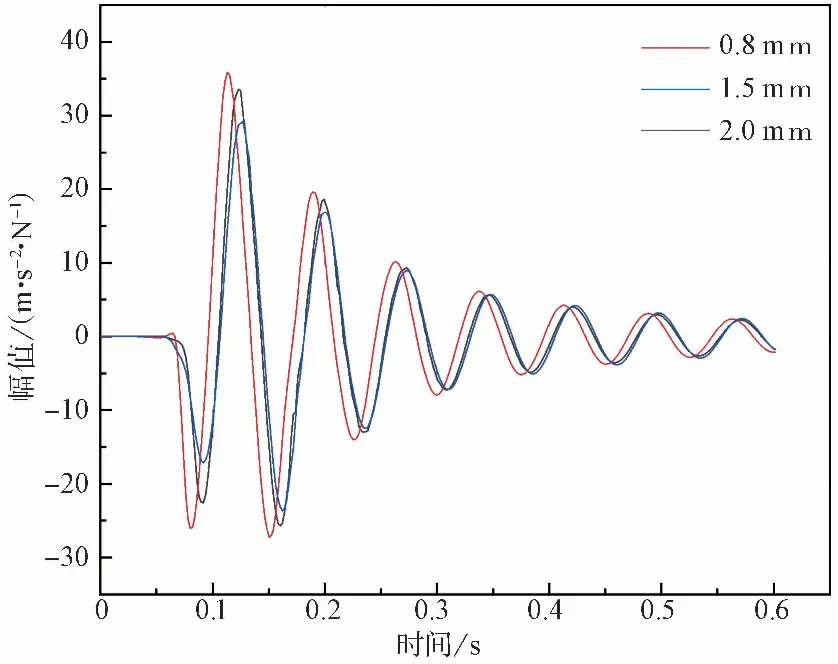
圖 7 不同粒徑填充顆粒的時域變化曲線Fig.7 Time domain change curves of filling particles with different particle sizes

由圖 6 可知，約束阻尼結構在填充率為50%、激振力為20N的作用下，填充0.8、1.5、2.0 mm鋼球顆粒時的復合損耗因子分別為0.1434、0.1438和0.1446，損耗因子最大差值僅為0.0012，較無填充顆粒的約束阻尼結構分別提高了59.18%、59.96%和60.85%，呈隨粒徑增加而略微增大的趨勢，但增大幅度并不顯著。填充顆粒粒徑的增加，單個球體被賦予的動能增加，顆粒之間單次碰撞和摩擦的耗能提高，但填充率一定的條件下，粒徑較大的顆粒填充數量必然不足，降低了顆粒間碰撞和摩擦時的次數，使得總耗能并未發生明顯提高。

由圖 7可知，約束阻尼結構在填充顆粒粒徑為0.8、1.5、2.0 mm的鋼球時，凸峰值下降到2.5m/(s2·N)左右，分別用了0.4492、0.4453、0.4473s，振動響應凸峰值趨于平穩所耗費時間幾乎相當，阻尼性能無明顯變化。同樣的，文獻[12]對兩球彈塑性碰撞的理論模型耗能原理進行分析，同材料等直徑的顆粒相互碰撞時，顆粒的直徑R對結構的復合損耗因子η無影響。最終可以得出，填充同材料等直徑顆粒的粒徑對基于非阻塞性顆粒阻尼技術的約束阻尼結構的減振性能無明顯影響。

2.2.2 同材料不等直徑的顆粒

將兩種不同粒徑的顆粒同時填充在腔體內，當外界激勵引起結構振動時，顆粒會產生分離的現象，如在生活中常采用垂直或者水平搖晃簸箕的方式分離大小不同的谷物。在沿豎直方向引起顆粒的混合系統發生振動時，通常大的顆粒向上運動，小的顆粒向下運動的顆粒分離現象稱之為“巴西果效應”；研究發現，再少些情況下，也會發生小顆粒在上，大顆粒在下的情況，稱為“反巴西果效應”，如圖 8 所示[13]。

圖 8 顆粒系統狀態隨時間變化圖Fig.8 Changes of particle system state over time

對填充兩種不同粒徑鋼球顆粒的減振性能研究時，因“巴西果效應”的影響，設置3種不同的初始狀態，如圖 9所示。

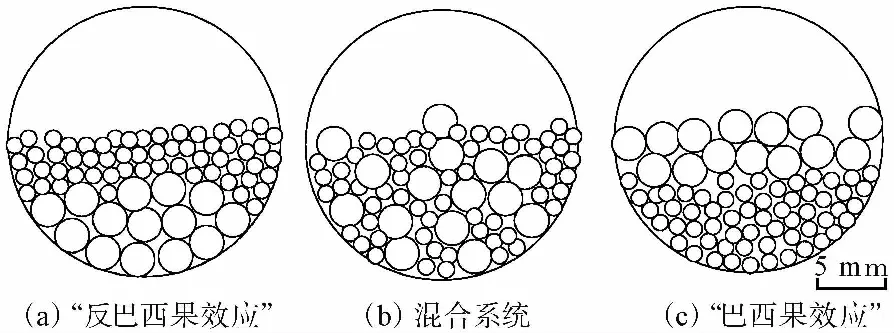
圖 9 顆粒系統初始狀態圖Fig.9 Initial state diagram of particle system

在激振力20 N、填充率50%的條件下，分析混合顆粒系統的初始狀態、填充比例的不同對結構阻尼性能的影響規律，復合損耗因子如表 2所示。

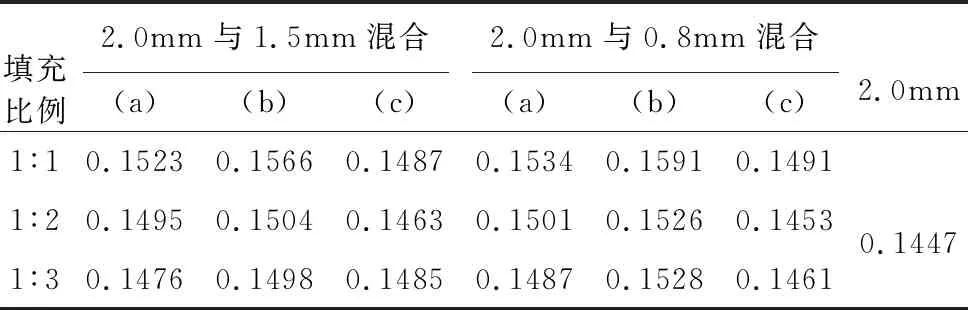
表 2 不同顆粒系統的復合損耗因子Table2 Composite loss factors of different particle systems

從表 2中可以發現，填充2.0mm鋼球顆粒時的復合損耗因子為0.1447，當摻入1.5mm或0.8mm的鋼球組成混合系統時，結構的復合損耗因子提高了0.4%～10.0%。初始狀態為如圖 9(b)的混合系統，且填充不同粒徑顆粒的質量比為1︰1時，結構的復合損耗因子最大，減振效果最佳；隨著振動過程的持續進行，會出現“巴西果效應”或“反巴西果效應”，如圖 9(a)、圖9(c)所示，此時結構的復合損耗因子降低。上述實驗結果表明：填充兩種不同粒徑的鋼球顆粒能夠使結構復合損耗因子進一步提高，但顆粒系統處于“巴西果效應”或“反巴西果效應”階段，因振動響應產生成團運動時，粒徑不同的顆粒產生分離現象，不等粒徑顆粒間的接觸面較小，導致等直徑顆粒間的摩擦和碰撞效果居多，損耗因子變化并不顯著；不同粒徑的最佳質量比為1︰1，此時不等粒徑顆粒間的接觸面積也最大；摻入粒徑更小的0.8 mm的鋼球顆粒，進一步增加了不等粒徑顆粒間的接觸面，結構的復合損耗因子也得到了進一步提高。

2.3 顆粒密度的影響研究

以激振力20 N、顆粒粒徑為2.0 mm在填充率50%的條件為例，分析顆粒密度的不同對結構減振性能的影響規律，復合損耗因子和質量變化如圖 10所示。

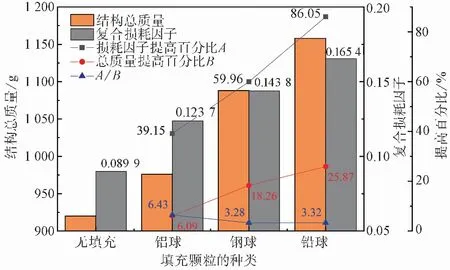
圖 10 不同密度的填充顆粒的損耗因子和質量變化圖Fig.10 Loss factor and mass change diagram of filled particles with different densities

根據圖 10可以看出，相較于沒有填充顆粒的約束阻尼結構，在填充率不變情況下，隨著材料密度的增加，復合損耗因子提高由39.15%上升至86.05%，附加質量隨之提高了6.03%～25.87%。填充顆粒密度的增加，使得單次摩擦和碰撞損耗更多的能量，提高了結構的減振性能，但與此同時也產生了更多的附加質量，由此對填充不同種顆粒情況下的單位質量增加百分比所提高的損耗因子中填充鋁球時最高，值為6.43%。在外界其他因素一致的條件下，加入相同質量的鋁球能夠更大幅度的提高結構的復合損耗因子；加入相同體積的顆粒時，填充密度較大鉛球顆粒時結構的復合損耗因子值最大，減振效果最好。

3 結論

通過對基于顆粒阻尼技術的約束阻尼結構進行運動狀態研究和振動測試，并對測試結果進行時域和復合損耗因子分析，得出以下結論。

(1)隨著填充率由10%增加至90%，基于顆粒阻尼技術的約束阻尼結構時域曲線衰減速度和復合損耗因子均呈現先增大后減小的趨勢，且當填充率為50%～70%時，阻尼性能最為理想；對顆粒運動狀態研究發現，填充率在10%～50%時的顆粒運動最為劇烈，幾乎全部顆粒都參與了耗能運動，隨著填充率進一步增加，腔體內空間的不足限制了顆粒的運動，阻尼性能降低。

(2)對于填充相同材料等粒徑的顆粒而言，懸臂梁結構的復合損耗因子與顆粒的直徑無關，其中時域衰減曲線凸峰值下降到2.5m/(s2·N)耗時僅差0.0039s；復合損耗因子極差值僅為0.0015；將不同粒徑的鋼球顆粒混合在一起研究發現，復合損耗因子進一步提高，不同粒徑顆粒間的接觸面最大時，提高最為顯著。

(3)在外界其他因素一致的條件下，填充顆粒質量相同時，密度較小的鋁球減振效果最好，控制體積不變時，密度較大的鉛球復合損耗因子值最大，減振效果更佳。