基于計算流體力學-離散單元法耦合的粗糙壁面顆粒趨壁沉積過程的數值模擬

劉 巖，秦 攀，洪文鵬

(1. 中電華創(蘇州)電力技術研究有限公司，蘇州 215123； 2. 東北電力大學能源與動力工程學院，吉林 132012)

細微顆粒物在日常生活和生產中普遍存在。粒徑小于10μm的顆粒能夠進入上呼吸道甚至深入肺部，引起呼吸系統疾病[1-2]；而10μm以上的顆粒沉積在室內會導致材料退化，如藝術品和電子設備受損[3]，如何降低室內顆粒物濃度成為當前建筑環境研究領域的熱點問題之一。建筑物中的通風和空調系統作為室內外空氣交換的主要場所，室內顆粒濃度與顆粒在通風和空調系統管道中的輸運及沉積現象密切相關[4]。

近幾十年來，許多學者從理論、實驗和模擬3個方面對粗糙壁面顆粒沉積機理和求解方法開展了大量研究。發現雖然通過理論[5-6]和實驗[7-10]得到的顆粒沉積速率和無量綱弛豫時間關系曲線變化趨勢一致，但是無量綱沉積速率差值最大達到1～2個數量級[4-9]。理論研究更多是根據實際經驗得到半經驗解，而實驗很難捕捉到所有重要信息，因此，僅通過理論和實驗對粗糙壁面顆粒行為研究具有一定挑戰。

目前計算流體力學(computational fluid dyna-mics，CFD)對顆粒沉積應用比較廣泛，能夠提供更詳細的流場和顆粒行為信息。采用直接數值模擬、大渦模擬和分離渦模擬方法進行求解計算成本過高，只有部分學者采用此方法對粗糙壁面表面粗糙度、顆粒再懸浮和多層沉積過程進行研究[11-14]。相比以上3種方法，雷諾應力模型應用最為廣泛。學者們主要通過改變粗糙元布置方式[15-18]、形狀[19-20]、間距和高度[18，21]，探索粗糙壁面多層沉積、顆粒沉積規律和不同位置沉積情況，還有學者采用Hertz-Mindlin接觸模型對大粒徑、非球體顆粒運動規律進行初探[22-23]。

然而，以往對粗糙壁面顆粒沉積的研究大多簡化了顆粒沉積條件，即假設顆粒接觸壁面就會無條件發生沉積或沒考慮黏附作用，但實驗研究表明，即使是微米級顆粒，也會出現反彈現象，并且微米級顆粒間還存在黏附作用[24-25]。

因此，現采用計算流體力學-離散單元法(discrete element method，DEM)[26]耦合方法，模擬顆粒沉積過程，充分考慮顆粒-顆粒、顆粒-壁面間的接觸碰撞、反彈和黏附作用，對光滑和粗糙壁面顆粒沉積進行模擬，分析顆粒粒徑、碰撞力、黏附力和二次流對顆粒沉積的影響，探索粗糙壁面顆粒趨壁沉積行為機理，不僅對促進氣固兩相流動與沉積規律的研究有一定的理論依據，還對室內空氣品質的改善和其他相關應用具有一定的指導意義。

1 動態沉積模型

顆粒在壁面附近運動包括在流場中運動、沿壁面滑動和與壁面接觸黏附或反彈3個過程，采用CFD-DEM耦合模型進行模擬，首先在Fluent中對氣相進行求解，隨后在EDEM軟件中對顆粒相進行計算，通過Fluent中UDF和EDEM中API接口實現耦合連接，部分耦合代碼如圖 1所示。

圖 1 部分耦合代碼Fig.1 The part of the coupled code

1.1 氣相模型

氣相視為不可壓縮流體，流體連續性方程和動量方程分別為

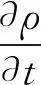
(1)

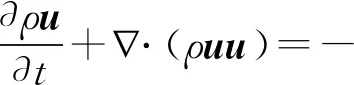
(2)

式中：ρ為空氣密度；t為時間；u為空氣速度；μ為空氣動力黏度；V為CFD網格單元的體積；FD為曳力，是顆粒物在流道中運動和沉積的主導作用力。

1.2 顆粒相模型

1.2.1 顆粒運動模型

顆粒受力包括重力、曳力、Saffman升力、顆粒-顆粒、顆粒-壁面之間的碰撞力和黏附力，顆粒發生碰撞和黏附及其受力示意圖如圖 2所示。

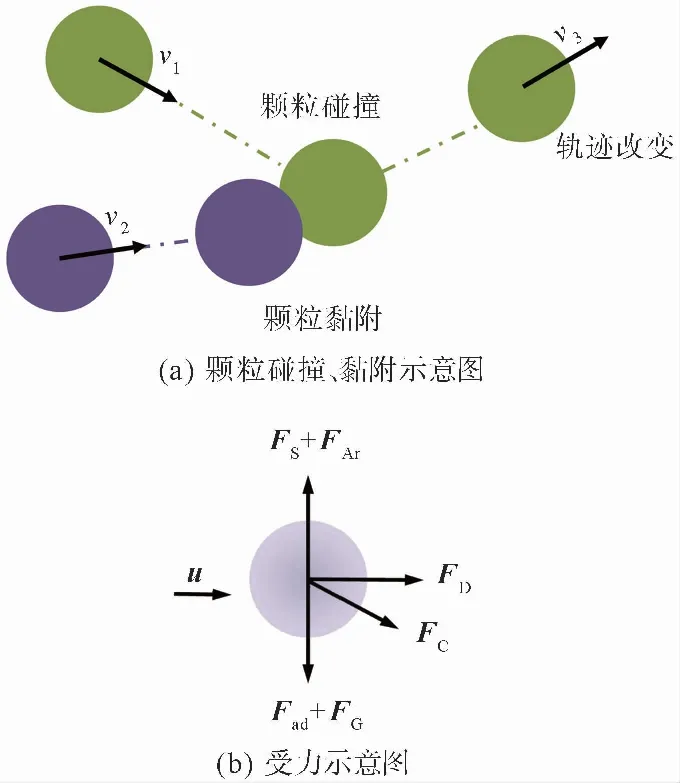
圖 2 顆粒碰撞、黏附和受力示意圖Fig.2 Schematic diagram of particle collision，adhesion and force

顆粒的運動方程為

(3)

式(3)中：mp為顆粒質量；up為顆粒運動速度；FG為重力；Fad為黏附力；FC為顆粒受到的碰撞力；FS為Saffman升力；FAr為阿基米德浮力。

1.2.2 JKR接觸模型

采用Hertz-Mindlin with JKR Cohesion[27]接觸模型，考慮接觸區域內范德華力對顆粒-壁面、顆粒-顆粒間的黏附作用，粒子黏附產生的力基于重疊量、相互作用參數和表面能，公式為

(4)

(5)

式中：E*為當量彈性模量；R*為當量半徑；α為接觸半徑；γ為表面能；δ為顆粒間重疊量，當顆粒與壁面接觸時，視壁面為無窮大顆粒。

2 模擬條件

計算區域是三維底面布置矩形橫肋的粗糙流道(160 mm×20 mm×20 mm)，底面均勻布置7個間距為20 mm的橫肋粗糙元結構，粗糙元高度e為2mm，計算域如圖 3所示。為了減少計算量和仿真時間，采用邊界函數分布法對入口速度和湍動能進行初始化；出口采用自由出流邊界；在距離流道入口3R(R為顆粒半徑)處均勻釋放顆粒，當顆粒全部沉積或流出流道視為模擬結束，主要模擬參數如表 1所示。

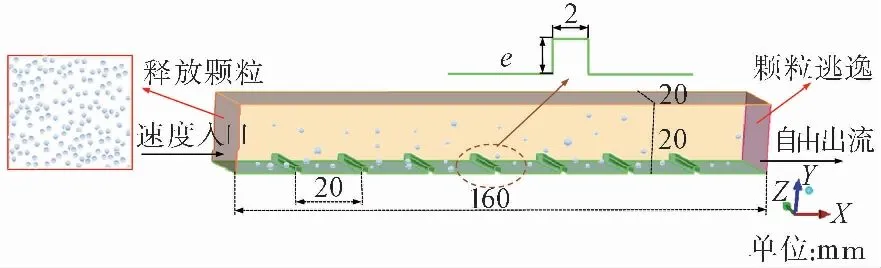
圖 3 計算域Fig.3 The computational domain

表 1 主要模擬參數Table1 The main simulation parameters

使用ICEM軟件對模型進行網格劃分，粗糙結構的存在使得流場變得復雜，為準確預測顆粒-壁面的相互作用，對近壁面網格進行加密，第一層網格高度為0.05mm，第一層網格質心到壁面的無量綱距離y+為1.2，增長因子為1.2，結構化網格，考慮到計算代價和準確性等因素影響，經網格無關性驗證，如圖 4所示，采用網格數為59.8×104的模型進行計算。

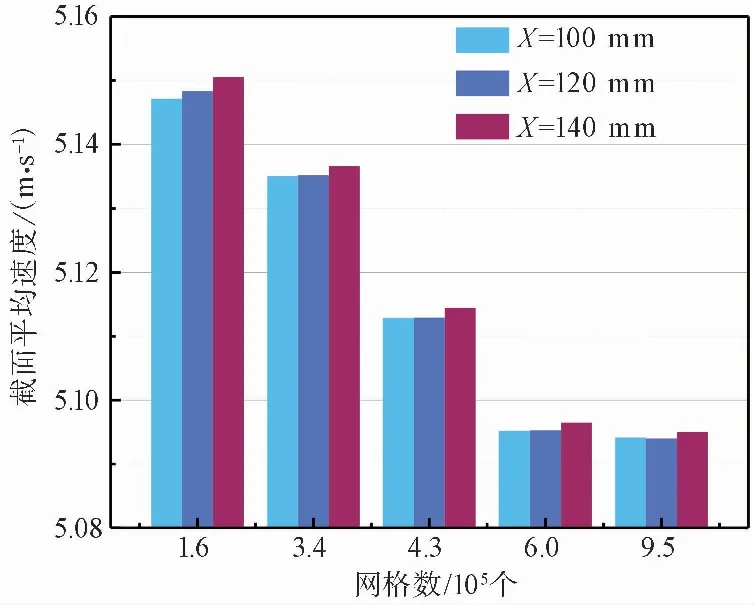
圖 4 網格無關性驗證Fig.4 Grid independence verification

圖 5 粗糙結構間氣流速度分布Fig.5 The air velocity distribution between rough structures

3 模型驗證

3.1 湍流場

精確的湍流場是研究顆粒沉積的基礎，有研究表明，流場在第Ⅳ個粗糙結構后趨于穩定。因此選取第Ⅵ和第Ⅶ個粗糙結構間氣流速度與實驗值[28]進行對比，發現吻合較好，如圖 5所示，說明采用雷諾應力模型可以準確預測粗糙流道的湍流場。

3.2 數值算法驗證

(6)

式(6)中：h為計算域高度；U0為平均流速；Ndep為壁面沉積的總顆粒數目；Nin為進入流道總顆粒數；u*為湍流摩擦速度；L為計算域的長度。

基于流動內時間尺度的無量綱顆粒弛豫時間[30]為

(7)

式(7)中：S為氣固密度比；dp為顆粒直徑；Cc為坎寧漢系數；ν為空氣動力黏度。

為了驗證數值算法的正確性，將光滑壁面顆粒無量綱沉積速率與經典模擬[31-32]和實驗值[33-34]進行對比，吻合較好，如圖 6所示。因為顆粒與壁面為點接觸，因此采用的JKR模型同樣可以準確預測粗糙壁面顆粒沉積情況。

4 結果與討論

4.1 氣相流場

微米級顆粒受流場影響程度較大，研究顆粒在流場中的運動情況，首先對流場進行分析。

從圖 7光滑和粗糙流道湍動能和流線分布可以看出，氣流在流經粗糙結構時邊界層發生分離，使粗糙結構附近出現大小不一的湍流旋渦，增加對顆粒的卷吸作用，并且有垂直于流動方向的湍流脈動速度，顆粒趨壁速度得到提高，粗糙流道最大湍動能達到光滑流道湍動能的6.97倍，而光滑流道的流線幾乎與X軸平行，更易攜帶顆粒流出流道，不利于顆粒沉積。

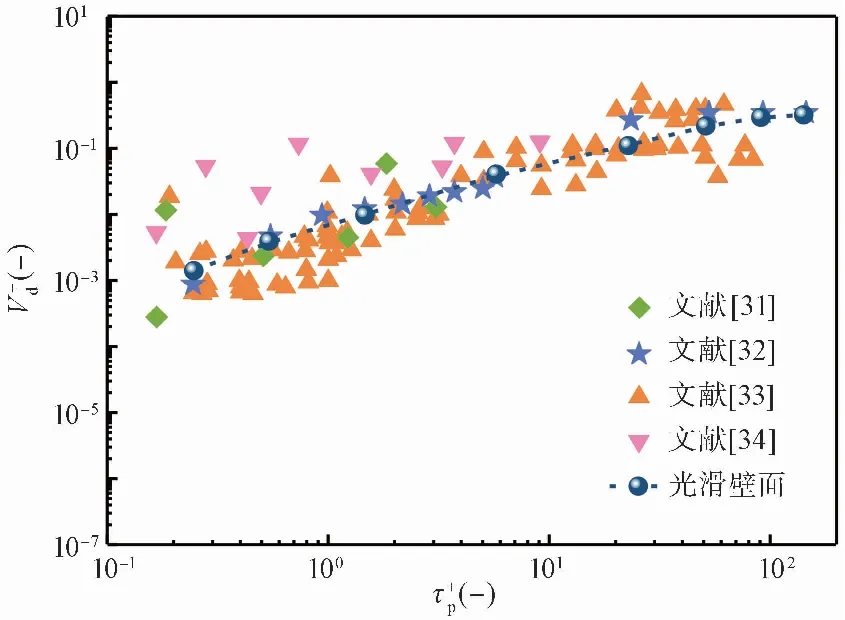
圖 6 光滑壁面無量綱沉積速率對比驗證Fig.6 Comparison and verification of non-dimension deposition velocity on smooth surface

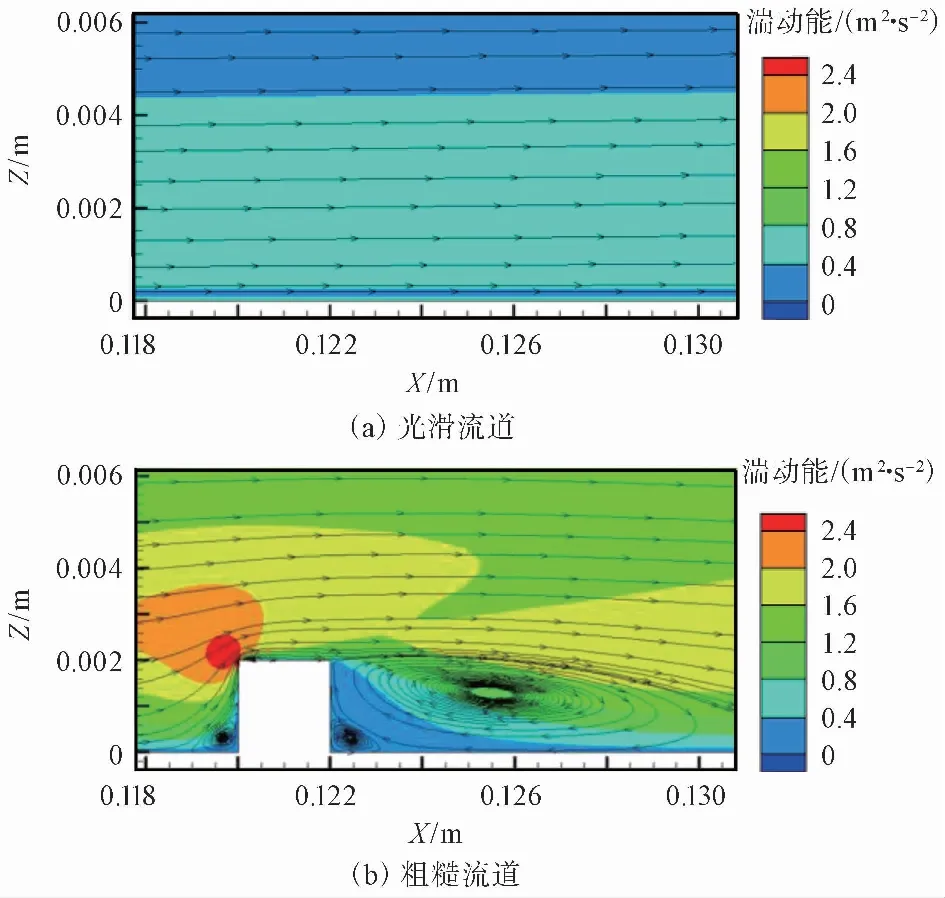
圖 7 光滑和粗糙流道湍動能和流線分布Fig.7 Turbulent kinetic energy and streamline distribution on smooth and rough surface

4.2 粗糙結構對顆粒沉積影響

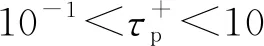
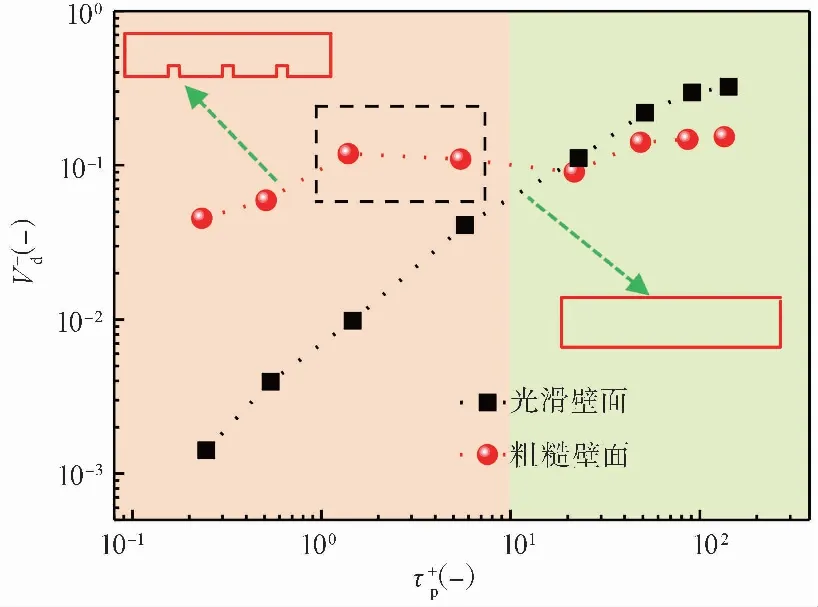
圖 8 粗糙和光滑壁面顆粒無量綱沉積速率對比Fig.8 The comparison of particle deposition velocity on rough and smooth surfaces

圖 9 2μm和3μm顆粒運動軌跡Fig.9 2μm and 3μm particle trajectories

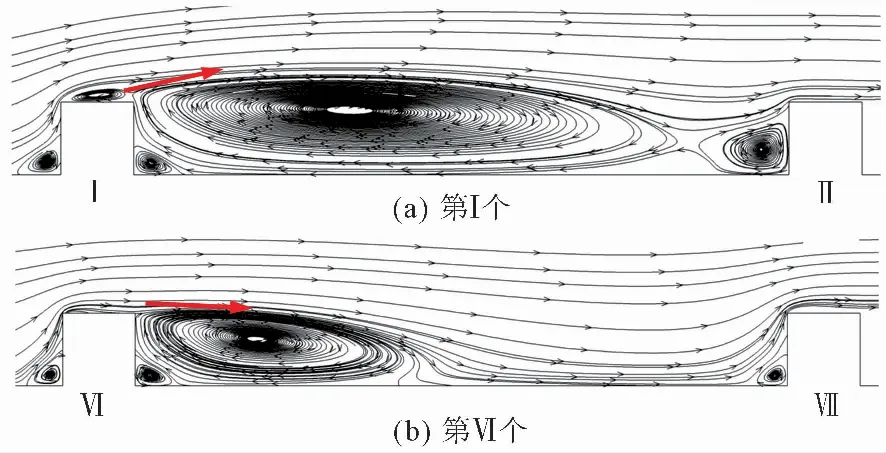
圖 10 第Ⅰ個和第Ⅵ個粗糙結構附近旋渦回流Fig.10 Vortexes near the first and the sixth rough structure

圖 11 50μm顆粒運動軌跡Fig.11 50μm particle trajectory

4.3 碰撞力和黏附力對顆粒沉積影響

為進一步探索顆粒沉積機理，首先從顆粒能夠與壁面接觸數進行分析，經統計，50μm顆粒與壁面接觸數為2μm顆粒與壁面接觸數的8.9倍，而50μm顆粒沉積速率僅是2μm的3.4倍，顆粒運動情況不僅受氣相流場影響，還與顆粒-壁面間碰撞力和黏附力有關。圖 12(a)、圖12(b)分別為2、5μm顆粒-壁面間黏附力和碰撞力對比情況，對于2μm的較小顆粒而言，其與壁面碰撞力和黏附力大小相當，因此旋渦卷吸是使小顆粒沉積的主要因素；而對于50μm相對粒徑較大顆粒，在0.05s，顆粒全部發生沉積或沿壁面滑動，在0.05s之前，顆粒-壁面碰撞力明顯大于黏附力，說明顆粒-壁面碰撞是使顆粒沉積速率減小的主要原因，而黏附力和自身慣性是顆粒沉積的主要因素。

圖 12 顆粒-壁面作用力對比Fig.12 Comparison of the particle-wall forces

4.4 二次流對顆粒沉積影響

由于法向和展向壁面的剪切作用，氣相在沿著主流方向運動過程中發生邊界層分離，使得在垂直于流動方向橫截面上壓力分布不均，流道壁面與流道中心之間壓力不平衡，壓力梯度驅使氣相在流道壁面與流道中心之間對流流動，形成二次流，其現象如圖 13所示。由于粗糙元的存在使得粗糙流道只在底部產生兩個明顯的旋渦，卷吸顆粒使其在底面兩側附近聚集。為了更直觀地看到二次流對不同粒徑顆粒沉積情況的影響，分別選取粒徑為5、20、50μm的顆粒進行分析，顆粒沿X方向上的沉降情況的概率密度ζ(顆粒沉積數/顆粒總數)分布如圖 14所示。由此看出5μm顆粒均勻分布在壁面兩側，壁面中間位置基本不發生顆粒沉積，20、50μm的顆粒沉積絕大部分發生在粗糙壁面兩側附近，在壁面中間位置會有少部分沉積，在兩側壁面附近，50μm顆粒的概率密度將達到5μm的34倍。這是因為小顆粒由于自身慣性低而容易受到湍流二次流的影響，隨著顆粒直徑的增大，受重力和慣性的影響越大，越不容易被渦卷吸，從而發生沉積。

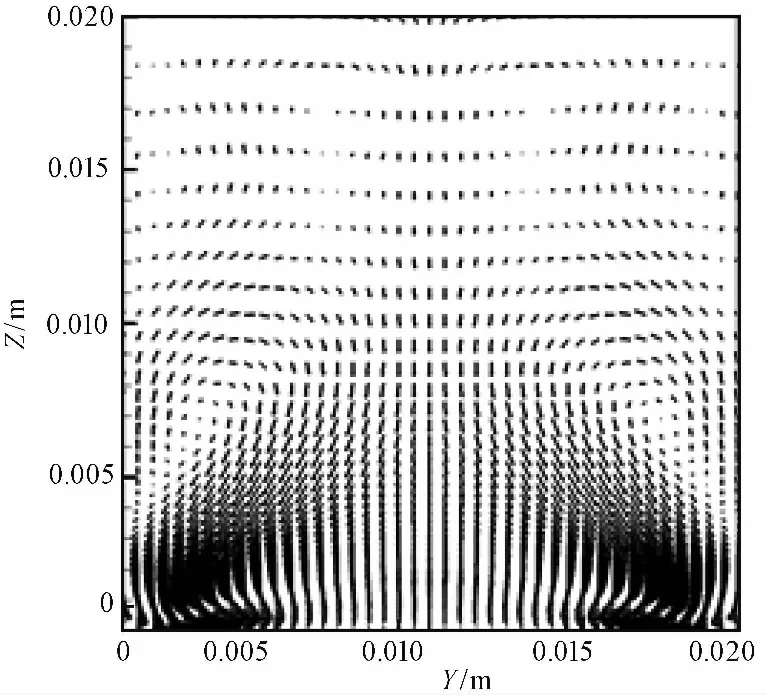
圖 13 粗糙流道二次流矢量分布Fig.13 The secondary flow vector distribution in rib-roughened channel

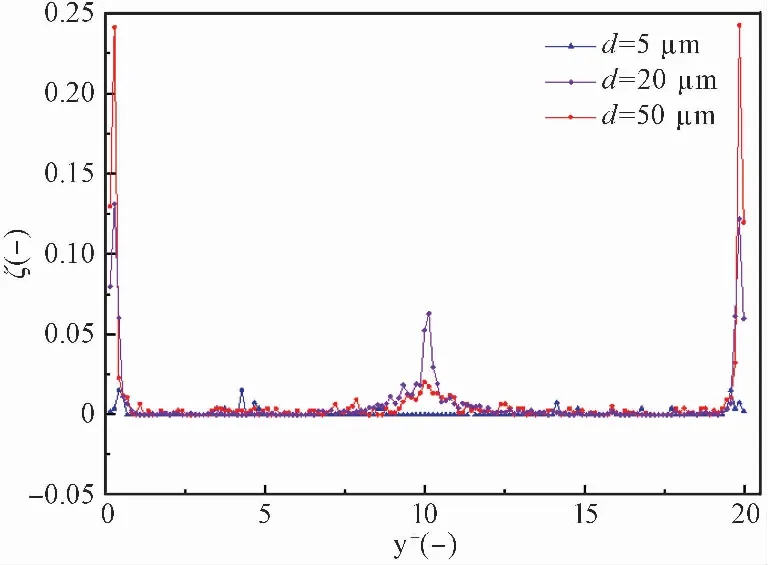
圖 14 顆粒沿X方向上沉降情況的概率分布Fig.14 The particles probability density distribution in the X direction

5 結論

采用計算流體力學(CFD)-離散單元法(DEM)耦合模型對三維矩形光滑壁面和布置橫肋粗糙壁面的顆粒沉積進行模擬計算，分析了單分散顆粒沉積過程，在研究分析過程中得出在渦擴散碰撞區，粗糙壁面顆粒沉積速率大于光滑壁面顆粒沉積速率，特別是對于粒徑為2μm的顆粒，粗糙壁面顆粒沉積速率達到光滑壁面的32倍；在慣性緩沖區，由于大顆粒碰撞作用較為強烈，使得粗糙壁面顆粒沉積速率反而小于光滑壁面顆粒沉積速率。由于二次流的影響，使得較小粒徑顆粒均勻沉積在壁面兩側，中間位置幾乎不發生沉積，而對相對粒徑較大顆粒，大部分顆粒沉積在壁面兩側，有少部分顆粒沉積在壁面中間位置，并且在壁面兩側，50μm顆粒的概率密度將達到5μm的34倍。