基于MATLAB/Simulink的氫燃料電池系統建模與仿真

張可健, 曲大為, 蘭洪星, 于 鋒

(吉林大學汽車仿真與控制國家重點實驗室，長春130022)

質子交換膜燃料電池具有眾多突出的優點，如能量轉化率高、能量密度高、噪聲低以及零排放等，可以廣泛應用于列車、飛機、汽車等交通工具及便攜式移動電源等場合[1]。質子交換膜燃料電池系統兼具高效率、高能量密度、高度清潔、大滯后性、非線性、時變性等特點，系統工作過程中涉及電化學、熱力學、流體力學、傳熱傳質理論等。目前中外學者建立的燃料電池系統模型主要包括機理模型、經驗模型和半經驗模型，其中以機理模型居多。

最早的燃料電池建模工作始于20世紀90年代，Springer、Bernardi和Verbrugge等先驅者建立了燃料電池一維模型，提出了解釋水分通過膜的機制，并提出了膜電導率與膜中含水量之間的關系，同時對燃料電池的性能進行了初步研究[2]。Zhang等[3]基于建立的燃料電池供氣的一維仿真模型，對空氣壓縮機與燃料電池系統的匹配特性進行了分析，得出設計人員應注重擴展喘振邊界，在有限的設計轉速下將高效工作區域擴大到低質量流量區域，而不是僅僅擴大有效工作范圍的結論。吉林大學雷宗坤[4]基于某電堆設計參數建立燃料供給系統以及輸出特性的動態模型，針對特定電流需求條件下的電堆工作點分布與流量-壓力特性進行仿真，并基于壓力補償對系統進行控制優化。東北大學馬冰心[5]基于系統的機理模型，采用MATLAB/Simulink搭建燃料電池系統仿真平臺，圍繞燃料電池氧化劑供給控制算法展開研究，通過優化控制器參數得到穩定的系統輸出凈功率。

針對上述問題，采用單一的建模方法難以準確地得到一個可以描述實際系統的數學模型。現采用機理建模和辨識建模相結合的方式對模型進行推算，反映電堆工作壓力、電堆溫度、陰陽極工作壓力差和氧氣過量比等電池運行關鍵參數的靜態和動態響應過程以及繪制出不同工況下電池的輸出性能隨負載電流的變化曲線圖。

1 氫燃料電池輸出電壓模型

燃料電池可以直接將化學能轉化為電能，其理論輸出最大電壓為熱力學理論電動勢，即開路電壓。但是由于燃料電池自身的結構特點及電化學反應本身，使其存在三項不可逆損失，分別是活化極化電動勢、歐姆極化電動勢和濃差極化電動勢。輸出電壓模型如圖1所示。

正是由于極化現象的存在，使得燃料電池的實際輸出電壓總是小于理論值，燃料電池實際的輸出電壓可以表示為熱力學理論電動勢與極化現象產生的電壓損失的差值[6]，即

V=Enernst-Eact-Eohmic-Econ

(1)

式(1)中：V為燃料電池單體的實際輸出電壓；Enernst為燃料電池單體的熱力學理論電動勢；Eact為燃料電池單體的活化極化電動勢；Eohmic為燃料電池單體的歐姆極化電動勢；Econ為燃料電池單體的濃差極化電動勢。

在燃料電池輸出電壓模型的研究中，熱力學理論電動勢一般由能斯特方程表示，能斯特方程根據陰陽極側燃料的分壓力及溫度參數，可以推導出燃料電池單體的熱力學理論電動勢，又稱能斯特電動勢，其表達式為

(2)

式(2)中:ΔG為吉布斯自由能，ΔG=237180J/mol；ΔS為標準摩爾熵，由于反應中溫度被認為是定值，故熵的變化量近似認為是一個常數，被設為標準值[7]，ΔS=-163.15mol·K；PH2、PO2分別為氫氣分壓力、氧氣分壓力，Pa；F為法拉第常數，F=96485C/mol；T為反應過程中的熱力學溫度，K；T0為參考溫度，取為298.15K；R為通用氣體常數，取為8.3145J/(mol·K)。

活化極化是一種電極電化學反應遲延造成的電極電位偏離平衡電位的現象，活化極化現象的產生是由于電化學反應過程中，需要消耗能量打破參與反應的物質的化學鍵，引起了電子的轉移，能量的消耗就帶來了電壓的損失。陰陽極的活化極化電動勢由Butler-Volmer表示為

(3)

式(3)中：Eact，a為陽極活化極化過電勢；Eact，ca為陰極活化極化過電勢；α為電荷傳輸系數，通常取0.5；i0為交換電流密度，陰陽極兩側的氧化還原反應速度相差較大，交換電流密度也相差較大，通常陰極的交換電流密度要比陽極的交換電流密度低約5個數量級，故活化極化對電池的影響，一般忽略陽極[8]。

歐姆極化損失遵循歐姆定律，且隨著電流密度的增大而增大，則歐姆極化損失可以表示為

Eohmic=IRohmic

(4)

式(4)中：I為燃料電池的輸出電流；Rohimc為燃料電池單體的內阻，燃料電池單體的內阻主要來自質子交換膜的等效阻抗RM和質子電子轉移過程中的阻抗RC，即

Rohmic=RC+RM

(5)

質子交換膜的等效阻抗的表達式為

RM=ρMl/S

(6)

式(6)中:l為質子交換膜的厚度；S為質子交換膜的有效活化面積；ρM為質子交換膜的電阻率，是質子交換膜水含量和電池運行溫度的函數，其表達式為

(7)

式(7)中:Tst為燃料電池運行溫度；ν為質子交換膜的含水量，仿真膜含水量假設為100%。

濃差極化現象一般發生在高電流密度區域，質子在通過交換膜時，膜附近質子濃度升高，在濃度梯度的作用下，質子向低濃度區域擴散，形成邊界層，產生濃差極化電動勢。

濃差極化電動勢的大小與燃料電池的結構及工作狀態相關，其表達式為

(8)

式(8)中：imax為極限電流密度，即所用燃料電池能達到的最大電流密度，一般可以達到2.2A/cm2。

2 氫燃料電池管道模型

氫燃料電池系統模型中，氣體管道模型主要包括供給管道模型和返回管道模型。供給燃料經電磁閥流出后進入供給管道，經過加濕器處理后進入電堆，對于空氣來說，參與反應之后的廢氣需通過返回管道排出電堆，對于氫氣來說，尾端采取封閉結構，則無氣體排出，維持電堆內部參與反應的燃料的分壓力及電堆內部的水平衡。質子交換膜燃料電池(proton exchange membrance fuel cell, PEMFC)的陰陽極兩側的供給管道模型基本一致，區別僅為管道內部流體不同，這里僅介紹陰極供給管道模型。

燃料電池供應管道模型指供氣管路的集總體積，可以將供氣系統從空氣入口到電堆陰極所有管路及閥件理解為該模型之中[9]。供氣管路中的氣體壓力變化可以根據質量守恒定律描述為

(9)

式(9)中：Psm為供氣管路的壓力；Tsm為供氣管路中的氣體溫度，由于供氣管路的出口直接進入電堆，故這里用電堆溫度來代替供氣管路中的氣體溫度；Vsm為供氣管路的集總體積；Matm為入口干空氣的摩爾質量；Wsm.in為供給管道入口的空氣質量流量；Wsm.out為供給管道出口的空氣質量流量。

由于進氣管路中的壓力與電堆內的壓差較小，故可以認為供給管道出口的空氣的質量流量與電堆和管道內的壓差成線性關系，可表示為

Wsm.out=ksm.out(Psm-Pca)

(10)

式(10)中：Pca為電堆陰極的壓力；ksm.out為管道的流量系數。

返回管道即出氣管道，反應后的廢氣經出氣管道及尾排閥從電堆排出到大氣中。返回管道模型僅對于陰極，對于陽極側來說，由于采用死端方式，故不對出氣管道建模。出氣管道模型同供給管道模型類似，根據質量守恒定律，其動態模型可以描述為

(11)

式(11)中：Prm為出氣管路的壓力；Vrm為出氣管路的集總體積；Tst為出氣管路中的氣體溫度，由于出氣管路的溫度與電堆內的溫度相差不大，故這里用電堆溫度來代替出氣管路中的氣體溫度；Matm為入口干空氣的摩爾質量，Wrm.in為陰極流道出口的空氣質量流量；Wrm.out為出氣管道出口的空氣質量流量。

由于出氣管道壓力與大氣壓力值相差較大，故陰極出氣管道出口采用非線性的噴嘴方程來確定出口流量大小，即

(12)

式(12)中：CD為管道卸流系數；AT為出口處的截面積；Trm為出氣管道內的氣體溫度，模型中近似為電堆的溫度;γ為空氣熱比率系數；Prm為出氣管路的壓力；Wrm.out為出氣管道出口的空氣質量流量。

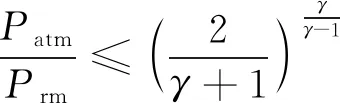
3 氫燃料電池凈功率模型

氫燃料電池堆的輸出功率可以表示為各個電池單體功率的和，假設電池單體的發電情況基本一致，則燃料電池堆的輸出功率可以表示為

Pout=VoutI=nVI

(13)

式(13)中：n為燃料電池堆單體的數目。

在氫燃料電池系統中，一般空氣由空壓機提供，空壓機的能耗來源于燃料電池所產生的能量，氧氣過量比越高，則帶來的空壓機的功耗相應增加，空壓機的能耗一般比較高不容忽視。

根據文獻[11]可知，空壓機等熵功率模型可以表示為

式(14)中：Cp為空氣的恒壓熱容；ηcp為空壓機等熵效率；P0為大氣壓力；γ為空氣熱比率系數。

凈功率模型忽略其他電子附件的能耗，如水泵、電磁閥等，可以表示為系統的輸出功率與空壓機功率模型的差值，即

Ppure=Pout-Pcp

(15)

根據已搭建完成的氫燃料電池測試系統對建立模型進行模型驗證，采集不同工況下的試驗數據繪制燃料電池極化曲線，并與仿真結果對比，仿真過程中主要參數如表 1所示。

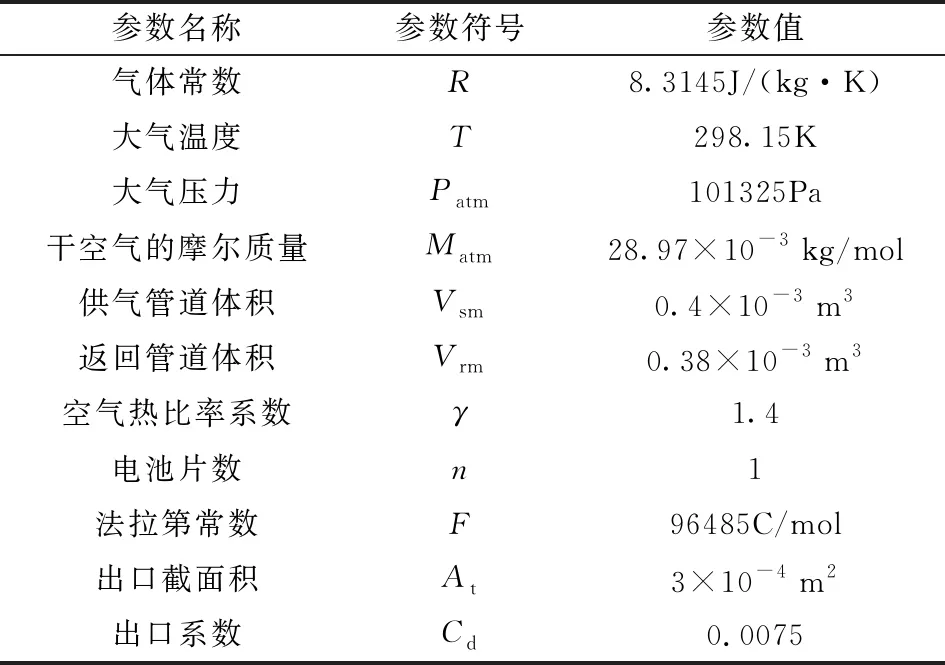
表 1 氫燃料電池系統模型參數Table 1 Hydrogen fuel cell system model parameters

仿真與試驗過程中，采用工況為：氧氣過氧比為2，環境溫度保持25℃，電堆溫度保持60℃，陽極側壓力比陰極側壓力高2×104Pa，陽極側壓力隨陰極側壓力大小改變，負載電流在0～300A，對應燃料電池電流密度為0～1.2A/cm2。

仿真曲線與試驗數據對比如圖 2所示。

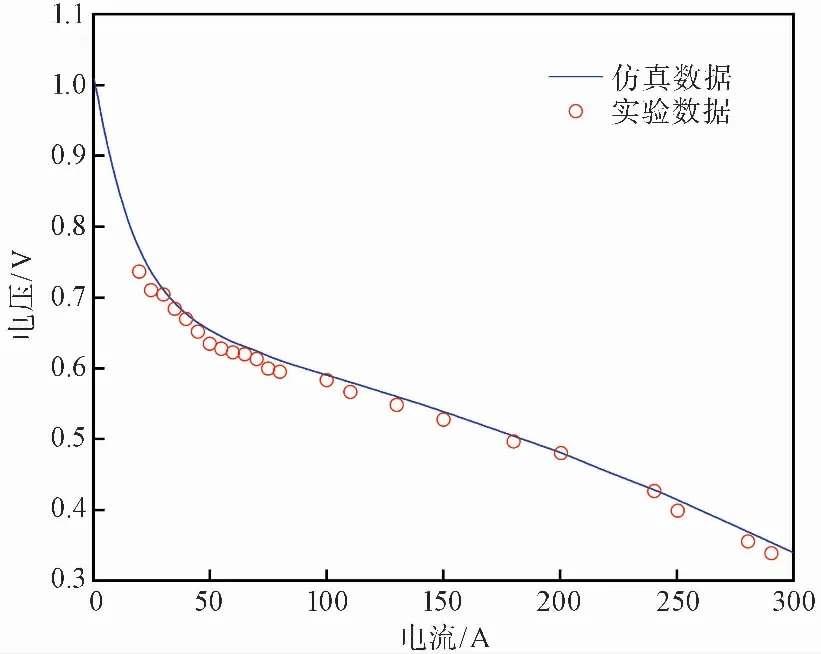
圖 2 仿真數據與試驗數據對比圖Fig.2 Comparison diagram of simulation data and test data

試驗數據在極化曲線曲率變化較大區域加密了采樣點，燃料電池空載時的開路電壓可達1.1V。在低電流密度區域，活化極化的影響顯著，由于試驗過程中電堆溫度分布不均，質子交換膜潤濕狀況差等因素的影響，電堆內阻增大，試驗數據點整體略低于仿真結果；在中間電流密度區域，歐姆極化的影響顯著，試驗數據點均勻分布在仿真曲線附近，誤差較小；在高電流密度區域，因為燃料電池內部水濃度較高，反應生成的水覆蓋于催化劑表面不能及時排出，所以濃差極化的影響顯著。綜上所述，試驗數據點的趨勢與極化曲線一致，在誤差允許范圍之內，模型符合燃料電池的運行情況。

4 氫燃料電池系統模型仿真結果分析

4.1 穩態性能分析

4.1.1 陰陽極壓差的影響

設置電堆溫度為40℃，陰陽極壓差分別為0、1×104、2×104Pa。仿真結果如圖 3所示。

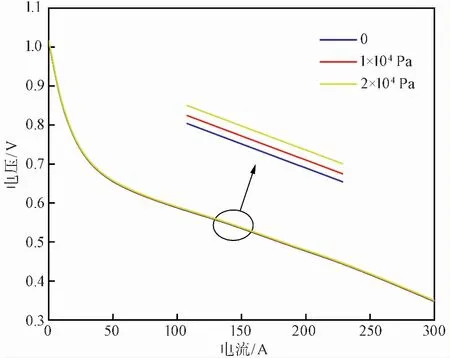
圖 3 不同陰陽極壓差下輸出電壓隨負載電流的變化曲線Fig.3 Variation curve of output voltage with load current under different cathode and anode pressure difference

由圖 3可以看出，隨著負載電流的增大，電堆輸出電壓在不同的陰陽極壓差下性能表現接近，再將曲線局部放大之后，可以看出，在負載電流相同時電堆的輸出電壓以及輸出功率(輸出電壓曲線與X軸所圍成的面積)隨著陰陽極壓差的增大而增大。這是由于陽極壓力高于陰極壓力時，在壓差的作用下一定程度上促進了水合氫離子從陽極向陰極的遷移，加速了電荷的轉移，進而提升了電堆的輸出電壓以及輸出功率。

4.1.2 電堆溫度的影響

在研究電堆溫度對電堆輸出性能的影響時，選擇電堆溫度分別為40、60、80℃，設置陽極壓力高于陰極壓力2×104Pa。仿真結果如圖 4所示。

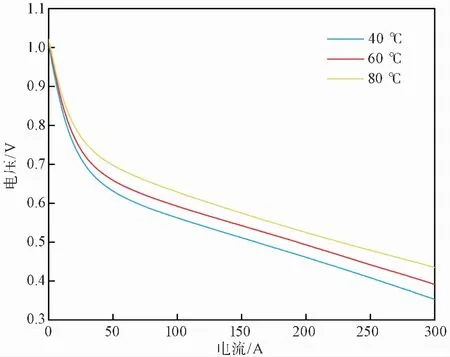
圖 4 不同溫度下輸出電壓隨負載電流的變化曲線Fig.4 Variation curve of output voltage with load current under different temperature

根據圖 4可以看出，隨著電堆溫度的升高，電池的輸出電壓逐漸升高，在相同的負載電流下，電堆的輸出功率隨溫度的升高而升高，電堆輸出電壓以及輸出功率的升高率也隨著溫度的升高而呈上升趨勢。這是由于電堆溫度升高，可以加快電化學反應中粒子的運動速度，加快氧化還原反應的進程，同時溫度的提高可以改善電堆內部加濕條件，有助于質子的遷移，進而提升電堆的輸出性能。為了滿足實際電堆的要求，電堆的工作溫度后續仿真中依然取60℃。

4.1.3 氧氣過量比的影響

在氫燃料電池系統工作過程中，氧氣過量比可以用來描述供給系統性能的優劣，是PEMFC系統工作過程中的一項重要指標。氧氣過量比即為空氣供給系統中氧氣的供給量與實際電化學反應中消耗的氧氣量的比值，可以表示為

(16)

式(16)中:λO2為氧氣過量比。氧氣過量比越大，一般情況下參與反應的氧氣越多，輸出電壓越高，但是受限于質子交換膜的有效面積，氧氣過量比較高的時候，輸出電壓的增加越來越不明顯，同時，氧氣過量比越高，空壓機的功耗越高，PEMFC系統的凈功率就受到影響。當氧氣過量比較低時(如小于1)，氧氣供應不會造成氧饑餓的現象，對燃料電池造成損傷。一般氧氣過量比在2左右比較合適。

仿真過程中，陰陽極壓力差為2×104Pa，電堆溫度為60℃恒定，負載電流分別為20、40、60、100A。在同一負載電流下，改變氧氣過量比，是為了防止發生氧饑餓現象，氧氣過量比仿真中最小為1.5，PEMFC系統的凈功率隨氧氣過量比的變化關系如圖 5所示。

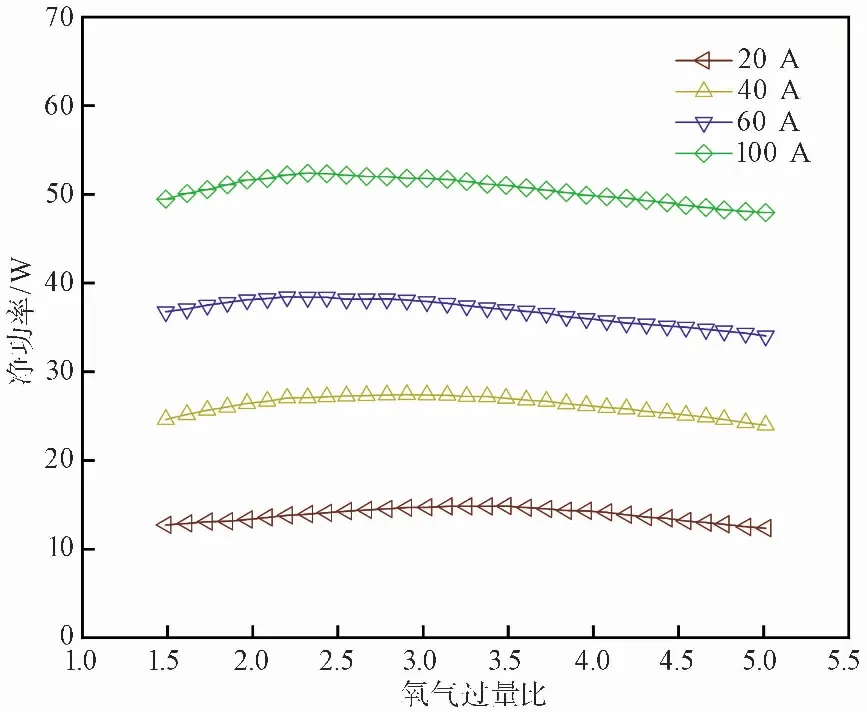
圖 5 PEMFC凈功率隨氧氣過量比的變化曲線Fig.5 Change curve of PEMFC net power with oxygen excess ratio

圖5 可以看出，PEMFC系統的凈功率隨氧氣過量比的變化而有波動，變化幅度不是很大。在同一負載電流下，凈功率隨氧氣過量比的增大均先增大后減小，主要是因為隨著氧氣過量比的增大，供氣系統主要是空壓機所消耗的能量越多，使得整體的功率下降，在該負載電流下，存在著一個最佳氧氣過量比，在此時PEMFC系統凈功率最大，且最佳氧氣過量比與負載電流相關。負載電流為20A時，最佳氧氣過量約比為3.5，負載電流為40A時，最佳氧氣過量比約為2.9，負載電流為60A時，最佳氧氣過量比約為2.3，負載電流為100A時，最佳氧氣過量比約為2.3，可以認為在高電流密度區域內(大于60A)，最佳氧氣過量比的值為2.3，而在低電流密度區域(小于60A)，最佳氧氣過量比與負載電流呈反比例函數的關系。要保證氫燃料電池堆維持最大有效功率輸出，就需要將氧氣過量比控制在該負載電流下對應的最佳氧氣過量比上。

4.2 動態性能分析

為了研究PEMFC系統的動態特性，設置電堆運行溫度為60℃，陰陽極壓差為2×104Pa，負載電流的變化如圖 6所示，在0～15s，負載電流為150A；在15～25s，負載電流為170A；在25～35s，負載電流為200A；在35～45s，負載電流為180A，在45～55s，負載電流為140A；在55～60s，負載電流為160A。氧氣過量比的值如圖 7所示，對應的電堆輸出電壓、輸出功率分別如圖 8和圖 9所示。

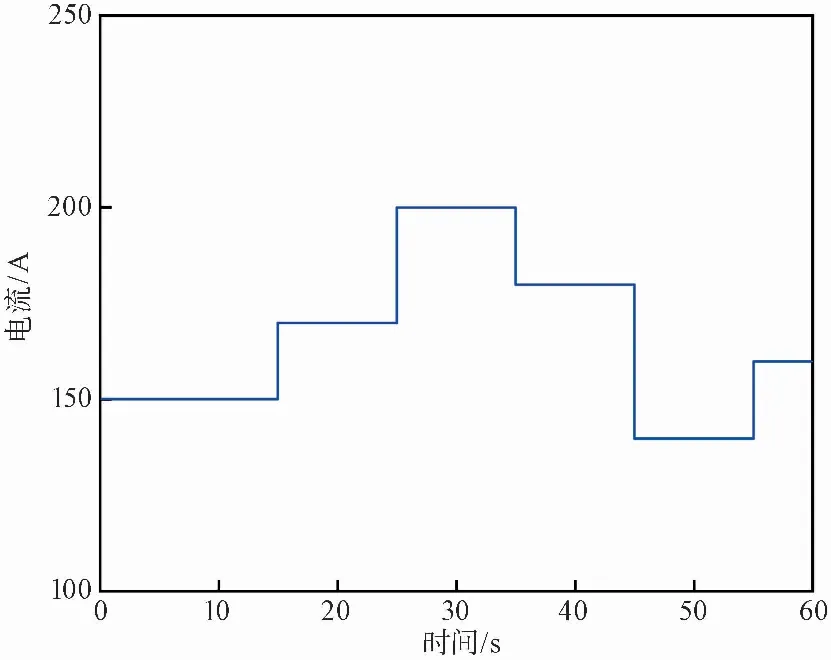
圖 6 負載電流變化曲線Fig.6 Load current curve

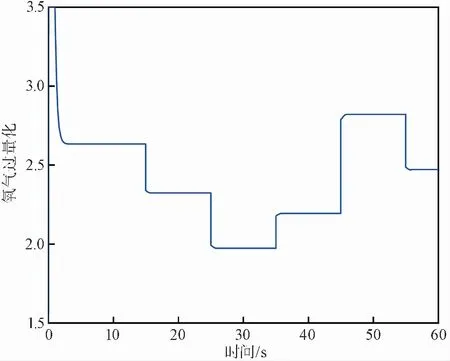
圖 7 氧氣過量比變化曲線Fig.7 Oxygen excess ratio change curve

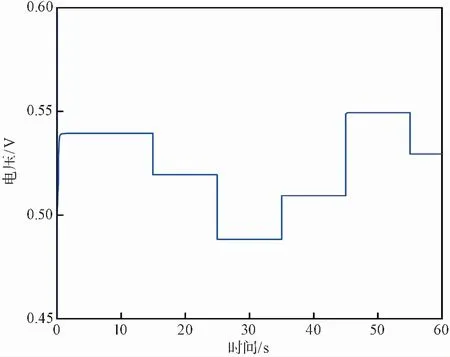
圖 8 電堆輸出電壓變化曲線Fig.8 Stack output voltage change curve

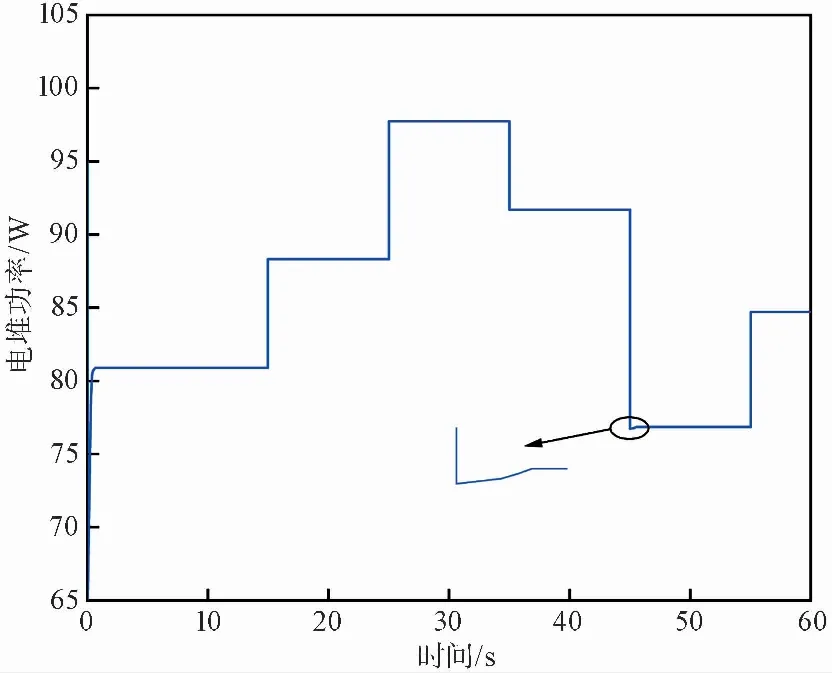
圖 9 電堆輸出功率變化曲線Fig.9 Stack output power change curve

由圖 7的仿真結果可知，負載電流變化時，氧氣過量比的大小也隨之改變，其變化規律與管路壓力以及電堆陰極壓力的變化規律類似，負載電流增大時，氧氣過量比減小，負載電流減小時，氧氣過量比增大，由于響應速度較快，響應速度與負載電流變化的關系不是很明顯。

由圖 8的仿真結果可知，負載電流變化時，電堆的輸出電壓隨之變化，輸出電壓的變化規律與氧氣過量比的變化規律完全相同。

由圖 9的仿真結果可知，負載電流變化時，電堆的輸出功率隨之變化，輸出功率的變化與負載電流的變化呈現出相同的規律，負載電流突然增大時，輸出功率比突然增大，負載電流突然減小時，輸出功率也突然減小。

由氫燃料電池系統的動態仿真結果可以看出，負載電流的變化會直接影響系統不同位置的壓力狀態，打破系統壓力的平衡點，影響電堆的輸出性能。負載電流突然增大時，由電化學反應方程式可知，在供氣量不變的情況下，系統所消耗的燃料(氧氣和氫氣)就越多，導致氧氣過量比突然下降，燃料直接消耗的環境壓力會突然下降，也就是陰極內部壓力會最先下降，而后供給管道壓力也下降，負載電流增加得越多，所消耗的氧氣就越多，供給系統就越偏離原有平衡點，在壓力差的作用下也更快地恢復到一個新的平衡點；負載電流突然增大時，導致參與反應的氣體分壓突然降低，直接影響了系統的輸出電壓，致使輸出電壓降低，盡管輸出電壓降低，但是降低的幅度相對負載電流來說比較小，系統的輸出功率整體依舊是增大。

5 結論

首先對PEMFC系統模型的描述做出合理假設，在此基礎上，搭建了PEMFC的輸出特性模型、供給管道模型以及凈功率模型，其中輸出特性模型包括輸出電壓模型、輸出功率模型以及凈功率模型，供給管道模型包括氫氣供給管道模型和空氣管道模型。此外，根據空壓機的工作特性，將空壓機看作是一個穩定的空氣源，通過調節空壓機后的電磁閥可以實現空氣流量的調節，有效地避免了空壓機帶來的不利影響，通過凈功率模型確立了電堆工作的最佳氧氣過量比，該方式大大提高了供給系統的響應速度以及響應時間。

對模型分別進行了穩態仿真和動態仿真研究。穩態仿真主要研究了PEMFC系統的陰陽極壓差、陰陽極工作壓力、電堆的工作溫度以及氧氣過量比對電池性能的影響，分析不同工況下關鍵參數對電池的影響規律；動態仿真為負載電流突變時，得到工況突變時電池的輸出性能隨時間的變化關系曲線圖，分析PEMFC系統進氣特性和輸出特性的動態響應。根據仿真結果，得出結論如下。

(1)電堆的工作壓力、溫度、壓力差的升高對電堆的輸出性能有積極的影響。

(2)氧氣過量比的適當增大可以提高電堆的輸出性能，但氧氣過量比過大時，則會降低氫燃料電池系統的凈功率。

搭建的燃料電池模型同樣適用于研究不同參數指標的燃料電池系統，具有一定的普適性。根據仿真分析結果確定部分仿真研究的工作參數，為接下來系統控制目標的提出、控制策略的制訂奠定了基礎。