季節(jié)性凍土區(qū)黏土凍結深度預測

周元輔，張丹鋒，李明勇，索曉慶，張學富

(重慶交通大學土木工程學院山區(qū)橋梁及隧道工程國家重點實驗室，重慶 400074)

季節(jié)性凍土的凍脹對路基、邊坡、隧道等基礎設施的安全和耐久性極其不利。中國相關規(guī)范[1-4]都涉及了凍結深度，由此可見凍結深度在季節(jié)性凍土區(qū)工程建設的重要性。影響季節(jié)性凍土凍結深度的因素很多，從空間來看，季節(jié)性凍土的凍結深度與海拔、緯度密切相關[5-6]，這是因為不同海拔和緯度地區(qū)的氣溫和地溫不同[5，7]。在凍結深度預測計算中，凍結深度與凍結負溫、凍結時間、積溫等氣溫參數(shù)[8-10]直接相關。土的性質、含水量、輻射、植被、積雪等是影響凍結深度的關鍵因素[8，11-14]。凍結深度是季節(jié)性凍土區(qū)工程建設中防凍脹設計的關鍵參數(shù)之一，大量學者開展了凍結深度預測研究。由于凍結深度的影響因素眾多，這些年凍結深度預測研究持續(xù)不斷。其中公認度較高的預測公式是基于傳熱學理論的Stephan公式或在此基礎上改進的公式[15-16]。中國經(jīng)過多年工程實踐和經(jīng)驗總結，綜合考慮了土體類別、凍脹性、環(huán)境、地形等因素之后，《建筑地基基礎設計規(guī)范》[1]、《凍土地區(qū)建筑地基基礎設計規(guī)范》[2]、《凍土工程地質勘察規(guī)范》[3]等規(guī)范給出了凍結深度計算公式，但是這些公式?jīng)]有考慮凍土的含水率或含水量。由《凍土工程地質勘察規(guī)范》[3]可知，黏性土的凍脹性較強，且含水量對其凍脹性影響顯著。然而，現(xiàn)行規(guī)范中無針對季節(jié)性凍土區(qū)黏性土且考慮含水影響的凍結深度計算公式。基于此，開展考慮含水率的季節(jié)性凍土區(qū)黏性土凍結深度預測意義重大。

中國季節(jié)性凍土分布廣泛，為了保障試驗溫度邊界條件具有季節(jié)性凍土區(qū)的典型環(huán)境溫度特征，現(xiàn)統(tǒng)計中國黑龍江省、吉林省、遼寧省、內(nèi)蒙古自治區(qū)、新疆維吾爾自治區(qū)等季節(jié)性凍土地區(qū)氣溫，獲得這些地區(qū)的氣溫特征，以此為溫度邊界條件。為了獲得考慮土體含水率的黏性土凍結深度預測公式，開展了10%(試樣1)、20%(試樣2)、30%(試樣3)3個不同初始質量含水量的單向凍融試驗，基于試驗結果分析經(jīng)驗公式預測誤差和體積含水量的關系，建立更加準確的預測公式，為季節(jié)性凍土區(qū)內(nèi)的黏土地區(qū)基礎設施建設提供參考。

1 溫度邊界條件與試驗準備

1.1 溫度邊界條件

季節(jié)性凍土在中國北方分布廣泛，例如東北、西北和華北。黑龍江省的地表土層基本從10月開始凍結，持續(xù)到下一年3月或4月達最大凍結深度[17]。北疆地區(qū)季節(jié)性凍土在每年的10月下旬或11月上中旬開始凍結，第二年的2月底或3月初凍結深度達到最大值[18]。基于高焱等[19]調(diào)研的全國常見季節(jié)性凍土區(qū)，通過查詢天氣后報，獲得了黑龍江省、吉林省、遼寧省、內(nèi)蒙古自治區(qū)、新疆維吾爾自治區(qū)等季節(jié)性凍土地區(qū)1年的氣溫。首先統(tǒng)計了每月的最低溫度和最高溫度，然后將一年12個月的最低溫度和最高溫度取算術平均得到圖 1中的最低溫平均值(-21.5℃)和最高溫平均值(29.5℃)。基于此統(tǒng)計結果，本次試驗的溫度邊界條件設為T=25cos(πt/12)，一個試驗周期內(nèi)試驗環(huán)境溫度隨試驗時間變化如圖 2所示。試驗溫度由試驗環(huán)境箱的控制系統(tǒng)控制，試驗中1h為一個時間增量，在1h內(nèi)設定為一恒定溫度，溫度和時間的對應關系由圖 2中的公式確定。試驗總時間為7個周期，每個周期24h。試驗中2h模擬現(xiàn)實中的1個月，24h模擬1年時間。時間相似比為1︰360，根據(jù)時間相似比得到幾何相似比為 1︰18.97。

1.2 試驗準備

通過TYS-3型土體液塑限聯(lián)合測定儀測得本實驗土的塑性指數(shù)Ip=13.2，且篩分結果表明粒徑大于0.075的顆粒質量小于總質量的50%，根據(jù)《公路工程地質勘察規(guī)范》(JTGC20—2011)[20]的規(guī)定，實驗用土為粉質黏土。試驗制備了10%(試樣1)、20%(試樣2)、30%(試樣3)3個不同初始質量含水量的試樣。試驗土柱試樣直徑為20cm，高度為60cm。為了保障試樣在試驗過程中處于單向凍融，試件周圍以及底部鋪設10cm厚隔熱層，頂部與環(huán)境箱內(nèi)的空氣接觸。試驗時將3個試樣同時放在同一環(huán)境箱中開展試驗。在布置傳感器之前，通過數(shù)值分析獲得了第七周期內(nèi)邊界溫度為最低溫度和最高溫度時，土體試樣中心的溫度分布(圖 3)。由圖 3 可知，距試樣頂端越近土體溫度變化越復雜，距試樣頂端越遠土體溫度變化越小且趨于一致。因而溫度及水分傳感器在底部布置稀疏而頂部比較密集。每個試樣布置11個溫度傳感器和6個水分傳感器。溫度傳感器從下到上編號依次為T-1～T-11，水分傳感器從下到上編號依次為W-1～W-6，溫度與水分傳感器的布置如圖 4所示。溫度傳感器為中國科學院寒區(qū)旱區(qū)環(huán)境與工程研究所研發(fā)的M51型熱敏電阻式溫度傳感器，其量程為-40～50℃，精度為±0.01℃。水分傳感器為EC-5土體水分傳感器，其量程為0～100%，分辨率0.1%，精度±3%。EC-5土體水分傳感器所測含水率為未凍水的體積含水率。

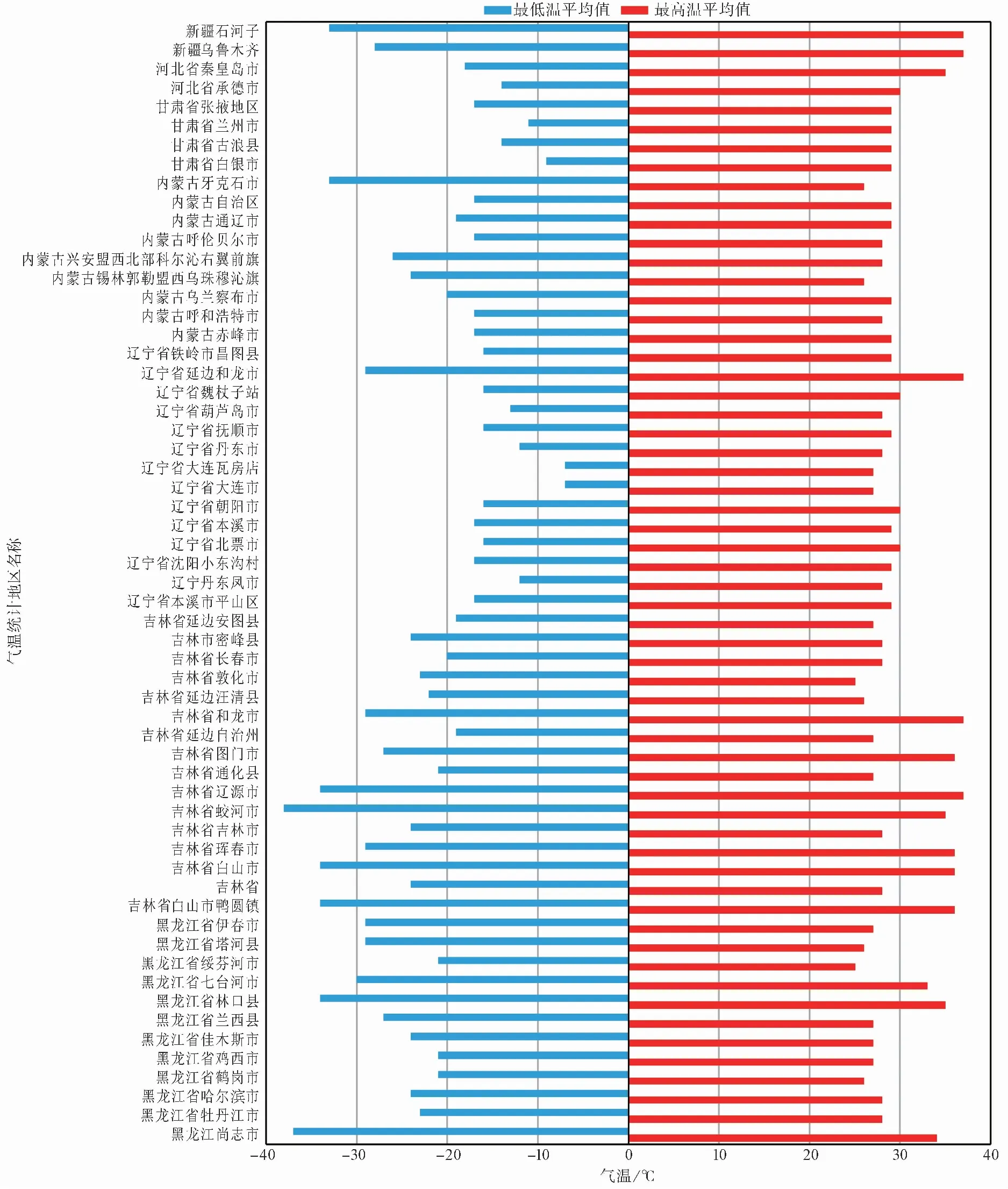
圖 1 中國部分季節(jié)性凍土區(qū)的 每月最高溫和最低溫平均值Fig.1 The average of monthly maximum and minimum temperatures in some seasonally frozen regions of China

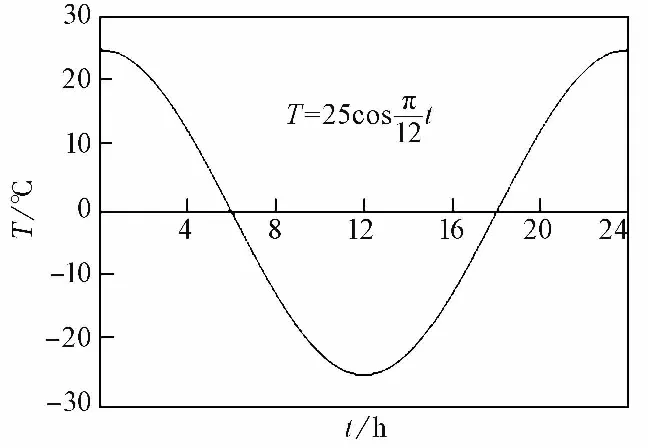
圖 2 單個試驗周期內(nèi)環(huán)境溫度隨時間變化Fig.2 Environmental temperature varied with time during a test period

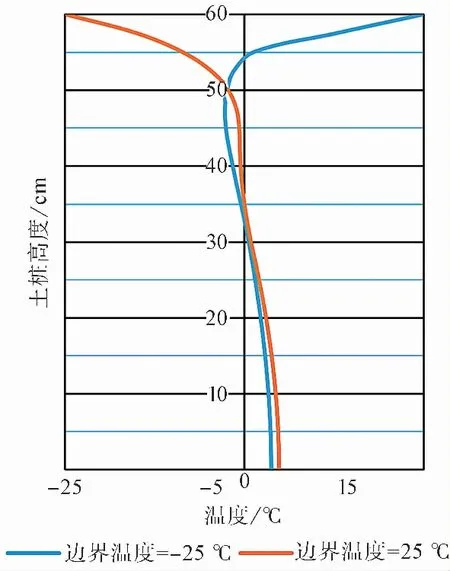
圖 3 數(shù)值模擬試樣溫度分布Fig.3 The temperature distribution of sample based on numerical simulation

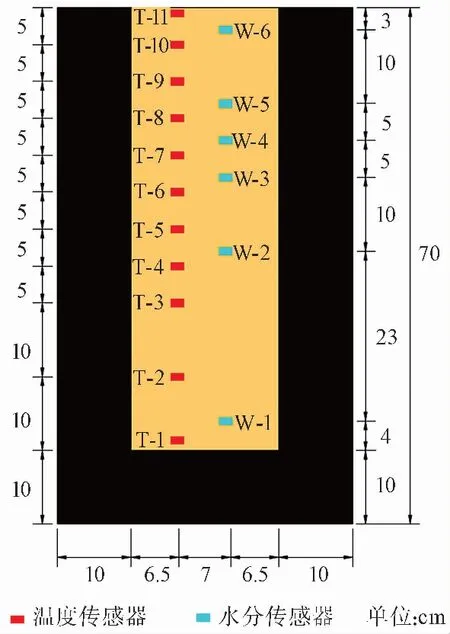
圖 4 傳感器布置圖Fig.4 Sensors distribution

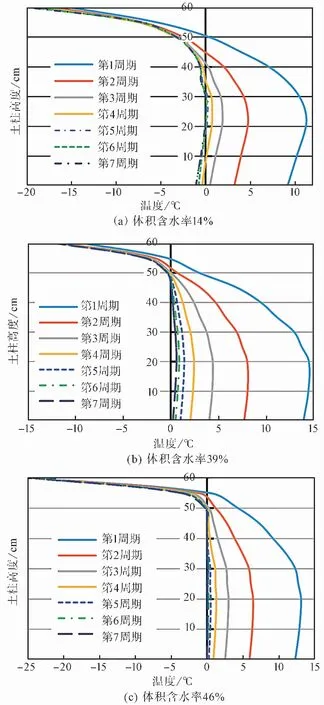
圖 5 各測點最低溫度隨凍融周期變化Fig.5 Minimum temperatures of all sensors varied with freezing-thawing cycles

2 試驗結果分析

2.1 各測點最低溫度

不同試樣中的各測點在每個試驗周期內(nèi)的最低溫度各不相同(圖 5)，但是各測點在單個周期內(nèi)的最低溫度都隨周期的增加逐漸降低。各測點在第1周期的最低溫度與第2周期最低溫度的差值最大，試樣1的最大差值為6.51℃，試樣2的最大差值為6.45℃，試樣3的最大差值為6.68℃。每個試樣的各測點在第6周期的最低溫度與第7周期最低溫度的差值最小，試樣1的最大差值為0.39℃，試樣2的最大差值為0.28℃，試樣3的最大差值為0.13℃。由此可見，在7個試驗周期之后，各測點的最低溫度與第6周期的差值都小于0.4℃。因而，此時土體溫度分布趨于穩(wěn)定。

2.2 各測點未凍水體積含水率變化量

每個水分測點在一個周期內(nèi)所測的未凍水體積含水率變化量(最大值與最小值之差)能夠在一定程度上反映測點周圍土體的含水率變化情況，各測點的未凍水體積含水率變化量在每個試驗周期中的變化如圖 6所示。測點W-1～W-4的體積含水率變化量在第1周期最大，在第2周期之后基本不變，且試樣1的含水率變化量小于1.5%，試樣2和試樣3小于2.0%。由此可見，測點W-1～W-4在第2周期后未凍水體積含水率變化較小，未凍水體積含水率趨于穩(wěn)定。

2.3 最大凍結深度

從一個周期內(nèi)各溫度測點最低溫度和各水分測點未凍水體積含水率變化量可知，模型試驗運行7個周期能夠模擬自然狀態(tài)下季節(jié)性凍土區(qū)內(nèi)黏土的凍結狀態(tài)。基于第7周期試驗結果，首先獲得試樣最低負溫測點，再查找相鄰正溫測點，獲得該測點溫度為最低溫時沿試樣高度的溫度分布(圖 7)，最后以0℃作為凍結線，線性插值獲得最大凍結深度。試樣1 的最大凍結深度為28cm，試樣2的最大凍結深度為15cm，試樣3的最大凍結深度為12cm。由試驗相似比得到自然狀態(tài)中的最大凍結深度：試樣1的最大凍結深度為5.3m，試樣2的最大凍結深度為2.8m，試樣3的最大凍結深度為2.3m。雖然試樣2 和試樣3 的最大凍結深度接近，但是從土體溫度分布可以看出，土體的含水量越大其整體溫度越低。

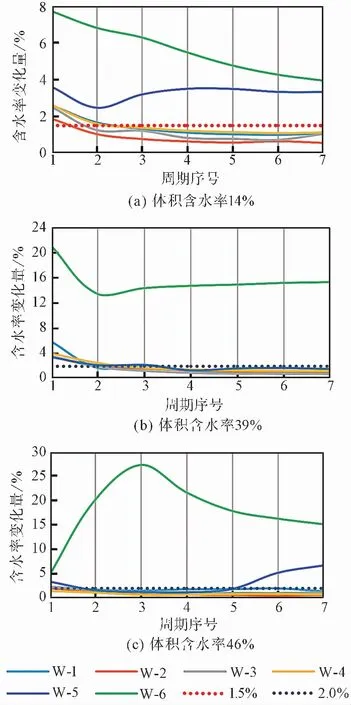
圖 6 一個周期內(nèi)未凍水體積含水率變化量隨凍融次數(shù)變化Fig.6 Volumetric moisture content variation of unfrozen water changed with freezing-thawing cycles in a period

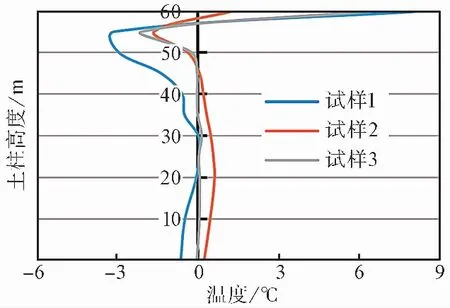
圖 7 第7周期各試樣的最大凍結深度Fig.7 Maximum freezing depth of each sample in the 7 period

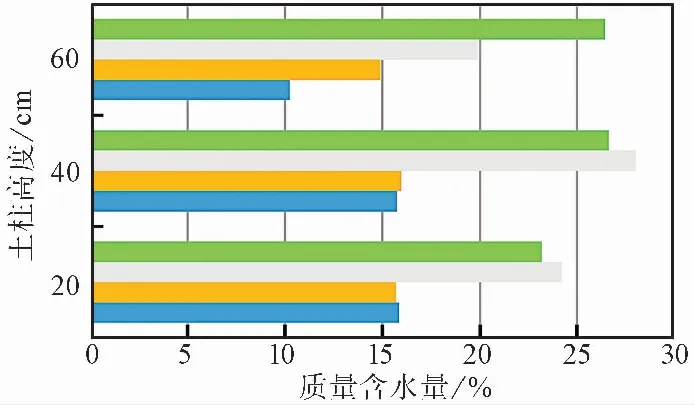
圖 8 不同部位質量含水量Fig.8 Mass water content of different sections

3 凍結深度預測研究

3.1 試驗凍結深度預測

目前，工程實踐中最常用的凍結深度計算公式是Stephan公式或其改進公式，中國相關規(guī)范也給出了凍結深度計算公式(表 1)。

通過室內(nèi)試驗和相關規(guī)范查詢得到凍結深度計算的相關參數(shù)(表 2)，結合Stephan公式、魯基揚諾夫公式、《建筑地基基礎設計規(guī)范》公式、《凍土地區(qū)建筑地基基礎設計規(guī)范》與《凍土工程地質勘察規(guī)范》公式，得到本試驗的凍結深度預測值(表 3)。

由表 3可知，Stephan公式與魯基揚諾夫公式計算的凍結深度隨土體含水量的變化，而由規(guī)范獲得的凍結深度都是1.98m。從預測值的誤差可以看出，3個試樣由魯基揚諾夫公式計算的凍結深度誤差都在20%～30%，由Stephan公式預測的試樣1和試樣2的凍結深度誤差小于15%，但是試樣3的誤差接近50%。由規(guī)范公式預測的試樣1的凍結深度誤差大于60%，試樣3的誤差小于15%，試樣2的誤差與魯基揚諾夫公式相同。Stephan公式預測值的平均誤差為21.8%，魯基揚諾夫公式預測值的平均誤差為26.4%，規(guī)范計算值的平均誤差為35.3%。雖然魯基揚諾夫公式預測值的平均誤差大于Stephan公式預測值，但是其均勻性較好，因而魯基揚諾夫公式優(yōu)于其他3個公式。

表 1 凍結深度計算公式Table1 Calculation formula of freezing depth

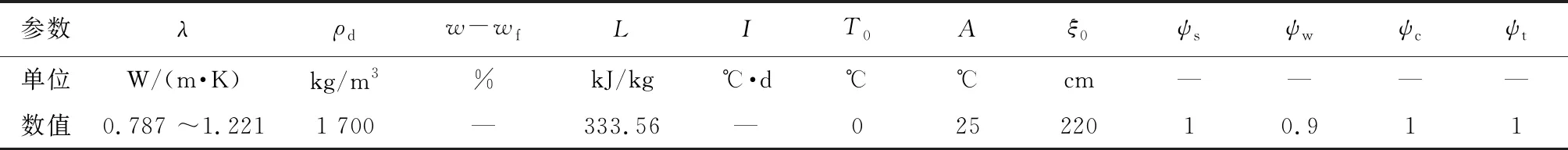
表 2 凍結深度計算參數(shù)

表 3 試驗凍結深度實測值和預測值

3.2 凍結深度預測修正

上述研究表明規(guī)范對含水量較小的土體凍結深度計算值的誤差較大，因而通過分析誤差和含水量的關系，建立了基于《凍土地區(qū)建筑地基基礎設計規(guī)范》計算的凍結深度的修正公式為

(1)

(2)

式中：Z0為修正后的凍結深度，m；ξk由《凍土地區(qū)建筑地基基礎設計規(guī)范》計算公式獲得的凍結深度，m；wV為初始未凍水體積含水率；wg為初始質量含水量。

由式(1)修正《凍土地區(qū)建筑地基基礎設計規(guī)范》計算值后，試樣1、試樣2和試樣3的凍結深度誤差分別為4.9%、2.0%、5.8%。由式(2)修正《凍土地區(qū)建筑地基基礎設計規(guī)范》計算值后，試樣1、試樣2和試樣3的凍結深度誤差分別為12.8%、10.0%、0.4%。由此可見，式(1)修正后的凍結深度更為準確和可靠，在實際應用過程中建議優(yōu)先使用式(1)。

4 討論

為了檢驗水分傳感器在試樣平面上布置的合理性，在本試驗完成后分別在試樣1和試樣2的20、40、60cm 3個平面的中心和側壁處取樣并采用烘干法獲得質量含水量(圖 8)。從測試結果來看，試樣1 和試樣2 在20cm和40cm處平面的中心含水量和側壁含水量僅相差1%。試樣頂面由于受到環(huán)境空氣和模具的影響，中心含水量與側壁含水量差別較大。因而，在直徑為20cm的試樣頂部以下的任一平面的任一位置布置水分傳感器的測試結果都比較可靠。

5 結論

通過開展室內(nèi)試驗和凍結深度預測與修正研究，得到以下結論。

(1)以中國部分季節(jié)性凍土地區(qū)氣溫特征為基礎，設計了年平均溫度為0℃，振幅為25℃的溫度邊界，開展了10%、20%、30% 3種不同初始質量含水量的單向凍融試驗，獲得了它們的最大凍結深度分別為5.3、2.8、2.3m。

(2)通過對比分析預測值和實測值表明，Stephan公式預測值的平均誤差為21.8%，魯基揚諾夫公式預測值的平均誤差為26.4%，相關規(guī)范計算值的平均誤差為35.3%，其中魯基揚諾夫公式預測的凍結深度相對其他公式較準確。

(3)利用初始未凍水體積含水率修正基于《凍土地區(qū)建筑地基基礎設計規(guī)范》的凍結深度計算值，誤差在6%之內(nèi)，在季節(jié)性凍土區(qū)的黏土地區(qū)建議用該修正公式計算凍結深度作為設計凍結深度。