基于小波神經網絡對鐵路客運量的預測研究

張 鵬，唐琴琴

（太原工業學院理學系，山西太原 030008）

鐵路客運是我們生活中必不可少的一部分，預測研究鐵路客運量是很有必要的，首先，我國資源豐富，但分布不均衡，而鐵路客運這種交通方式不僅便捷，而且效率高；其次，近年來，人們在衣食住行方面的要求越來越高，需要對鐵路客運進行準確地預測；最后，如果對鐵路客運預測的不準確，這將導致決策者的方案失效，不利于鐵路客運的發展，因此需要對鐵路客運做出準確的預測。

主要研究小波神經網絡模型，并預測鐵路客運量。首先，將統計年鑒中的數據分為訓練樣本以及預測樣本；其次，針對數據進行去噪處理是為了提升序列的光滑度，通過相空間重構[1]確定神經網絡的輸入層節點數，根據經驗公式以及對比仿真實驗確定隱含層節點數，隱含層函數選取小波基函數；最后，利用預測樣本得到的結果與原始數據對比[2]。

1 小波神經網絡

1.1 小波去噪

小波去噪是在原始信號的基礎上，完成對原信號s(t)與噪聲信號n(t)的區分，

其中n(t)服從的分布為正態分布n(t)～N(0,σ2)。

小波閾值除噪，起初需要指定一個界限值λ，該值也稱為閾值，對閾值來說，能夠將其劃分為整體界限值以及部分界限值。進行小波變換以后，會得到小波分解系數wj,k，如果臨界值大于小波系數，認為此系數因噪聲形成，可將其刪除；如果大于λ，可把原因歸咎于信號，可引用此部分，進行重新構造得到結果。

1.2 相空間重構技術理論

相空間重構有兩個關鍵的參數：嵌入維數m 和延遲時間τ，C -C 平均法對τ,w 的選取更可靠。設時間序列x={xi|i=1,2,…,N |}重構后，有新的序列X=，記X={Xi}，為相空間中的點。嵌入時間序列關聯積分表示相空間中任意兩點之間距離小于r的概率：

其中dij=‖ xi-xj‖(∞)表示點與點之間距離為矢量之差的無窮范數，θ(·)為Heaviside函數。檢驗統計量：S1(m,N,r,t)=C(m,N,r,t)-Cm(1,N,r,t)，定義差量為：

1.3 神經網絡原理

神經網絡由輸入層，隱含層和輸出層組成。層與層之間權值不相同，通過信號的正向傳遞與誤差的反向傳遞[3]實現，設輸入層為xi，隱含層為yj，輸出層為zl，實際輸出為tl，第i輸入層與第j隱含層之間權值為wij，第j 隱含層與第l 輸出層之間權值為vjl，θj為隱含層的閾值，θl為輸出層的閾值。

第j隱含層值為：

第l輸出層值為：

輸出層與實際值的誤差：

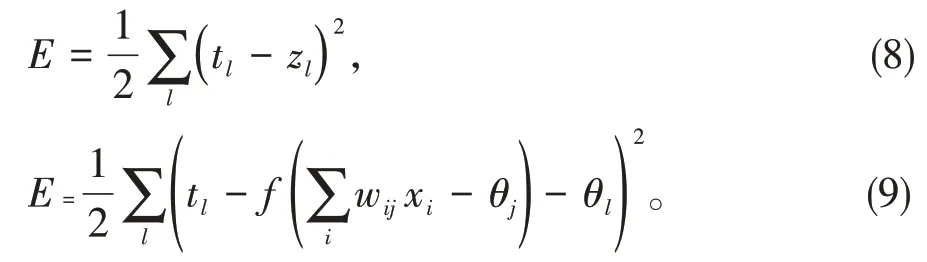
1.4 數據預處理

在對原始數據進行統計分析時，通常情況下，需要處理原始數據，對數據進行歸一化[4]處理：

輸出時對數據進行反歸一化處理：

1.5 小波神經網絡模型的構造

構造小波神經網絡[5]時，隱含層函數需要采用小波基函數，根據經驗，選擇收斂的，區間內是單調遞增的函數[6]，平移因子，伸縮因子代替層與層之間的權值以及閾值。

網絡輸入為x1,x2,…,xn，輸出為yi，小波神經網絡層與層之間權值分別為wij，wjl，輸入信號為xi(1,2,…,k)，隱含層節點數由經驗公式求得。

2 實證分析

2.1 提取實驗數據

選取自國家統計局的鐵路客運量月度數據，如圖1所示。可知，原始數據有指數趨勢[5]，且具有周期性，取前150個數據為訓練集，剩下的為預測集，對數據進行擬合以及預測。

圖1 原始數據圖像

2.2 小波去噪

首先對數據進行去噪處理，原始時間序列可以小波分解為：

如圖2為去噪后的信號：

圖2 去噪后數據

選擇小波基函數為db6，分解層數為3。對原始數據進行去噪，去除噪聲系數，去噪后圖像相較于原始數據來說是光滑的，更有利于處理數據。

2.3 輸入層節點數的確定

利用相空間重構處理去趨勢數據，可以得出時間延遲為4，時間窗為3，因此嵌入維數為2，即小波神經網絡的輸入層節點數為2，將重構后的數據代入模型。

去趨勢處理后的數據只含有周期性因素，沒有指數趨勢，有利于對原始數據相空間重構，求取時間延遲與時間窗，由圖3 可得輸入層的各個參數，將重構后的數據代入模型。

圖3 去趨勢處理

取時間延遲的范圍為1～50，如圖4為時間延遲以及時間窗圖像。

圖4 在t 為4 時取極小值點，因此取圖像的極小值點4，即為延遲時間。圖5 在t為3 時，取最小值，圖像的最小值對應時間為時間窗，時間窗為3。

圖4 時間延遲

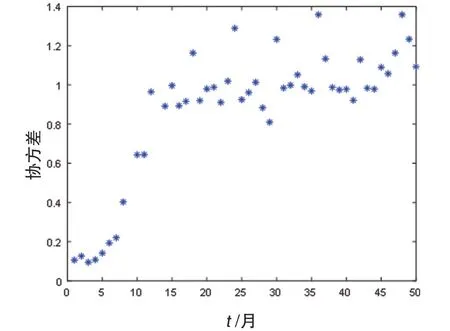
圖5 時間窗

2.4 隱含層節點數的確定

通過對比仿真實驗來確定小波神經網絡的隱含層節點數，由經驗公式可得：

a 為的常數，M,N 分別為輸入層，輸出層的節點數.通過仿真對比實驗，隱含層數定為7。

2.5 對鐵路客運量的預測研究

2.5.1 對原始數據分析

由相空間重構可得，輸入層節點數為2，隱含層節點數為7，取隱含層函數為帽函數[7]的時候，網絡模型最佳，可得到原始數據的訓練集與其擬合值的對比圖像以及預測集對比圖像，如圖6所示。

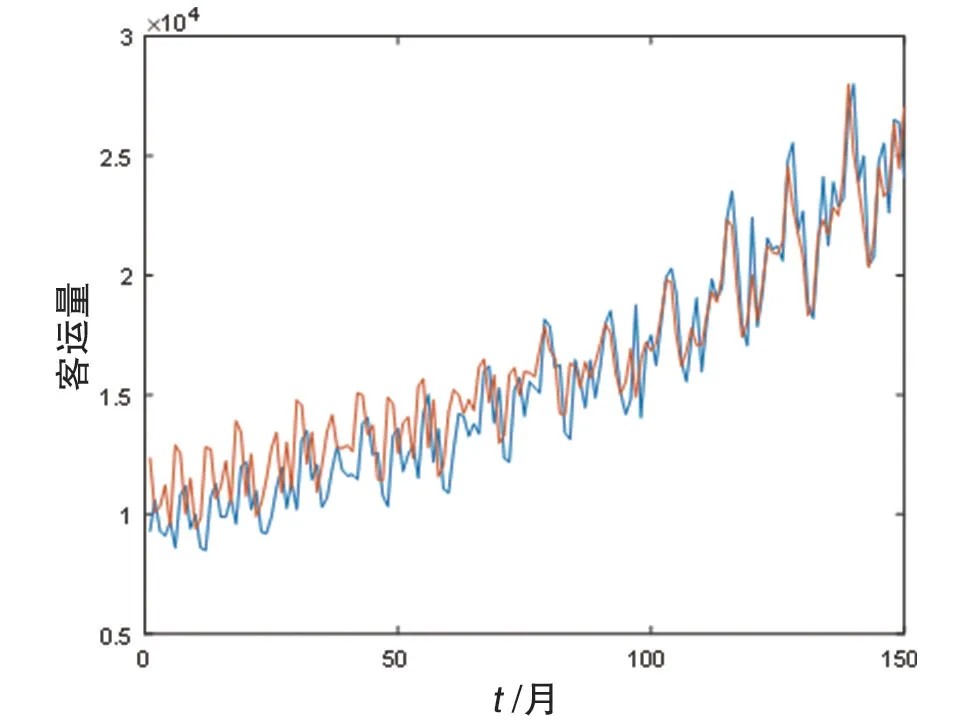
圖6 原始數據與擬合值對比圖

由圖7 可知，誤差相對很大，尤其是預測樣本數據的波動性很大，所以預測效果不樂觀。如圖7所示為原始數據的每一個值與擬合值得到的誤差圖像,預測效果誤差很大，其原因與原始數據的不光滑有關。

圖7 預測值圖像

2.5.2 小波去噪后分析

當進行小波去噪后，建立網絡模型，如圖8 所示為去噪后的數據與擬合值的對比圖像以及預測集實際值與擬合值圖像。

由圖8可知，原始數據去噪后，數據較為光滑，擬合值幾乎和原始數據去噪后的數據完全重合，網絡模型誤差小。對預測樣本進行預測時，大部分點幾乎是重合的，因此對原始數據進行去噪處理后，小波神經網絡模擬效果較好。

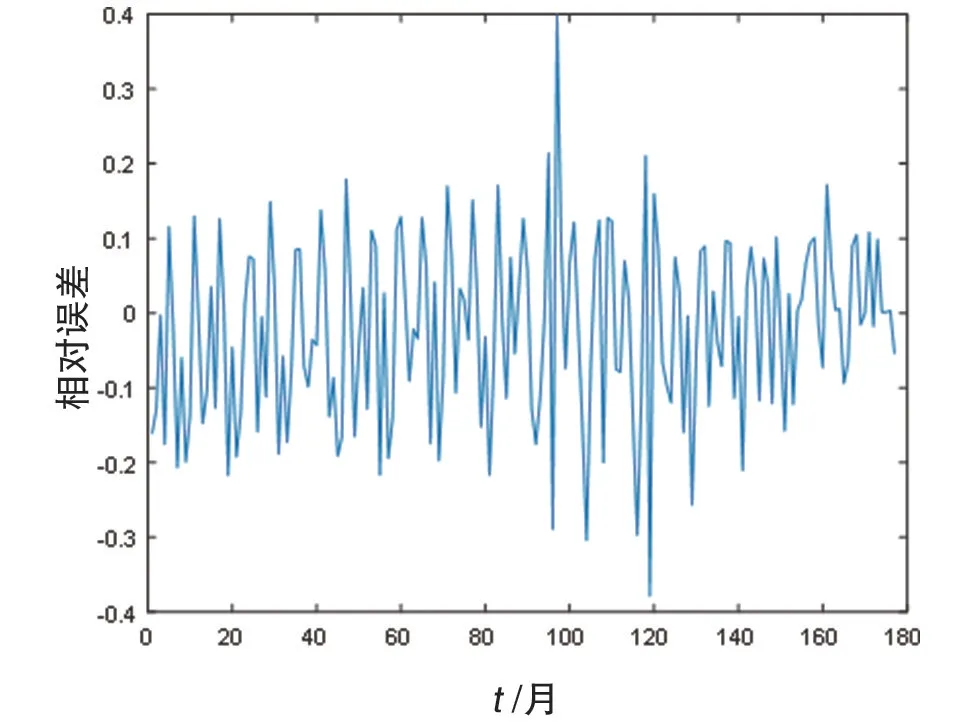
圖8 神經網絡誤差圖

如圖9所示為每個點的誤差圖像，與未去噪的相比，誤差很小。

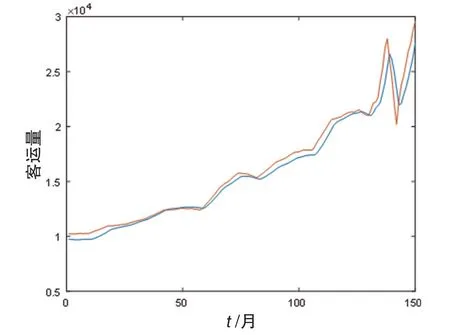
圖9 去噪后數據與擬合值圖像

由圖9～11可知，對原始數據進行去噪后，預測集的實際值與小波神經網絡的擬合值誤差相對很小，預測效果好。

圖10 預測實際值與擬合值圖像

圖11 預測實際值與擬合值誤差

3 結論

利用小波神經網絡對鐵路客運量進行了預測研究，首先，對原始一維數據進行相空間重構，得到二維數據，其次計算隱含層節點數，最后進行小波神經網絡的構建，隱含層函數選取小波函數，層與層之間的權值隨機設定，將原始數據與去噪后的數據的實際值，擬合值作比較，去噪后的效果更好，但本論文數據量不大，因此需要擴大樣本容量，會使網絡模型更好.對小波函數的選擇可利用數值法求解，如若用對比仿真實驗，雖然簡單，但模擬量較大。