基于層次分析法的路線規劃算法的建模與仿真

楊曉敏，李梓涵

（運城學院數學與信息技術學院，山西運城 044000）

隨著經濟和社會的發展，人們對休閑娛樂的要求越來越高，大型游樂場成為了人們休閑娛樂的一個重要場所。人們在大型游樂場游玩時經常會面臨著一些選擇：游玩時如何選擇游玩順序才能省時又盡興？而對于游樂場來說，同樣需要考慮如何才能使游客有好的游玩體驗的同時獲得更高的收益。

游樂場內部項目的游玩規則分為兩種：需要預約的和隨時可以游玩的，需要預約的為項目A1～A11，隨時都可以游玩的項目為B1～B27。購買通票和購買門票的游客都可以游玩A系列項目和B系列項目。該游樂場售票采用現場售票和網上售票兩種，網上的票價以所規定票價的9 折出售，現場售票在每天的早上8:00開始。游客8:30開始入場，9:00整各個項目開始開放。下午結束的時間分為兩種，冬季作息時間，室外游樂場項目17:30 結束，室內游樂場19:00 結束；夏季作息時間，室外游樂場19:00 結束，室內游樂場20:00結束。

針對某個大型游樂場的部分運營數據,預測未來游客的數量。某游客計劃在2019 年8 月5 日到該游樂場購買通票游玩，通過對歷史數據進行建模，找到最優的游玩順序。

1 問題分析

項目游玩人數預測問題，需要根據歷史數據來預測未來的數據據，首先分析了各個項目游玩人數和當天游客人數的關系，得出基于線性回歸的預測模型[1-4]，參考排隊論[5-8]，計算了8 月5 日的每個項目的排隊人數和排隊時間。通過對當天人數的預測，進一步進行游玩路線的規劃。針對需要解決的問題，建立游樂場游客預測及路線規劃模型結構示意圖如圖1。

圖1 游樂場游客預測及路線規劃模型結構圖

首先進行數據的預處理，主要是對數據進行了數據的質量分析、缺失值和異常值的刪除；分析了各個項目游玩人數和當天游客人數的關系，得出基于線性回歸的預測模型，參考排隊論，計算了8 月5 日的每個項目的評價排隊人數和排隊時間；最后將游玩順序問題分為三個部分，分別為項目評價、項目選擇、游玩順序確定。首先根據項目的特征如人數、收費、等待時間等建立了基于層次分析法[9-10]的項目顧客滿意度評價模型；進一步地根據上述提供的滿意度最大化作為優化目標，游玩時間作為限制條件建立了基于多元線性規劃的項目選擇模型，得出最大滿意度的項目選擇；最后定義了項目游玩的平衡指標，將上述項目選擇結果建立相關的圖論模型通過遺傳算法得出類旅行商的具體游玩順序，由此確定了游客路線規劃模型并得到其價格的評估模型。

2 游樂場游客預測及路線規劃模型的建立與求解

2.1 數據預處理

因為數據存在著許多臟數據，缺省數值。使用這些未經處理過的數據在一定程度上會對模型的建立過程中帶來很多不必要的麻煩，對模型的輸出也會造成極大的干擾作用，甚至還會得到錯誤得結果。所以，應在模型建立之前對數據進行合理，適當的預處理。主要針對其缺失值進行去除處理，然后在針對其不在其正常范圍區間的值進行去除，并對異常數據進行了處理。

2.2 基于多無線性回歸的項目游玩人數預測模型

項目游玩人數預測問題，分析了各個項目游玩人數和當天游客人數的關系，得出基于線性回歸的預測模型。具體過程如下，通過已有的數據，建立多元線性回歸的預測模型。首先在數學關系先假設存在的線性關系：

根據線性回歸方法，編程預測出在2019 年8 月5日A4，B5，B12，B25 四個項目當天的游玩人數分別是9 746，9 302，354，8 922。

2.3 參考排隊論理論

可以得到平均排隊隊伍長度為：

由此可以得到其各個項目的排隊隊伍長和排隊時長見表1。

表1 各個項目的排隊人數和時長結果

3 基于層次分析法的項目顧客滿意度評價模型

層次分析法是一種定性與定量相結合的系統分析法，根據問題的總目標，以系統化的觀點，把問題分解成若干因素，并按其支配關系構成的遞階層次結構模型，然后運用兩兩比較的方法確定決策方案的重要性，從而獲得滿意的決策。

3.1 構造層次結構圖

人們選擇游玩項目時主要考慮項目的時間效率、項目吸引力、項目的可玩性等三方面的性能，將決策的目標、考慮的因素（決策準則）和決策對象按它們之間的相互關系分為最高層、中間層和最低層，繪出層次結構如圖2。

圖2 層次分析結構示意圖

3.2 構造對比矩陣

在確定各層次各因素之間的權重時，如果只是定性的結果，則常常不易被別人接受，因而采用了Santy 等人提出的一致矩陣法，即不把所有因素放在一起比較，而是兩兩相互比較，此時采用相對尺度，盡可能減少性質不同的諸因素相互比較的困難，以提高準確度。

判斷矩陣是表示本層所有因素針對上一層某一個因素的相對重要性的比較。判斷矩陣的元素用Santy 的1～9 標度方法給出。通常用1～9 及其倒數作為程度比較標準，即九級標度法見表2。

表2 九級標度法含義表

根據上述程度比較表格，得到各個層次的對比矩陣。

A層對目標層的對比矩陣：

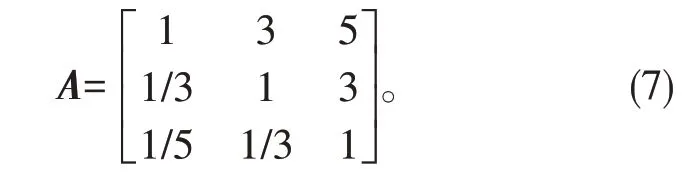
B層對A層的對比矩陣：

C層對B層的對比矩陣：

3.3 進行一致性檢驗并計算權向量

在得到相關對比矩陣之后，需要確保其中各個賦值整體的一致性，所以進行了一致性檢驗，其中一致性指標其具體：

一致性檢驗需要滿足：

其中隨機一致性指標RI與n有關，具體數值見表3。

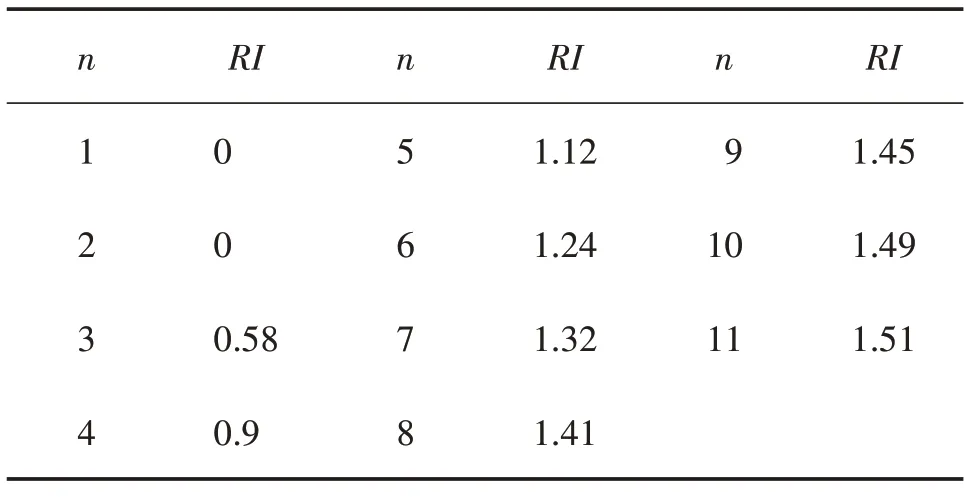
表3 RI數值參考表格

根據上述計算公式，得到各個對比矩陣一致性檢驗結果見表4。

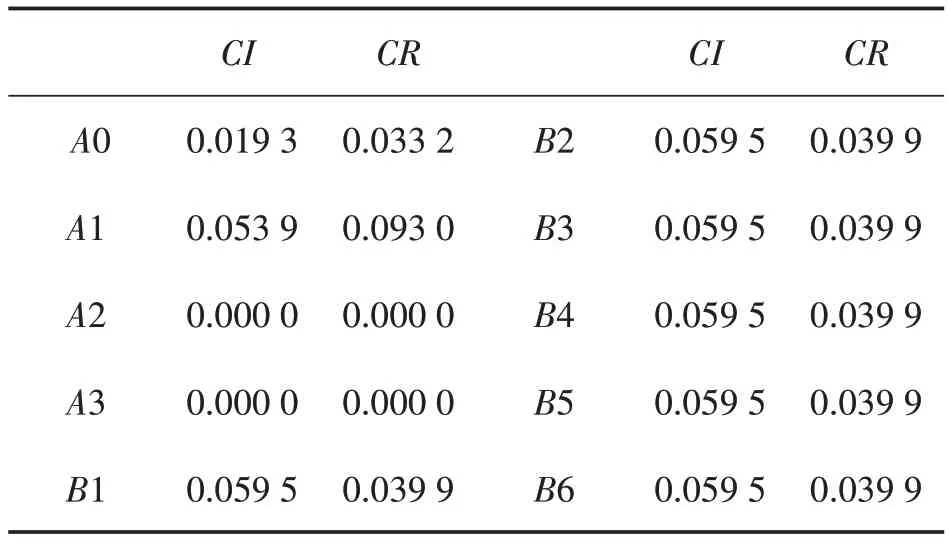
表4 一致性檢驗結果

從上表中可以看到各個對比矩陣一致性檢驗均滿足要求，根據上述模型最后得到的游客對各個項目的的喜愛程度見表5。

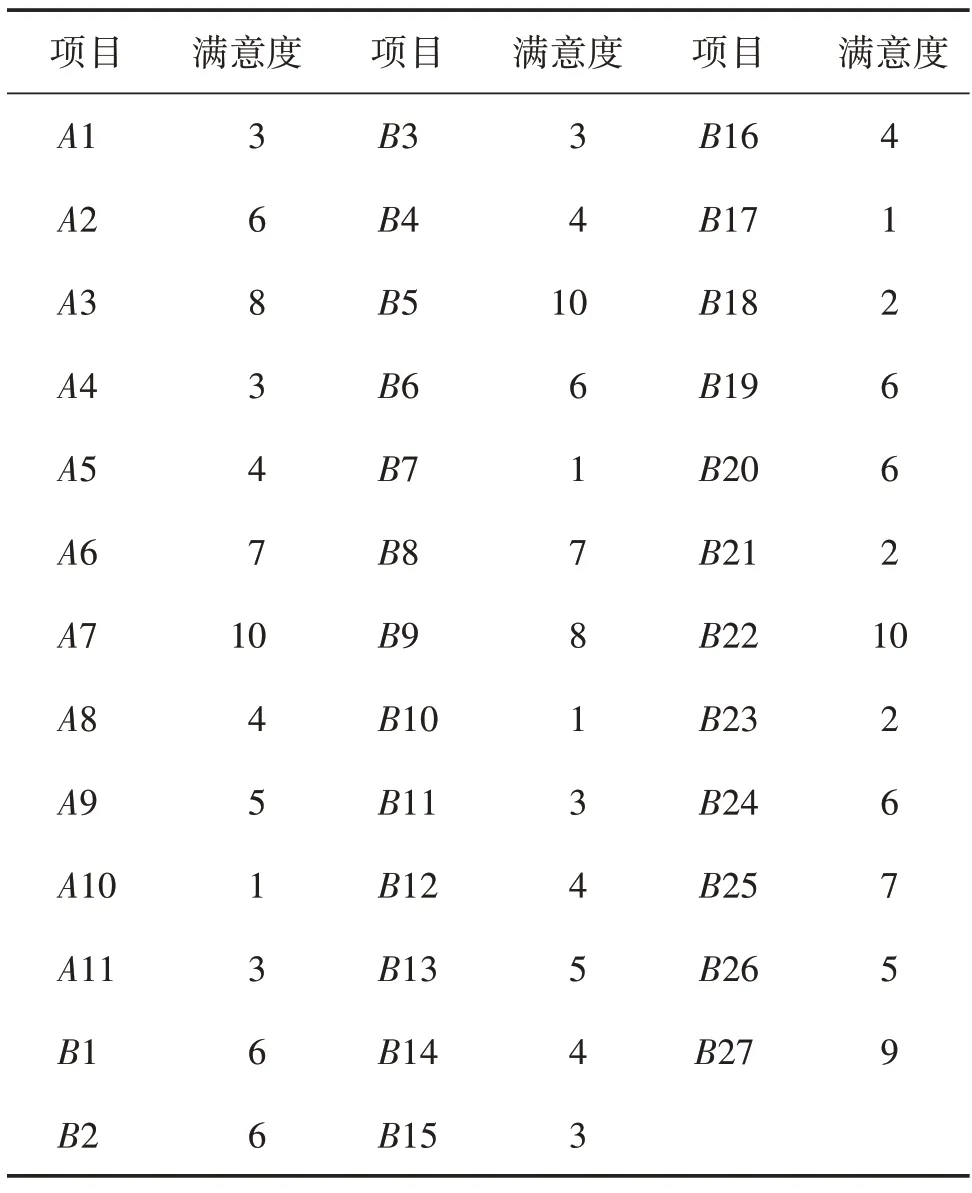
表5 各個項目的滿意度表

4 基于多元線性規劃的項目選擇模型

在前面的基礎上建立了相關多元線性規劃模型，其主要是以各個項目的滿意度為基礎，以時間為約束條件，以最大化滿意度為目標建立多元線性規劃模型，其中對是否選擇項目使用0-1 變量進行表達，為了方便使用matlab求解函數進行求解本文把優化目標加一個負號變成最小化的優化模型，得出其優化目標為：

采用單純形法進行求解。其具體求解步驟如圖3。

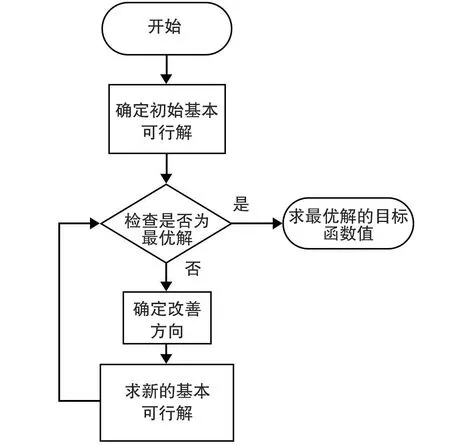
圖3 單純形法算法流程圖

先確定一個初始可行解，然后檢查基本解是不是最優的，如果最優則停止迭代，已找到最優值，如果不是進行下一步，移至目標函數值有所改善的另外一個基本可行解，重復之前步驟。

在確定了相關的項目內容后，具體確定其項目的順序，參考關聯度系數的計算方式來定義項目之間的二維距離關系然后構建遺傳算法求解類TSP 模型，其具體距離定義關系式：

最后用計算機編程獲得最后的結果，游玩順序如圖4。

圖4 項目游玩順序

通過遺傳算法進行優化求解，算法迭代很快，適應度曲線變化示意如圖5。

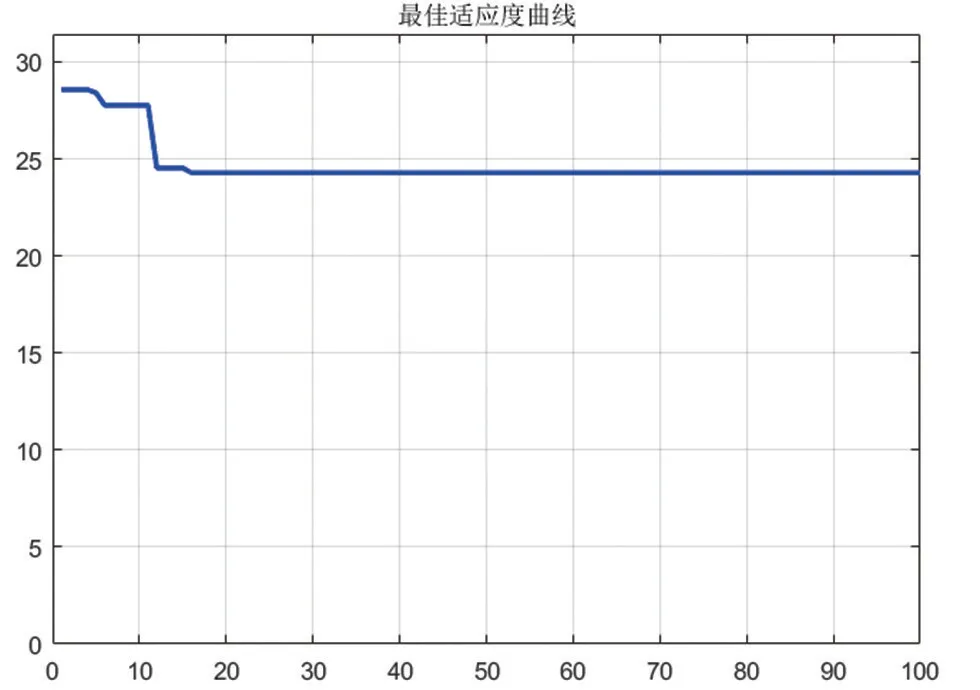
圖5 適應度曲線變化示意圖

5 結論

首先根據歷史數據，建立線性回歸模型，預測計算了2019 年8 月5 日A4，B5，B12，B25 四個項目當天的游玩人數，并通過排隊論，計算了每一個項目的平均排隊人數和平均等待時間。用層次分析法，構造了對比矩陣，得到了各個項目的滿意度表，最后用遺傳優化的類TSP方法得到了最佳游玩順序。