一種基于局域不可區分正交直積態的新型量子保密求和協議
王 躍, 張可佳,2, 藺苗苗
(1.黑龍江大學 數學科學學院, 哈爾濱 150080; 2.黑龍江大學 黑龍江省復雜系統與計算重點實驗室, 哈爾濱 150080)
0 引 言
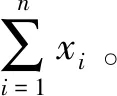
通過上述的分析,發現量子保密求和協議能通過不同的量子載體來實現,例如單光子[19]、Bell態[20]和d維糾纏態[21-22]等。最近,一種具有局域不可區分性的正交直積態引起了研究者們的廣泛關注。區別于單光子和糾纏態,這種新型量子態在局域操作和經典通信下不可區分,并且相比于糾纏態更容易制備。將這種量子態應用于量子密碼協議的設計中已成為研究者們關注的熱點,例如,基于正交直積態的量子密鑰分配協議[23]、基于正交直積態的量子秘密共享協議[24]、基于正交直積態的量子代理簽名協議[25]、基于正交直積態的量子支付協議[26]、基于正交直積態的多方量子簽名協議[27]和基于正交直積態的量子投票協議[28]等。進一步,本文考慮將這種具有局域不可區分性的正交直積態用于量子保密求和協議設計中。
本文介紹了在協議中所用到的一些基礎知識,包括量子保密求和協議所應該滿足的一些基本條件和協議的基本流程,分析了協議的正確性、隱私性和安全性,并對后續的研究內容進行了討論和總結。
1 預備知識
首先介紹協議中所使用的正交直積態。在3?3量子系統中,可以構造以下9個正交直積態:
|φ1〉=|1〉1|1〉2
|φ2,3〉=|0〉1|0±1〉2
|φ4,5〉=|0±1〉1|2〉2
(1)
|φ6,7〉=|2〉1|1±2〉2
|φ8,9〉=|1±2〉1|0〉2
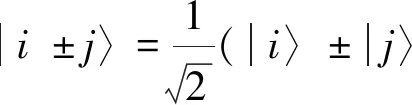
隨后,移位操作Ux定義如下:
(2)
式中:d為量子系統的維數,⊕為模d加,x=0,1,2,…,d-1。不難發現,對處于計算基下的量子態|t〉,t=0,1,2,…,d-1,執行Ux操作之后可得:
Ux|t〉=|t⊕x〉
(3)
(4)
2 基于局域不可區分正交直積態的量子保密求和協議
2.1 協議滿足的條件
在協議中,假設有3個參與者P1、P2和P3,每個參與者Pi手中有一個長為N的秘密串:
(5)
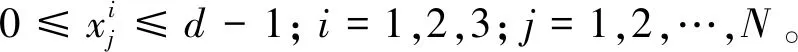
X=(x1,x2,…,xN)
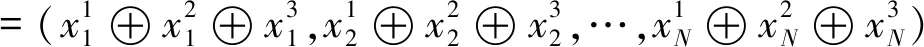
(6)
基于上述條件,量子保密求和協議應該滿足以下三個條件:
(1) 正確性: 每個參與者Pi輸入了自己的秘密數值Xi后,所有參與者經過一系列計算最終能夠得到正確的X。
(2) 隱私性: 每個參與者Pi除了得到求和的結果X之外,不能獲得其他參與者Xj(j≠i)的值。
(3) 安全性: 當外部的竊聽者想要獲得參與者Pi的秘密信息Xi時,就一定會被參與者P1檢測到。
2.2 協議的具體步驟
在3?3量子系統中,量子保密求和協議的具體步驟如下:
(1) 必要信息分發:首先,P1與P2和P3通過量子密鑰分配(QKD)技術共享相同的密鑰K=(k1,k2,…,kN), 其中kj=0,1,j=1,2,…,N。這里要求密鑰串K是均勻的,即其中0,1比特數相同。注意,當N的值為奇數時,在末位加kN+1=0。其次,P1制備N個量子態,每個量子態的形式隨機取自公式(1)的正交直積態,并且這N個量子態中包含公式(1)中的9個量子態。然后,P1將這N個量子態中的第一個粒子取出,形成序列S1=(|s11〉,|s12〉,…,|s1N〉);第二個粒子取出,形成序列S2=(|s21〉,|s22〉,…,|s2N〉)。同時,P1制備δ個隨機選自{|0〉,|1〉,|+〉,|-〉}的誘騙粒子,將這δ個粒子插入S1中得到S′1,再制備δ個誘騙粒子插入序列S2中形成S′2。最后,將序列S′1發送給P2,將序列S′2發送給P3。
(2) 秘密信息編碼:P2接收到S′1之后,P1公布誘騙粒子的位置和測量基。P2通過P1公布的測量基測量對應位置的粒子,然后P1和P2比對測量結果與P1初始制備的誘騙態是否相同。若錯誤率高于某個閾值,協議終止;否則,協議繼續,P2恢復序列S1。P2根據手中的密鑰K對粒子執行相應的操作生成新的序列T1:
(7)
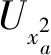
(8)
最后,P3在新的序列R1中隨機插入δ個誘騙粒子得到R′1并發回給P1。
類似地,P3在接收到S′2之后,對誘騙粒子進行檢測。檢測通過后,P3去除δ個誘騙粒子,序列由S′2變為S2,同樣根據密鑰K對粒子序列執行操作得到新的序列T2:
(9)
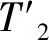
(10)
最后,P2在新的序列R2中隨機插入δ個誘騙粒子得到R′2并發回給P1。
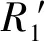
(11)
(4) 計算求和結果:P1首先使用相應的基測量余下的N個量子態,可以通過表1來獲得求和的結果:
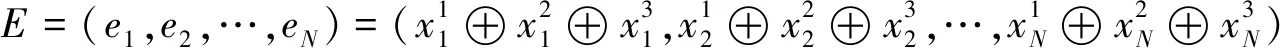
(12)
然后,P1公布計算結果。具體參與方之間交互的過程如圖1所示。
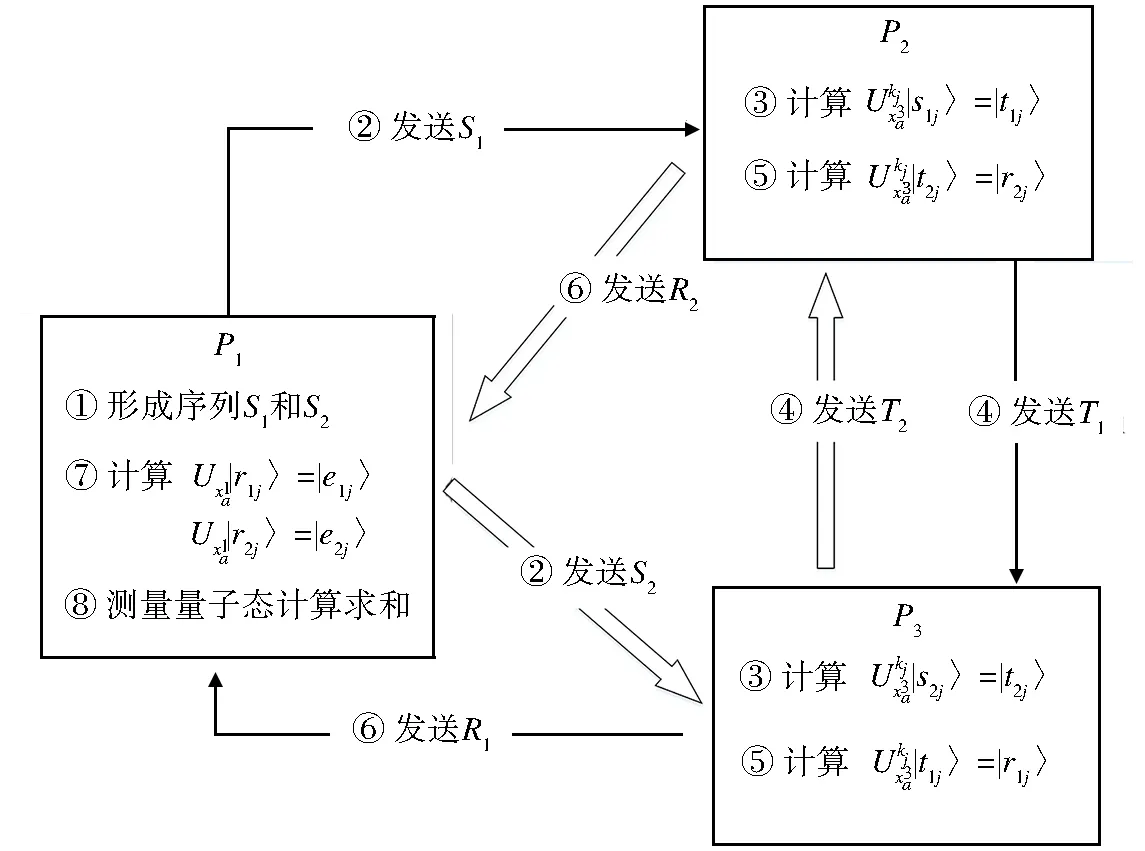
圖1 協議流程圖
3 協議分析與討論
3.1 正確性
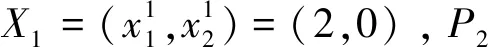
(13)
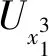
(14)
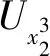
(15)
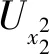
(16)
P3將粒子發送給P1。第三步檢測竊聽階段,P1收到粒子R1和R2后,將自己的秘密編碼到粒子上:
(17)
第四步計算求和結果,P1使用相應的基對兩個粒子分別進行測量,將測量結果對應表1得到求和結果E=(0,2)并公布。由此可知,協議可以得到正確的求和結果。
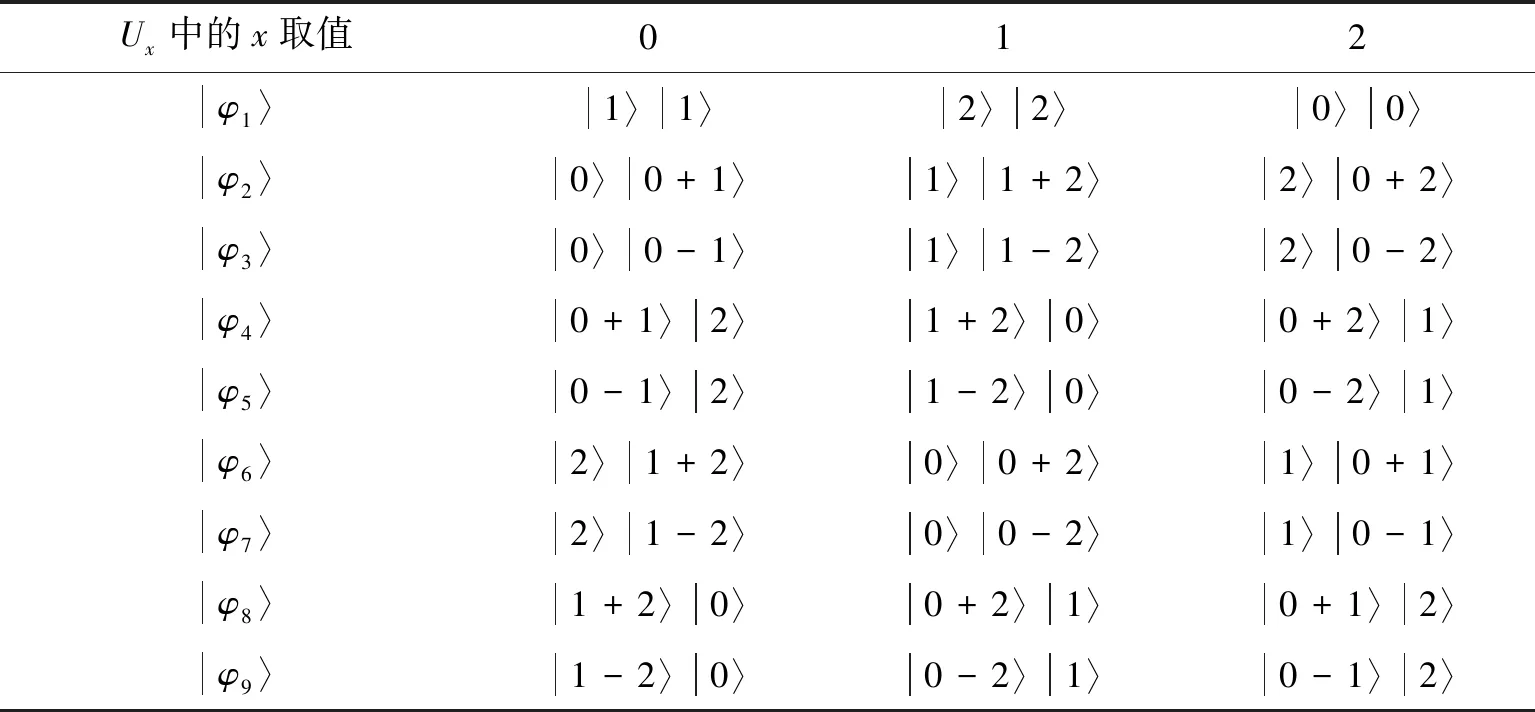
表1 執行移位操作之后相對應的結果
3.2 隱私性
隱私性即協議可以抵抗內部參與者Pi所發起的攻擊。由于Pi參與了協議執行的過程,所以他發起的攻擊往往比外部竊聽者Eve的攻擊更具危險。內部參與者攻擊可以分為兩種,第一種是單個不誠實參與者攻擊,第二種是兩個及兩個以上多個不誠實參與者的聯合攻擊。由于在實際中假設大多數參與者都是誠實的,因此在三個參與者的情況下,我們只需要考慮參與者的單獨攻擊即可。單個不誠實參與者的獨立攻擊又分為以下兩種情況:
(1) 參與者P2或P3發起的攻擊
由于參與者P2和P3攻擊手段相同,所以這里只分析P2所發起的如下攻擊:①P2竊取P1的秘密信息。由于P1的秘密信息是在粒子傳輸完回到自己手中后才編碼到粒子上的,所以P2無法獲得P1的秘密信息。②P2竊取P3的秘密信息。P2在第二步秘密信息編碼過程中,可能會實施截獲-測量-重發攻擊和糾纏-測量攻擊。
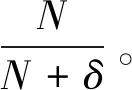
(18)
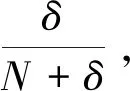
(19)
故而,P2得到正確的測量結果并且不被發現的概率為:
(20)
當N足夠大時,可能性趨近于零。P2測量完粒子后,根據測量結果,偽造粒子發送給P1。P1接收粒子后與P3一起檢測竊聽,當錯誤率高于某個閾值時,終止協議。
然后,以粒子{|0〉,|1〉,|0+1〉,|0-1〉}為例,來分析糾纏-測量攻擊。P2攔截了由P3發送給P1的粒子序列之后,制備輔助粒子|A〉,并對攔截的粒子和輔助粒子執行如下操作:
U|0〉|A〉=α|0〉|a00〉+β|1〉|a01〉
U|1〉|A〉=γ|0〉|a10〉+δ|1〉|a11〉
(21)
式中|α|2+|β|2=|γ|2+|δ|2=1,為了不改變截獲粒子的狀態,式(21)需要滿足:
β|a01〉=γ|a10〉=0
α|a00〉-β|a01〉+γ|a10〉-δ|a11〉=α|a00〉+β|a01〉-γ|a10〉-δ|a11〉=0
(22)
由式(21)和式(22)得:
U|0〉|A〉=α|0〉|a00〉
U|1〉|A〉=α|1〉|a00〉
(23)
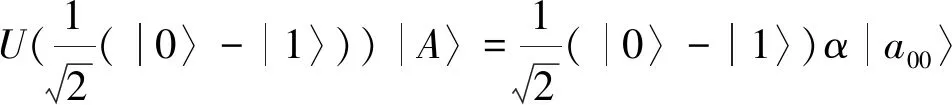
由此可見,P2不能通過對輔助粒子的測量獲得P1的秘密信息。綜上所述,參與者P2或P3發起的攻擊是無效的。
(2)量子態的制備者P1發起的攻擊
P1要想竊取P2和P3的輸入數值,會在第二步秘密信息編碼階段攔截由P2發送給P3的N+δ個量子態。P1是量子態的制備者,可以選擇相應的測量基對N個編碼秘密信息的粒子進行測量。由于不知道δ個誘騙粒子所處的位置和測量基,所以發送偽造粒子給P3之后,P3與P2將會以如下p的概率發現P1的竊聽行為:
(24)
當N足夠大時,p趨近于1。因此,本協議可以抵抗參與者P1發起的攻擊。
3.3 安全性
安全性即協議可以抵抗外部竊聽者Eve的攻擊。假設存在一個外部攻擊者Eve,在量子態的傳輸過程中想要實施一些竊聽行為。在第二步秘密信息編碼過程中,P1制備量子態之后,量子態以環形傳遞。Eve獲取由Pi發送給Pi+1的量子態,其中i=1,2,它對粒子可能實施截獲-測量-重發攻擊和糾纏-測量攻擊。然而,由于Eve不知道密鑰K的值,攻擊將改變處于kj=0位置的粒子,其中j=1,2,…,N,從而在檢測竊聽階段被P1發現,進而中止協議。
3.4 討論
僅利用3?3量子系統中的局域不可區分正交直積態來設計量子保密求和協議,這種思想也可以在d?d量子系統中實現。如在4?4量子系統中,可以通過與3?3量子系統同樣的方式構建一個量子保密求和協議。協議的具體步驟除第一步必要信息分發中P1所制備的N個量子態不同之外,其他步驟與上述的協議步驟相同。

表2 執行移位操作之后相對應的結果
P1在如下的4?4量子系統中的局域不可區分正交直積態中選擇N個量子態:
|φ1〉=|0〉|0〉 |φ10,11〉=|0±3〉|1〉
|φ2,3〉=|1〉|0±1〉 |φ12,13〉=|3〉|0±3〉
|φ4,5〉=|0±1〉|2〉 |φ14〉=|1〉|3〉
|φ6,7〉=|2〉|0±2〉 |φ15〉=|2〉|1〉
|φ8,9〉=|0±2〉|3〉 |φ16〉=|3〉|2〉
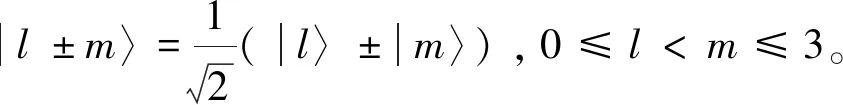
4 結 論
本文給出了將局域不可區分正交直積態應用于量子保密求和協議中的新方法,這之中還存在著一些沒有考慮到的一些情況,例如如何利用局域不可區分正交直積態在n個參與方中進行保密求和等等。相信隨著關于正交直積態研究的深入,這些問題都能夠得到有效的解決。本文基于局域不可區分正交直積態設計了一種新型的三方量子保密求和協議。理論分析表明,本協議可以確保正確性、隱私性和安全性。

