基于確定性擁擠的多模態郊狼優化算法*

陳丹妮，趙劍冬，高 靜

(1.廣東技術師范大學計算機科學學院，廣東 廣州 510665；2.廣東恒電信息科技股份有限公司，廣東 廣州 510630)

1 引言

多模態優化問題[1]是指優化的問題存在多個局部或者全局最優解，它普遍存在于我們的生活中，例如圖像分割、機械設計和電力系統規劃等。目前，群智能優化算法是解決多模態優化問題較為流行的一類方法。遺傳算法GA (Genetic Algorithm)[2]、模擬退火SA (Simulated Annealing)算法[3]、粒子群優化PSO (Partical Swarm Optimization) 算法[4]、蟻群優化ACO (Ant Colony Optimization) 算法[5]、螢火蟲算法FA (Firefly Algorithm)[6]、布谷鳥搜索CS (Cuckoo Search) 算法[7]、蝙蝠算法BA (Bat Algorithm)[8]、灰狼優化GWO (Grey Wolf Optimizer) 算法[9]、多元宇宙優化MVO (Multi-Verse Optimizer)算法[10]等群智能優化算法均是模擬自然界的現象規律或者生物種群的社會生活而提出的。Salcedo-Sanz[11]通過對大量群智能優化算法的研究，發現優化算法想要取得良好表現的基礎是在勘探和探索之間取得平衡。而上述算法在優化過程中較少關注勘探和探索兩者間的平衡，這可能限制了它們在多模態問題上的尋優能力。為了彌補上述不足，學者們提出了不少改進方法[12 - 16]，包括混合算法、環拓撲、局部信息和小生境技術等。

Pierezan等[17]受郊狼對生存環境的適應性及其社會結構的啟發，在2018年提出了郊狼優化算法COA (Coyote Optimization Algorithm)，該算法為在優化過程中平衡探索和勘探提供了新的機制。郊狼優化算法能有效地處理具有邊界約束的連續變量全局優化問題。然而，在現實世界中很多優化問題是多模態的，為了找到多模態問題的全局最優解，要求算法具有跳出局部最優的能力。在多模態情景下，郊狼優化算法的收斂精度和穩定性需要進一步提高。在此基礎上，受到小生境技術對其他群優化算法的應用效果啟發，本文提出了一種基于確定性擁擠的多模態郊狼優化算法DCCOA(Deterministic Crowding Coyote Optimization Algorithm)，旨在提高算法的收斂精度和穩定性。

本文的其余部分組織如下：第2節主要介紹郊狼優化算法和小生境技術的相關工作； 第3節詳細介紹本文提出的基于確定性擁擠的多模態郊狼優化算法；第4節對實驗結果進行理論分析；第5節給出結論和未來的研究工作。

2 相關工作

2.1 郊狼優化算法

COA算法將郊狼的生存環境狀況視為優化問題的變量，將郊狼對環境的適應能力作為優化目標。郊狼根據郊狼群組內的信息共享和不同郊狼群組間的信息交流更新自身對社會狀況的認知，各個郊狼群組經過多代郊狼的出生、交流、成長和死亡的更新迭代之后，整個郊狼群中環境適應能力最強的郊狼將被作為優化問題的最優解。COA算法與GWO算法不同的是：GWO算法關注狼群的社會等級和捕獵過程，而COA算法則將關注點聚焦在郊狼之間的交流和社會結構方面。

在國外，Güven?等[18]將COA算法應用于風力發電的經濟調度問題上，結果表明郊狼優化算法比遺傳算法和粒子群優化算法具有更低的燃料消耗和更好的性能。此外，Qais等[19]使用COA算法建立了高精度的三極管光伏模型。與此同時，Pierezan等[20]將文化算法的一些概念引入COA中，提出了文化郊狼優化算法，并將該算法應用于重型燃氣輪機的運行。上述研究都將COA算法應用于各種不同的實際問題。在國內，張新明等[21]提出嵌入全局引導和相互作用的郊狼優化算法，提升了COA算法的全局搜索能力，并應用于醫學圖像增強中的參數優化問題。此外，張新明等[22]還提出強化最優和最差狼的郊狼優化算法，通過引入全局最優郊狼引導操作，并且在最優郊狼的成長過程中嵌入一種隨機擾動，提升了算法的全局尋優能力。與現有的群智能優化算法相比，COA算法具有過程簡單、需要設定的參數較少等優點。但是，面對多模態優化問題時，COA算法的全局尋優能力不足，收斂精度和穩定性還有待提高。

2.2 小生境技術

1995年，Mahfoud[23]首次提出小生境技術，旨在促進遺傳算法形成并維持穩定的亞群體。目前，小生境技術[24 - 26]主要包括適應度共享、物種形成、擁擠和清除等方法。其中，適應度共享、物種形成和清除方法都需要設置小生境參數，而且這些參數的設置需要先驗知識。 擁擠方法是最早也是最簡單的小生境技術之一，包括原始擁擠OC (Original Crowding)方法[24]、確定性擁擠DC (Deterministic Crowding)方法[23]和概率擁擠PC (Probabilistic Crowding)方法[27]。 其中，確定性擁擠方法因為不需要任何小生境參數，而更受歡迎。確定性擁擠DC方法隨機選擇2個個體作為父代(P1和P2)，隨后生成2個新生子代(C1和C2)。在子代替換父代之前，DC方法綜合考慮子代與父代彼此之間的距離和適應度。因此，本文將確定性擁擠方法引入COA算法中。

Thomsen[28]在差分算法DE(Differential Evolution)中分別使用了適應度共享方法(SharingDE算法)和確定性擁擠方法(CrowdingDE算法),實驗結果表明，CrowdingDE算法具有更好的穩定性和收斂速度。為了解決多模態問題，Majumdar等[29]在入侵雜草優化算法中引入了擁擠技術，結果表明該算法比其他標準多模態優化算法具有更優的收斂精度。除上述文獻之外，還有許多群智能優化算法[30 - 33]使用DC方法來提高算法的收斂精度，跳出局部最優，保持多樣性等。郊狼優化算法也屬于群智能優化算法。為此，本文提出了一種基于確定性擁擠的多模態郊狼優化算法(DCCOA)，旨在提升算法在多模態問題中的全局尋優能力。

3 多模態郊狼優化算法

基于COA算法，DCCOA算法有3個核心的改進部分：(1)新的郊狼進化機制；(2)新的郊狼群組文化趨勢計算方法；(3)郊狼更新社會狀況認知的新方法。DCCOA算法的流程如圖1所示。

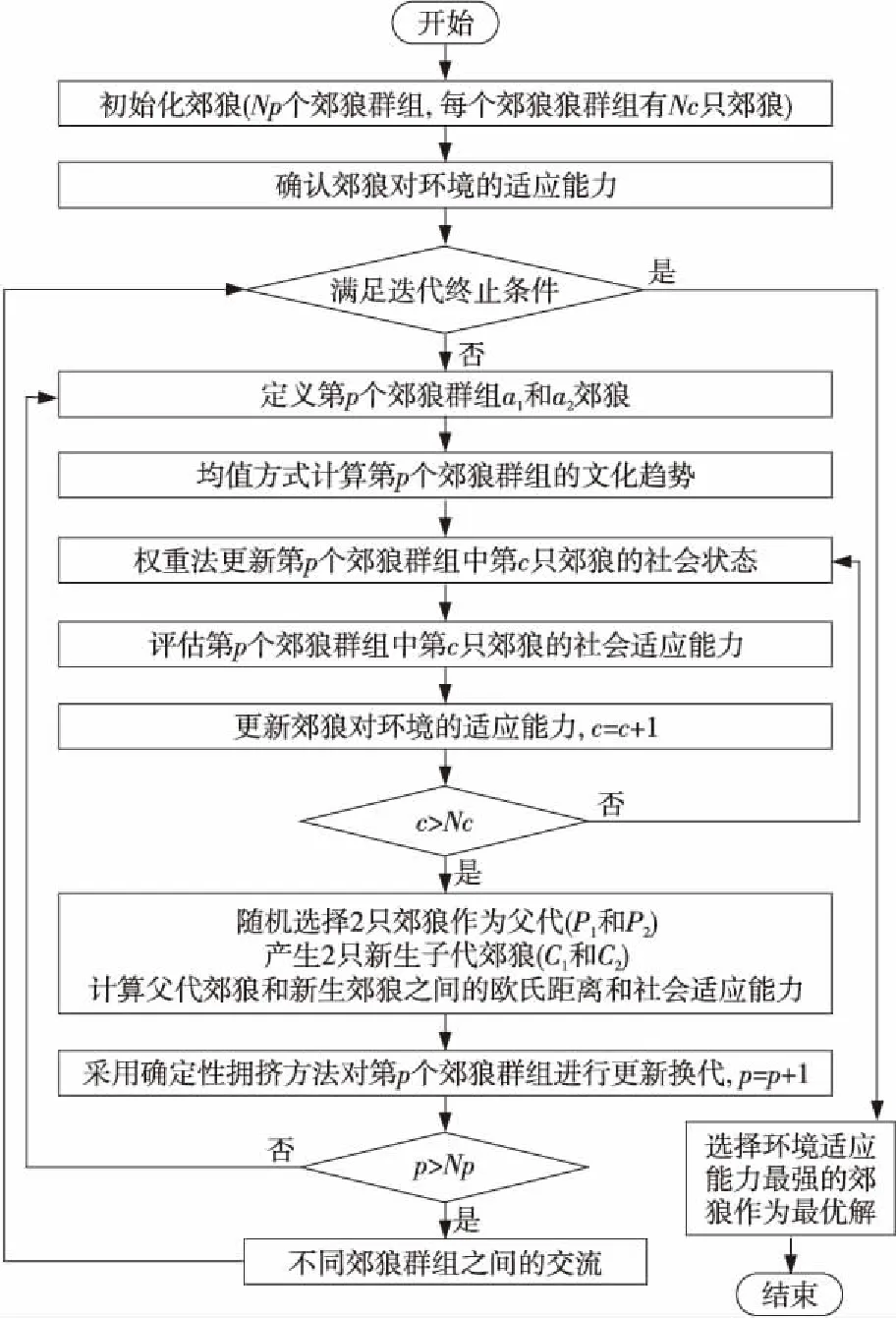
Figure 1 Overall of DCCOA

3.1 新的郊狼進化機制

在COA算法中，每代中每個郊狼群組只產生一只新生郊狼，而且這只新生郊狼能否存活取決于該郊狼群組中其他郊狼對環境的適應能力是否低于該新生郊狼。 然而，DCCOA算法采用確定性擁擠方法改進郊狼的進化機制。具體的步驟如下所示：

(1)從每個郊狼群組隨機選擇2只郊狼作為父代，記為P1和P2。

(2)在P1和P2郊狼和生活環境的影響下，產生2只新生郊狼作為子代，記為C1和C2。

(3)計算P1、P2、C1和C2郊狼對環境的適應能力，記為f(P1)、f(P2)、f(C1)和f(C2)。

(4)根據式(1)計算父代和子代郊狼之間的歐氏距離，記為EdP1C1、EdP1C2、EdP2C1和EdP2C2。

(5)根據父代郊狼和子代郊狼的適應能力和歐氏距離，采用確定性擁擠方法更新郊狼群組。

D維空間中，第b只郊狼的位置是Xb=(xb1，xb2，…,xbD)T，第d只郊狼的位置是Xd=(xd1，xd2，…,xdD)T，那么第b只郊狼和第d只郊狼之間的歐氏距離[34]為：

Edbd=‖Xb-Xd‖,b,d∈N

(1)

在新的郊狼進化機制內，只有在競爭的子代郊狼具有更好的環境適應能力情況下，它才能代替父代郊狼。 確定性擁擠方法是郊狼進化機制中的一個重要過程，它不僅保證了適應環境能力較強的新生郊狼得到存活，還確保了距離更接近的父代郊狼被存活的新生郊狼取代，以此來提升算法在多模態問題中的全局尋優能力。

3.2 新的郊狼群組文化趨勢計算方法

除了提出新的郊狼進化機制，DCCOA算法還改進了郊狼群組文化趨勢的計算方法。COA算法把每個郊狼群組中所有郊狼對環境適應能力的中位數作為該郊狼群組的文化趨勢。 雖然中位數有著不容易受到極端值影響的優點，但它并不能全面地反映總體情況。算術平均值是由總體數據計算得出的，它具有優良的數學性質，是實際應用中使用最廣泛的趨勢測量方法。本文考慮到在郊狼群體生活中，每只郊狼都會對其群組的文化趨勢有所影響，因此定義郊狼群的文化趨勢計算方法如式(2)所示：

(2)

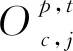
3.3 郊狼更新社會狀況認知的新方法

對于郊狼這個物種而言，每個郊狼群組中通常有2只阿爾法郊狼(α)，然而COA算法在每個郊狼群中只定義了1只阿爾法郊狼。為了更真實地模擬郊狼物種的社會生活，DCCOA算法在每個郊狼群組中定義了2只阿爾法郊狼(α1和α2)，它們是在每個郊狼群組中對環境適應能力最強的2只郊狼。考慮到最小化問題，在t時刻第p個郊狼群的α1和α2定義如式(3)和式(4)所示：

(3)

(4)

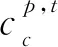
(5)

其中，ω1和ω2分別表示阿爾法郊狼α1和α2在其郊狼群組中對δ1的影響權重。經過多次調參實驗測試，ω1和ω2的值設為0.8和0.2時效果最優。

此外，COA算法在更新郊狼對社會狀況的認知時，設定阿爾法郊狼的影響(δ1)和郊狼群組文化趨勢的影響(δ2)是隨機的。然而，在郊狼種群的社會生活中，這兩者的影響權重并非隨機數。一般來說，阿爾法郊狼是每個郊狼群組中的強者，它們在郊狼更新對社會狀況的認知過程中有著較大的影響，而郊狼群組的文化趨勢影響則是潛移默化的，因此，在本文算法中，郊狼更新社會狀況認知的方式如式(6)所示：

(6)

其中，λ1和λ2分別表示δ1和δ2的影響權重。經過多次實驗測試，λ1和λ2的值設置為0.7和0.05時效果最佳。這也意味著在郊狼更新對社會狀況認知時，相比郊狼群組的文化趨勢影響，阿爾法狼有著更大的影響權重。

4 實驗對比

4.1 實驗設置與基準函數

為了評估本文提出的DCCOA算法的性能，將其與COA、PSO、GA、FA、CS、BA和MVO算法進行不同決策變量維數的多次實驗對比。其中根據文獻[17]將DCCOA和COA的參數Np和Nc分別設置為20和5，即郊狼總數為100。其他算法直接使用相應文獻設定的參數。實驗選擇了8個典型的基準函數，具體如表1所示。為了驗證算法在多模態問題中的全局尋優能力，8個基準函數包含2個單峰函數(F1和F2)和6個多峰函數(F3～F8),其中函數表達式中的n表示決策變量維數。

Table 1 List of benchmark functions used in the experiment

在上述基準函數上，8個算法分別在10維、50維和100維這3個不同決策變量維數上各獨立進行50次實驗。其中，當決策變量的維數為10維、50維和100維時，各算法的迭代次數分別為1 000次、2 000次和3 000次。實驗的硬件環境為：Intel(R) Core(TM) i5-4210U CPU @ 1.70 GHz,4 GB內存。軟件環境為：64位的Windows 10，Python 3.7.0。

實驗采用最小值、最大值、均值和方差這4個指標來衡量算法的性能。其中最小值和最大值分別代表在50次實驗中各算法能夠找到函數全局最優解的最好表現和最差表現；均值代表50次實驗中各算法的平均表現；方差代表各算法在實驗中的穩定性。

4.2 性能評估與理論分析

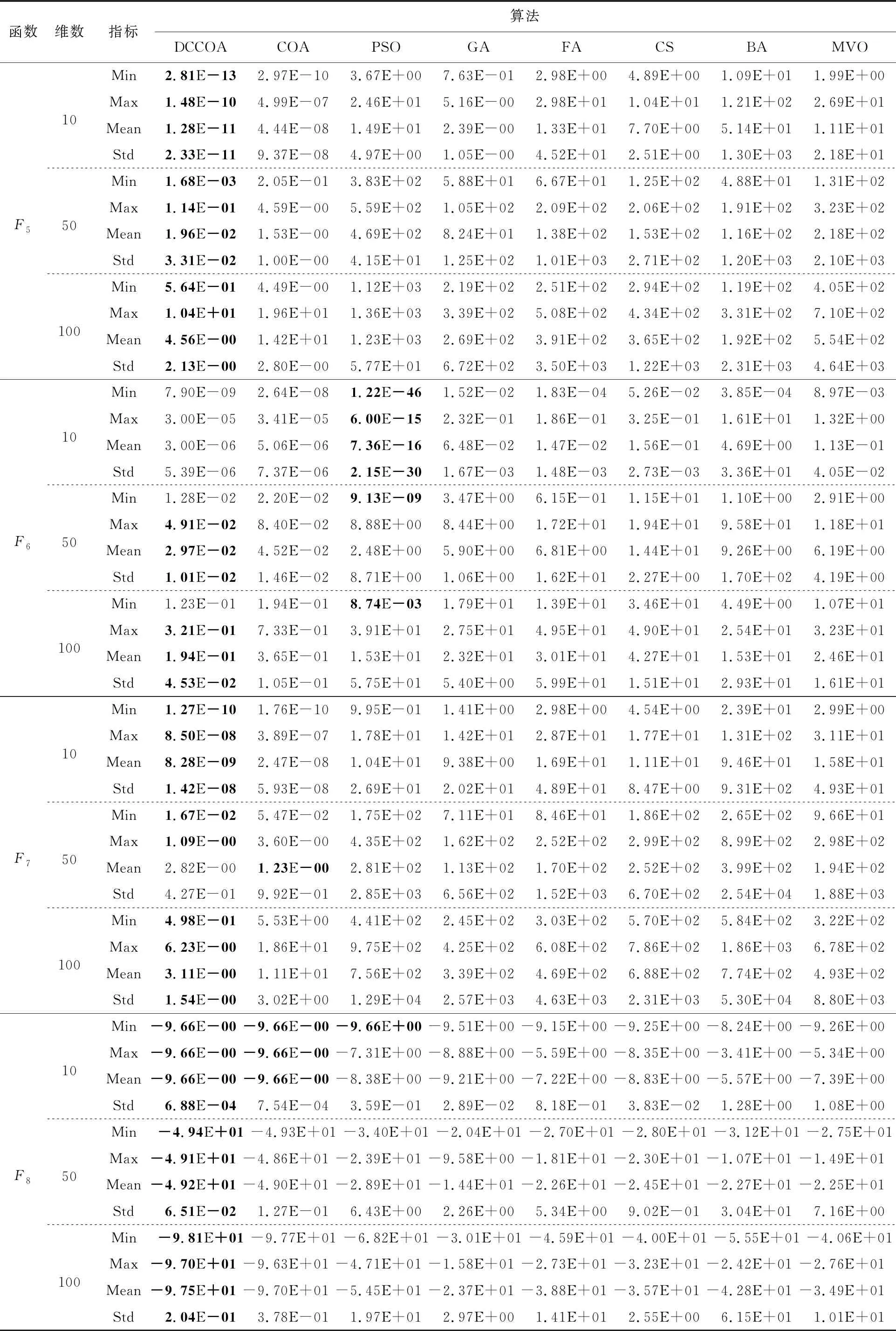
表2匯總了在不同決策變量維數下，8個算法在基準函數上的收斂精度和穩定性的統計結果，其中，對最佳結果進行加粗顯示。實驗結果表明，在3個不同的決策變量維數上，DCCOA算法在多個基準函數上的性能均優于COA算法的。DCCOA算法表現出更好的收斂精度和更強的穩定性，最優表現時將收斂精度和穩定性提高了4個數量級。

從收斂精度的角度來看，總體上，在多模態函數上DCCOA算法的表現更佳，在單模態函數上FA、CS和PSO算法的表現較優。對于F1函數，當決策變量維數為10時，DCCOA算法的收斂效果是最好的，這是因為在較低維數下，將平均值作為文化趨勢更有效地體現了每個郊狼群組中所有郊狼對社會狀況的認知對該郊狼群組的文化趨勢都有所貢獻。但是，隨著維數的上升，它的性能有所下降，此時，FA算法和CS算法的表現更勝一籌。這是由于布谷鳥搜索算法采用了隨機游走的萊維飛行操作和螢火蟲采用了相對亮度的引領操作，這讓它們在高維數的連續單模態曲面有更好的收斂精度。對于F2函數，PSO算法的表現較佳，這是因為粒子群體在尋優過程中會將歷史最優位置進行記憶并傳達給其他粒子，這讓其在單模態函數上具有較大的優勢。這一優勢也讓PSO算法在低維數的多模態F6函數上具有良好的表現。對于F3～F8函數，DCCOA算法展示出了很好的收斂效果，尤其在高度多模態F5和F7函數上以及搜索難度較大的F8函數上，它的收斂精度優于其他幾個算法。這是因為小生境技術的引入，進一步促進算法在尋優過程中平衡勘探和探索，從而提升算法跳出局部最優的能力。同時，更新郊狼對社會狀況認知的新方法更真實地模擬了郊狼的種群生活，也有利于更好地尋找全局最優解。

從穩定性的角度來看，CS算法在單模態F1函數上展示出了較強的穩定性。這是因為布谷鳥算法在光滑曲面上通過不斷隨機行走可以逐步接近全局最優解。在單模態F2函數上PSO算法具有較佳的穩定性。這是因為粒子在優化過程中充分利用自身信息和群體信息，在求解單模態問題時具有優異特性。對于多模態F3～F8函數，DCCOA算法表現出較強的穩定性，這是由于新的郊狼進化機制采用了確定性擁擠方法，它不僅保證了適應環境能力較強的新生郊狼的存活，而且還確保離新生郊狼較近的父代郊狼被替代，有利于維持郊狼的多樣性，提升算法在多模態問題上的穩定性。同時，新的更新郊狼對社會狀況認知的方法采用權重法和定義2只阿爾法郊狼，這都更符合郊狼的真實種群生活，對算法穩定性的提升有所貢獻。此外，FA算法在F4函數上也展現了較好的穩定性，這是由于在更新螢火蟲時同時考慮了確定性因素和隨機因素。

從收斂曲線的角度來看，整體上，BA算法和PSO算法最容易陷入問題的局部最優解，與此同時，BA有著更快的收斂速度；DCCOA算法和COA算法的表現相對穩定。在單模態函數上，8個算法在較低決策變量維數的表現沒有太大的差異，但是隨著維數的上升，PSO算法的性能有明顯下降。在多模態函數上，PSO算法跳出局部最優的能力較差，這是因為它在尋優過程的勘探和探索之間沒有取得平衡。BA算法雖然展示出了較快的收斂速度，但是它同樣容易陷入問題的局部最優解。相比COA算法，DCCOA算法在大多數情況下展示出稍快的收斂趨勢和較優的收斂精度。這是因為新的郊狼進化機制采用了確定性擁擠方法，它有利于進一步促進算法在勘探和探索之間的平衡，從而提升算法在多模態問題中的全局尋優性能。

5 結束語

為了解決多模態優化問題，本文提出了一種基于確定性擁擠的多模態郊狼優化算法(DCCOA)。該算法對COA算法做了3方面的改進，具體包括新的郊狼進化機制、新的郊狼群組文化趨勢計算方法和郊狼更新對社會狀況認知的新方法。為了評價DCCOA的性能，將其與COA、PSO、GA、FA、CS、BA和MVO算法在多個基準函數上進行實驗。實驗結果表明，相比COA算法，本文算法展示出更高的收斂精度、更快的收斂速度和更強的穩定性。本文證明了將確定性擁擠方法應用到郊狼優化算法上可進一步提升算法在勘探和探索之間的平衡能力，從而提升算法在多模態情況下的全局尋優能力。這是因為在更新郊狼群時，距離相近并且對環境適應能力較差的郊狼被淘汰。然而，本文還存在許多局限性，其中之一就是算法的計算時間相對較長。因此，在之后的工作中，將打算用平行策略進行搜索，以縮短算法尋優時間。

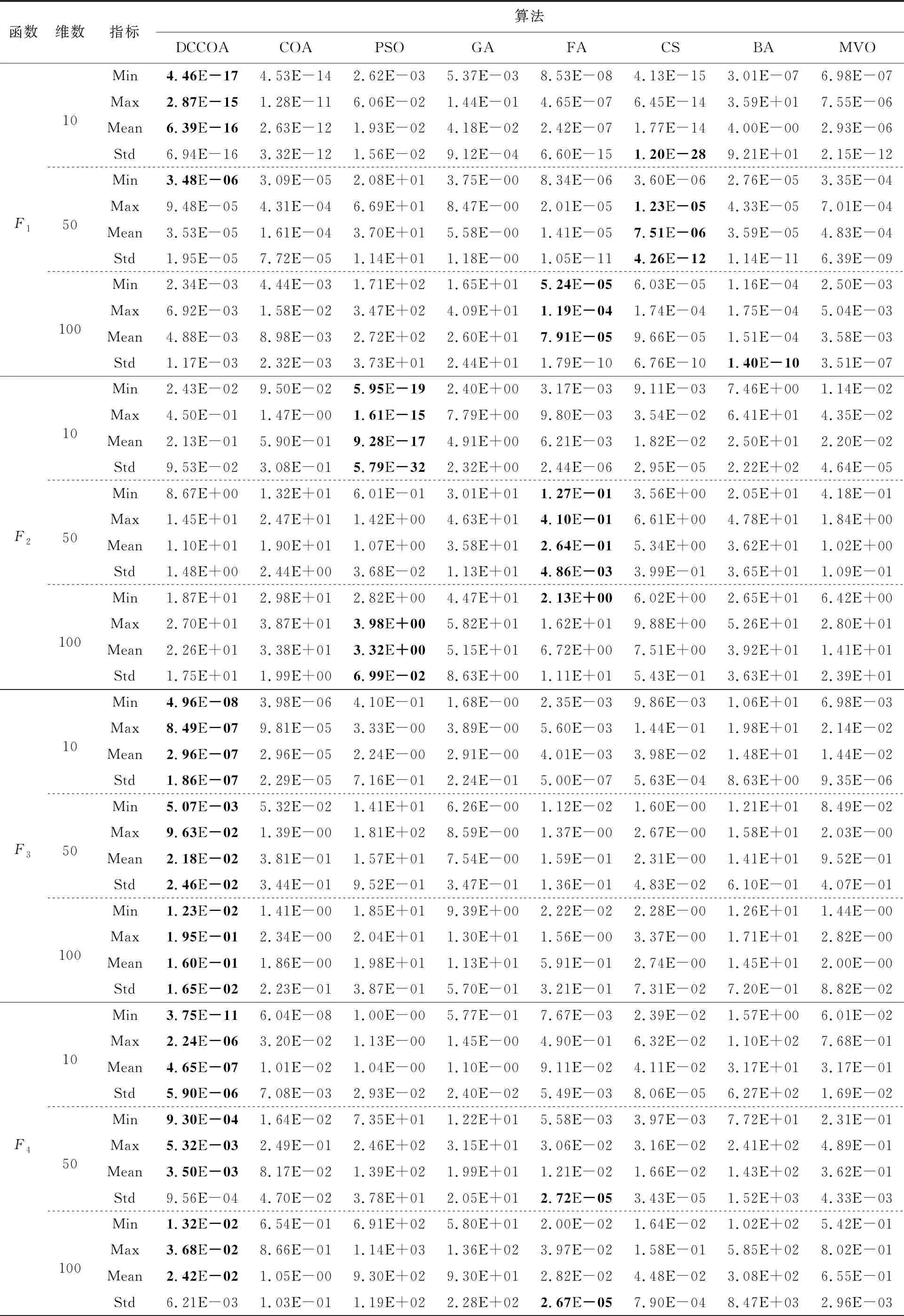
Table 2 Experimental results of eight algorithms on benchmark functions

續表