基于一種新型分支定價算法的電動車支線鎮際快遞配送路徑規劃研究*

師欣欣，陳樹國，馬 弘，鄧明榮

(1.浙江大學管理學院，浙江 杭州 310058；2．國網浙江省電力有限公司，浙江 杭州 310007;3.浙江大學工程師學院，浙江 杭州 310015)

1 引言

伴隨著互聯網經濟的蓬勃發展，網上購物成為人們消費活動的重要組成部分，國內對快遞的配送需求也呈現爆發式增長態勢。2019年，中國快遞服務企業業務量累計完成630億余件，其中農村快遞增速比城市高近10個百分點[1]。支線鎮際的快遞配送是影響配送整體效率和服務水平的重要環節，快遞的大規模和高時效性特點為支線鎮際配送問題提出新的要求和挑戰。與此同時，隨著新能源汽車在續航、充電時間等方面的表現日益提升，將電動汽車引入支線鎮際快遞配送成為可能，并將有助于物流行業綠色經濟的發展。本文主要對電動汽車在城鎮快遞配送中的路徑規劃進行研究，并提出與之相適應的分支定價算法求解該問題。

本文以支線鎮際快遞配送系統為研究對象，給定運營周期內城鎮之間的快遞配送需求，要求結合電動車輛自身屬性，決策車輛的行駛路徑和充電地點及時長，在滿足所有運輸需求的前提下，最小化總運輸成本。由于Kerivin等[2]證明了SPDPR問題(the Splittable Pickup and Delivery Problem with Reloads)的復雜度為NP-hard，本文的研究問題較SPDPR問題附加考慮了多種車型以及電動車輛的相關特性，使得SPDPR問題成為了本文研究問題的一個特例，因而本文研究問題的復雜度亦為NP-hard。

已有的與城際、鎮際快遞配送應用相關的研究，大多圍繞啟發式算法和智能優化算法展開。Smilowitz等[3]在運輸模型中將航空配送系統的剩余運力納入考慮之中，利用割平面法計算問題下界，并提出一個高效的線性規劃取整算法獲得問題可行解。Li等[4]則在有資源管理約束的服務網絡設計中考慮到異車型的問題。該研究將原問題分解為2個子問題，并利用禁忌搜索不斷指導和調整2個子問題的求解。在精確求解算法方面，Andersen等[5]針對鐵路運輸系統設計與之對應的分支定價算法，對小規模和中等規模問題實現了高效求解。但是，由于研究對象為鐵路運輸系統，模型并未涉及多車型、倉儲管理、充電樁管理等本文研究所必須要考慮的問題。

分支定價作為精確求解整數規劃問題中的經典算法，已經被廣泛應用于車輛路徑規劃、網絡設計和背包問題等各個研究領域中[6 - 8]。在本文的研究問題中，分支定價算法的應用要求對電動車輛建立基于路徑的數學模型，和經典的基于邊構建的模型相比，該模型提供了更優的問題下界，同時規避了車輛之間建模對稱性所帶來的困擾，有利于問題的高效求解。針對不同的應用場景，分支定價算法框架中的分支策略、子問題求解策略、割平面策略和強化策略等部分都需要完成有針對性的算法設計。基于上述研究，本文針對電動汽車在鎮際快遞配送的路徑規劃這一問題提出相應的分支定價算法，給出有利于平衡搜索樹的分支策略，結合割平面策略，用Java語言進行了實現。在實驗部分，將分支定價算法與求解器和經典的啟發式算法進行比較，實驗結果驗證了本文算法的可行性和有效性。

2 問題描述與模型建立

在鎮際快遞配送系統中，某2個城鎮中轉站之間每隔一段時間會產生一批新的快遞運輸需求，即需要將一定數量快遞包裹在規定的時間窗內從城鎮中轉站1送達城鎮中轉站2。在運輸車輛資源有限的情況下，為進一步節約運輸成本，降低車輛空駛率，本文規定該配送系統支持以下2種運輸規則：

(1)同一批貨物可以以任意數量被分裝在不同的車輛上進行運輸。

(2)每個城鎮中轉站配有倉庫，可以臨時存放貨物，貨物在中轉站可以選擇更換運輸車輛。

在時間維度，與文獻[5]相同，本文假設快遞運輸需求和車輛路徑都具有周期性重復的特點。所有快遞運輸需求的時間窗長度不超過一個運營周期，每輛運輸車的配送路徑要求在一個運營周期形成環路。通過圖1中的運輸方案來說明該假設。在該實例中，運營周期為10 h。表1列舉了5批待完成運輸需求的信息，其中需求D1的貨物數量為30，需要從城鎮中轉站2運往城鎮中轉站3，在某個配送周期內，最早取貨時刻為1，要在當前配送周期的時刻5之前送達。注意到需求D3、D4和D5的最晚送達時刻小于或等于最早取貨時刻，此時最晚送達時刻所在周期指相對于最早取貨時刻所在周期的下一個運營周期，即允許需求的時間窗跨越周期。在圖1中，2輛電動汽車完成了D1到D5的運輸需求。載重量為50的車輛1在1時刻從城鎮2出發，途徑城鎮3、城鎮4，到達城鎮中轉站4后在其充電樁充電1 h并空閑等待3 h后從城鎮4出發返回城鎮2。載重量為20的車輛2在1時刻從城鎮5出發，途徑城鎮3、城鎮1、城鎮2、城鎮1,在一個周期后返回城鎮5。需求D3被拆分成2批(數量為10和20)進行運輸，數量為10的貨物首先由車輛2運送至城鎮中轉站2的倉庫存放4 h后由車輛1運往目的地城鎮3。

為了更好地描述問題，與文獻[9]類似，本文選擇在時空網絡(Time-Space Network)上構建模型。在時空網絡中，原配送網絡中的每一個城鎮中轉站以及每一條邊在每一個時刻均有一個備份，使得時空網絡中的每個點和邊既定位空間也定位時間。如圖2所示，網絡中共包含2類邊，運輸邊和等候邊。運輸邊代表快遞包裹或電動汽車實際的空間位置轉移，等候邊代表快遞包裹在倉庫存放等候或者電動汽車在某中轉站充電或者等候。注意到由于問題具有周期性，在周期末尾的邊會循環指向周期開始，代表進入下一個新的運營周期。

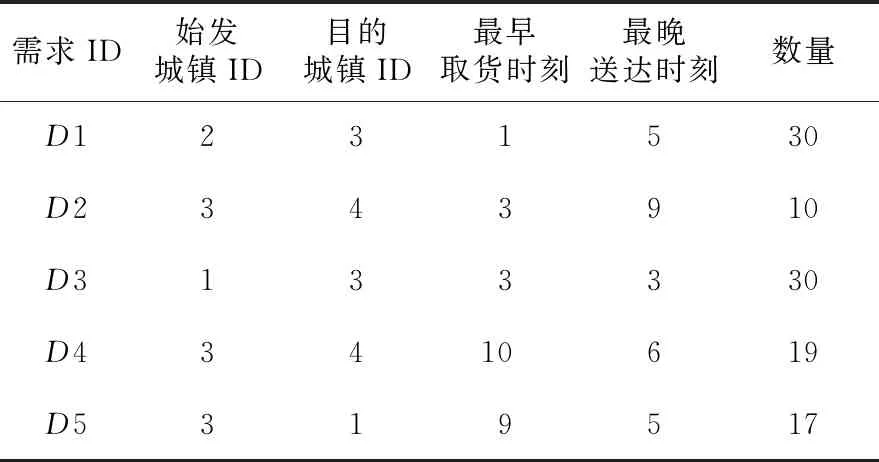
Table 1 Delivery demand example

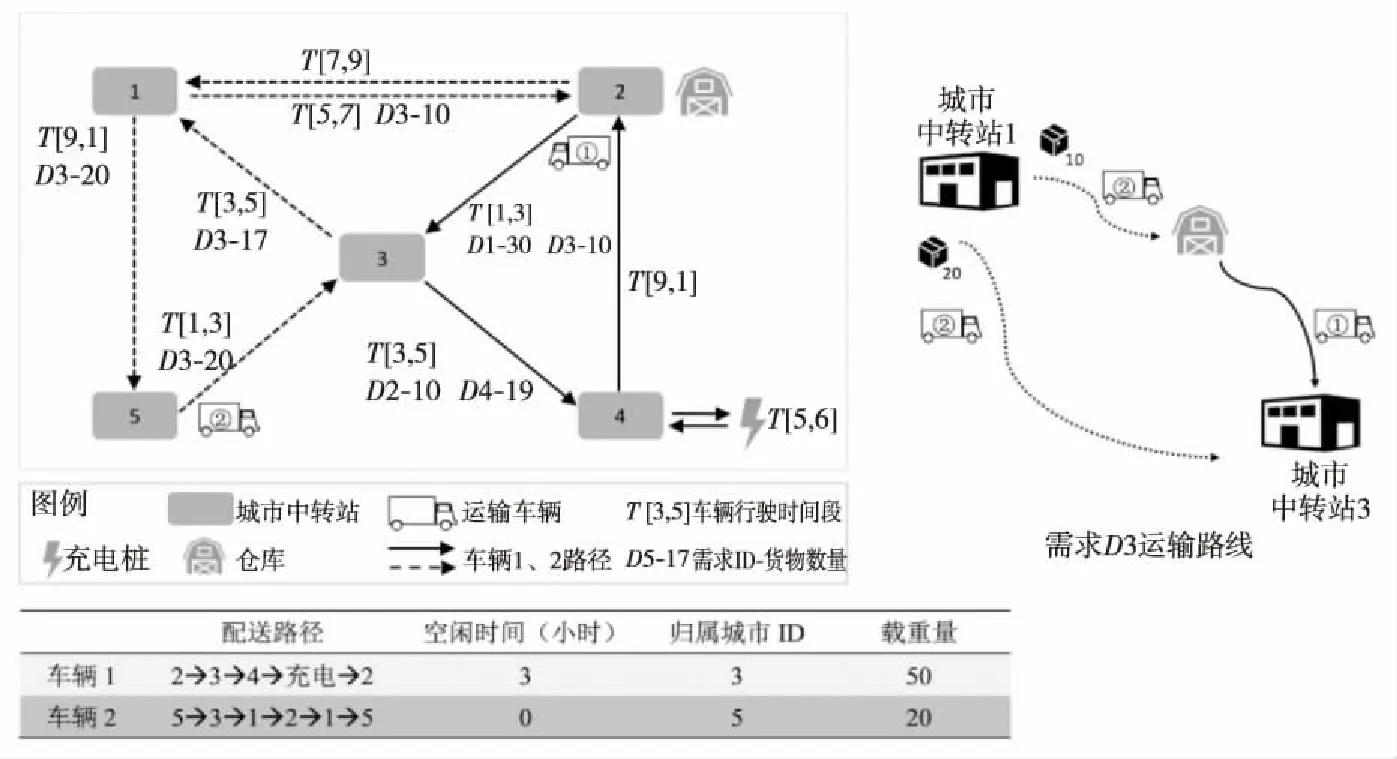
Figure 1 An example of transportation solution

Figure 2 Time-space network

2.1 符號說明

記G(N,A)代表時空網絡。假設每一個城鎮中轉站配有固定數量的充電樁。N代表時空網絡中點的集合，A代表時空網絡中的邊集，包括運輸邊集E和等候邊集H，記為A=E∪H。將整個時間周期劃分為離散的時刻T={1,2,…,Tmax}，對于實際的物理中轉站集合L，有N=L×T={lt|l∈L,t∈T}，其中lt代表t時刻的中轉站l。定義s(o,d)∈S為一個運輸服務，它包含了時空網絡中從中轉站o到中轉站d的所有時刻的運輸邊的集合。

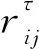
2.2 模型構建

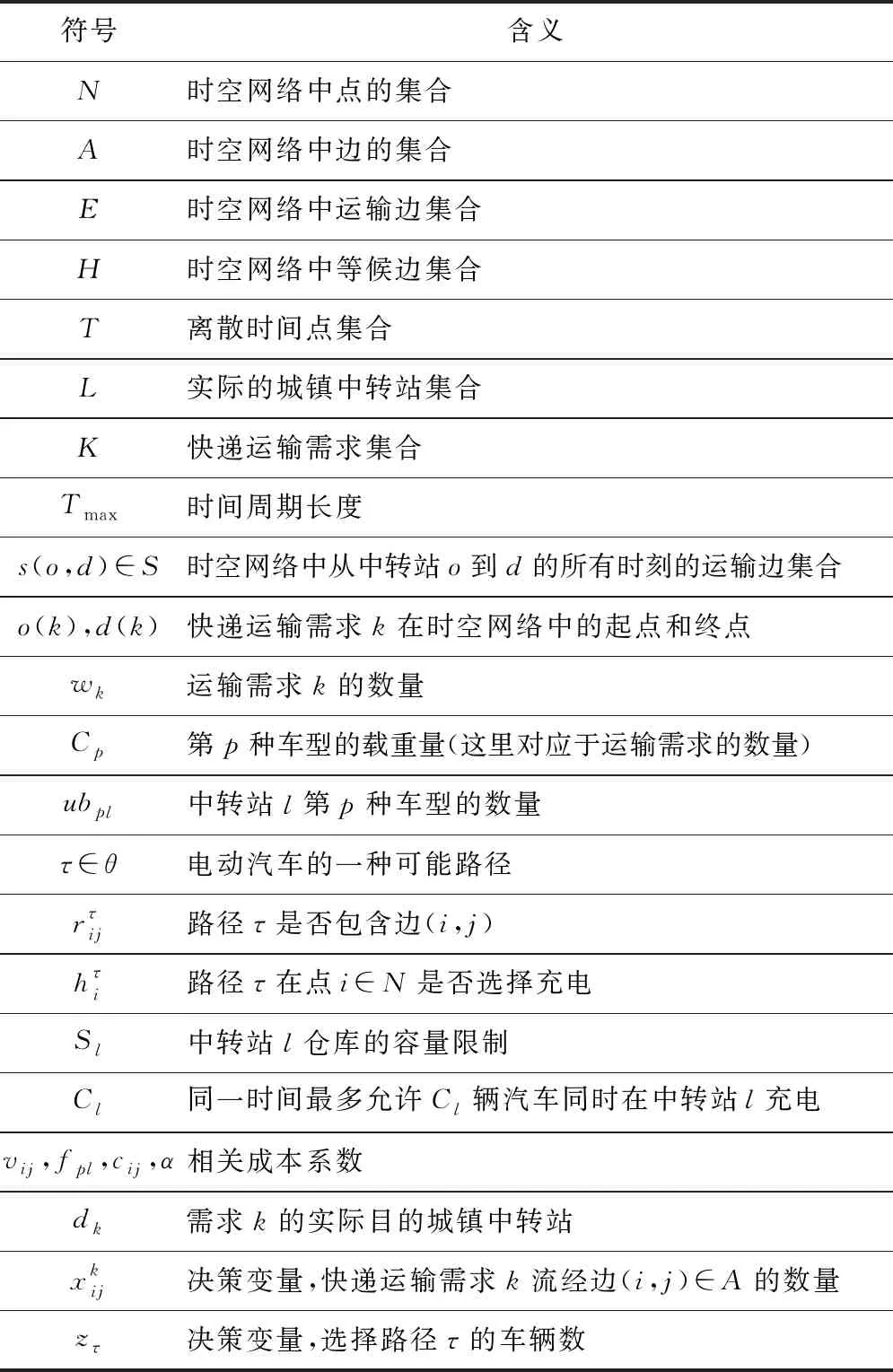
Table 2 Notation list

(1)

(2)

(3)

(4)

(5)

(6)

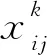
(7)

zτ∈N,?τ∈θ

(8)

約束(2)保證所有運輸需求都在規定的時間窗內被滿足。約束(3)限制在所有的運輸邊上，貨物總量不得超過車輛的總載重量。約束(4)代表每個中轉站l最多派出車型為p的汽車數量為ubpl。約束(5)保證了每個中轉站的倉庫在各時刻容納的快遞貨物量不超出其容量限制。所以，對于時空網絡中的每一個點lt∈N，將從該點出發的等候邊上的所有非終點貨物流相加，計為存放在當前倉庫的總貨物量。dk為需求k的實際目的城鎮。這里，為了簡化模型中可能涉及的倉庫存儲成本，本文假設當快遞被送達目的城鎮的中轉站時，它即刻從該中轉站分撥至快遞貨物目的地具體地址附近，而不再占用中轉站的倉儲資源。約束(6)限制每個中轉站同時充電的最大車輛數。

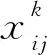
3 分支定價算法設計

為了獲得更高質量的LP松弛值，并且消除基于車輛構建模型中車輛同質所引起的對稱性問題[10]，本文選擇基于路徑構建模型。這相當于對經典的基于邊構建的模型進行Dantizg-Wolfe分解[11]，模型中會包含大量車輛路徑決策變量。對于該模型，列生成算法有助于求解其LP松弛問題(zτ松弛為實數變量)。算法主要在受限主問題RMP(Restricted Master Problem)和子問題之間協調計算。為了檢查RMP中的解對于主問題MP(Master Problem)是否已經最優，子問題將被求解。在本文算法中，每一個中轉站l和每一種車型p均對應于其中一個子問題。將列生成算法應用在分支定界搜索樹中的每個節點，即為分支定價算法，算法流程如圖3所示。

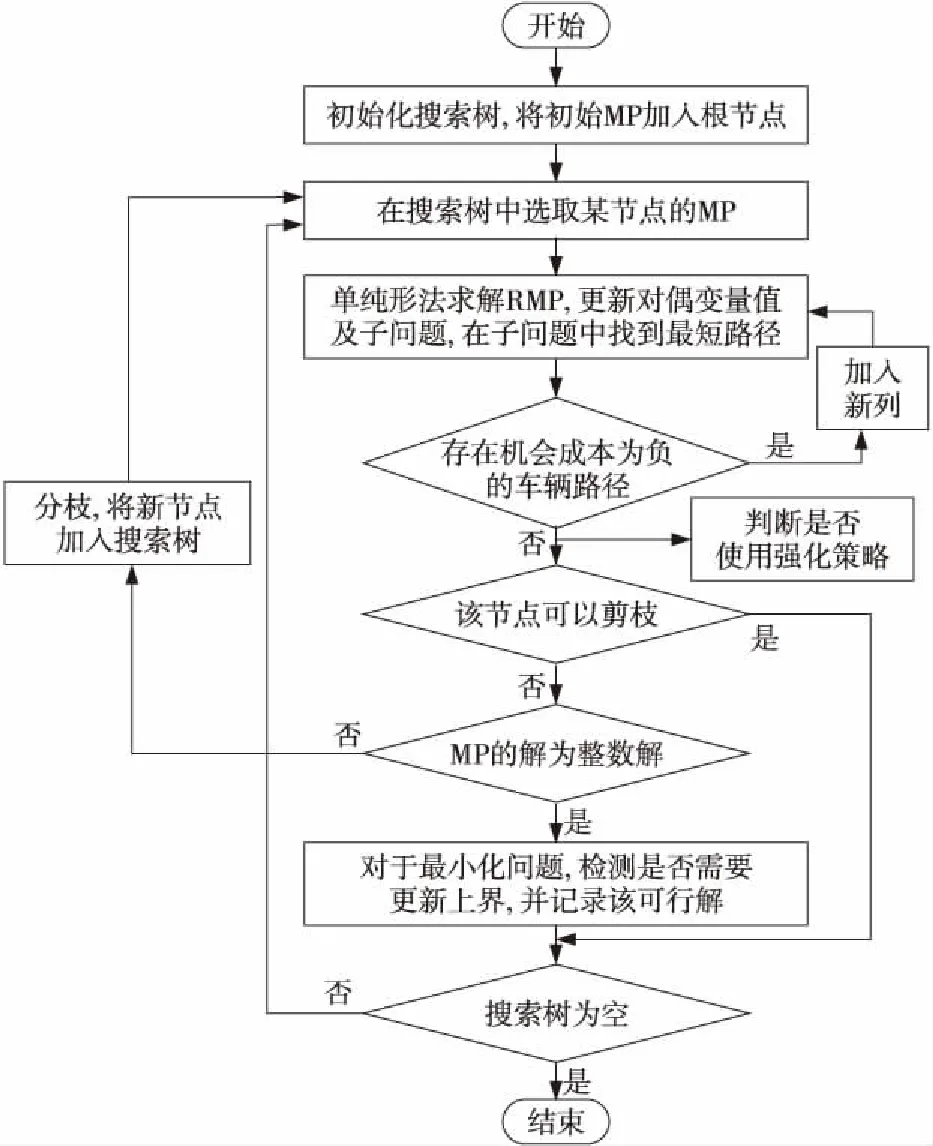
Figure 3 Flow chart of the branch and price algorithm

3.1 受限主問題RMP

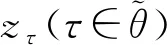
3.2 分支策略

在分支定價算法中，本文采用了3種分支策略，分別是服務分支策略、子問題服務分支策略和運輸邊分支策略。3種分支策略的執行優先權依次遞減。當得到某LP實數解時，首先考慮是否可以執行服務分支策略，如果不滿足條件，則繼續檢查是否可以執行子問題服務分支策略，最后檢查運輸邊分支策略。運輸邊分支策略可以保證最終得到可行解。

3.2.1 服務分支策略

服務分支策略針對所有子問題的某一服務s(o,d)∈S來進行分支，即所有電動車輛提供服務s(o,d)的數量之和需要為整數。服務s(o,d)為包含了時空網絡中所有時刻從中轉站o到d的運輸邊集合。本文通過向RMP中加入以下相對應的約束來進行分支操作。

(9)

(10)

3.2.2 子問題服務分支策略

同服務分支策略類似，子問題服務分支策略針對某一子問題的某一服務s(o,d)∈S來進行分支，即從某中轉站l∈L出發，第p∈P種電動車輛提供服務s(o,d)的數量之和需要為整數。RMP中對應的分支約束如下所示：

(11)

(12)

3.2.3 運輸邊分支策略

在運輸邊分支策略中，檢查每個子問題中電動車輛走過某一運輸邊的數量和是否為整數，若存在非整數，同樣選取小數部分最接近預先設點值的一條運輸邊a∈E進行分支。該分支對應于RMP中的約束(13)和(14)。運輸邊分支策略可以保證最終的解為可行解，但它往往會造成搜索樹2個分支的不平衡，本文將它放在分支策略中的最后來保證解的可行性。

(13)

(14)

3.3 割平面策略

在該問題中，本文還使用了普遍應用于服務網絡設計問題的強限制約束(Strong Forcing Constraint)。由于該強制約束數量眾多，本文將其作為割平面策略，只在適當的時候采用并將其加入到RMP中。由式(15)可看出，每一條運輸邊和每一批運輸需求均對應于一個強限制約束。

(15)

3.4 子問題

物流配送中電動汽車在很多方面具有與傳統汽車不同的特征[12]。本文假設電動汽車通過在中轉站的充電樁充電來進行能量供給，且采用部分充電模式，充電的最小時間單位同時空網絡。假設充電時間和充電可供行駛里程成線性關系，單位時間充電可供電動汽車行駛里程為g。為方便起見，將電動汽車的電池容量同樣用行駛里程來衡量，假設所有車輛的電池容量為Power。

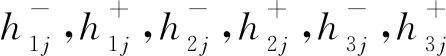
(16)

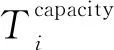
(17)

(18)

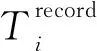
(19)

(2)當考慮在點i充電時，對于以點i為首的等候邊(i,j)∈H，生成下列新標簽：

(20)

(21)

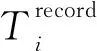
(22)

其中，chargeMark表示該路徑處有充電行為。

在本文的列生成算法中，針對特定子問題中的每個出發時刻，求出其最短路徑，若機會成本為負則將該最短路徑變量加入RMP中進行下一輪求解。

3.5 強化策略

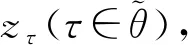
在本文提出的分支定價算法中，每隔一定數目節點的LP問題被求解后，會使用一次強化策略。首先統計出2個變量，cycleSet和lpColumnCount,其中，cycleSet代表當前列生成算法產生過的所有路徑變量構成的集合，lpColumnCount代表上述路徑變量對在所有節點LP最優解中的值的和。接下來以lpColumnCount為依據對cycleSet中的路徑變量進行篩選，識別cycleSet中的關鍵路徑變量并將其加入求解器，有利于強化策略在短時間獲得更高質量的可行解。

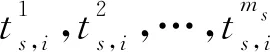
(23)

至此，計算出所有組組內路徑變量之間的距離并將其存儲在cyclePairList中。在圖4所示算法(其中包含了本文提出的路徑變量篩選算法)中，我們設置targetSize為將路徑變量集合篩選后的目標集合大小。路徑變量篩選算法根據lpCoumnCount提供的信息篩選出對問題求解關鍵的路徑變量集合并輸出該集合。

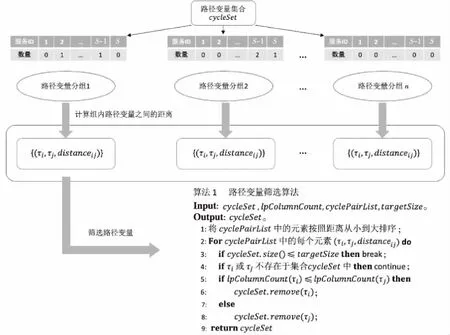
Figure 4 Flow chart of the intensification strategy

4 數值實驗與分析

本節中的數值實驗在安裝了CentOS Linux 7，配置了Intel Pentium 3.5 GHz處理器與16 GB內存的PC機上完成。使用Java 1.8實現了分支定價算法，并使用IBM ILOG CPLEX 12.6.1求解LP與MIP問題。源代碼已上傳至github網站(https://github.com/JAIMX/ESNDRC/tree/dev/paper)。在實驗部分，首先針對小規模算例將分支定價算法同直接用求解器求解做對比，以探究分支定價算法在精確求解小規模算例方面的性能。其次針對中等規模用例，使用分支定價算法和基于列生成的啟發式算法來求解并進行比較，以探究分支定價算法對中等規模問題的求解效果。

4.1 算例說明

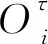
從文獻[5]的實驗數據中挑選了數據集1～12，其中5組小規模數據集構成測試算例1～5，其允許在有限時間內枚舉出所有可能的路徑τ并將其對應變量加入求解器中求解。7組中等規模數據集中，每組又加入了2個隨機生成的數據集以構成測試算例6～12。

將各算例的規模總結如表3所示。數據生成時，對于每一個中轉站，保證車輛固定使用成本隨著車輛容量增大而增加。根據每組算例的具體規模，在保證有可行解的前提下，相關參數的區間取值如表4所示。

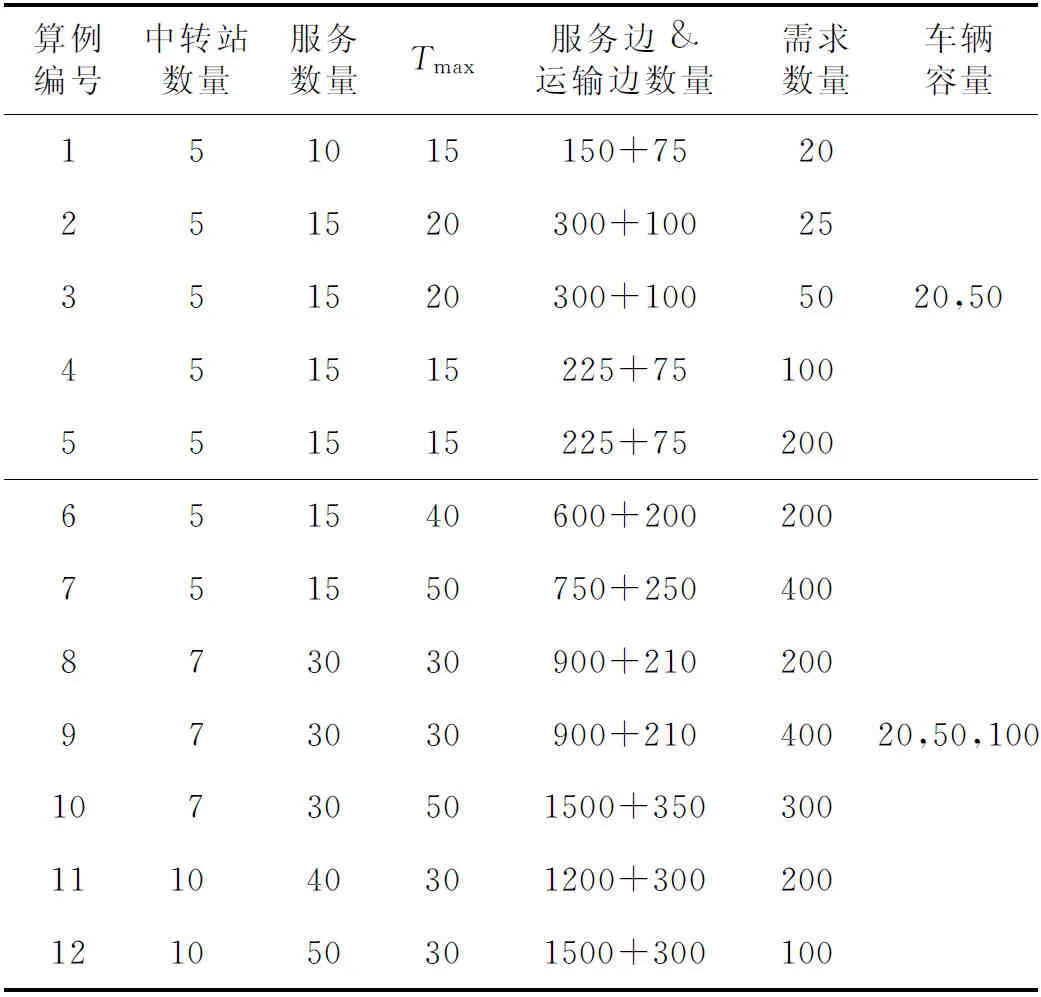
Table 3 Problem instance sizes

Table 4 Parameters values

4.2 小規模數據求解

針對小規模算例1～算例5，本文將所有可能的路徑變量枚舉出加入求解器CPLEX進行求解，并將其結果和分支定價算法的結果作對比。2種算法的求解時間限制均設置為2 h。分支定價算法中，按照節點的下界大小進行節點選擇，優先搜索下界最低的節點，有助于更快地找到小規模算例的最優解。割平面策略只應用在父節點進行分支操作后下界沒有提升的節點中，并且相應的約束會保留在當前節點。強化策略中，設置每求解10個節點使用一次強化策略，targetSize設置為1 000。表5展示了分支定價算法和求解器對小規模算例求解的結果。

在表5中，|θ|列表示所有可能路徑變量的數量，本文將該數量的路徑變量全部加入到求解器CPLEX中直接求解原MIP問題。由表5可看出，分支定價算法在5組算例中的4組找到最優解并證明了是全局最優。求解器CPLEX則在算例1和算例5中找到了最優解，然而對所有小規模算例都無法證明最優性。盡管在其他相關研究[4]中，求解器在提升下界方面有很好的表現，但在該問題中，相比于求解器，分支定價算法總是具有更佳的提升下界的表現。總體來說，在精確求解小規模問題方面，相比于求解器直接求解，分支定價算法在尋找可行解和提升下界方面都具有更好的表現。

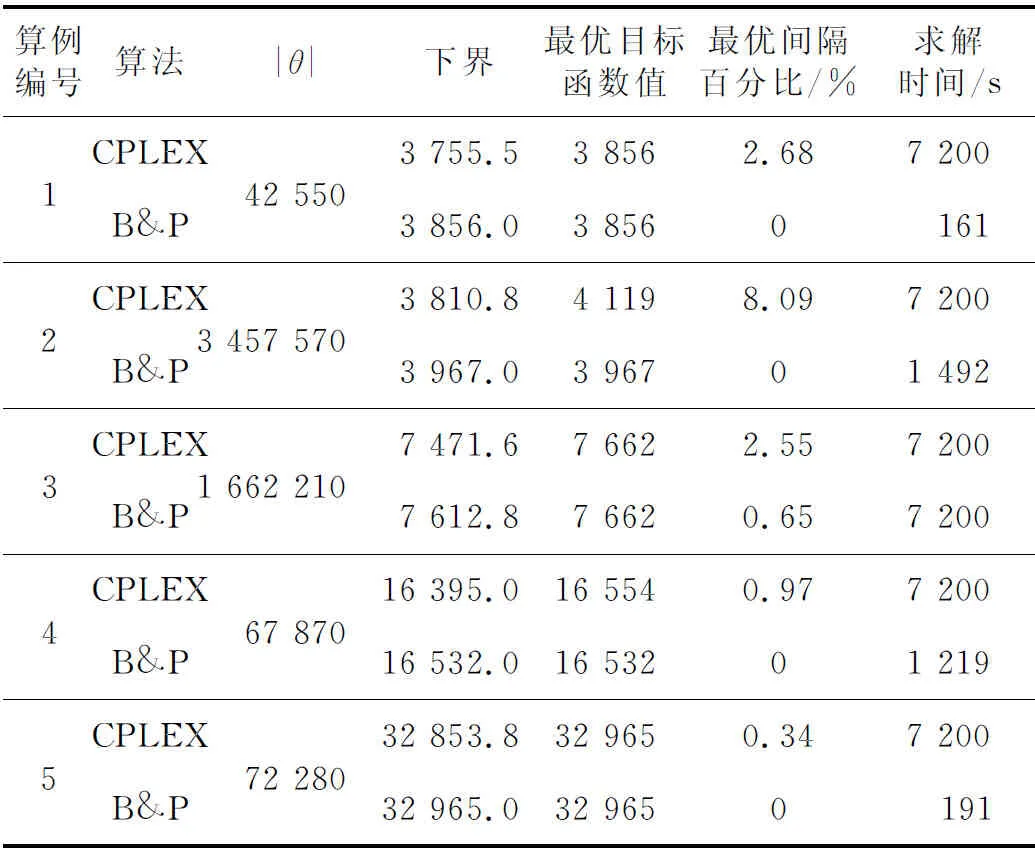
Table 5 Comparison of results on small instances of the branch and price algorithm and the CPLEX MIP solver

4.3 中等規模數據求解

在求解中等規模算例時，如果使用不加強化策略的分支定價算法，絕大多數算例甚至無法在2 h內找到任何一個可行解，該實驗事實表明了強化策略的必要性。為了進一步驗證分支定價算法結合強化策略的高效性，本文將其與效果表現良好的常用算法——基于列生成的啟發式算法進行比較。

使用分支定價算法和基于列生成的啟發式算法對算例6～12中共14組中等規模數據進行了測試，求解時間均為2 h。基于列生成的啟發式算法的主要思路是使用列生成算法對原問題對應的LP問題進行求解，并將求解過程中生成的所有路徑變量加入求解器，求解僅包含該部分列變量的MIP問題。在分支定價算法中，由于本文的求解目標不再是全局最優，有限時間內的最優解往往由強化策略搜索得到。強化策略中，本文設置每求解2個節點使用一次強化策略，targetSize設置為1 000。表6顯示了2種算法對中等規模數據的測試結果。

在表6中，強化策略|θ|表示獲得最優解時加入求解器中的路徑變量數。 基于列生成的啟發式算法中的|θ|列表示加入求解器中路徑變量數。在14組測試結果中，分支定價算法在12組數據上的表現都要優于基于列生成的啟發式算法。注意到由于算例10運營周期為50，2個算法在2 h之內無法對原問題的LP問題求得最優解，所以未顯示下界和最優間隔，僅對2個算法的最優解進行比較。另一方面，不同測試用例之間的最優間隔百分比的值相差較大，這主要和各部分成本之間的比例構成有關。由表6結果可以看出，相比于經典的基于列生成的啟發式算法，分支定價算法在中等規模問題上具有更好的表現，可以有效解決該規模的問題。

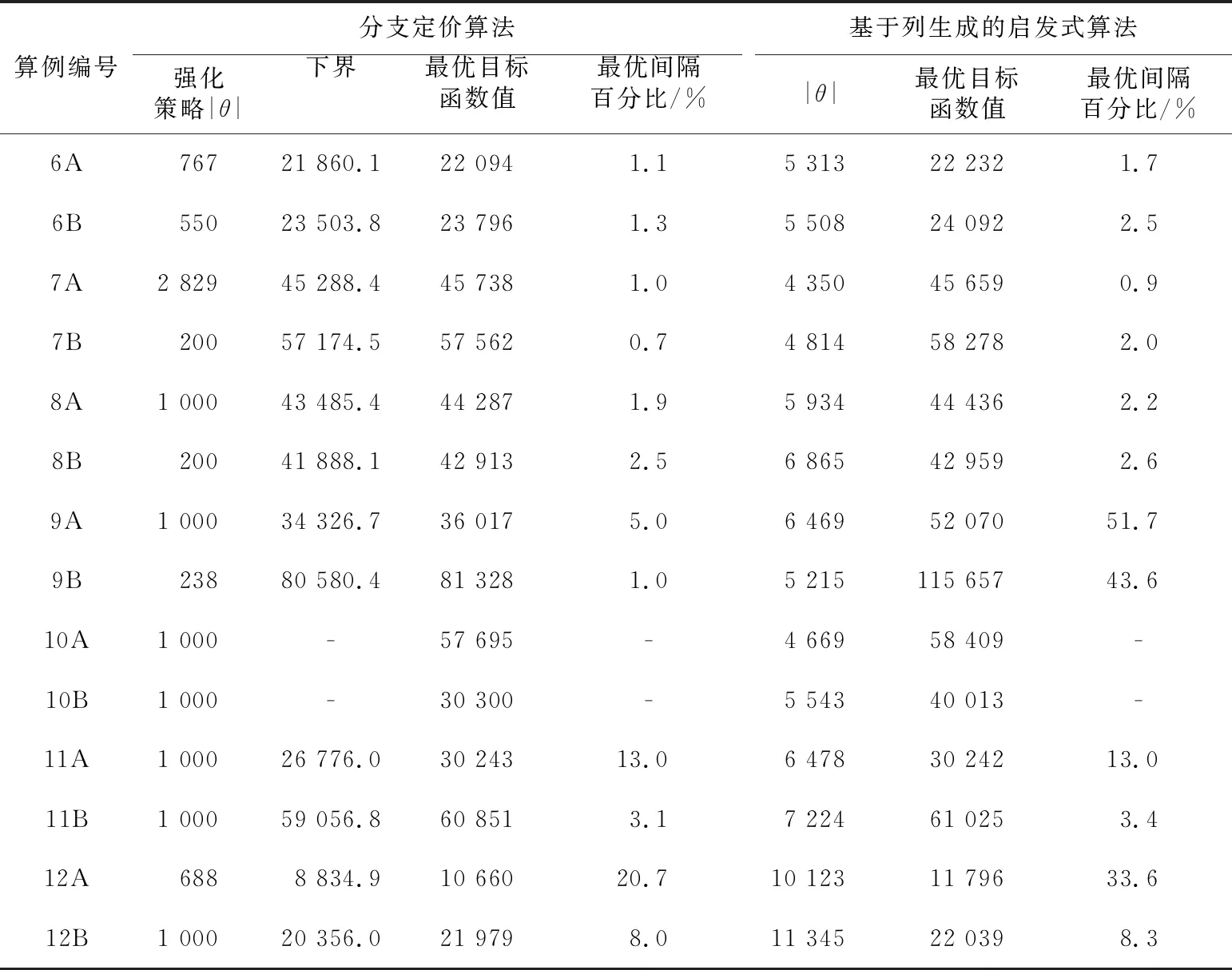
Table 6 Comparison of results on medium instances of the branch and price algorithm and the CG-based heuristic algorithm

5 結束語

本文針對電動汽車支持的鎮際快遞配送系統建立基于路徑變量的數學模型。模型構建在具有周期性的時空網絡之中，同時考慮到車輛資源、倉儲資源和充電樁資源的管理問題。本文針對該模型提出了分支定價算法。分支策略有利于削弱由時間離散化導致的對稱性問題，子問題中的標簽算法為列生成算法的主問題提供支持部分充電的電動汽車路徑變量。分支策略和割平面策略的組合有助于實現對小規模數據的精確求解。強化策略通過篩選路徑變量并利用求解器的高效性，幫助算法在求解中等規模問題時找到高質量可行解。實驗對比了分支定價算法和CPLEX求解器在精確求解小規模問題上的表現，以及與基于列生成的啟發式算法對比了在中等規模問題中的表現，結果表明了分支定價算法在精確求解和啟發式求解方面的高效性。因為在時空網絡上構建模型，時間離散化會造成問題規模的迅速擴增，加大問題的求解復雜度，后續的研究可以考慮探究上述問題在時空網絡的子網絡中實現精確求解的可能性[13]，以期擴大問題求解規模。