圖形的旋轉變換中的模型提煉與探究

倪秀靜

《義務教育數學課程標準（2011年版）》指出，在數學課程中，應當注重發展學生的數感、符號意識、空間觀念、幾何直觀、數據分析觀念、運算能力、推理能力和模型思想。

由此引發思考，可否借助幾何直觀把復雜的圖形變換問題變得簡明、形象，提煉出有助于探索解決問題的數學模型，引導學生找到這類問題的本質。

一、問題探究

我們先從例1的解法談起。

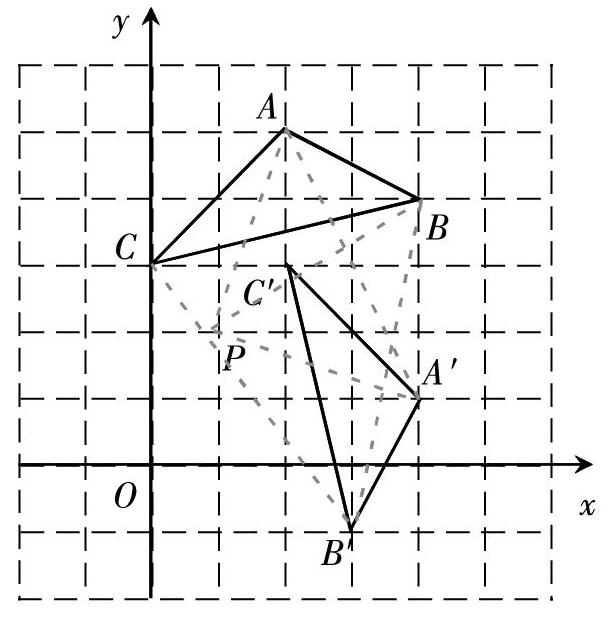
例1：如圖，將△ABC繞點P順時針旋轉得到△A′B′C′，則點P的坐標是?_______。

【分析】根據圖形旋轉的基本性質：一個圖形和它經過旋轉所得到的圖形中，對應點到旋轉中心距離相等，兩組對應點分別與旋轉中心連線所成的角相等。

先根據圖形可知點A的對應點為點A′，點B的對應點為點B′，再根據旋轉的性質得到旋轉中心在線段AA′的垂直平分線上，也在線段BB′的垂直平分線上，那么兩垂直平分線的交點即為旋轉中心。

【解答】解：∵△ABC繞P點順時針得到△A′B′C′，

∴點A的對應點為點A′，點C的對應點為點C′，

作線段AA′和CC′的垂直平分線，它們的交點為P（1，2），

∴旋轉中心P點的坐標為（1，2）.

二、提煉模型——讓“動”起來的圖形“靜”下來

通過例1，我們發現在解決這個問題的過程中，關鍵點是要抓住圖形旋轉的性質，即對應點到旋轉中心的距離相等，由此推斷出旋轉中心必在對應點連線AA′和CC′的垂直平分線上。那我們能不能進一步思考，如果我們將旋轉中心P和對應點連接起來，那么此時構成的三角形△PAA′、△PBB′、△PCC′會是什么性質呢？在旋轉的過程中，旋轉角可以用圖形中哪個角來表示呢？

【分析】根據圖形旋轉的性質可知PA=PA′，PB=PB′，PC=PC′

所以首先可以判定△PAA′、△PBB′和△PCC′是等腰三角形。

由旋轉的定義可知，此時旋轉角可以用∠APA′，∠BPB′，∠CPC′來表示。

因為旋轉圖形的整體性，所以圖形上每一個點繞P點的旋轉角度都相同。

即∠APA′=∠BPB′=∠CPC′

由圖可知此時∠CPC′=90°，∴∠APA′=∠BPB′=∠CPC′=90°

可以判定△PAA′、△PBB′和△PCC′是等腰直角三角形。

從這一分析過程，我們不難發現，在例1里，由于旋轉角為90°，所以對應點和旋轉中心構成的三角形不僅是等腰三角形，而且還是等腰直角三角形。這是由對應點到旋轉中心距離相等這一性質決定的。

那么這一結論，是不是也適用于其他旋轉的圖形呢？

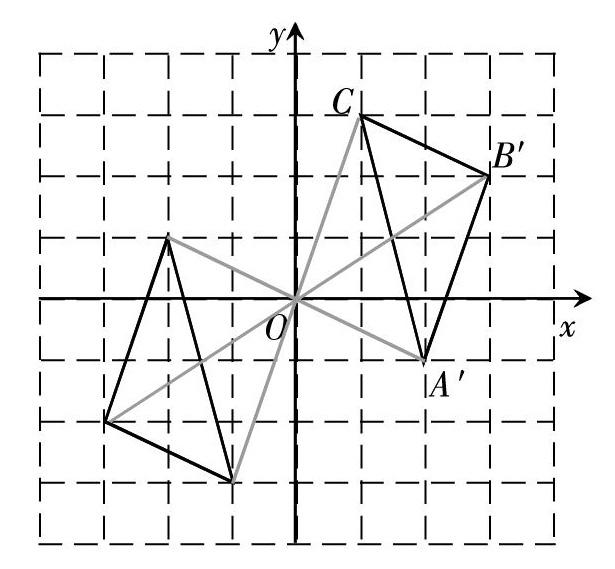
由之前的問題分析可知：對應點到旋轉中心距離相等這一性質始終存在，那么結論是否成立就取決于旋轉角度了。不難想象，如果旋轉角為180°時，這時兩個對應點和旋轉中心三點共線，是不能構成三角形的。由中心對稱的概念和性質可知，這時旋轉前后的兩個圖形成中心對稱，如圖。

而只要旋轉角度小于180°，這時這三點必可構成三角形，而這個三角形由旋轉的性質決定了其只能是等腰三角形。至于是什么樣的等腰三角形又取決于旋轉角（等腰三角形的頂角）的大小，即旋轉角（頂角）為90°時，為等腰直角三角形;旋轉角（頂角）為60°時，為等邊三角形。我們將該結論提煉為如下的模型：

三、模型應用

例2：如圖，在Rt△ABC中，∠ACB=90°，AC=5cm，BC=12cm，將△ABC繞點B順時針旋轉60°，得到△BDE，連接DC交AB于點F，求△ACF與△BDF的周長之和是多少。

【分析】根據模型思想，關注兩個對應點與旋轉中心構成的三角形△BCD。根據旋轉的性質可知旋轉角∠CBD=60°，BC=BD，則△BCD必為等邊三角形。再利用三角形周長定義得到△ACF與△BDF的周長之和=AC+CD+AB+BD，接著由△BCD為等邊三角形得到CD=BC=BD=12，于是就可以計算出△ACF與△BDF的周長之和。

例3：如圖，將Rt△ABC繞直角頂點C順時針旋轉90°，得到△A′B′C，連接AA′，若∠1=20°，則∠B的度數是? ? ? 。

【分析】根據旋轉的性質可得AC=A′C，然后判斷出△ACA′是等腰直角三角形，根據等腰直角三角形的性質可得∠CAA′=45°，再根據三角形的一個外角等于與它不相鄰的兩個內角的和求出∠A′B′C，然后根據旋轉的性質可得∠B=∠A′B′C。

【解答】解：∵Rt△ABC繞直角頂點C順時針旋轉90°得到△A′B′C，

∴AC=A′C，

∴△ACA′是等腰直角三角形，

∴∠CAA′=45°，

∴∠A′B′C=∠1+∠CAA′=20°+45°=65°，

由旋轉的性質得∠B=∠A′B′C=65°。

當然，解決圖形變換問題的方法還有很多。本文只是拋磚引玉，用意在引導學生找到問題本質，把復雜的圖形變換問題變得簡明、形象，從共性的條件中提煉模型，讓模型為自己所用，積累數學分析經驗，領略數學模型思想，激發學生學習數學的興趣和熱情。

參考文獻：

中華人民共和國教育部.義務教育數學課程標準（2011年版）[M].北京：北京師范大學出版社，2012.