小學數學教材專業化解讀背景下學生思維能力培養的策略研究

常州市龍城小學 巢紅開

教材是踐行數學新課標要求和落實教學活動的有效載體，還是學生濃縮學科知識以及建構知識體系的根本保障。過去，教師在數學教學當中存在著機械化利用教材的情況，也就是單純地照本宣科，而不能夠對教材內容進行深入挖掘和利用，影響到教材核心價值的發揮。隨著新課標的落實和對教師專業化解讀教材要求的提高，小學數學教師需要在積極用好教材的過程中，找到教材中有助于訓練學生思維的資源，同時抓住教材教學的有利契機，綜合推動學生的數學思維品質培養，確保數學教學的科學化和創新性發展。

一、小學數學教材專業化解讀概述

在課程改革思想的指導下，把過去的“教教材”轉變為如今的“用教材教”是利用教材的根本原則，也是教材專業化解讀的核心要求。解讀教材的重要目的是依托教材這一基本資源，挖掘其思想內涵以及方法，以便在教學實踐當中有效利用。小學數學教師要實現對教材的專業化解讀，必須把握以下內容：一是對教材內容的變化情況進行解讀，深層次理解教材內涵。對小學數學教材進行專業化解讀，首先應該做的就是梳理教材當中每個內容的變化情況，注意把某個知識點放置于這個單元和這個學段，甚至是整個知識體系當中進行全局審視和考量。隨著課程改革的深入，數學教材編排也發生了一定的變化，這樣的變化首先就體現在教材內容上，這些內容有增有減，也有一定的刪改。那么教師就需要在專業化解讀中把握教材發生的變化，尤其是要分析實質性改變以及出現變化的原因，以便掌握教材的內在意蘊。二是對教材編排情況進行全面梳理，掌握教材中形成的邏輯體系。在數學教材中，數學知識是由淺入深、逐層遞進呈現出來的，契合學生的認知規律，有助于學生邏輯思維的養成。在數學教材的專業化解讀當中，應該對教材的編排情況進行梳理，對教材知識邏輯體系的呈現情況進行分析，把握不同知識之間的內在關聯和不同教學階段的聯系。三是通過關注考量教材關鍵點，順利把握教材教學的重難點。數學教學當中，每個不同的模塊都有相應的關鍵點，而教材也對關鍵點進行了著重說明，那么教師在解讀當中就應該把握好教材當中的關鍵點，并將其作為教材教學當中的重難點，讓數學教學更清晰。

二、小學數學教學當中數學思維能力培養的作用與原則

數學思維能力的外在表現有很多，比如抽象概括能力、分類轉化能力、類比能力等。小學生年齡小，思想與思維都不成熟，處在邏輯思維的啟發和初步發展階段。在這一階段加大對學生數學思維能力的訓練，不僅能夠幫助學生突破學習難點，解決大量抽象化的數學問題，還能夠完善學生的知識體系，發展學生的邏輯體系，讓學生把思維能力內化為數學素養，最終促進綜合素質的發展。培養學生數學思維能力的原則主要包括：（1）以教材為基礎原則。注意把教材作為基本教學素材和教學設計的出發點，通過專業解讀教材，保證教學設計的有序性和科學性；（2）循序漸進原則。思維能力養成是不斷積累和長時間鍛煉的過程，所以整個過程應該有充足耐心，應該循序漸進，逐層深入，不能一蹴而就，更要避免操之過急帶來的不良影響；（3）靈活多變原則。教師在對學生進行思維訓練時，選擇的方法不能墨守成規、故步自封，而是要在契合學生身心特征的情況下，盡可能靈活多變和多樣，提高學生接受度。

三、小學數學教材專業化解讀背景下學生思維能力的培養策略

以蘇教版“平面圖形面積計算公式推導”為例。

1.利用教材例題推導長方形面積計算公式

在長方形面積計算公式的推導過程中，為了訓練學生的思維能力，同時用好教材專業化解讀的成果，需要從恰當利用教材給定例題著手，讓學生通過例題編排的分析循序漸進地投入公式推導過程，在不斷開放思維的過程中訓練思維能力。比如，教材的例題4是讓學生分組任意擺弄三個小正方形，之后填寫表格，沒有像下面的例題一般用卡通對學生進行思考方向指導。此時教師就需要根據此處的教材安排充分考慮擺長方形的目的，然后設計問題引領學生思考，比如：你有什么發現嗎？教師可以設計一個學習記錄單，讓學生記錄下自己的發現，比如包含幾個小正方形，那么長方形的面積就是幾平方厘米；橫排擺幾個長度就是多少厘米，豎排擺幾個寬度就是多少厘米。這些發現都是學生在完成例題給定任務之后獲得的，而教師也通過精心設計思考題，讓學生自覺歸納自己的發現，把認知引向深入。

2.借助教材解讀推導平行四邊形面積公式

在根據教材例題推導、總結了長方形面積公式之后，接下來就可以由此聯想到整個平面圖形面積計算公式。為了確保公式推導效果，教師需要采用以此類推的教學設計方法，把對教材內容專業化解讀的成果融入教學活動當中，以培養學生的數學素養。比如，平行四邊形面積公式推導如圖1。教材先讓學生分析以下每組兩個圖形面積是否相等，然后讓學生掌握轉化前后，雖然形狀發生了變化，但是面積沒有發生變化。接下來，要求學生嘗試把平行四邊形面積轉化成長方形，讓學生利用有效轉化的方法，結合長方形特征完成轉化任務。在教學最后，教師可以讓學生自主選擇一個平行四邊形，將其轉化成為長方形之后計算出圖形面積，并在小組溝通當中推導得到平行四邊形面積公式。

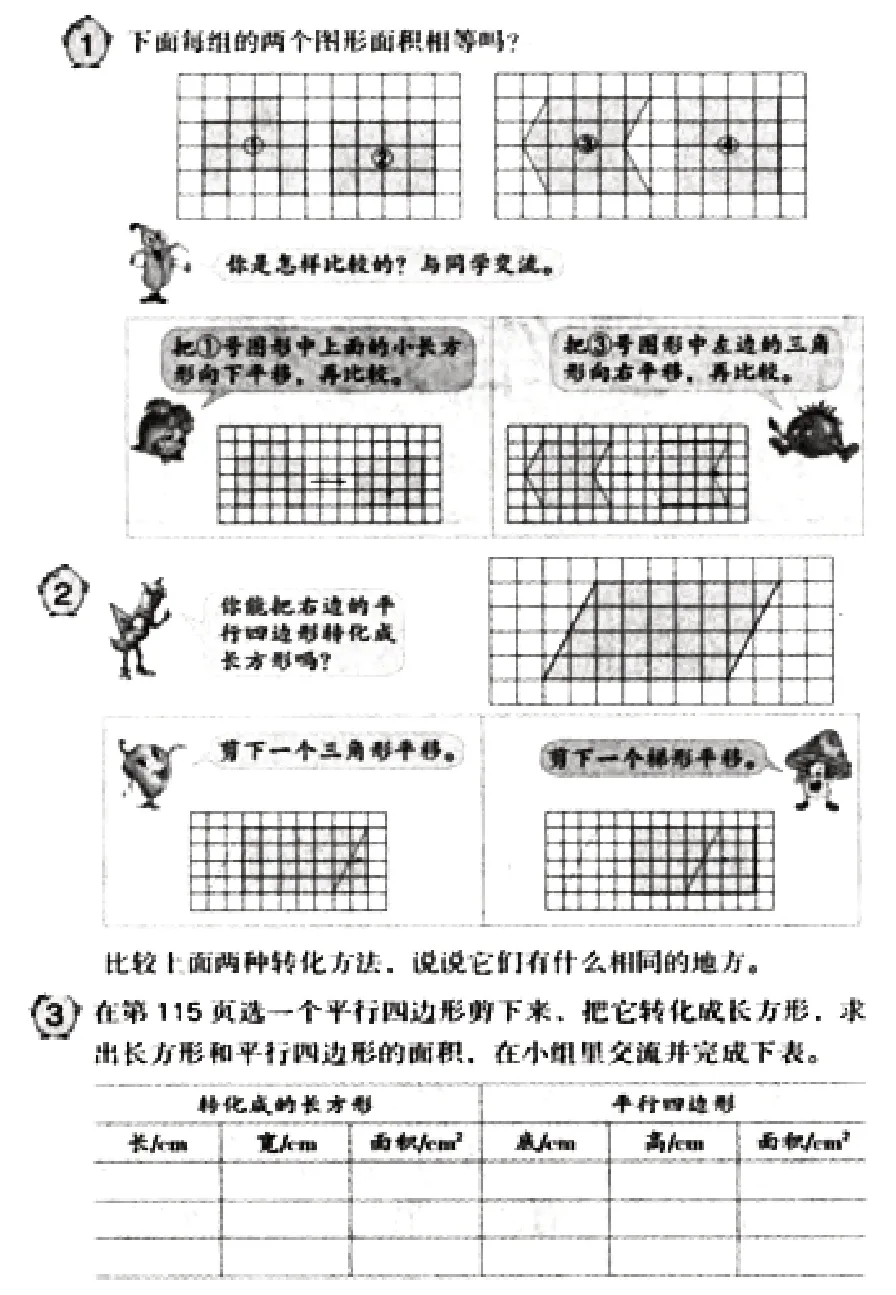
圖1

小組討論：

（1）轉化成的長方形與平行四邊形的面積相等嗎？

（2）長方形的長和寬與平行四邊形的底和高有什么關系？

（3）根據長方形的面積公式，怎樣求平行四邊形的面積？平行四邊形的面積=底×高

如果用S表示平行四邊形的面積，用a和h分別表示平行四邊形的底和高，上面的公式可以寫成：S=a×h。

3.延續類似結構推導圓的面積計算公式

在平面圖形面積公式的推導過程中，在研究了長方形以及平行四邊形之后，接下來需要推導和掌握的就是圓的面積計算公式。圓這個圖形和學生學習的其他平面圖形有著一定的差別，也在無形之中增加了學生的推導難度，但是通過運用類似推導的方法，能夠幫助學生突破學習難點，高效完成推導學習任務。首先是給出一個圓，讓學生嘗試用數方格的方式算出面積，并由此指導學生掌握數方格的技巧。其次是給出兩個大小不同的圓，讓學生數方格并填寫好表格，由此感悟圓的面積與半徑之間的關系。教師在提問當中著重讓學生討論圓面積和半徑之間的關聯，給學生的探究學習指引思路和方向。在這之后，教師可讓學生將圓等分成16、32、64等份，然后思考所拼成長方形和原來的圓形之間的關系，讓學生得到初步結論，認識到長方形的寬和圓的半徑相等，長方形的長是圓周長一半，最終歸納出圓面積計算公式，完成整個類比推導任務。

現如今，對教材進行專業化解讀已經成為提高小學數學教學質量、優化數學課程設計的必然選擇，在這樣的情況下，教師應該樹立正確的數學教育理念，深層次把握教材編寫意圖，利用教材編排高質量的教學方案，把握好各個細節，并把解讀教材獲得的成果應用到學生的數學能力培養當中，拓展學生的思維，強化學生的思維品質。