四激振器激勵下振動機械‐物料系統同步控制?

黃志龍，張眾超，楚樹坡，宋桂秋，張學良

（1.東北大學機械工程與自動化學院 沈陽，110819）（2.紹興文理學院機械與電氣工程學院 紹興，312000）（3.青島海洋科學與技術試點國家實驗室 青島，266237）

引言

同步理論在各個行業應用廣泛［1‐3］。Wen 等［4‐5］對振動同步理論進行了廣泛的拓展和應用，取得了重要成果。為了增加振動機械的輸出功率，研究人員從2 個激振器同步運動轉向多個激振器的同步運動研究。Zhang 等［6］研究了遠共振振動系統中3 個不相同的同向旋轉激振器的相位和速度自同步。Zhao 等［7］對4 個感應電機驅動的振動系統進行了同步理論研究。劉云山等［8］利用自同步方法對三激振器激勵下的振動同步傳動理論進行了研究。為了更加符合實際工況，激振器激勵振動機械的同步理論研究應考慮物料對振動系統的影響［4‐5］。因此，筆者研究了考慮物料影響的振動系統中4 個激振器的相位和速度同步。

隨著激振器數量的增加，采用控制理論解決同步問題是不錯的選擇。在許多同步控制的研究和應用中，自適應滑模控制算法被廣泛用于提高同步控制系統的魯棒性［9‐11］。Sun 等［12］通過交叉耦合和自適應方法控制多個運動軸的反饋位置誤差，實現了位置同步。Kong 等［13］通過主從控制策略和自適應滑模控制算法研究了線性振動系統中4 個激振器的同步控制。為了提高振動機械系統的同步精度，筆者針對振動機械‐物料系統中4 個激振器的同步控制問題建立了新的控制系統。控制系統采用相鄰交叉耦合控制策略和自適應全局滑模算法，考慮了相鄰激振器之間的耦合特性。

筆者研究了振動機械‐物料系統中4 個激振器的轉速和相位的相鄰交叉耦合同步控制。首先，推導了4 個激振器激勵下的振動機械‐物料系統動力學模型；其次，考慮到振動機械‐物料系統中4 個反向旋轉激振器之間存在耦合動力學特性，建立了相鄰交叉耦合策略控制器；然后，通過Lyapunov 理論證明了所提出的控制器的穩定性；最后，通過數值模擬進一步驗證了提出的控制器能夠有效控制振動機械‐物料系統。

1 振動機械‐物料系統的動力學模型

圖1 為給出了考慮物料影響的四激振器激勵振動系統的數學模型。4 個激振器對稱分布，激振器1和4 逆時針旋轉，激振器2 和3 順時針旋轉。在系統的質心平衡點取Oxy坐標，系統有3 個自由度，即x，y方向和繞質心擺動方向ψ。當非線性振動系統中4個激振器的速度和相位分別相同時，實現y方向上的線性振動軌跡，消除了x方向的振動和ψ方向上的擺動。取y振動方向和水平方向的夾角δ為振動方向角，Fm和Fm分別為物料在x和y方向上對振動機體的非線性作用力。

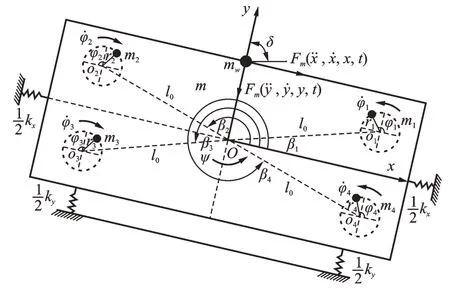
圖1 四激振器驅動非線性振動系統的數學模型Fig.1 Mathematic model of nonlinear vibration system driv‐en by four exciters

利用拉格朗日方法建立了4 個激振器驅動非線性振動系統的微分方程

其中：rj為激振器的偏心距離，rj=r，j=1，2，3，4；l0為振動機體的質心和激振器回轉中心之間的距離；δ為振動方向角；M為非線性振動系統的總質量，M=m+mj+kw mw；m為振動機體的質量；mj為激振器的質量；mw為物料的質量；kw為物料的結合系數；J為振動系統的轉動慣量；Jp為機體的轉動慣量；le為振動系統的等效轉動半徑；Jj為異步電機的轉動慣 量，Jj≈mjr2；fj為異步電機的阻尼系數；Tej為 異步電機的電磁轉矩。

Fm和Fm分別為物料作用在x和y方向的非線性力［14］

其中φd，φz分別為物料顆粒開始拋擲運動時的振動相角和物料顆粒拋擲運動結束時的振動相角；分別為物料顆粒下落時在y方向上的速度和此時振動機體在y方向上的速度。

在非線性振動機械‐物料系統中4 個異步電機的磁鏈方程［15］為

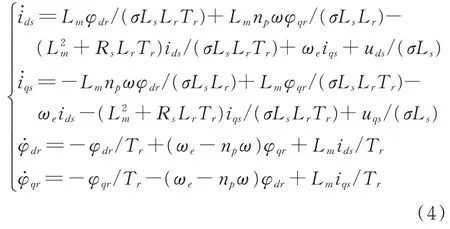
電磁轉矩方程為

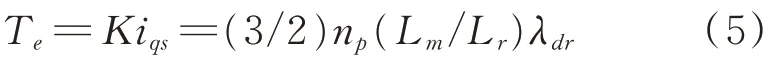
將式（5）代入式（1）中，通過控制非線性振動機械‐物料系統中4 個異步電機的轉矩電流實現4 個反向回轉激振器的同步運動。當4 個異步電機的轉速和相位實現同步時，非線性振動機械‐物料系統只能實現y方向上的直線振動軌跡，消除了x方向上的運動和ψ方向上的擺動運動。因此，考慮到物料影響的振動系統的同步控制問題轉化為由具有非線性負載轉矩的感應電動機驅動的4 個激振器的速度和相位同步控制問題，狀態方程可以簡化為

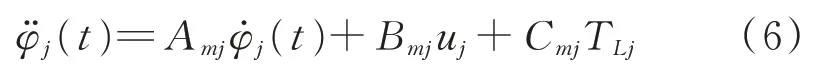
其 中：Amj=-fj/Jj；Bmj=Kj/Jj；Cmj=-1/Jj；uj為電機的輸入轉矩電流。

考慮到系統的外部負載擾動，式（6）可寫成

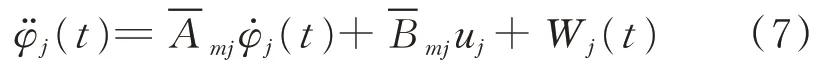
2 反向回轉四激振器相鄰交叉耦合控制策略

采用相鄰交叉耦合控制策略對4 臺反向回轉的異步電機進行控制，可以實現相鄰兩臺電機耦合形成耦合環，既考慮了兩個相鄰電機之間的交叉耦合特性又降低了控制系統的復雜程度。采用相鄰交叉耦合控制對4 臺反向回轉的異步電機的轉速和相位差進行控制，從而實現4 個反向回轉的激振器的同步運動。首先定義第j臺電機的轉速和相位跟蹤誤差分別為=ωj(t)-ωd(t) 和ej(t)=φj(t)-φd(t)，其中ωj(t)和ωd(t)分別表示第j臺電機的參考轉速和實際輸出轉速。非線性振動系統中異步電機跟蹤誤差應該滿足

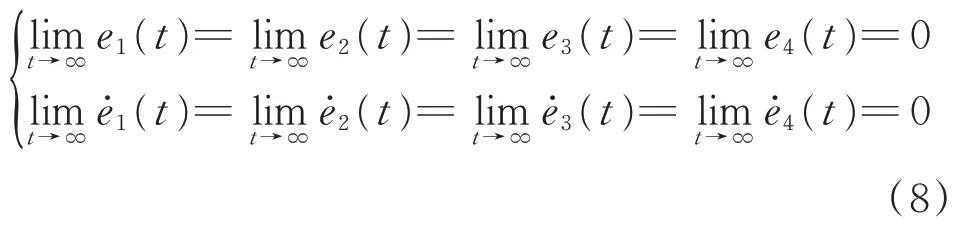
在相鄰交叉耦合控制策略中，同步誤差將通過補償模塊分別對相鄰電機和受擾動電機本身形成反饋。對系統中4 個反向回轉的電機的同步誤差應該有

如 果νj(t)=0 和=0（j=1，2，3，4）成 立，則式（8）成立，從而實現非線性振動機械‐物料系統中4 個反向回轉異步電機的同步控制目標。在此定義電機的相位耦合誤差和電機的轉速耦合誤差為

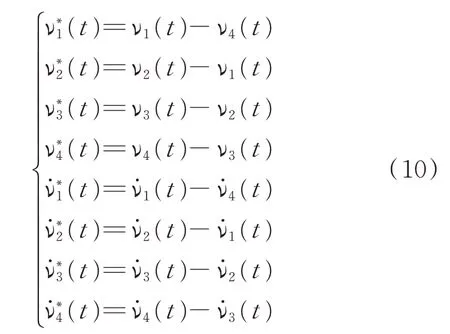
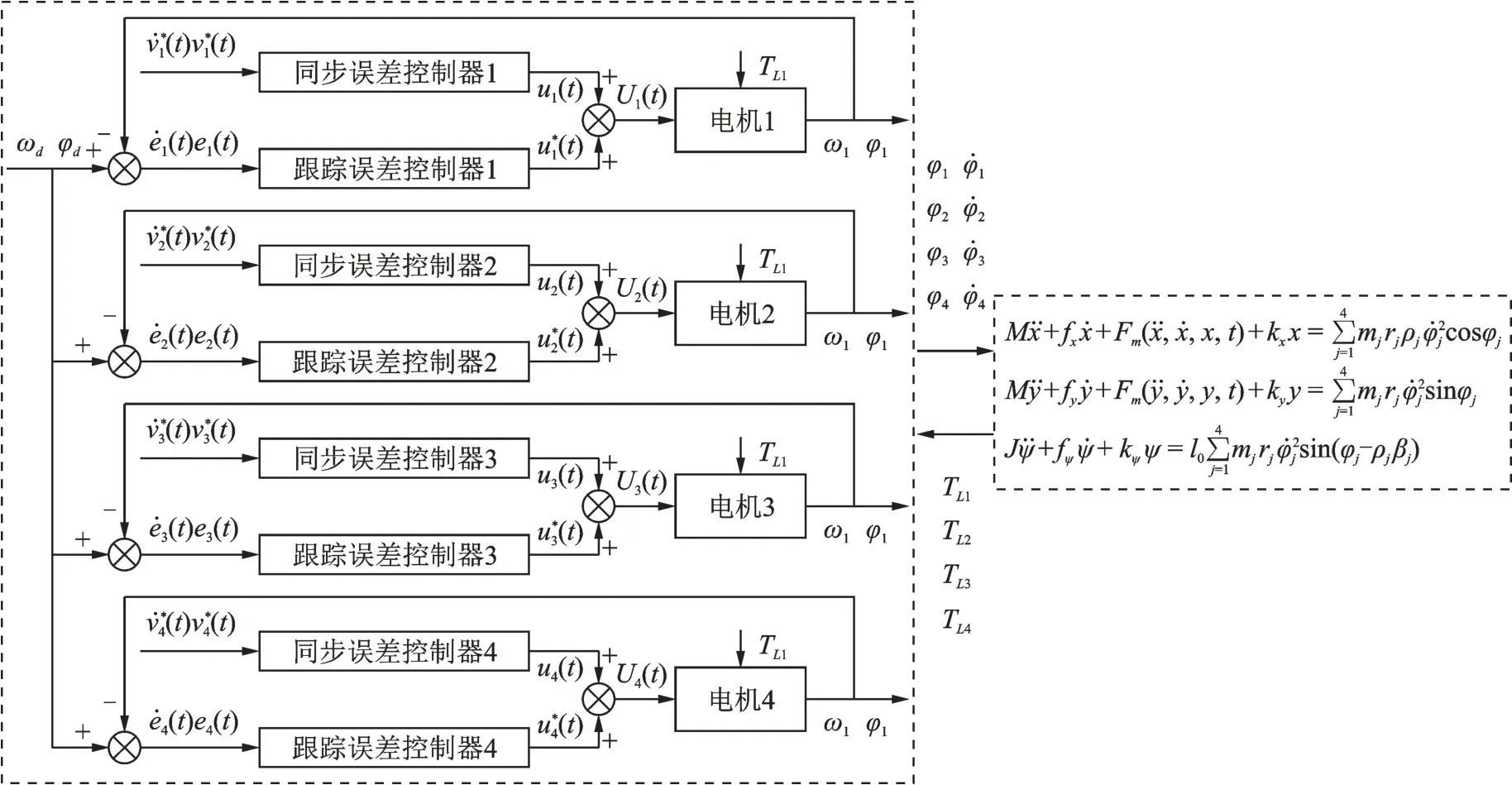
圖2 反向旋轉感應電機的相鄰交叉耦合控制框圖Fig.2 Adjacent cross-coupling control block diagram of reverse-rotation induction motors

3 四激振器相鄰交叉耦合控制器的設計

將非線性振動機械‐物料系統的相鄰交叉耦合控制器設計為跟蹤誤差控制器和同步誤差控制器兩部分。

3.1 跟蹤誤差控制器設計和穩定性分析

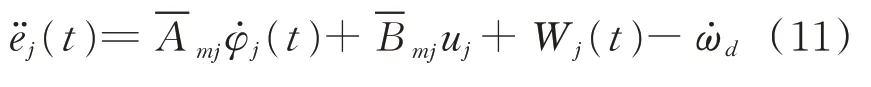
其中：Wj(t)≤σj為非線性振動機械‐物料系統總不確定性。

跟蹤誤差全局滑動變量為

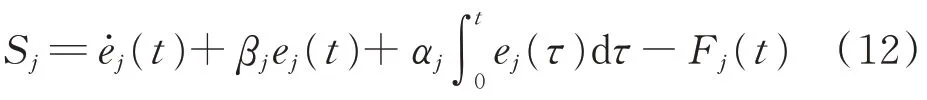
其中：αj和βj為正的常數。

全滑模因子F(t) 具有一階導數并且(t)=0，當滿足式（12）時有

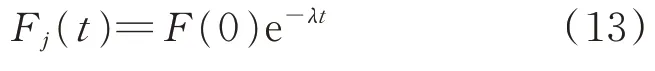
其中：λ為非常小的正常數。

由式（11）～（13）可知，對Sj求導后可以得到

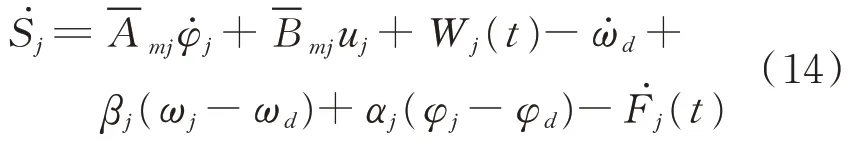
設計等效控制率為

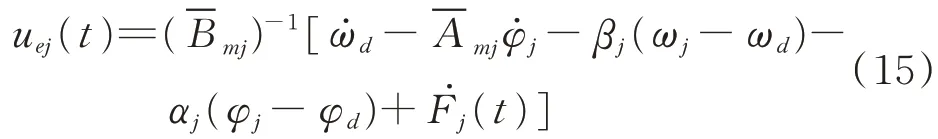
設計魯棒控制器為

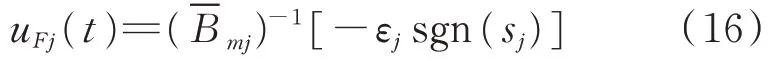
由式（15）和式（16）可以得到非線性振動機械‐物料系統中4 個反向回轉激振器的跟蹤誤差控制律為

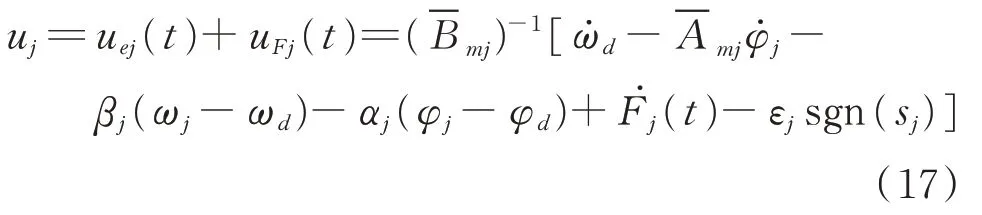
其中：j=1，2，3，4。

穩定性與有效性分析如下。

定理1如果εj>σj（j=1，2，3，4）成立，則有跟蹤誤差控制律方程（17）使4 個反向回轉激振器的轉速和相位跟蹤誤差軌跡限制在跟蹤誤差滑模面上，并且控制系統漸進穩定。

證明1

求導可得

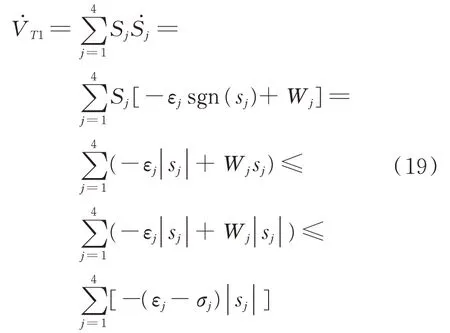
當εj>σj成立，則有<0 成立。根據Lyapu‐nov 穩定性定理，具有4 個反向回轉的激振器的跟蹤誤差控制系統是漸近穩定的，因此可以得到=0，對式（12）求導后代入=0，可以得到

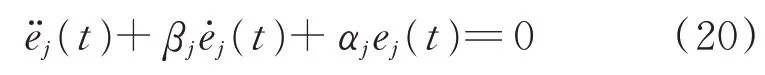
因為αj和βj都是正的常數，方程滿足Hurwitz條件。可以得到=0 和=0（j=1，2，3，4）。

3.2 同步誤差數學模型和穩定性分析

基于相鄰交叉耦合控制策略，設計出4 臺異步電機相位和轉速同步誤差的數學模型。異步電機的相位和轉速同步誤差滑動面j（j=1，2，3，4）為

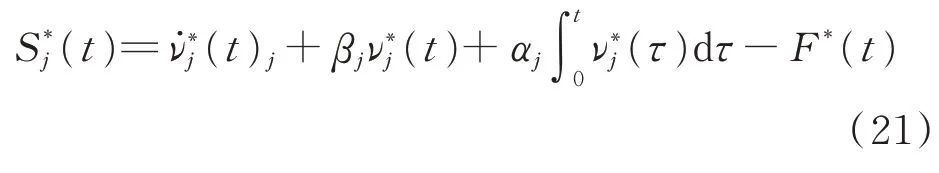
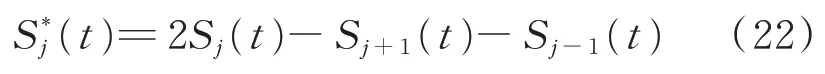
其中：Sj(t)為第j個激振器的轉速和相位跟蹤誤差滑動面。

將反向回轉激振器的轉速和相位同步誤差控制律設計為

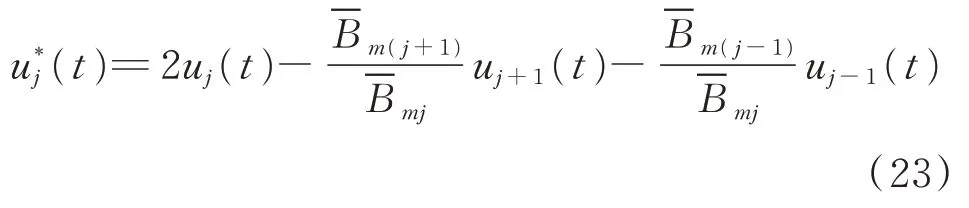
穩定性與有效性分析如下。

定理2如果εj>σj（j=1，2，3，4）成立，非線性振動系統中4 個反向回轉的異步電機的速度和相位同步誤差控制器可以在控制速率式（23）控制下穩定在滑動面上，因此系統漸進穩定。

證明2結合式（22），可以得到為

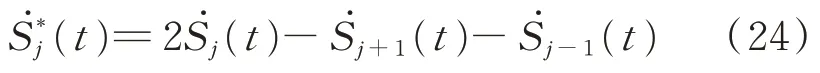
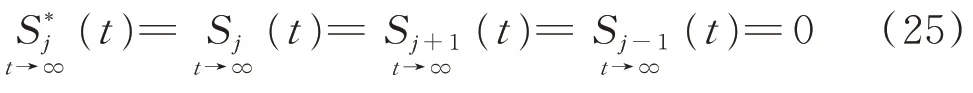
因此，非線性振動機械‐物料系統中4 個反向回轉激振器的跟蹤誤差控制器和同步誤差控制器能夠使激振器的轉速和相位實現同步，可以得到全局滑模控制律為

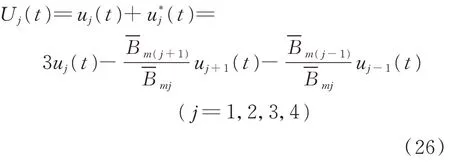
3.3 自適應算法和全局穩定性分析

由于振動機械‐物料系統的高度非線性和時變特性，激振器所承受的非線性時變負載轉矩很難確定。因此，采用自適應方法來調整開關增益εj（j=1，2，3，4）可以得到更好的控制效果，設計εj為

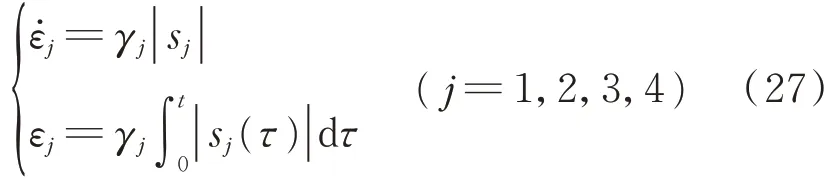
其中：γj為正值的自適應增益。

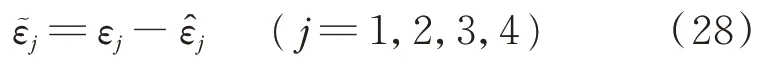
全局穩定性證明如下，Lyapunov 正定函數定義為

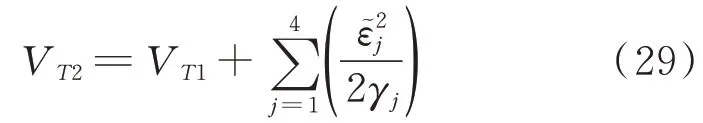
對式（29）求導可得

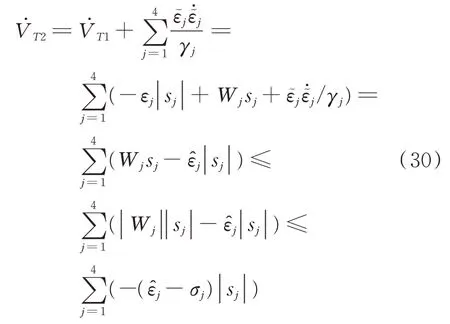
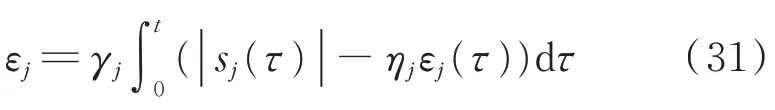
其中

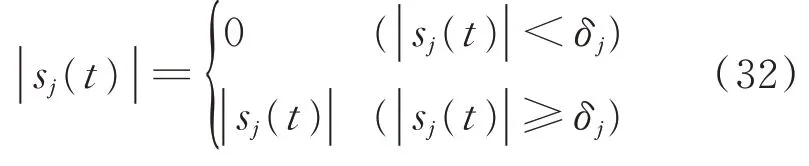
其中：ηj和δj為小的正常數。

將提出的相鄰交叉耦合控制器使用飽和函數sat（sj）代替符號函數sgn（sj）能更好地抑制抖振現象

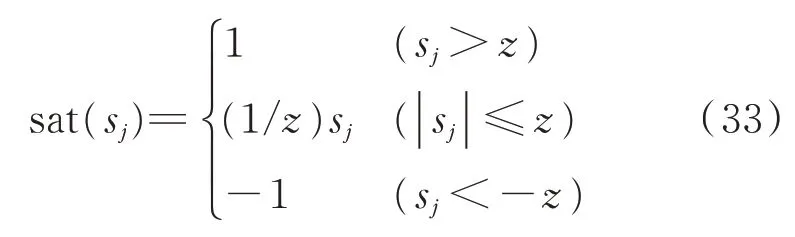
其中：z為一個大于零并且非常小的值。

修改后的控制律為

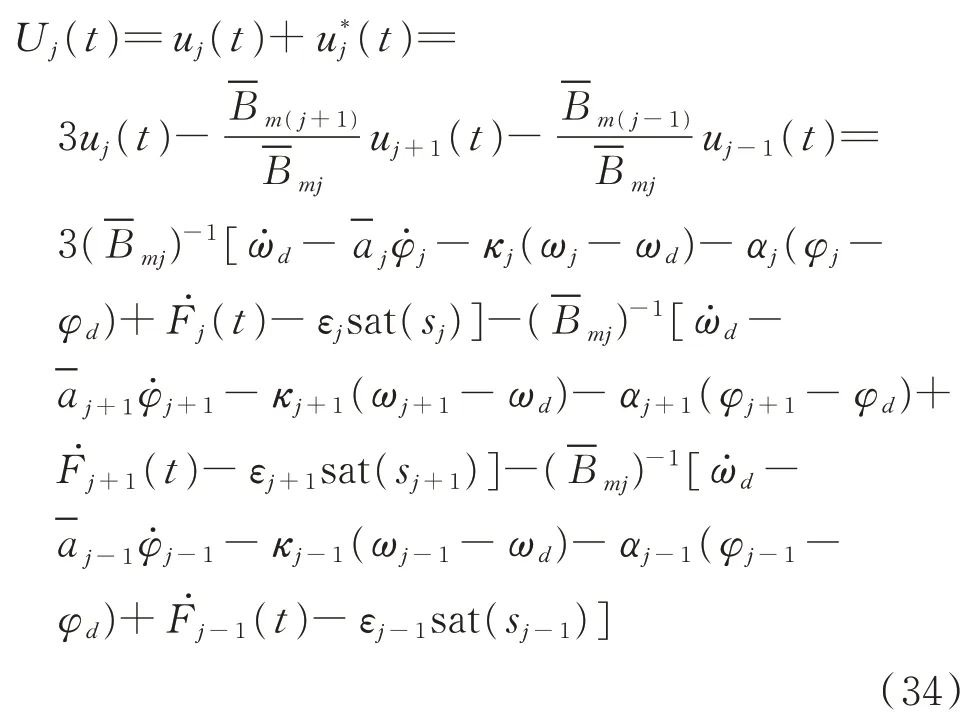
4 仿真分析

所提出的相鄰交叉耦合控制器由Matlab/Simu‐link 模擬。使用相鄰交叉耦合控制器來控制非線性振動機械‐物料系統，以說明非線性振動系統的特性，并討論和分析了非線性振動機械‐物料系統物料參數變化對相鄰交叉耦合控制系統的影響，以反映所提出的相鄰交叉耦合控制器對非線性振動系統的有效性。振動機械‐物料系統和控制系統的相關參數如表1 和表2 所示。

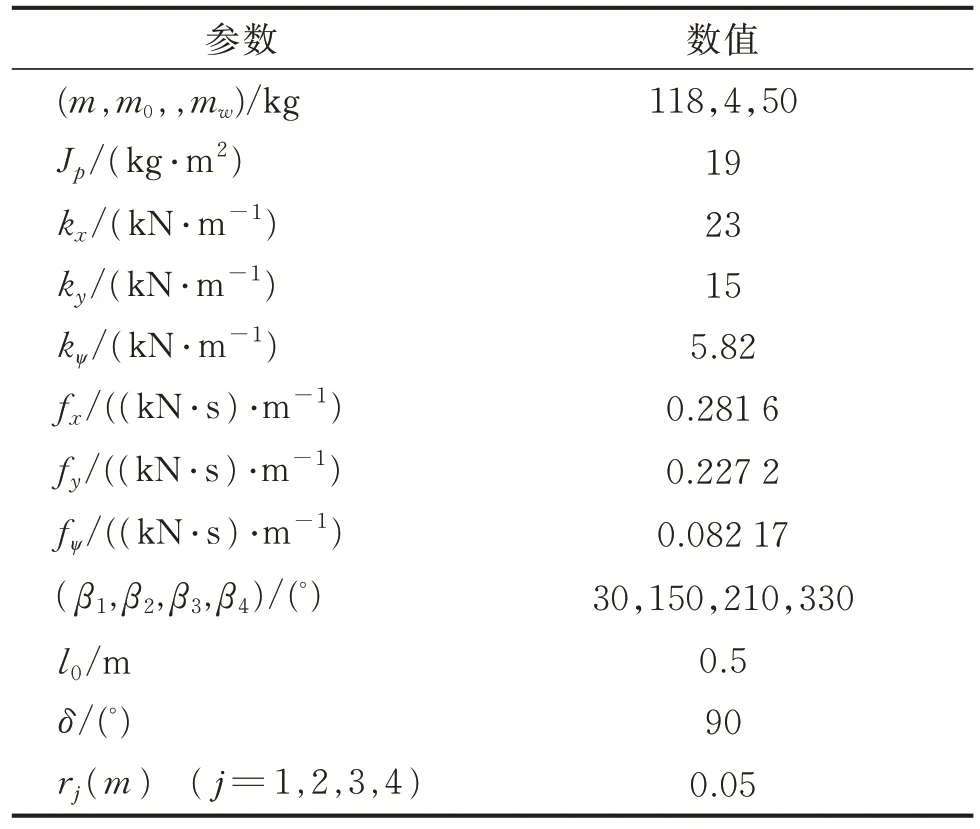
表1 振動機械‐物料系統的參數Tab.1 Vibration machinery‐material system parame‐ters

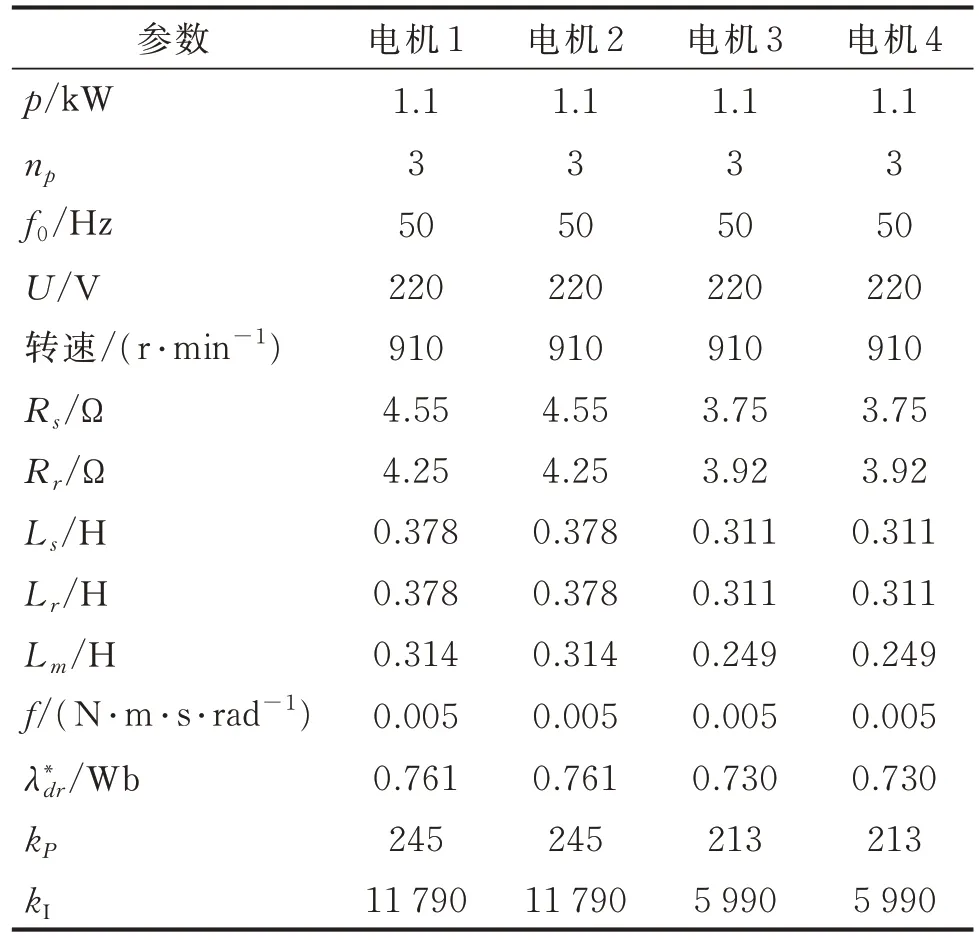
表2 4 個異步電機和控制系統的參數Tab.2 Parameters of four asynchronous motors and control systems

采用提出的相鄰交叉耦合控制器控制考慮物料非線性力的4 個激振器激勵振動機械系統。仿真分析的結果如圖3 所示。由圖3（a）可以看出，4 個異步電機的轉速在啟動階段和穩定階段的同步效果較好，啟動階段無轉速超調，穩定階段的轉速波動較小。由圖3（b）可以看出，4 個異步電機相互之間的相位差曲線在啟動階段出現波動，由于系統受到物料非線性力作用，系統穩定后相位差小幅增大但仍然在零附近波動。由圖3（c，d）可以看出，系統能夠在y方向上產生穩定的直線振動軌跡，消除了x方向的振動，并且ψ方向上的擺動運動在穩定后很小。這說明在相鄰交叉耦合控制器的控制下，4 個激振器激勵非線性振動機械‐物料系統能夠滿足實際要求實現穩定振動軌跡。從上述分析可以看出，由于相鄰交叉耦合控制器在控制過程中同時考慮了跟蹤誤差和相鄰電機之間的同步誤差，因此可以有效地控制考慮物料影響的振動機械系統，以達到所需要的直線振動軌跡。針對四激振器激勵下非線性振動系統提出的相鄰交叉耦合控制器提高了控制精度，合理地降低了控制系統的復雜性。

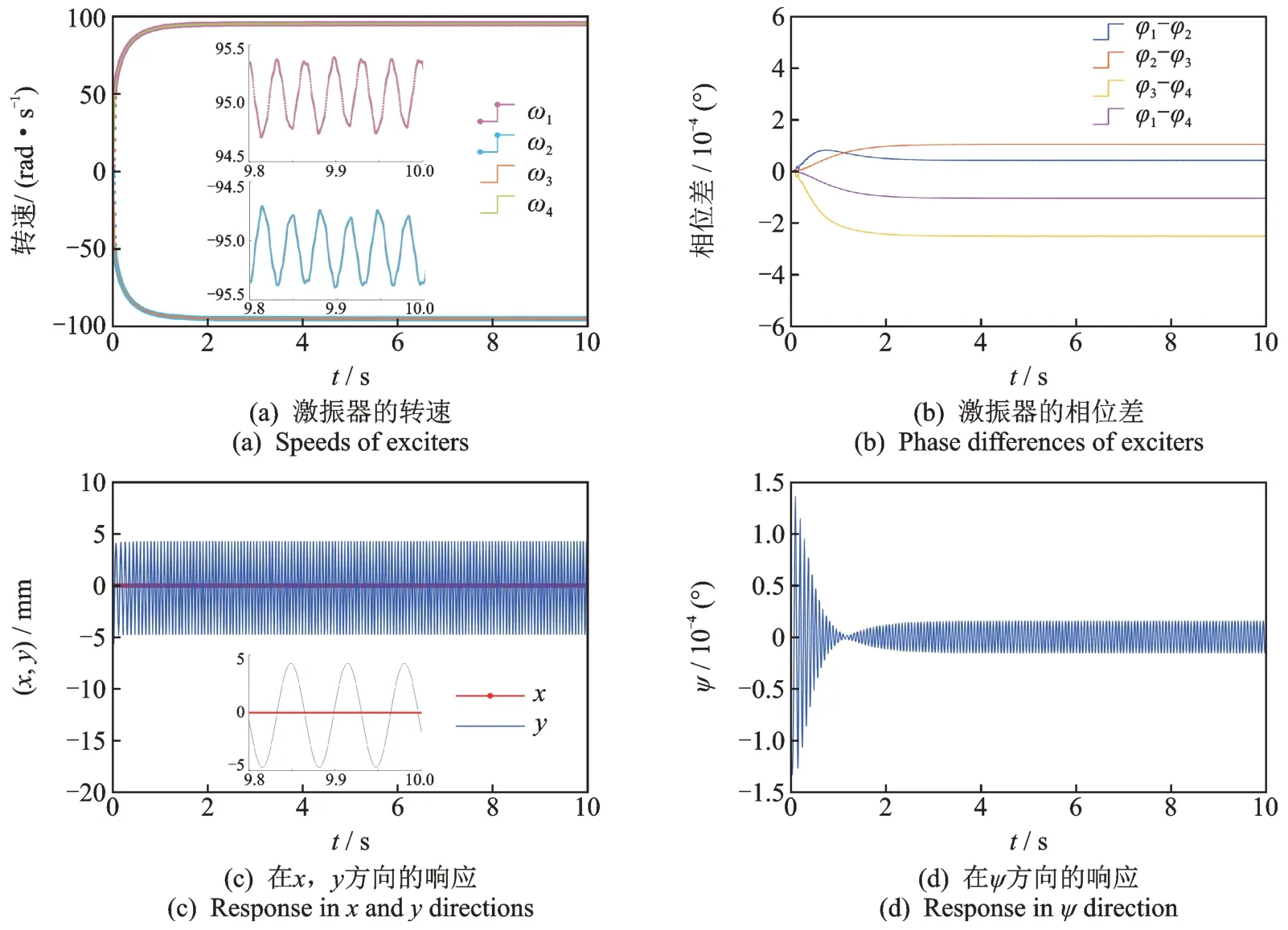
圖3 考慮物料影響的系統同步性能Fig.3 Synchronization performance of system considering the influence of material

由于在實際工程中，物料質量在振動系統運行期間會發生變化，下面分析當物料質量發生變化時對相鄰交叉耦合控制器的性能影響。當第5s 時物料質量從50 kg 變為30 kg，其他參數保持不變，討論此時對相鄰交叉耦合控制器同步性能的影響。如圖4（a，b）所示，在相鄰交叉耦合控制器的作用下，4 個激振器的轉速和相位處于同步運動狀態，物料的變化對轉速和相位同步運動沒有影響，并且相位差一直在零附近波動。如圖4（c，d）所示，非線性振動機械系統在y方向上的振幅隨著物料質量的減小而增大，并且系統在物料發生變化后仍然可以在y方向上形成有效的直線振動軌跡，x方向和ψ擺動方向的振動很小，表明系統的響應是穩定的。如圖4（e，f）所示，由于物料的變化，輸出轉矩隨負載轉矩減小而變化。可以看出，當物料變化時，相鄰交叉耦合控制器可以控制系統中4 個激振器在上述干擾條件下實現同步運動，這與前面的理論分析一致，4 個激振器中激振器1 和激振器4 沿逆時針方向旋轉，激振器2和3 沿順時針旋轉。反向回轉的激振器相互抵消x方向上的作用力，相互疊加y方向作用力。當4 個激振器的轉速和相位都處于同步狀態時，在y方向產生穩定的直線振動軌跡，消除x方向振動和ψ方向的擺動運動。綜上所述，針對4 個激振器激勵下的振動機械‐物料系統所提出的相鄰交叉耦合控制器能夠抑制物料參數變化對系統同步性能的影響。相鄰交叉耦合控制器對4 個激振器激勵下的振動系統具有良好的控制性能，并且提高了控制精度。

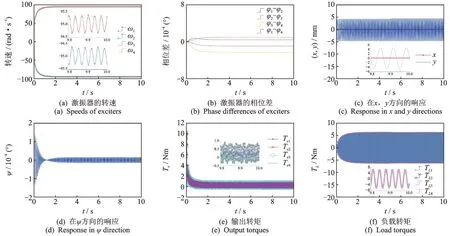
圖4 物料質量變化對相鄰交叉耦合控制器的影響Fig.4 The influence of material mass changes on adjacent cross-coupling control controller

5 結論

1）推導了考慮物料影響的4 個反向回轉激振器激勵下的振動機械系統動力學模型，針對非線性振動機械‐物料系統中4 個反向回轉激振器的轉速和相位同步問題，建立了自適應全局滑模算法和相鄰交叉耦合控制策略結合的控制器。

2）通過相鄰交叉耦合控制器對非線性振動機械‐物料系統中4 個反向回轉激振器的控制，非線性振動系統實現了穩定的直線振動軌跡。相鄰交叉耦合策略考慮了相鄰激振器之間的耦合作用，提高了4 個反向回轉的激振器轉速和相位的控制精度。自適應全局滑模算法能夠對非線性振動系統的總不確定性進行自適應逼近，使系統的響應更加平穩。

3）由于系統中存在非線性力的影響，使4 個反向回轉異步電機受到復雜的非線性時變負載轉矩，但在相鄰交叉耦合控制器的作用下系統仍然實現了穩定的振幅。通過分析非線性振動機械‐物料系統中物料參數變化對相鄰交叉耦合控制器的影響，進一步驗證了控制器控制非線性振動系統的有效性。