動靜摩擦因數對推焦系統動力學特性的影響?

陳俊君，李 駿，孫桓五，段海棟

（1.山西大學自動化與軟件學院 太原，030013）（2.太原理工大學機械與運載工程學院 太原，030024）（3.東北大學機械工程與自動化學院 沈陽，110819）

引言

大多數機械系統中都存在著摩擦引起的振動和噪聲現象［1］，包括汽車制動系統、齒輪嚙合系統、絲杠傳動系統等常用的機械裝置［2‐4］。機械裝置摩擦接觸面間產生的振動會導致接觸界面的磨損和破壞，在某些情況下甚至會導致機械系統的失效。焦爐推焦裝置的功能是將焦爐中成熟的紅焦從炭化室中推出，推焦桿通過滑履與炭化室地面接觸，在推焦作業過程中滑履與地面之間會產生強烈的摩擦，導致推焦裝置產生復雜的振動。該振動一方面會引起噪聲污染，另一方面也會加劇部件的疲勞和磨損，致使推焦系統的穩定性變差并且出現黏滑運動現象。穩定性變差指在工作過程中推焦裝置的重心位置發生較大的改變，工程中表現為裝置的垂直方向跳動和左右搖擺現象。黏滑運動指推焦裝置在行進過程中出現的速度忽快忽慢的現象，表現為推焦裝置的低頻顫振。建立動力學模型［5‐6］是研究摩擦自激振動系統不穩定性及黏滑運動的一個重要手段，而且有助于設計控制器來消除系統的不穩定性和黏滑運動。目前，已經建立了一些摩擦自激振動模型用來解釋不同的摩擦現象，如預滑動位移模型、Stribeck摩擦效應模型、黏滑運動模型和滯回效應模型［7］。預滑動位移模型主要描述靜態階段發生的微觀運動。在系統處于穩定的低速狀態下，摩擦力隨相對速度的增加先減小后增大，摩擦力的這種下垂特性稱為“Stribeck 摩擦效應”。一般情況下，在系統處于穩定狀態下滑動摩擦力的數值是單值的；而在滑動速度振蕩的非穩定狀態下則是多值的，并且摩擦力響應曲線在減速和加速階段具有不同的路徑。在滑動狀態下，遲滯環也稱為摩擦記憶遲滯環，根據相對加速階段摩擦力是否大于相對減速階段的摩擦力，可以分為順時針方向［8］和逆時針方向［9］兩種形式。到目前為止，還沒有通用的理論模型能夠完全解釋摩擦引起的振動現象。推焦作業過程屬于一種典型的滑動摩擦，對于焦爐推焦系統還存在著動力學模型缺乏、振動理論的研究不夠深入等問題［10］。因此，研究推焦系統的振動機理具有很強的理論和工程應用價值。

1 焦爐推焦自激振動系統建模

推焦裝置是將炭化室內的紅焦推出炭化室的具體執行機構，其主要結構包括推焦桿、齒輪齒條傳動機構、滑履、支棍和推焦頭。推焦裝置的具體結構如圖1 所示。其中，推焦桿是推焦裝置的核心構件，筆者研究的6.25 m 搗固焦爐設備中推焦桿的重量約為40 t，長為27 m，寬為0.34 m，高為1.05 m。根據推焦系統的實際工作情況，筆者建立了一個兩自由度的摩擦自激振動力學模型，如圖2 所示。傳送帶以恒定速度v0向單一方向移動，傳送帶上有一滑塊m，該滑塊受到恒定的法向力N作用，在豎直方向通過兩個線性彈簧k1和k2連接到豎直位置的固定端，在水平方向通過阻尼c和彈簧k3將其連接到水平位置的固定端，滑塊和帶之間的摩擦力F為滑塊提供驅動力。

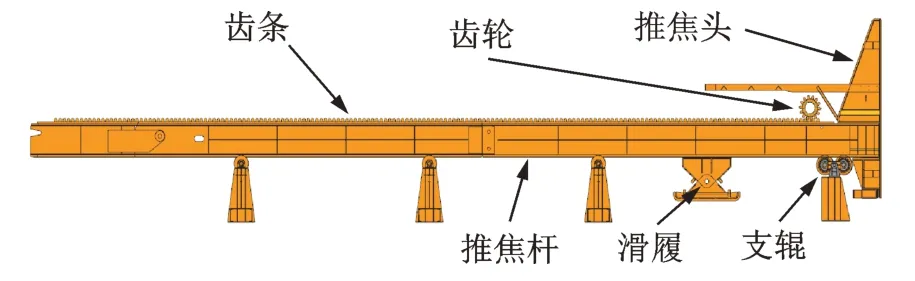
圖1 推焦裝置結構示意圖Fig.1 The schematic diagram of the coke pushing device

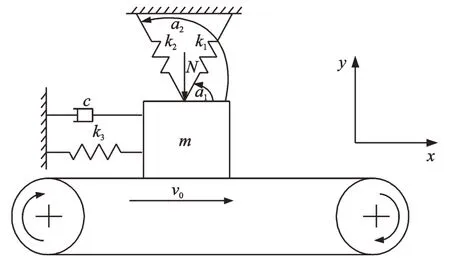
圖2 推焦系統的力學模型Fig.2 Mechanical model of the coke pushing system

該模型的運動微分方程可由式（1）給出

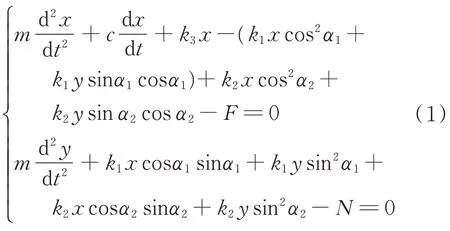
其中：F為作用在滑塊上的摩擦力。

使用式（2）的Stribeck 摩擦模型［11］進行計算，F定義為

其中：vr=表示滑塊與傳送帶之間的相對滑動速度；μs為靜摩擦因數；μm為動摩擦因數，μs≥μmN表示摩擦表面之間的正壓力；vm為最小動摩擦因數對應的滑動速度，并且滿足|μ(0)| ≤μs，|μ(vm)|=μm，μ′(vm)=0，μ(-vr)=-μ(vr)，μ′(-vr)=μ′(vr)，

滑塊在移動帶上靜止時的相對速度vr的數值為0，當滑塊在帶上開始滑動時，摩擦力數值最初減小，而后隨著速度的增加而增加。

2 系統的穩定性和黏滑運動特性理論分析

設ω0=可以獲得式（3）所示的無量綱變量和參數

將式（3）代入式（1），求得系統運動微分方程的無量綱表達式為

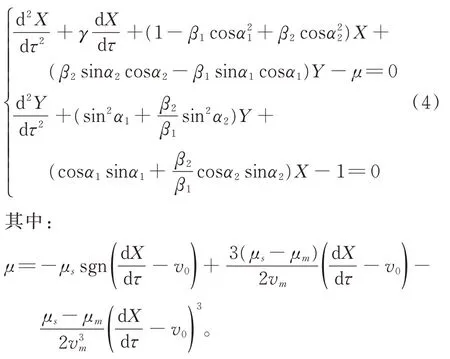
根據常微分方程理論，任何正規高階微分方程都可以轉化為等價的1 階微分方程組。故對系統的微分方程進行等價變換，可以令

把式（5）代入式（4），可以得到如式（6）所示的1階微分方程組

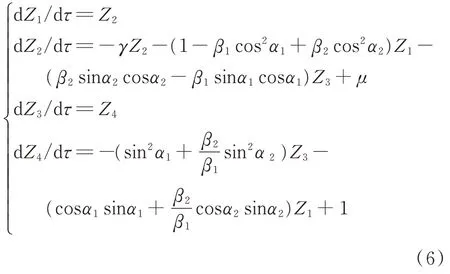
當系統輸入速度足夠大時，在摩擦力和彈簧力的作用下，滑塊處于靜平衡狀態。在這種平衡狀態下，系統初始條件設為：并且符號函數sgn(vr)=-1。系統參數值設置如下：μs=0.8，μm=0.6，vm=0.45 m/s。利用李雅普諾夫穩定性理論分析了系統平衡點的穩定性。當時，由式（6）可求得系統的平衡點為

將式（6）右端展開成泰勒級數，并略去二次以上的項，可以得到系統的1 階近似微分方程的雅可比矩陣為

系統的無量綱參數設置如下：β1=β2=0.001，γ=0.02，α1=將上述參數代入式（8）可得矩陣A的特征方程為

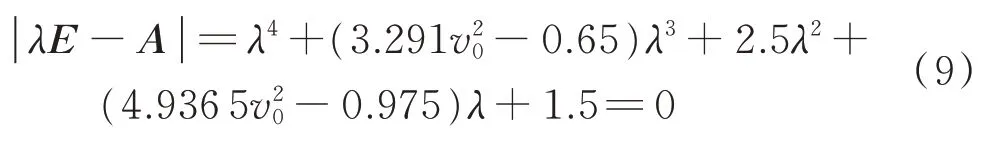
使用文獻［12］中的計算公式可以獲得系統的臨界黏滑速度為

其中：Fs-Fm為靜摩擦力和動摩擦力的差值；c1+c2為系統的阻尼；k為系統的等效剛度；m為滑塊的質量。

本研究中各參數為：Fs-Fm=0.2，c1+c2=0.02，k=1，m=1。將以上各參數數值帶入式（10）可求得系統的臨界黏滑速度為0.564 3m/s。理論分析表明，當系統驅動速度低于該臨界值時，滑塊在運行過程中會出現黏滑運動現象；當系統驅動速度高于該臨界值時，滑塊在運行過程中不會出現黏滑運動現象。

為了對理論計算結果進行驗證，筆者采用數值計算的方法求解了式（4）給出的焦爐推焦系統的運動方程，分析了不同驅動速度下系統的穩定性和黏滑運動特性。推焦系統仿真參數設置如下：β1=β2=0.001，γ=0.02，α1=π/3，α2=2π/3，M=1，Kx=1，Ky=1.5。在推焦系統中推焦裝置材料為Q235 鋼，炭化室地面為耐火磚，實際工作中炭化室內溫度在1 000℃左右。推焦裝置和耐火磚之間通過紅焦接觸，其表面情況非常復雜，根據企業工程實際經驗，動靜摩擦因數分別設定為［13］μs=0.8，μm=0.6。系統初始條件滿足X=0，。系統驅動速度分別設置為：0.35，0.42，0.5，0.54，0.6，0.65 m/s。對系統進行仿真，獲得的相圖如圖3所示。

圖3 不同驅動速度下的系統相圖Fig.3 The phase diagrams with different excitation speeds

由圖3 可知，驅動速度不同時，系統響應的數值計算結果也不同。從圖3（a，b）中可以看出，當系統驅動速度低于系統臨界失穩速度v0=vb0=0.444 4 m/s 時，系統處于不穩定狀態，而且存在明顯的黏滑運動現象；從圖3（c，d）中可以發現，當系統驅動速度高于系統臨界失穩速度而低于系統的臨界黏滑速度0.564 3m/s 時，系統穩定在平衡點，黏滑運動依然很明顯；圖3（e，f）的相圖表明，當系統驅動速度高于系統臨界失穩速度和臨界黏滑速度時，系統穩定在平衡點，同時不會出現黏滑運動現象。

通過推焦作業現場實際測試，發現推焦過程中推焦裝置的平均工作速度一般為0.25～0.45m/s，該值低于系統的臨界失穩速度和臨界黏滑速度，表明推焦作業過程中容易發生黏滑振動現象。根據企業工程技術人員的現場經驗，認為動靜摩擦因數的差值可能對推焦裝置的穩定性和黏滑振動有重要的影響，因此筆者采用數值仿真的方法詳細分析了動靜摩擦因數差值的變化對推焦裝置穩定性和黏滑特性的影響。

為了更全面地分析問題，筆者將摩擦因數的變化分成了兩種情況進行討論：①在不改變靜摩擦因數的前提下，通過增大動摩擦因數的方法來減小動靜摩擦因數的差值；②在不改變動摩擦因數的前提下，通過減小靜摩擦因數的方法來減小動靜摩擦因數的差值。

3 動靜摩擦因數變化對焦爐推焦系統穩定性的影響

3.1 靜摩擦因數不變而動摩擦因數增大

仿真系統參數設置為：β1=β2=0.001，γ=0.02，α1=π/3，α2=2π/3，v0=0.4 m/s，M=1，Kx=1，Ky=1.5，μs=0.8。系統滿足如下初始條件：X=0，=0，Y=0，=0。系統的靜摩擦因數減去動摩擦因數的差值分別取為：0.2，0.1，0.05，0.02，0.01，0.001。對系統進行仿真，獲得的相圖如圖4 所示，獲得的Poincare 截面圖如圖5 所示。從圖4 中可以看出，隨著動靜摩擦因數差值的不斷減小，極限環外部的相軌跡逐漸卷向極限環，而且極限環不斷地縮小，表明系統由不穩定狀態逐漸轉為穩定狀態。由圖5 中的Poincare 截面圖可知，在不同動靜摩擦因數差值的情況下，系統都能夠進行準周期運動。

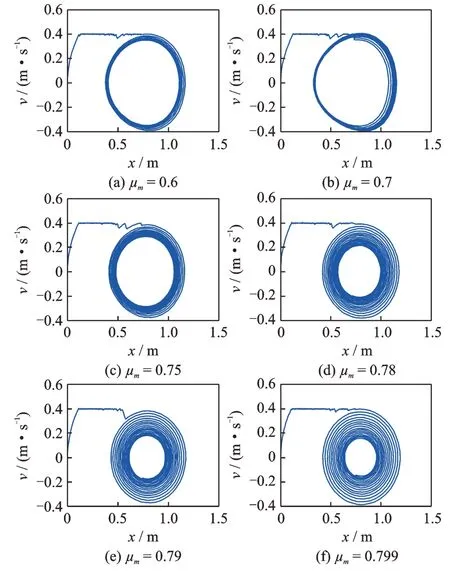
圖4 靜摩擦因數不變而動摩擦因數增大工況下的相圖Fig.4 The phase diagrams with the condition of constant static friction factor and increasing dynamic friction factor

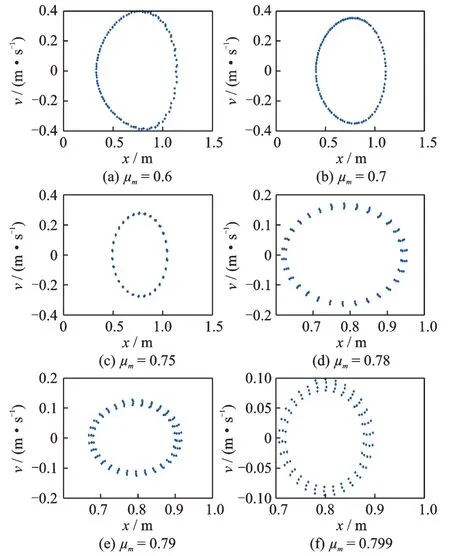
圖5 靜摩擦因數不變而動摩擦因數增大工況下的的Poin‐care 截面圖Fig.5 The Poincare sectional views with the condition of constant static friction factor and increasing dynamic friction factor

3.2 動摩擦因數不變而靜摩擦因數減小

仿真系統參數設置為：β1=β2=0.001，γ=0.02，α1=π/3，α2=2π/3，v0=0.4 m/s，M=1，Kx=1，Ky=1.5，μm=0.6。系統滿足如下初始條件：X=0，=0，Y=0，=0。系統的靜摩擦因數減去動摩擦因數的差值分別取為：0.2，0.1，0.05，0.02，0.01，0.001。對系統進行仿真，獲得的相圖如圖6 所示，獲得的Poincare 截面圖如圖7 所示。由圖6 可以看出，隨著動靜摩擦因數差值的逐漸減小，極限環外部的相軌跡逐漸卷向極限環，而且極限環不斷地縮小，表明系統由不穩定狀態逐漸轉為穩定狀態。由圖7 中的Poincare 截面圖可知，在不同的動靜摩擦因數差值情況下，系統都能夠進行準周期運動。

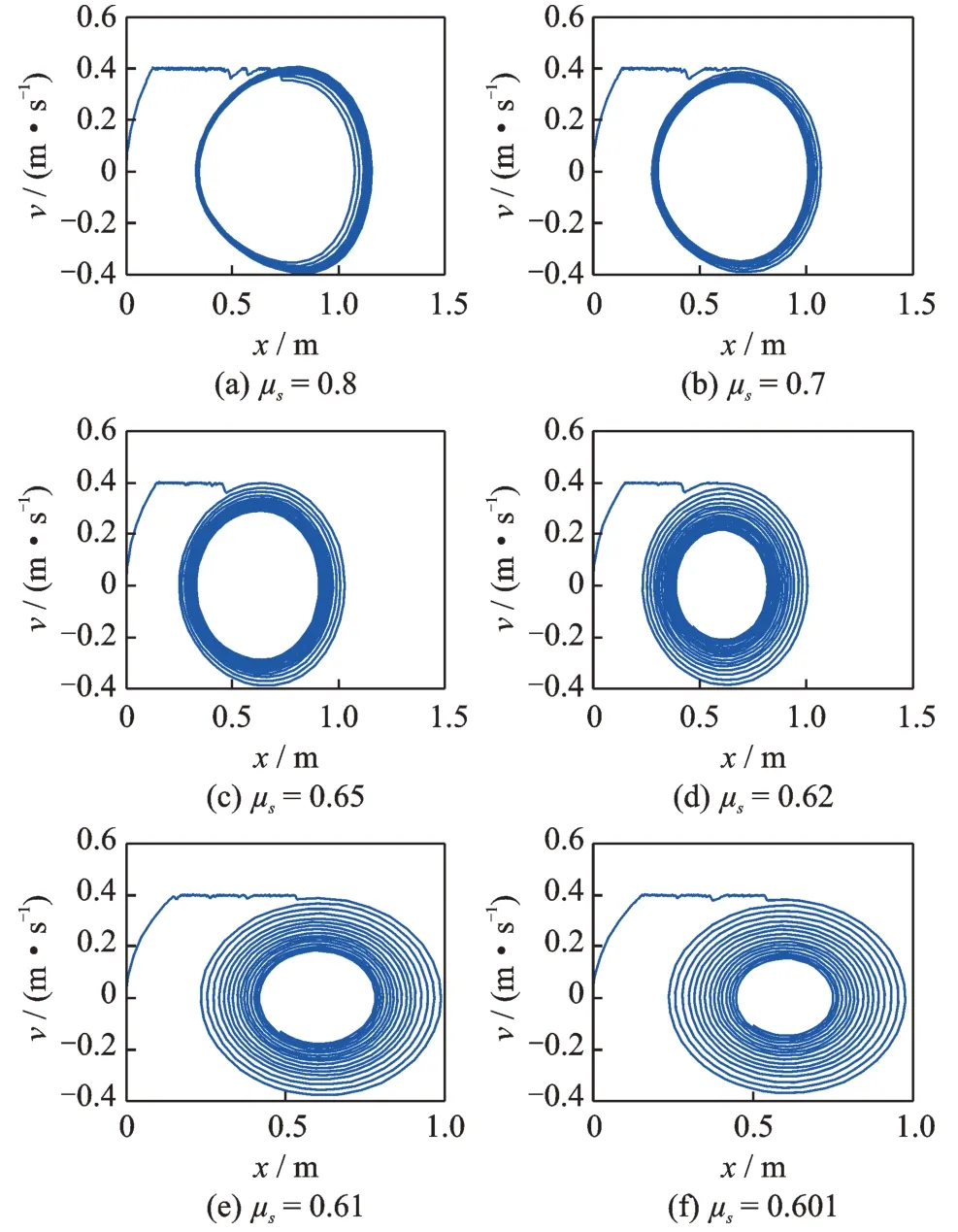
圖6 動摩擦因數不變而靜摩擦因數減小工況下的相圖Fig.6 The phase diagrams with the condition of constant dy‐namic friction factor and decreasing static friction factor

圖7 動摩擦因數不變而靜摩擦因數減小工況下的Poincare截面圖Fig.7 The Poincare sectional views with the condition of constant dynamic friction factor and decreasing static friction factor

4 動靜摩擦因數變化對焦爐推焦系統黏滑運動特性的影響

由圖4 和圖6 的相圖分析結果可知，在改變動靜摩擦因數差值的情況下，系統的黏滑運動現象一直存在。為了定量表征動靜摩擦因數變化對焦爐推焦系統黏滑運動特性的影響，本節采用多體動力學仿真的方法對其進行了研究。

4.1 靜摩擦因數不變而動摩擦因數增大

推焦系統仿真參數設置為：m=4.12×104kg，v0=0.5 m/s，k1=7.433×103N/m，k2=7.433×103N/m，k3=7.433×106N/m，c=3.5×102（N?s）/m，μs=0.8。滑履與炭化室地面間靜摩擦因數減去動摩擦因數的差值分別取為：0.3，0.25，0.2，0.15，0.1，0.05。采用ADAMS 仿真軟件對推焦裝置進行動力學仿真獲得的推焦裝置速度響應曲線如圖8 所示。從圖8 中可以明顯地看出，隨著動靜摩擦因數差值的減小，推焦裝置的黏滑運動現象越來越嚴重，從最初的只發生在前4s 的時間，到最后在整個10s 時間內均發生了黏滑運動。

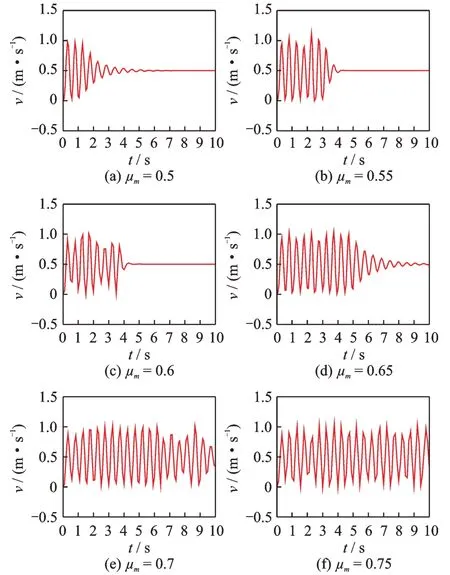
圖8 靜摩擦因數不變而動摩擦因數增大工況下的速度響應曲線Fig.8 The velocity response curves with the condition of con‐stant static friction factor and increasing dynamic fric‐tion factor

4.2 動摩擦因數不變而靜摩擦因數減小

推焦系統仿真參數設置為：m=4.12×104kg，v0=0.5 m/s，k1=7.433×103N/m，k2=7.433×103N/m，k3=7.433×106N/m，c=3.5×102（N?s）/m，μm=0.6。滑履與炭化室地面間的靜摩擦因數減去動摩擦因數的差值分別取為：0.3，0.25，0.2，0.15，0.1，0.05。采用ADAMS 仿真軟件對推焦裝置進行動力學仿真獲得的推焦裝置速度響應曲線如圖9 所示。由圖9 可知，在動靜摩擦因數差值較大的情況下，推焦裝置發生黏滑振動現象的時間比較短；在動靜摩擦因數差值不斷減小的情況下，推焦裝置的黏滑運動現象逐漸增多。

圖9 動摩擦因數不變而靜摩擦因數減小工況下的速度響應曲線Fig.9 The velocity response curves with the condition of con‐stant dynamic friction factor and decreasing static fric‐tion factor

5 結論

1）利用李雅普諾夫穩定性理論分析了系統的穩定性，計算求得系統的臨界失穩速度為0.444 4 m/s。通過理論公式計算了系統的臨界黏滑速度，其值為0.564 3m/s。當系統驅動速度小于0.444 4 m/s 時，系統將發生失穩。當系統驅動速度小于0.564 3 m/s 時，系統會發生黏滑運動。

2）動靜摩擦因數的差值對系統的穩定性有很大的影響，無論通過增大動摩擦因數還是減小靜摩擦因數使得動靜摩擦因數差值減小，都能促進系統趨近穩定狀態。

3）動靜摩擦因數的差值對系統的黏滑運動也有一定的影響，減小動靜摩擦因數的差值并不能減輕系統的黏滑運動現象，反而有可能使系統振動加劇。

4）為了提高推焦系統的穩定性，可以通過提高裝置的制造和安裝精度來提高推焦桿下表面的平面度，使推焦桿的下表面盡可能平行于炭化室地面；也可以采用耐磨和耐熱性好、強度高的材料作為滑履底部材料，以減小滑履和炭化室地面的摩擦。為了減輕推焦系統的黏滑運動，可在推焦裝置投產前及維護階段對炭化室地面的耐火磚進行打磨，盡可能使炭化室地面保持平整；改進滑履結構使其可以根據炭化室地面的工況，自動調整滑履底面和炭化室耐火磚的接觸面來減小摩擦。