一種自標定的港口起重機械攝影測量方法

李和平，王 源，趙章焰，魯恩順

(武漢理工大學物流工程學院，湖北 武漢 430063)

1 引言

港口起重機械作為一種工作環境惡劣的大型工程機械，其安全狀態評估一直受到人們的關注[1]。港口起重機械在工作過程中大梁、立柱等關鍵部位的變形一直是安全評估的重點[2]。目前能夠測量港口起重機械關鍵部位形變的方法主要有：布設傳感器[3]、全站儀測量[4]、激光掃描。其中，布設傳感器是目前最常用的方法，但該方法需要人工操作，工作量大，測量過程中操作人員的人身安全得不到保障；全站儀測量和激光掃描完成一次對港口起重機械整機的測量所需的時間周期長，成本高。

隨著拍攝技術的進步，基于普通數碼相機的近景攝影測量技術在工程測量領域的應用更加廣泛[5-6]。而將攝影測量技術應用到港口起重機械的測量領域面臨著兩個重大的問題：(1)港口起重機械體型較大，而普通數碼相機視場角較小，受限于設站位置，往往只能拍攝到港口起重機械的一部分結構，需要多次設站拍照；(2)現有攝影測量算法必須在港口起重機械周圍布設一定數量的控制點[7]，從而確定拍攝時像片的外方位元素Xs，Ys，Zs，φ，ω，κ，其中Xs，Ys，Zs為相機攝影中心在物方空間坐標系的三維坐標，φ，ω，κ是攝影光束的轉角[7]。

為了解決以上問題，提出基于系統自標定的旋轉攝影測量方法。將相機和旋轉平臺連接，旋轉平臺可以實現繞豎直方向旋轉和水平方向的俯仰，單次設站即對港口起重機械整機拍攝；旋轉平臺下布置水平滑軌，無需移動整個平臺，即可在兩個不同的位置完成對待測物體的拍攝；在港口進行拍攝之前借助已知模型確定相機的回轉參數，在實驗中記錄相機旋轉的角度，實時求解相機在空間中的位置和姿態，實現系統的自標定，無需在港口起重機械上設置控制點。

2 系統自標定

2.1 相機坐標系的旋轉變換

相機坐標變換示意圖，如圖1所示。坐標系O-XYZ為物方空間坐標系，即世界坐標系。坐標系A-XAYAZA為旋轉平臺的機器坐標系，YA軸和ZA軸為初始狀態下旋轉平臺的兩個旋轉軸。坐標系S-XsYsZs是以相機投影中心為原點建立的坐標系。

旋轉平臺下連接有水平滑軌，相機旋轉過程水平滑軌保持靜止，初始狀態下旋轉平臺YA軸的指向和滑軌的方向相同，原點A為兩個旋轉軸的交點。相機在旋轉平臺上的安裝示意圖，如圖2所示。ZA軸為豎直方向，YA軸為水平方向。相機繞YA軸俯仰，繞ZA軸周向旋轉，當相機繞YA軸旋轉時，旋轉平臺ZA軸保持靜止；當相機繞ZA軸旋轉時，旋轉平臺YA軸也隨之旋轉。

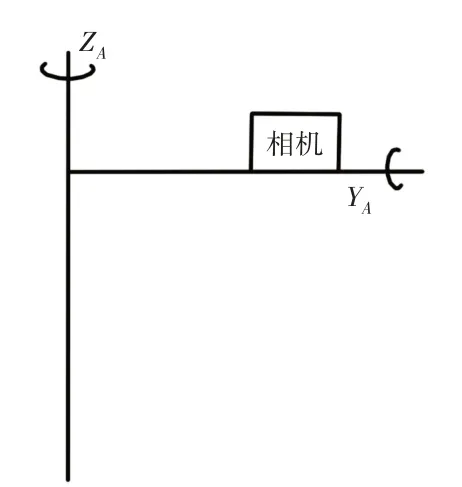
圖2 相機安裝示意圖Fig.2 Camera Installation Diagram

2.2 確定回轉參數

正式拍攝之前需在實驗室內進行系統的自標定，確定相機的回轉參數。先在初始狀態拍攝標定模型，記錄相機初始狀態；繞ZA軸旋轉拍攝標定模型，取三張照片，回歸初始狀態；然后繞YA軸旋轉拍攝標定模型，取三張照片，回歸初始狀態。標定模型上設置四個已知點，根據共線條件方程[8]，式(1)，式(2)，進行后方交會[9]可以解算出每張像片的外方位元素，即拍攝時相機在物方空間坐標系中的位置和姿態。

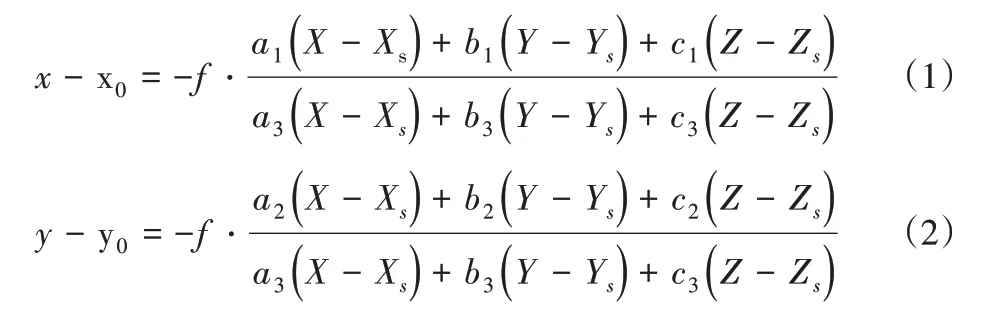
式中：x，y，-f—像點在像空間坐標系中的坐標，x0，y0—像主點的坐標，f—相機的焦距；(Xs，Ys，Zs)—攝影中心在物方空間坐標中的坐標，(X，Y，Z)—測量點在物方空間坐標中的坐標，ai，bi，ci—像片三個外方位角組成的九個方向余弦[9]。

根據上述公式，可以得到相機在繞單個軸旋轉過程中投影中心的三個位置在物方空間坐標系的三維坐標(x1，y1，z1)，(x2，y2，z2)，(x3，y3，z3)，以及初始狀態時在空間中位置S(xs，ys，zs)。三個點的坐標可確定一個圓，圓心O(x0，y0，z0)為相機旋轉中心，圓的半徑R是相機的旋轉半徑，如式(3)所示：

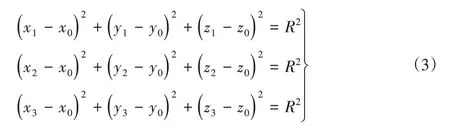
三個空間點可確定一個平面，平面方程如式(4)：

根據平面的方程，可求得該平面的法向量f=(x1，y1，z1)，即為旋轉軸指向的方向。

根據上述公式，可求得初始狀態下相機繞ZA軸回轉的法向量fz=(xz，yz，zz)，為旋轉軸ZA指向的方向，旋轉中心Oz(xz，yz，zz)，旋轉半徑Rz；繞YA軸回轉的法向量fy=(xy，yy，zy)，為旋轉軸YA指向的方向，旋轉中心Oy(xy，yy，zy)，旋轉半徑Ry。根據兩個法向量可求出旋轉軸XA指向的方向fx=(xx，yx，zx)。

由于相機的安裝和制造誤差，相機不可能完全對心安裝。在相機繞ZA軸旋轉所確定的平面上，相機初始位置S和旋轉中心Oz所組成的向量OzS的長度為旋轉半徑Rz，在fx和fy方向的投影分別為Ly，Lx：

同理，可求得相機繞YA軸旋轉所確定的平面上，相機初始位置S和旋轉中心Oy所組成的向量OyS的長度為旋轉半徑Ry，在fz方向的投影為Lz：

實驗室自標定完成后，即可確定初始狀態下相機投影中心和旋轉平臺的相對位置關系，以及相機旋轉過程中的旋轉參數。實際拍攝時，相機固定在初始位置。相機的旋轉半徑Ry、Rz，以及初始位置的投影Lx、Ly、Lz保持不變。

3 旋轉測量方法

3.1 拍攝步驟

在實驗室完成相機自標定后進行實際測量。保證相機固定在旋轉平臺上的初始位置，記錄此時旋轉平臺的兩個旋轉軸ZA和YA的初始角度αLz和αLy，先繞YA軸進行旋轉，記錄此時角度βLy，再繞ZA軸旋轉，直至相機對準待測物體，記錄此時角度βLz，拍攝照片，此時的照片命名為左片。然后回歸初始狀態，保持相機和回轉中心相對固定，將相機和旋轉平臺整體沿水平滑軌移動一定的距離，重復上述過程直至相機對準待測物體，此時照片命名為右片。運用旋轉矩陣解算出左片、右片兩張像片的外方位元素[10]，雙片前方交會即可確定待測點的坐標。

3.2 求解外方位元素

在機器坐標系A-XAYAZA中，相機初始位置為S0(xs，ys，zs)。以S0為原點，分別以fx，fy，fz方向作為X，Y，Z三條坐標軸的方向建立三維坐標系S-XsYsZs。

坐標系S-XsYsZs和坐標系A-XAYAZA存在如下關系：

相機在坐標系A-XAYAZA中繞YA軸和ZA軸旋轉，因YA軸會隨ZA軸旋轉，故先計算繞YA軸的旋轉。旋轉過程中角度的變化量下：

設相機繞YA軸旋轉之后在坐標系A-XAYAZA的坐標為S1(x1，y1，z1)。點S0和S1滿足關系式(11)。

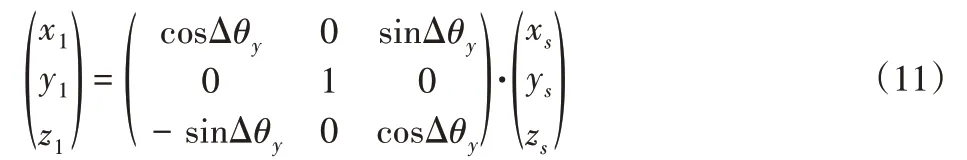
設相機拍攝左方照片時的坐標為S2(x2，y2，z2)，則有：

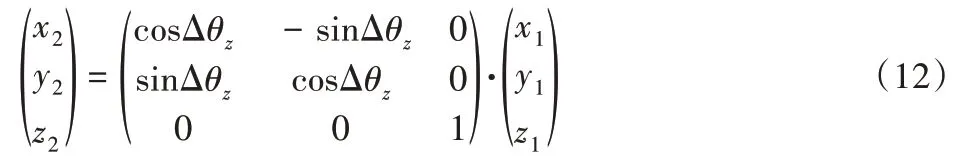
解算出左方像片拍攝時的三維坐標之后，根據式3-1換算到坐標系S-XsYsZs中，由于相機旋轉角已知，則在坐標系S-XsYsZs中左方像片所有的外方位元素都已求解出。

左方像片拍攝完成后將旋轉平臺和相機恢復初始狀態，沿水平滑軌移動到右方像片拍攝位置，解算出右方像片拍攝時相機投影中心的三維坐標S3(x3，y3，z3)，將S3的坐標換算到左方照片拍攝時的坐標系S-XsYsZs中，則在坐標系S-XsYsZs中右方照片所有的外方位元素都已求解出。該方法無需在被測物體上布置控制點，實現了系統的自標定，解決了在港口起重機械上無法布置控制點的問題。同時，由于相機可以在平臺上平移和旋轉來拍攝，避免了相機視場角的問題。

4 實驗分析

4.1 標定相機

試驗所選擇的相機型號為佳能EOS 5DS，分辨率8688×5792，搭配的鏡頭型號為EF 50mm f/1.8 STM。

試驗所采用的相機標定方法是MATLAB提供的Camera Calibrator工具箱。標定過程，如圖3所示。

圖3 相機標定過程Fig.3 Camera Calibration Process

經過計算，得到相機的標定參數，如表1所示。

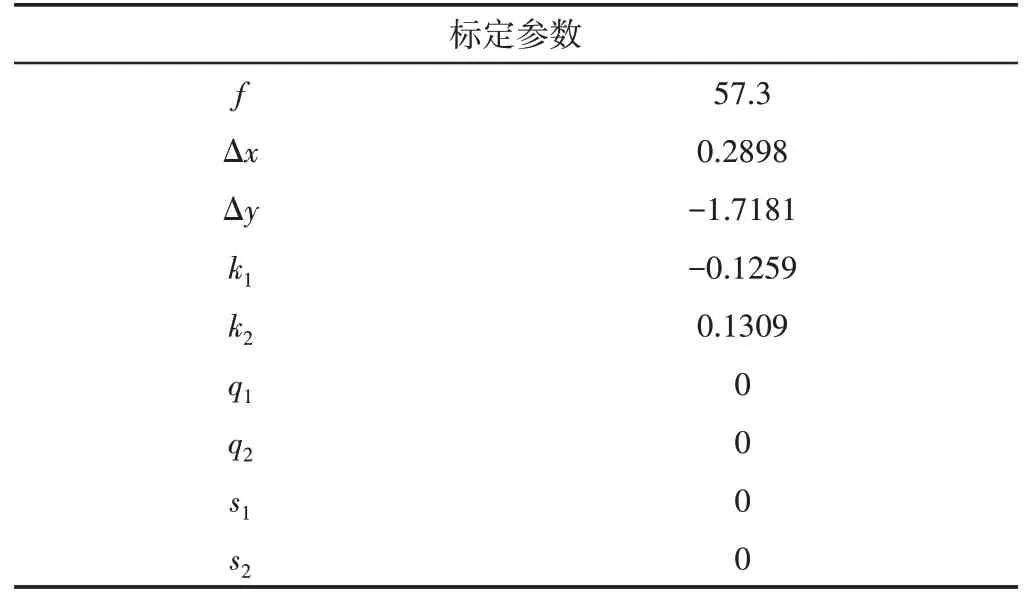
表1 相機標定參數Tab.1 Results of the Calibration

4.2 試驗過程

實驗流程，如圖4所示。

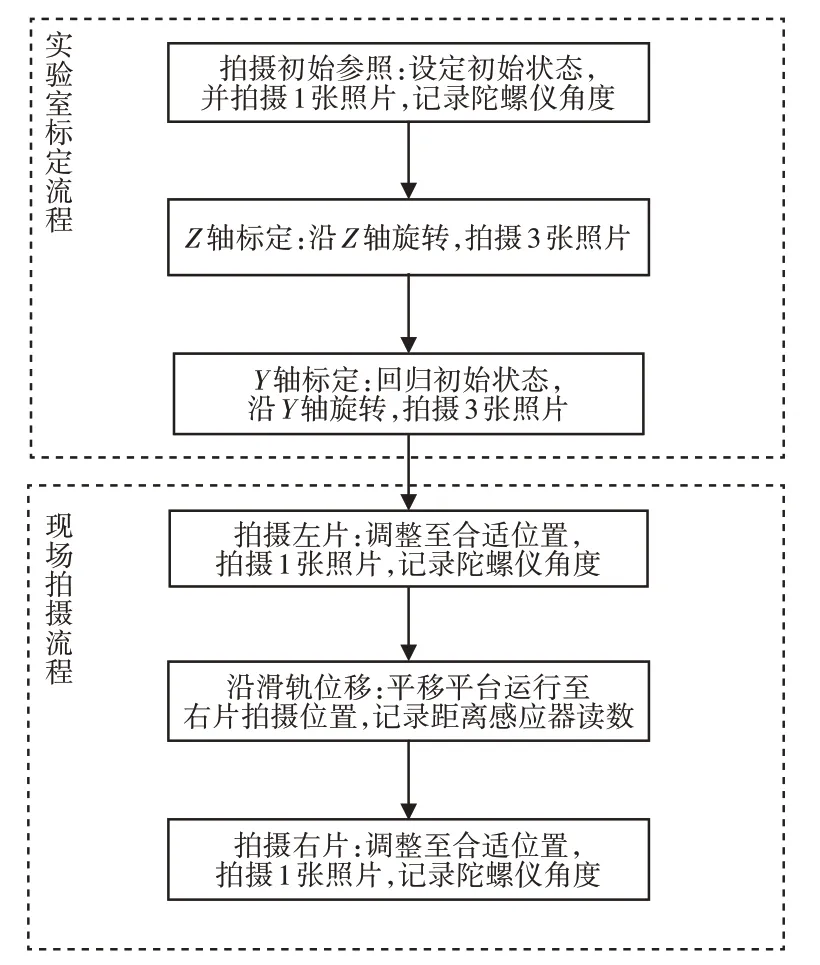
圖4 實驗流程Fig.4 Experiment Process

自標定所用模型，如圖5所示。本次實驗采用的模型為黑、白兩色的立方體，黑色立方體邊長為100mm，白色立方體邊長為50mm，圖中點1、點2、點3、點4為自標定過程中的4個控制點。

圖5 自標定模型Fig.5 Self-Calibration Model

自標定完成后保持相機、旋轉平臺和水平滑軌的相對位置不變，移動整體以拍攝待測物體。拍攝狀態，如圖6所示。實驗設備，如圖7所示。

圖6 相機拍攝狀態Fig.6 Camera Shooting Process

圖7 實驗設備Fig.7 Experimental Equipment for Camera Shooting

為計算方便，取主梁上筋板的間距作為計算精度的評價指標，待測點分布，如圖8所示。

圖8 待測點分布Fig.8 Distribution of Points to be Measured

4.3 實驗結果

拍攝像片的外方位元素，如表2所示。前方交會求得待測點的坐標，如表3所示。各個待測點之間的相對距離分析，如表4所示。

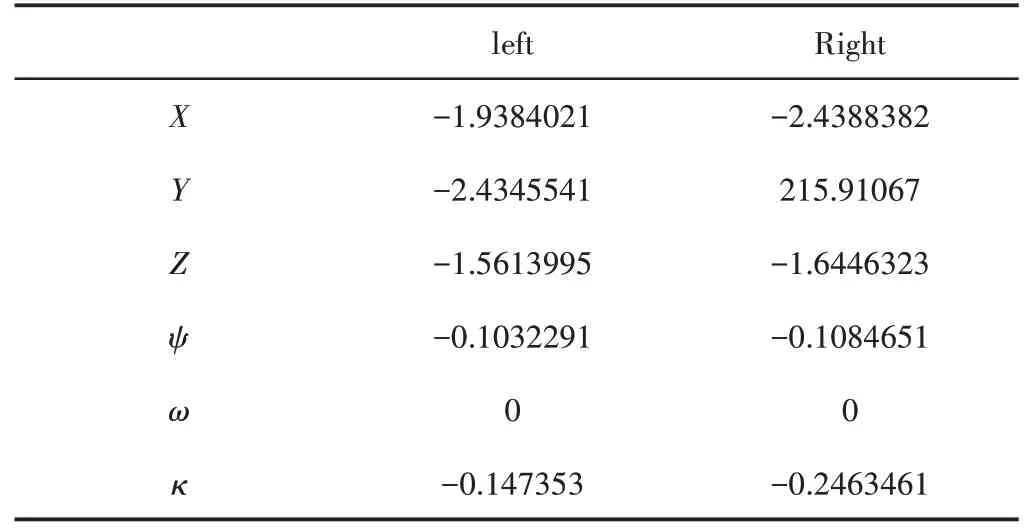
表2 像片的外方位元素Tab.2 Outer Orientation Element

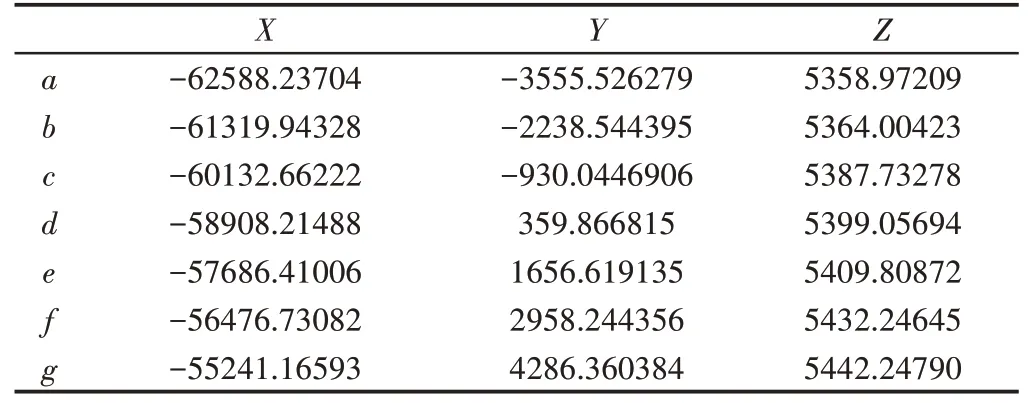
表3 待測點坐標Tab.3 Point Coordinates to be Measured

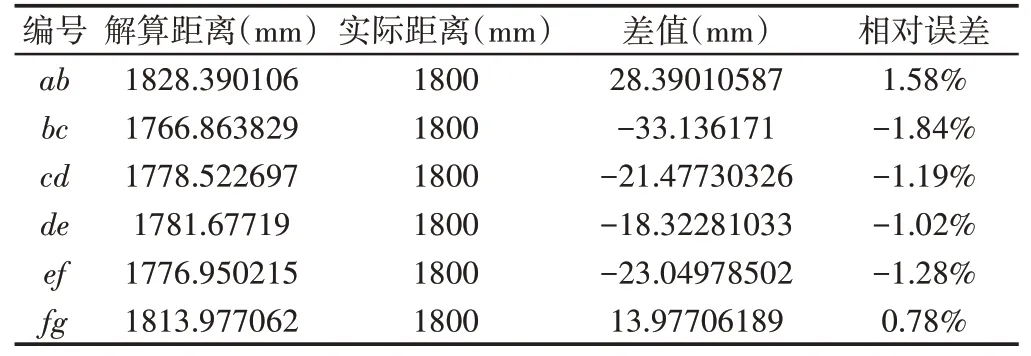
表4 待測點之間的相對距離Tab.4 Relative Distance Between Points to be Measured

5 結論

(1)實驗表明，提出的自標定方法無需現場布設控制點，實現了在遠距離精確測量港口起重機械的結構尺寸，能夠滿足港口環境的應用需求。(2)解算出的待測點相對距離誤差最大值為1.84%，最小值為0.78%，滿足港口起重機械安全評估中對于主要結構件外形尺寸的誤差要求。并且，也可用于建筑測繪，大型工程機械外形尺寸測量等拍攝條件苛刻，精度要求較高的場合。(3)目前，所提出的方法仍存在著提升空間，由于不同像片的同名點匹配主要依賴于人工選擇，其精度的穩定性及自動化程度均有待提高。未來通過引入機器學習的方法，同名點的匹配將能夠通過計算機自動完成，這一方法的執行效率及測量結果的精度將得以進一步的提升。