飽和軟黏土中梯形淺基礎承載特性研究
于 洋,張 偉,劉孟孟,李越松
(1.天津大學 建筑工程學院,天津 300350;2. 交通運輸部天津水運工程科學研究所 港口水工建筑技術國家工程實驗室 水工構造物檢測、診斷與加固技術交通行業重點實驗室,天津 300456)
張偉等[3-4]對挪威國家石油公司1994年和1995年安裝的兩座筒型基礎平臺的計算理論進行分析并指出其優缺點,并假設筒型基礎土體的水平抵抗力服從Winkler假定,按空間問題處理推導出更具一般性的筒型基礎水平極限承載力顯式計算公式,采用大港灘海試驗場地土質條件進行模型試驗,理論推導與試驗結果吻合性良好。孫大鵬等[5]研究了不同直徑和高度的單桶基礎和四桶基礎在豎向荷載和水平荷載單獨作用下的地基破壞模式,并給出了承載力計算的近似方法。劉振紋等[6]進行了單桶模型試驗以及單桶和雙桶對比模型試驗,明確了土體主動區與被動區的土壓力分布,結合有限元數值計算并參考極限平衡法Engel假定給出了單桶基礎水平承載力計算公式,通過定義多桶效率系數研究了桶間距對地基水平承載力影響。李向東等[7]通過模型試驗,確定了軟黏土地基中筒型基礎的水平和豎向極限承載力,建議使用斯凱普頓公式計算飽和軟黏土中筒型基礎的豎向承載力,使用劉振紋等[6]提出的公式計算飽和軟黏土中筒型基礎水平承載力。馬鵬程等[8]基于大比尺模型試驗,發現筒內只有部分土體與基礎具有協同作用,進一步提出筒土協同度的概念,并運用數值模擬方法分析加荷條件、筒型基礎結構尺寸、筒內分倉形式、分倉板高度和厚度以及筒土相對剛度等因素對筒土協同度的影響。天津大學海上風電課題組丁紅巖等[9-10]結合我國近海地質條件和風機基礎荷載特點,創新性地提出了由弧線型過渡段和基礎筒組合而成的寬淺式筒型基礎這一新型海上風機基礎形式,從傳統小直徑筒型基礎以筒壁摩阻力為主的受力模式轉化為以筒頂承載力為主的受力模式,大幅度提高了筒型基礎的可靠性和穩定性。此外,方許聞等[11]針對不同形式的樁基礎影響下的二維流場、劉文白[12]針對新型樁-桶基礎的上拔特性均采用數值計算的方法進行了仿真與研究。
裙板的存在使傳統筒型基礎水平抗力增大、抗滑力提高,但基礎安裝過程需要借助真空泵,安裝時間長、安裝效率低、安裝成本隨水深增加而急劇上升。為降低成本和安裝難度,本文提出了混凝土梯形淺基礎結構,采用數值模擬的方法研究了水平、豎向和彎矩荷載單獨作用下的地基承載特性,進行歸一化處理后得出了極限承載力系數計算公式。
1 淺基礎結構形式及模型驗證
1.1 淺基礎結構二維模型
為詳細探究梯形淺基礎的承載特性,采用大型有限元分析軟件ABAQUS建立了梯形淺基礎的二維數值模型,淺基礎詳細尺寸見表1,模型示意圖見圖1。通過改變數值模型中梯形淺基礎的深寬比d/B(埋深與上底寬度之比)和傾斜角度α(梯形斜邊與豎直方向的夾角)以探究不同方向的荷載單獨作用下不同尺寸基礎的極限承載力。
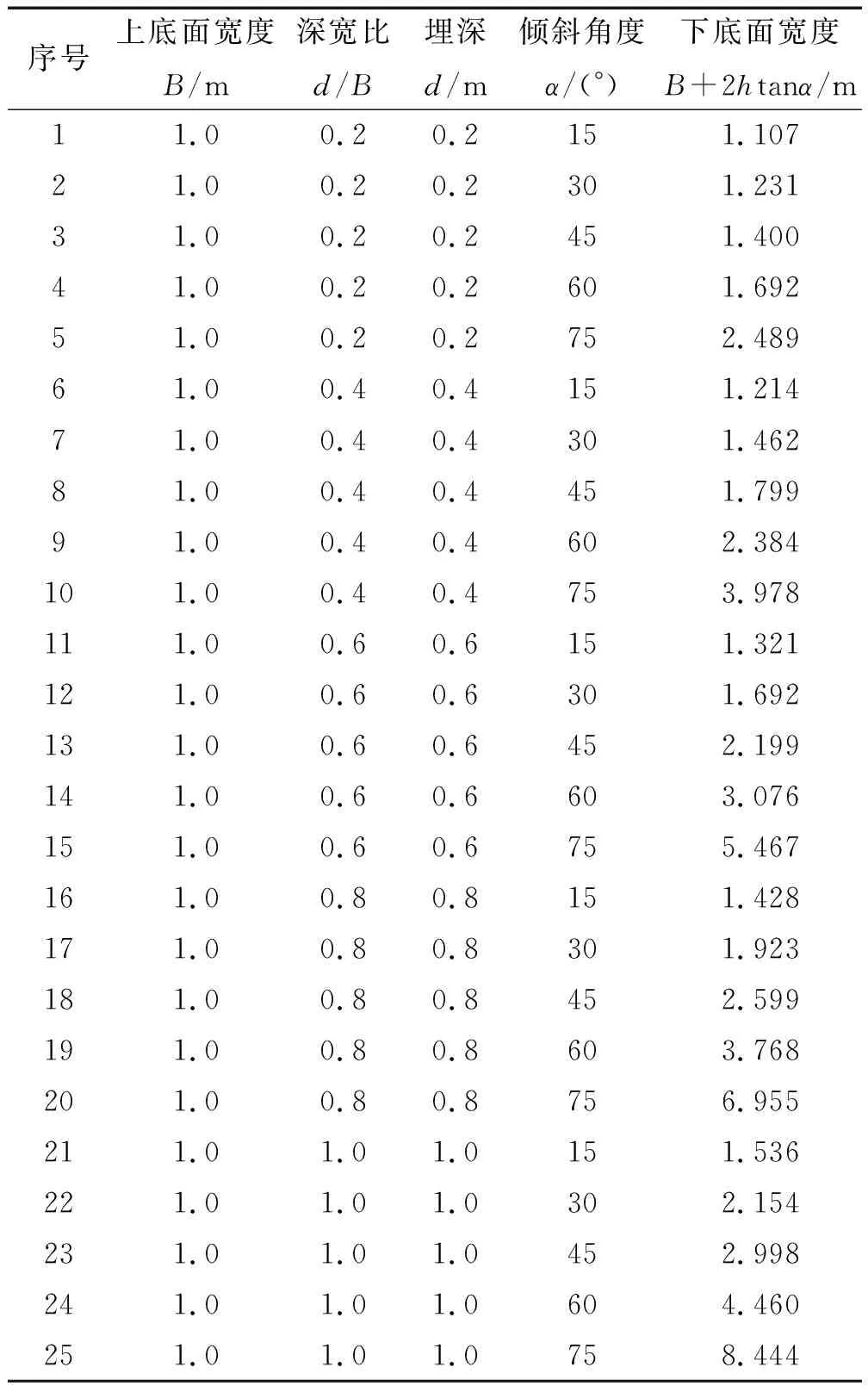
表1 基礎尺寸對照Tab.1 Basic size comparison
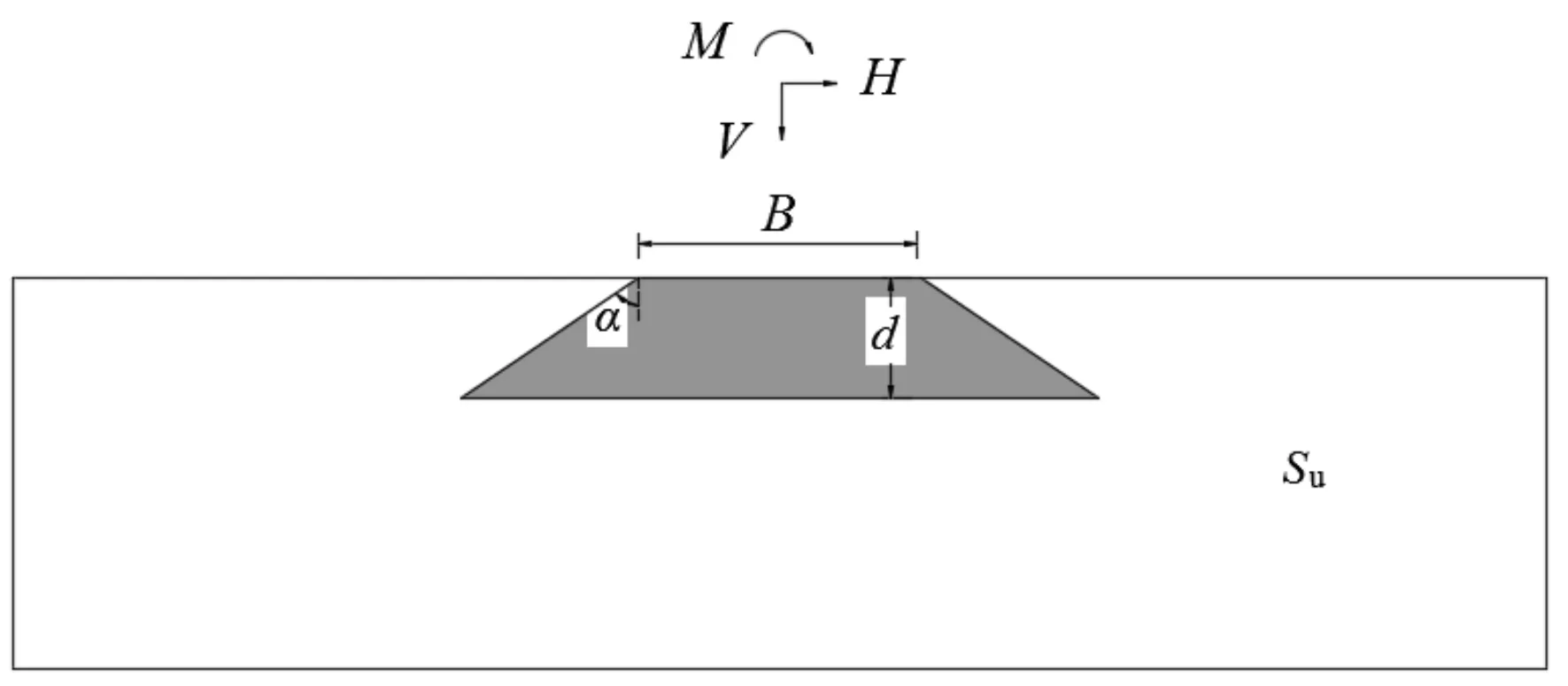
圖1 梯形淺基礎二維有限元模型示意圖Fig.1 Schematic diagram of two-dimensional finite element model of trapezoidal shallow foundation
有限元模型中,梯形淺基礎材質為混凝土,采用基于理想彈塑性本構模型的材料模擬,其密度ρ=2 560 kg/m3,彈性模量E=30 GPa,泊松比v=0.2;海床土體為不排水飽和軟黏土,采用基于Tresca屈服準則的理想彈塑性本構模型模擬,其密度ρ=600 kg/m3,彈性模量E=3.351 MPa,泊松比v=0.48,不排水剪切強度Su=3 400 Pa,暫不考慮不排水強度梯度,內摩擦角和剪脹角均為0。考慮到混凝土基礎的彈性模量大于土體的彈性模量,指定主控接觸面位于基礎上而從屬接觸面位于土體上,由于基礎和深海土體接觸面之間的張力效應,且考慮到極限承載力狀態下基礎的位移和轉角相對較小,基礎側面和底面與土體緊密結合、尚未分離,故有限元模型中接觸表面切向行為設置為完全粗糙,法向行為設置為硬接觸,且基礎與土體接觸后不允許分離。基礎和土體的網格選用C3D8R單元類型。在不影響計算精度的情況下為提高運算效率,土體的網格劃分采用單精度偏移的方式,網格尺寸從基礎向四周均勻增加,即與基礎接觸的土體網格尺寸最小,為0.05 m,土體邊界的網格尺寸最大,為0.5 m;基礎的網格均勻劃分,精度與土體的最小尺寸保持一致。土體側面邊界限制水平位移,底面邊界限制水平位移、豎直位移和轉角。
數值模型中梯形淺基礎的荷載作用點LRP位于坐標軸原點,即基礎頂面形心處。施加單項荷載之前通過地應力平衡消除自重影響。針對荷載作用點分別單獨作用水平荷載H、豎向荷載V和彎矩荷載M,基礎相應地發生水平位移h、豎向位移v和轉角θ。荷載作用方向和位移轉角符號的規定遵從Butterfield的建議。
1.2 模型驗證
為驗證數值模型的正確性,考慮傾斜角度α=0時的情況,此時梯形淺基礎退化為矩形淺基礎,建立與梯形淺基礎上底寬度和高度相同(即寬度B=1 m,高度d=0.2 m)的無埋深矩形淺基礎二維有限元模型,其余參數和設置均與梯形淺基礎保持一致,將有限元數值計算結果與地基規范中Prandtal和Reissner提出的極限承載力公式比較,對比極限承載力系數。
實行變化管理的有效控制就是要從變化的出現到變化的完成實現全方位的閉合管理,使整個變化過程都在掌控之中。天脊集團對變化信息確定了預測、匯報、處理、檢查、落實、完成六個程序,確保高效運行。
經過計算可知,數值模型計算得到的豎向承載力系數Nc=5.19,與Prandtal和Reissner的經典理論解的Nc=5.14相比,誤差為0.97%;數值模型計算得到的水平承載力系數Nh=1.01,與Prandtal和Reissner的經典理論解的Nh=1相比,誤差為1%;由此可知,數值計算中選取的模型參數和網格劃分方法等具有較高的準確性和可信度。
2 淺基礎單項承載力
2.1 豎向極限承載力Vult
在ABAQUS中分別建立表1中的梯形淺基礎有限元模型,采用位移控制法進行加載計算,得到不同尺寸梯形淺基礎的豎向極限承載力Vult,并按公式(1)計算得到梯形淺基礎豎向承載力系數Nc,計算結果匯總于表2。
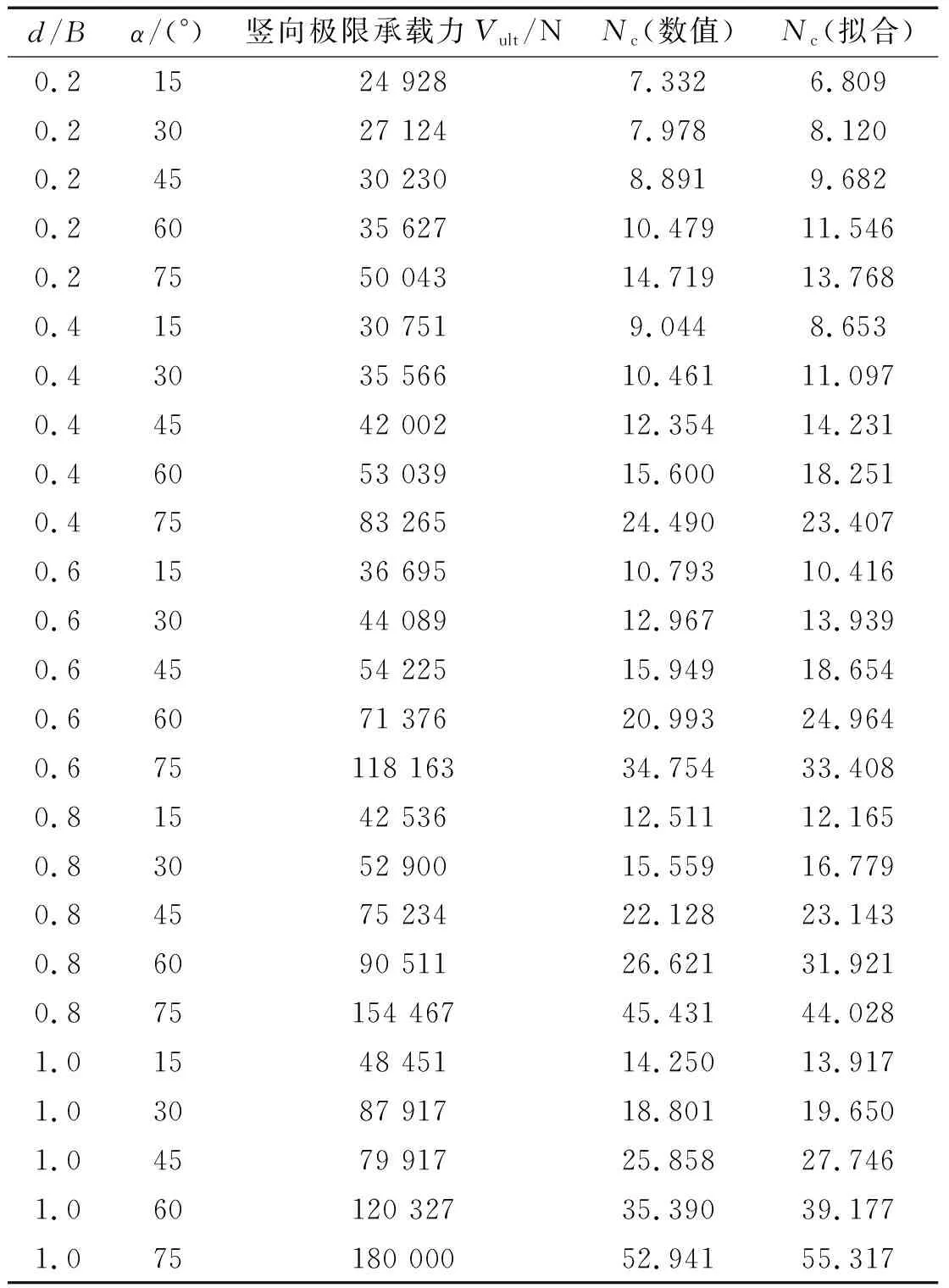
表2 不同傾斜角度α和深寬比d/B下梯形淺基礎豎向承載力系數NcTab.2 The vertical ultimate bearing capacity coefficient of the trapezoidal shallow foundation with different inclinations α and different depth-width ratios d/B
(1)
式中:Nc為梯形淺基礎豎向承載力系數;Vult為梯形淺基礎豎向極限承載力;Su為土體不排水剪切強度;B為梯形淺基礎頂面寬度。
為便于分析梯形淺基礎豎向極限承載力Vult隨基礎傾斜角度α和基礎深寬比d/B的變化關系,將表2中數據整理繪制于圖2。
由圖2-a可知,梯形淺基礎的豎向承載力系數Nc隨著基礎傾斜角度α的增加呈冪指函數形式增長。在基礎豎向承載的土體破壞模式中(如圖3-a所示),基礎下部土體中剛性核的大小主要受限于基礎底面寬度,因此梯形淺基礎的底面寬度為有效控制寬度,對梯形淺基礎的豎向承載破壞模式起決定性作用。在梯形淺基礎頂面寬度B相同的情況下,基礎底面寬度隨著基礎傾斜角度α增加近似呈冪指函數形式增長,故豎向承載力系數Nc也隨著基礎傾斜角度α增加呈冪指函數形式增長。
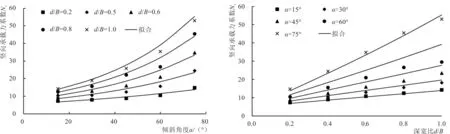
由圖2-b可知,梯形淺基礎的豎向承載力系數Nc隨著基礎深寬比d/B的增加呈線性增長。豎向荷載單獨作用下梯形淺基礎的破壞模式可近似等效為含邊載的無埋深基礎的破壞模式,無埋深基礎底面寬度和梯形淺基礎的底面寬度相同,隨著梯形淺基礎深寬比d/B的增加,等效底面寬度線性增加,等效邊載也成比例增加,故豎向承載力系數Nc也成比例增加。



梯形淺基礎的豎向承載力系數Nc隨基礎傾斜角度α和基礎深寬比d/B的變化關系可采用公式(2)進行擬合,擬合結果如圖2所示。
(2)
式中:d為梯形淺基礎埋深;α為梯形淺基礎傾斜角度;其余符號同前。
2.2 水平極限承載力Hult
相似地采用位移控制法進行加載計算得到不同尺寸梯形淺基礎的水平極限承載力Hult,并按公式(3)計算得到梯形淺基礎豎向承載力系數Nh,計算結果匯總于表3。
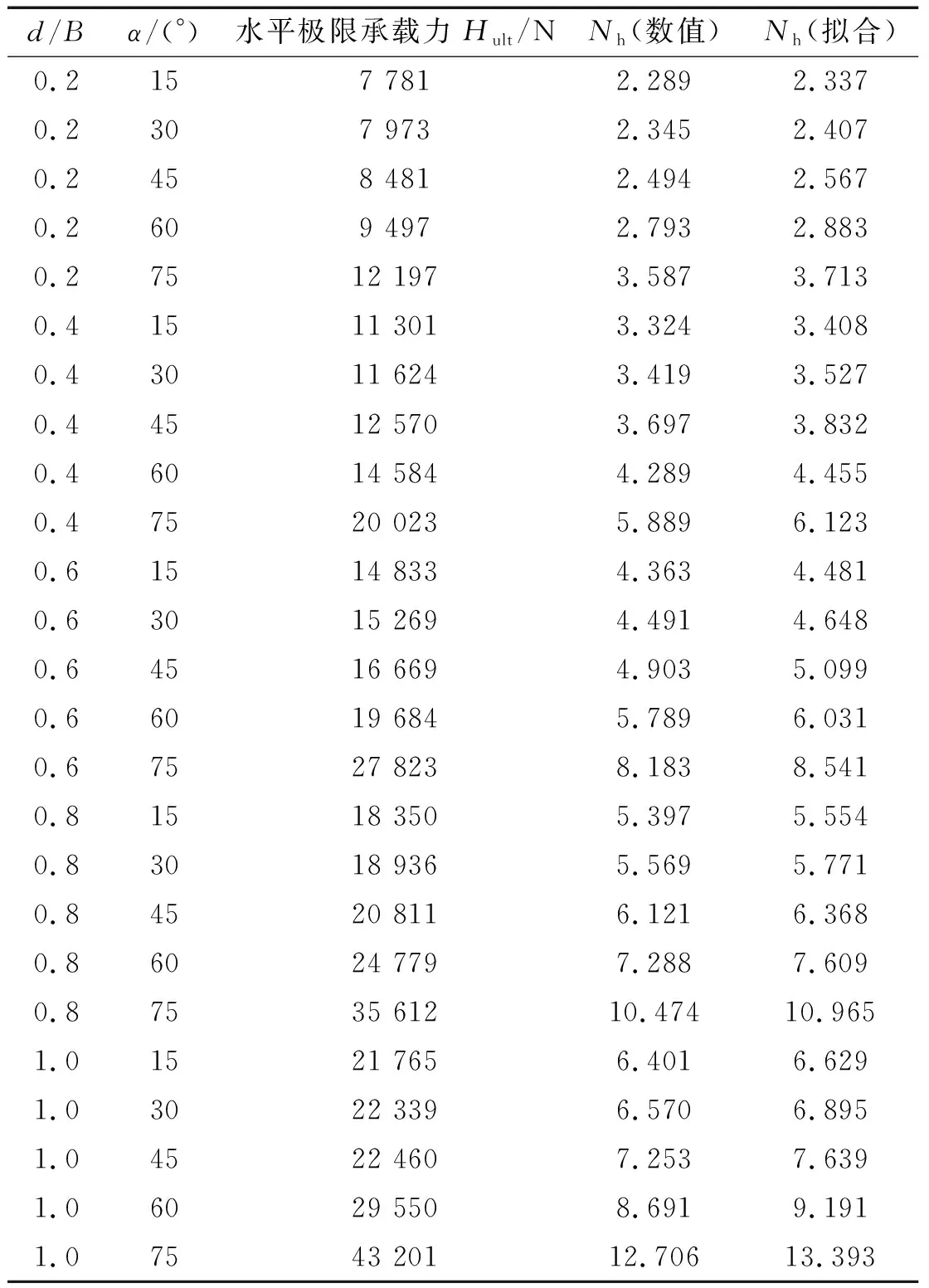
表3 不同傾斜角度α和埋深比d/B下梯形淺基礎水平承載力系數NhTab.3 The horizontal ultimate bearing capacity coefficient of the trapezoidal shallow foundation with different inclinations α and different depth-width ratios d/B
(3)
式中:Nh為梯形淺基礎水平承載力系數;Hult為梯形淺基礎水平極限承載力;其余符號同前。
為便于分析梯形淺基礎水平極限承載力Vult隨基礎傾斜角度α和基礎深寬比d/B的變化關系,將表3中數據整理繪制于圖4。
由圖4-a可知,梯形淺基礎的水平承載力系數Nh隨著基礎傾斜角度α的增加呈冪指函數形式增長。在梯形基礎頂面寬度B相同的情況下,基礎底面寬度隨著基礎傾斜角度α增加近似呈冪指函數形式增長。梯形淺基礎在水平荷載作用下發生水平運動,提供主要水平承載力的基礎底面土體剪切區尺寸(如圖5-a所示)也隨著基礎傾斜角度α增加呈冪指函數形式增加。
由圖4-b可知,梯形淺基礎的水平承載力系數Nh隨著基礎深寬比d/B的增加呈線性增長。由梯形淺基礎的水平破壞模式可知,隨著基礎深寬比d/B增加,梯形淺基礎周圍土體的主動區和被動區也成比例增加,導致基礎水平承載力線性增長。
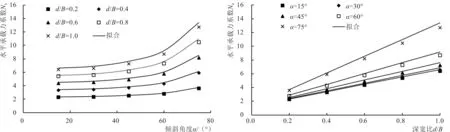
梯形淺基礎的水平承載力系數Nh隨基礎傾斜角度α和基礎深寬比d/B的變化關系可采用公式(4)進行擬合,擬合結果如圖4所示。
(4)
式中:m和n分別為無量綱系數,按表4取值;其余符號同前。



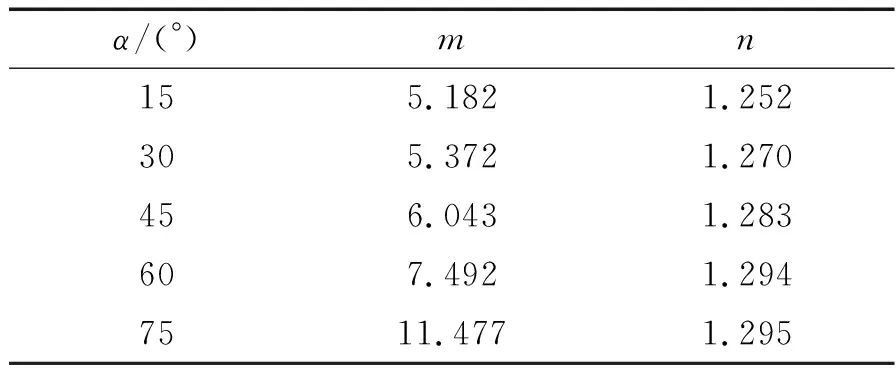
表4 水平承載力計算公式中參數m和n建議值Tab.4 The recommended values of m and n in the calculation formula of horizontal bearing capacity
2.3 彎矩極限承載力Mult
相似地,采用位移控制法進行加載計算得到不同尺寸梯形淺基礎的彎矩極限承載力Mult,并按公式(5)計算得到了梯形淺基礎豎向承載力系數Nm,計算結果匯總于表5。
(5)
式中:Nm為梯形淺基礎彎矩承載力系數;Mult為梯形淺基礎彎矩極限承載力;其余符號同前。
為便于分析梯形淺基礎彎矩極限承載力Mult隨基礎傾斜角度α和基礎深寬比d/B的變化關系,將表5中數據整理繪制于圖6。
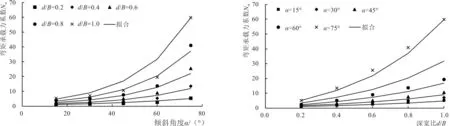
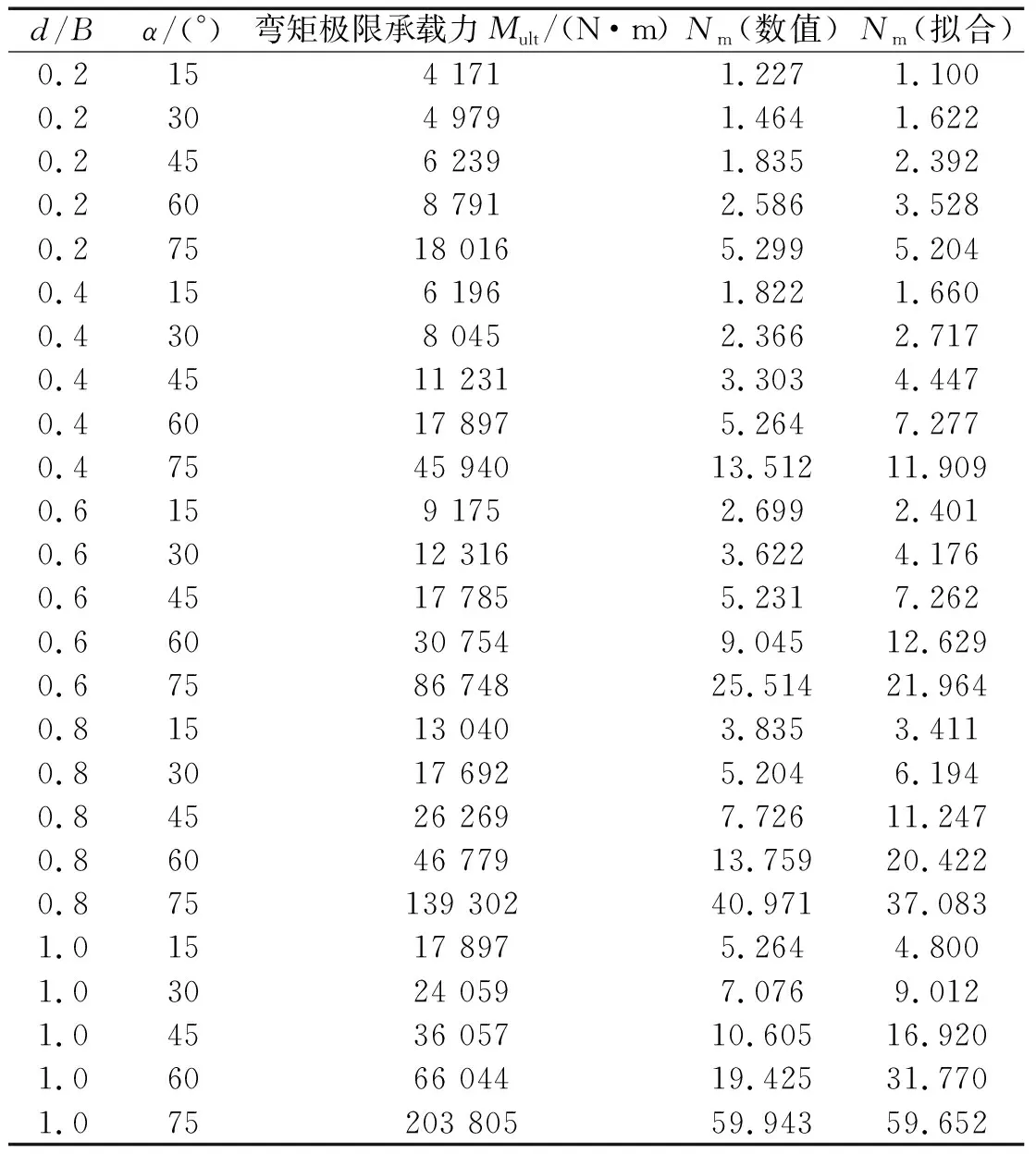
表5 不同傾斜角度α和埋深比d/B下梯形淺基礎彎矩承載力系數NmTab.5 The ultimate bending moment bearing capacity coefficient of the trapezoidal shallow foundation with different inclinations α and different depth-width ratios d/B
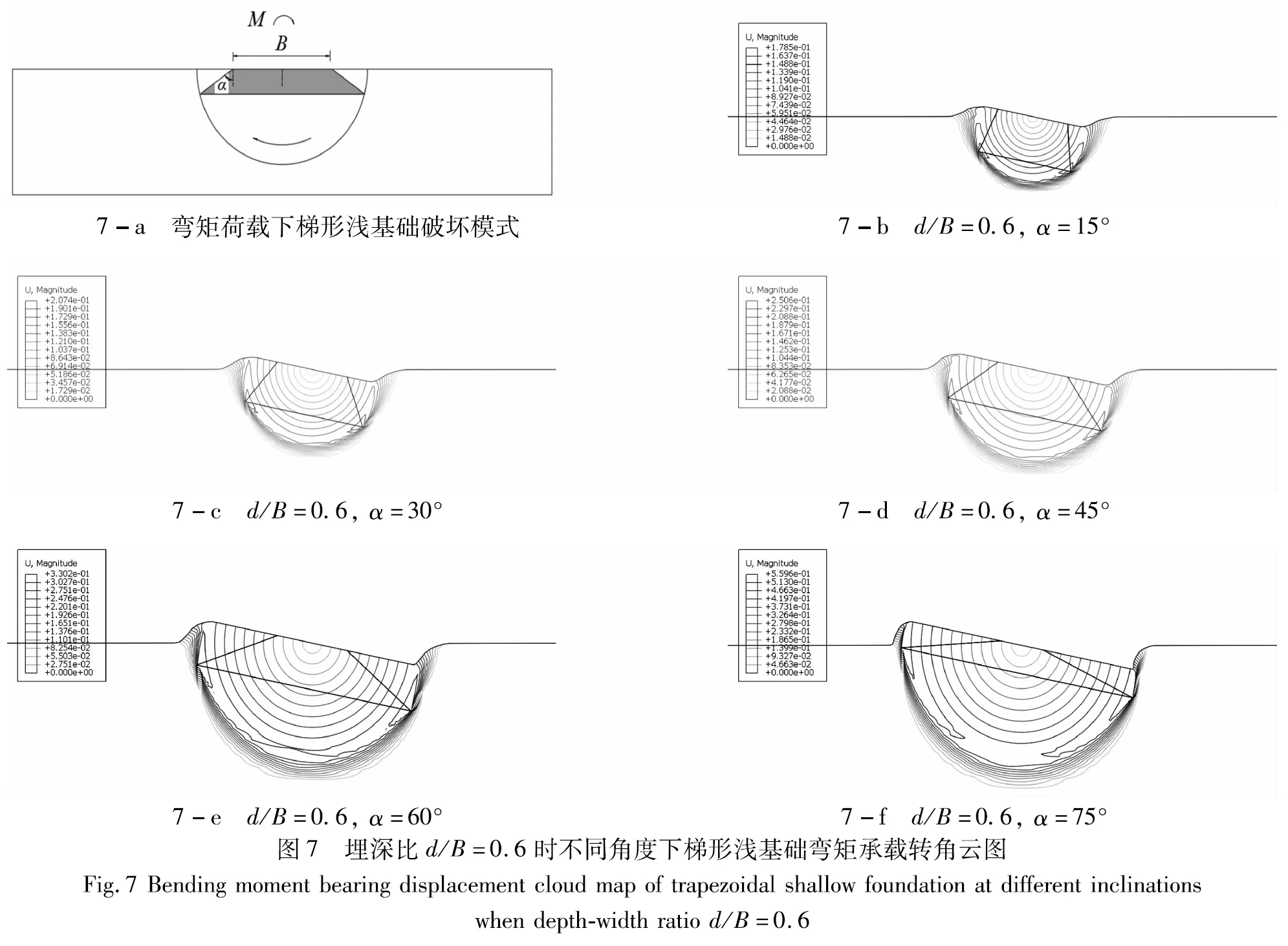
由圖6-a可知,梯形淺基礎的彎矩承載力系數Nm隨著基礎傾斜角度α的增加呈冪指函數形式增長。當梯形淺基礎受到彎矩荷載作用時,基礎下部土體發生繞基礎中心荷載作用點的旋轉運動(如圖7所示),由基礎彎矩承載的土體破壞模式(如圖7-a所示)可知,土體旋轉擾動范圍呈半圓形分布,其半徑由基礎底面寬度決定,因此梯形淺基礎彎矩承載力系數Nm隨著基礎傾斜角度α的變化趨勢同基礎底面寬度一致,均隨著基礎傾斜角度α增加近似呈冪指函數形式增長。
由圖6-b可知,梯形淺基礎的彎矩承載力系數Nm隨著基礎深寬比d/B的增加亦呈冪指函數形式增長。深寬比d/B對彎矩承載力系數Nm的影響原因有待深入研究。
梯形淺基礎彎矩承載力系數Nm隨基礎傾斜角度α和基礎深寬比d/B的變化關系可采用公式(6)進行擬合,擬合結果如圖6所示。
(6)


3 結論
本文提出了梯形淺基礎這一新型結構形式,通過數值模擬的方式探究了深海不排水飽和軟黏土中梯形淺基礎在不同方向荷載單獨作用模式下的承載力特性,運用ABAQUS軟件計算了25組不同傾斜角度和深寬比的二維模型的豎向承載力、水平承載力和彎矩承載力,并給出了歸一化后的承載力系數計算公式。主要結論如下:
(1)豎向承載破壞模式下,決定剛性核尺寸的基礎底面寬度為有效控制寬度,在頂面寬度一定的情況下底面寬度隨傾斜角度α增加呈冪指函數形式增加,豎向承載力系數Nc隨基礎傾斜角度α增加呈冪指函數形式增加;梯形淺基礎可等效為含邊載的無埋深基礎,等效邊載隨基礎深寬比增加呈線性增加,豎向承載力系數Nc隨基礎深寬比d/B的增加呈線性增加。
(2)水平承載破壞模式下,提供主要水平承載力的土體剪切區尺寸由基礎底面寬度決定,基礎底面寬度隨基礎傾斜角度α增加呈冪指函數形式增加,水平承載力系數Nh隨基礎傾斜角度α增加呈冪指函數形式增加;土體主動區和被動區范圍隨基礎深寬比d/B增加而成比例增加,水平承載力系數Nh隨基礎深寬比d/B的增加呈線性增加。
(3)彎矩承載破壞模式下,土體旋轉擾動范圍呈半圓形分布,其半徑由基礎底面寬度決定,擾動范圍半徑隨基礎傾斜角度α增加呈冪指函數形式增加,抗彎承載力系數Nm隨基礎傾斜角度α增加呈冪指函數形式增加;抗彎承載力系數Nm隨基礎深寬比d/B增加亦呈冪指函數形式增加。

