一類具記憶項和非線性阻尼項的雙曲型方程的整體吸引子

張素麗，張建文，王海燕

(1.太原理工大學機械與運載學院，山西太原030024;2.太原理工大學數學學院，山西太原030024;3.太原科技大學應用科學學院，山西太原030024)

1.引言

波動方程是偏微分方程中重要的一類方程，對波動方程的數學研究能幫助我們更加準確深刻地描述和理解物體的運動情況和物理規律.關于波動方程的研究已有很多著作.[1－3]Giorgi等[4]研究了只有記憶項的波動方程

的整體吸引子的存在性.記憶項是反應系統的過去狀態對系統的未來行為的影響，是材料的某種“記憶”性能，很多粘彈性材料都有這種“記憶”性能.

MA和ZHONG[5]研究了具有記憶項和弱阻尼項的波動方程

的整體吸引子的存在性.由于在物體的運動過程中，阻尼是不可避免的，并且阻尼對物體的運動有著巨大的影響，所以研究具有阻尼項和記憶項的波動方程有很重要的物理意義.

Park等[6]研究了具有記憶項和非線性阻尼項，即阻尼項以非線性次數增長情形下的波動方程

的整體吸引子的存在性.

Kirchhoff[7]于1883年研究可拉伸弦的振動問題時，建立了下列模型

與經典波動方程相比，這類方程能更準確地描述弦自由振動問題.因此，后人將這類方程命名為Kirchhoff方程.關于此類問題解的存在性證明可參考文[8-10].2011年Lazo[11]運用經典的Galerkin方法證明了具有記憶項的Kirchhoff方程

的整體弱解的存在性.

受以上文章的啟發，我們研究如下一類具有記憶項和非線性阻尼項的Kirchhoff波動方程的整體吸引子的存在性.

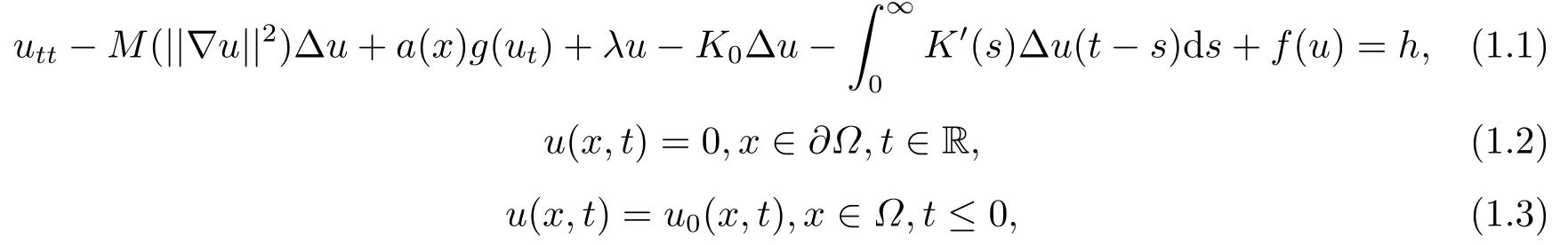
Ω是RN中具有光滑邊界?Ω的有界區域，其中M(s)=a+bs，a，b＞0，g(ut)是阻尼項，f(u)是源項.關于a(x)，g(ut)，f(u)的假設我們將在后面給出，h是L2中的函數.

我們采用文[4-6]中的定義：

對上式求導，我們可得

所以

令μ(s)=-K′(s)，K(∞)=1，方程(1.1)變為

初邊值為

2.預備知識

我們首先給出證明過程中用到的一些假設:

1)關于記憶項μ的假設:

(h1)μ(s)∈C1(R)∩L1(R)，?s∈R+;

(h3)μ(s)≥0，μ′(s)≤0;

(h4)μ′(s)+k1μ(s)≤0，?s∈R+，其中k1＞0.

2)函數a(x)滿足

其中α0是常數.

3)函數f∈C1(R)，滿足

當n≤2時，0＜p＜∞;當n＞2時，λ1是中的第一特征值.

4)函數g滿足

當n≤2時，1≤q＜∞;當n＞2時，1≤q≤.

接下來，我們給出本文用到的空間

其內積和范數為

我們的分析是基于如下空間

并對其賦予以下的范數

利用經典的Galerkin方法，我們可得到如下關于系統(1.7)-(1.10)解的存在唯一性，具體可參考文[6，14].

引理2.1[6，14]假設1)-4)都成立，若z0=(u0，v0，η0)∈H，則系統(1.7)-(1.10)存在唯一弱解z=(u，ut，η)，對所有的T＞0都滿足z∈C([0，T]，H).

引理2.2[13]設g(.)滿足(2.4).則對任意δ＞0，存在C(δ)＞0，滿足

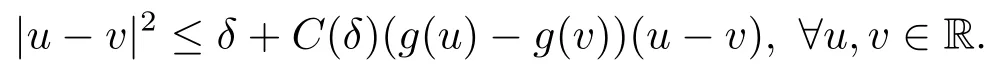
3.吸收集

本節中，我們將證明系統(1.7)-(1.10)在H中存在有界吸收集.本文中(·，·)，||·||分別代表L2中的內積和范數，Ci表示不同的正常數.

引理3.1在引理2.1的假設下，系統(1.7)-(1.10)在空間H中存在有界吸收集.

證方程(1.7)與ut作L2中內積，得

我們令

由(3.1)，(3.2)我們可知

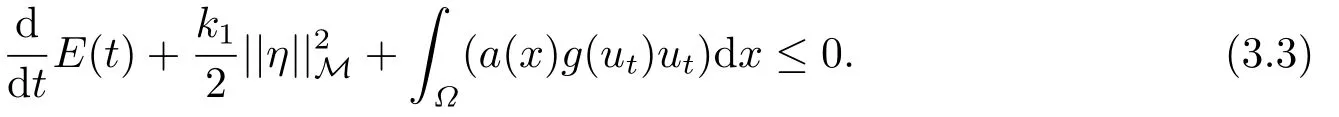
對上式，我們在[0，T]上積分，由假設2)，4)，我們有

由假設2)，我們可知存在λ＞λ′＞0，以及C0滿足下式

選擇足夠小的ε＞0，則

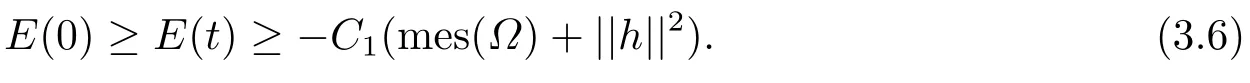
由(3.3)，(3.6)，可得

接下來，方程(1.7)與v=ut+δu作L2中內積，我們可得

設

所以

利用(3.5)和Young不等式，

選擇足夠小的δ，ε，使得，則有

由假設2)，4)，我們可知存在δ＞0和C(δ)＞0，使得下式成立

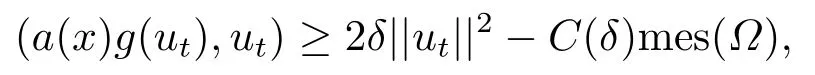
由Young不等式，可得

由假設4)，我們有

所以

其中C是與s無關的常數.

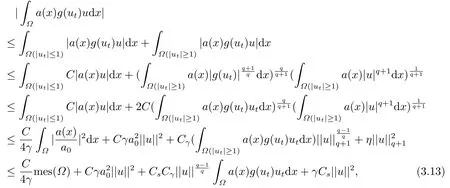
其中a0=supx∈Ω a(x)，γ是常數.由(3.5)(3.10)(3.11)(3.13)，我們有

選擇足夠小的γ，使得可知

其中CE(0)由δ，Cγ，Cs，E(0)共同決定，是依賴于δ，Cδ，C0，C的常數.

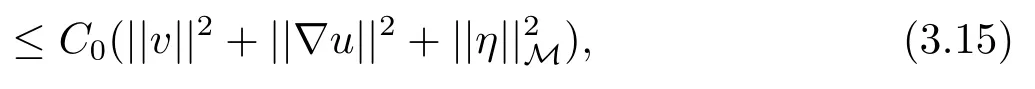
對(3.8)在(0，t)上積分，結合(3.7)，(3.9)，(3.14)，我們可得

其中δ′=min{δ，k1}.

因此B0是一個有界吸收集，定義

B1就是所需的有界吸收集.證畢.

4.整體吸引子

本節我們將證明系統整體吸引子的存在性.我們定義

引理4.1[12]耗散動力系統(H，S(t))具有一個緊的整體吸引子當且僅當它是漸進光滑的.

引理4.2[12]假設對任意的有界正不變集B?H和任意的ε＞0，存在T=T(ε，B)，使得

這里ΦT:B×B→R，對任意{zn}n∈N?B，滿足

那么半群S(t)是漸進光滑的.

接下來，我們利用先驗估計來證明系統的漸進光滑性.

首先，方程(4.2)與ω作L2中內積，有

對上式在[0，T]上積分

由Young不等式，我們有

緊接著，方程(4.2)與ωt作L2中內積，得

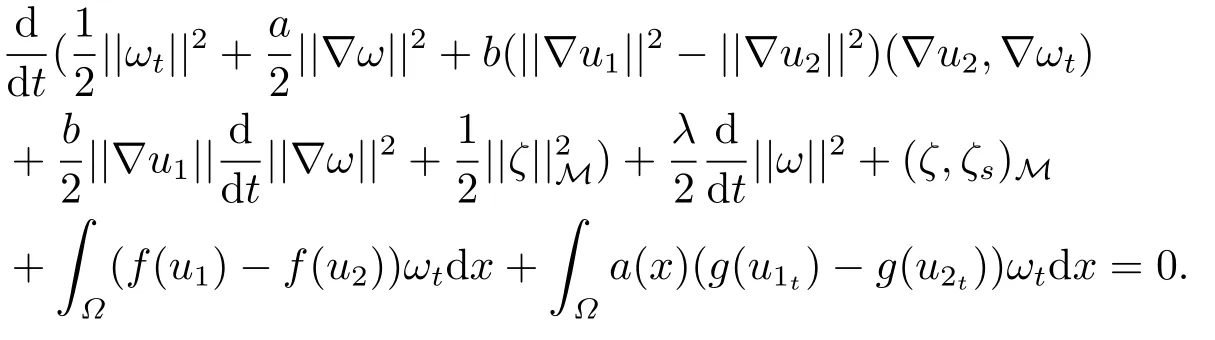
令

由于

所以

(4.6)在[s，T]上積分，其中0≤s≤t，

(4.7)關于s在[0，T]上積分，得

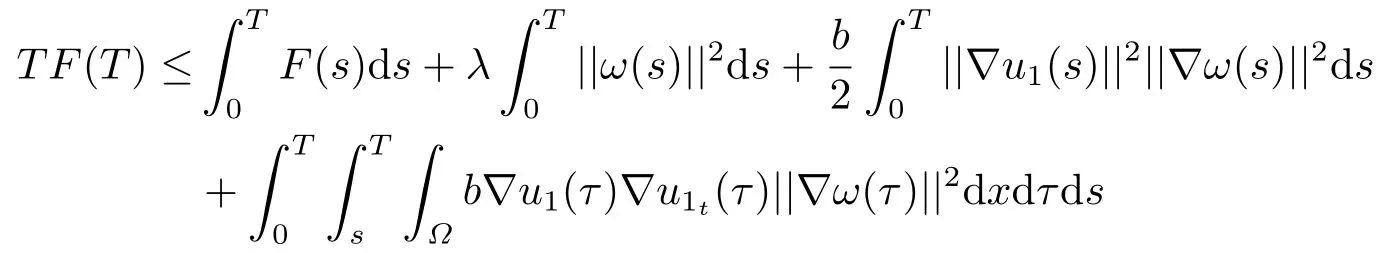
將(4.6)在[0，T]上積分，得

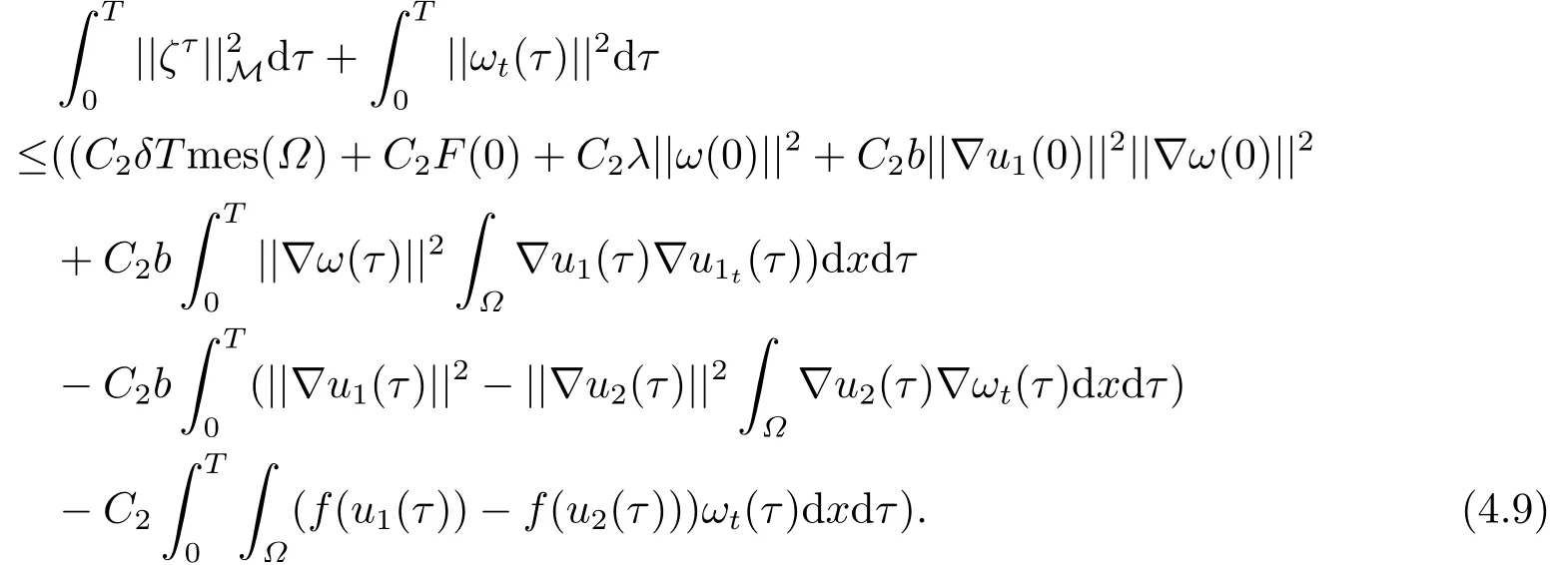
由(4.4)(4.5)(4.9)，我們有

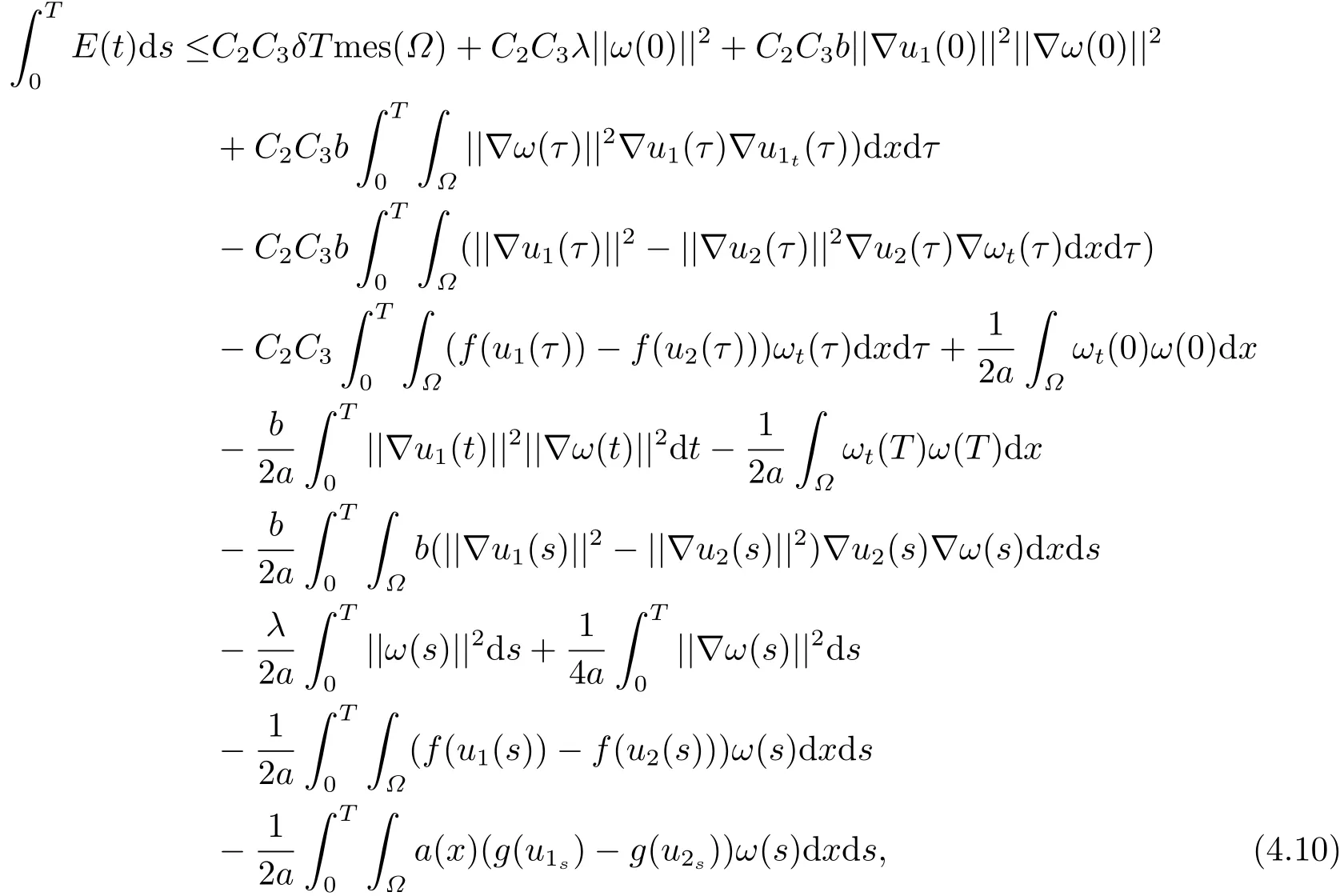
由(3.7)及吸收集的存在性，我們有

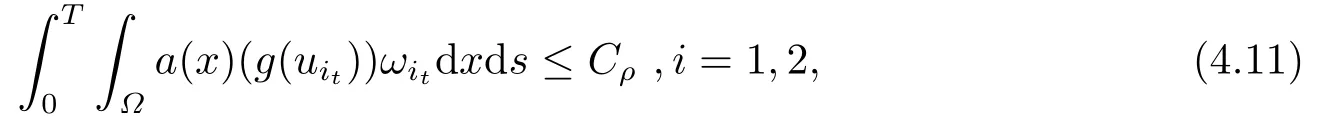
其中Cρ由mes(Ω)，||h||2及B0的半徑共同決定.

類似于(3.13)，我們有

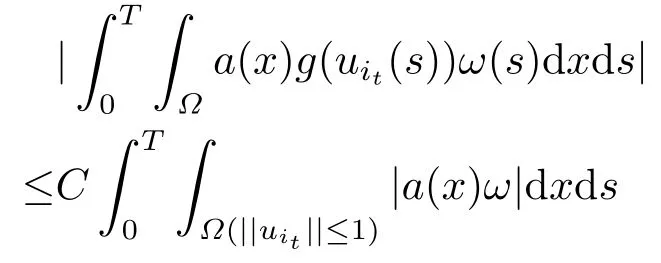
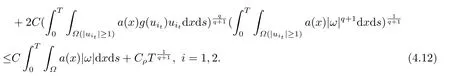
結合(4.8)(4.10)(4.12)，我們有

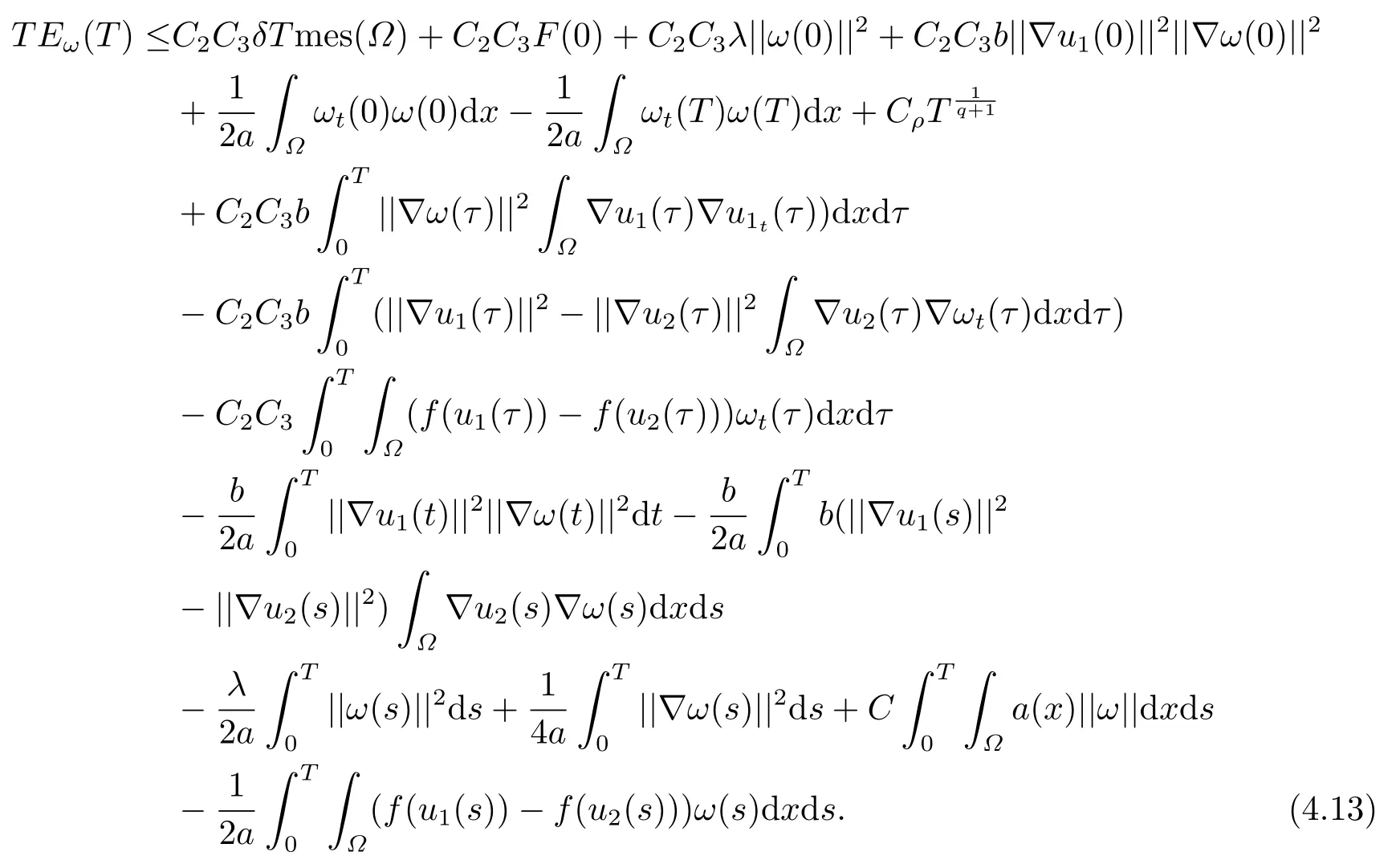
令

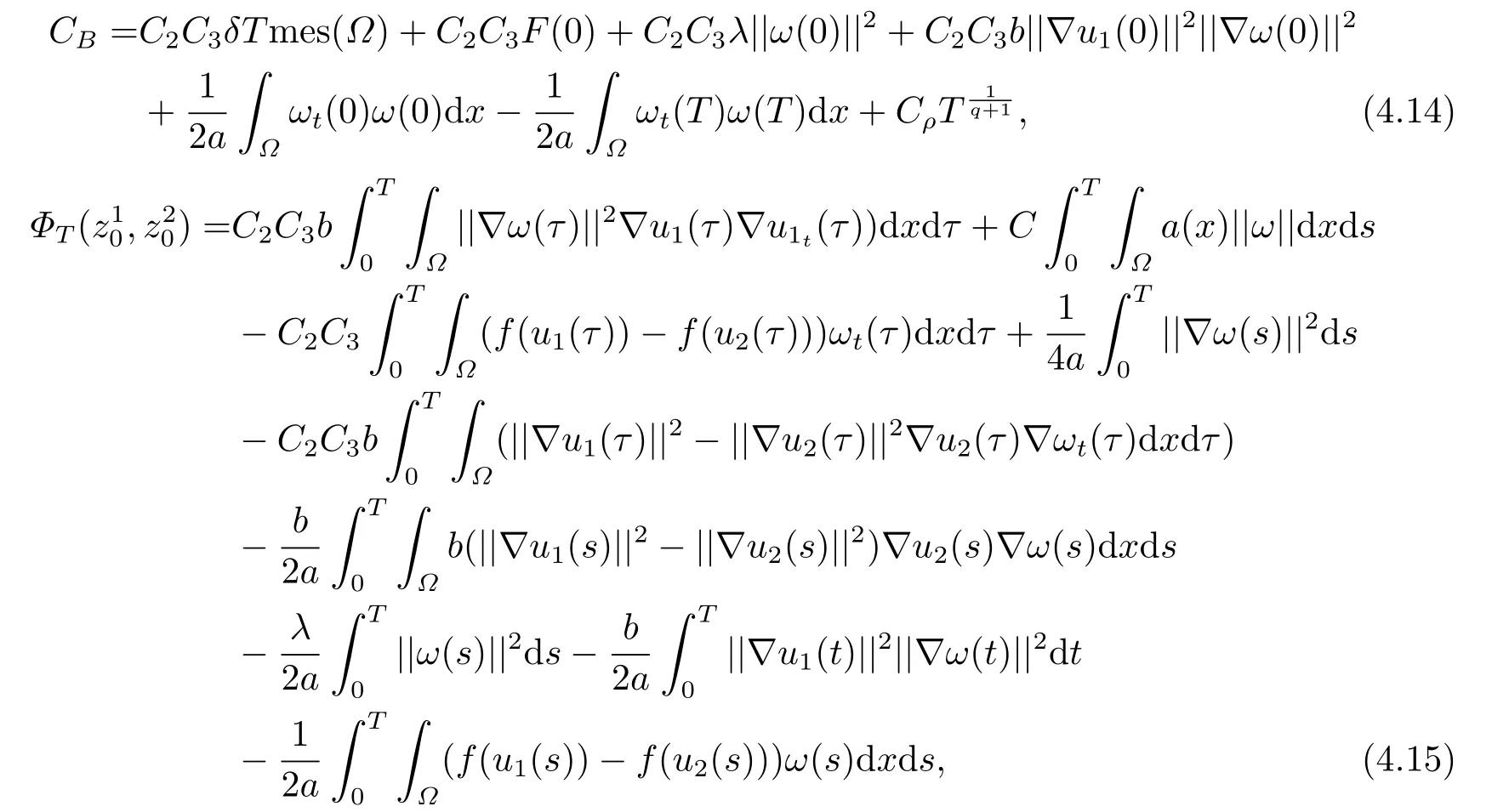
則我們有

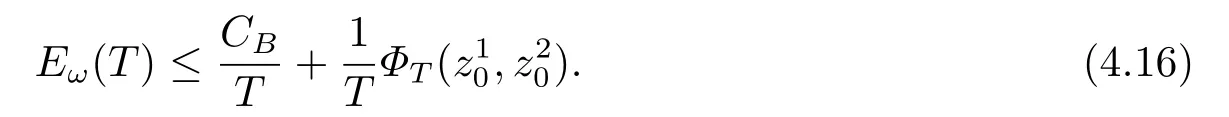
接下來，我們利用引理4.2來證明半群{S(t)}t≥0在H中是漸近光滑的.

定理4.1在假設1)-4)下，系統(1.7)-(1.10)所對應的半群{S(t)}t≥0在H中是漸近光滑的.

證由于半群{S(t)}t≥0存在有界吸收集，我們選取并且選取足夠大的T使得于是，由引理4.2，我們只需證明，(4.15)中定義的對每個固定的T，(4.1)式恒成立.這里(un，unt，ηn)是相應于初值=1，2的解，我們有和其中.

因為B1是H中的正不變集，不失一般性，我們有

緊接著，由(4.17)，我們可得

最后，類似于文[6]，我們有

結合(4.21)-(4.29)和引理4.2可知定理4.1成立.證畢.

定理4.2若假設1)-4)成立，系統(1.7)-(1.10)在H中存在整體吸引子.

證由引理3.1和引理4.1可知系統存在整體吸引子.證畢.