共振情形下一類非合作反應堆數(shù)學模型正解的存在性

陳瑞鵬，劉佳音，張光晨

(北方民族大學數(shù)學與信息科學學院，寧夏銀川750021)

1.引言

本文研究二階非合作微分系統(tǒng)

正解的存在性，其中c，d為正常數(shù)，非線性項f∈C([0，1]×[0，∞)，R)且g∈C([0，∞)，[0，∞)).因此，系統(tǒng)(1.1)是一個半正系統(tǒng)，同時由Neumann邊界條件易見系統(tǒng)(1.1)為共振系統(tǒng).

系統(tǒng)(1.1)與反應擴散系統(tǒng)

的穩(wěn)態(tài)形式有著緊密聯(lián)系.反應擴散系統(tǒng)(1.2)旨在描述密閉容器中與中子通量、反應堆溫度等因素密切相關(guān)的核反應過程，其中Ω是Rn(n≥1)中具有C2+θ(θ∈(0，1))光滑邊界?Ω的有界連通區(qū)域，且代表密閉容器，n為?Ω上的單位外法向量.實際應用方面，未知函數(shù)u和v分別表示中子通量與反應堆的溫度，b，c，d均為常數(shù)且滿足b∈[0，∞)，c，d∈(0，∞)，u0，v0∈C為初始條件.通過添加溫度的擴散與線性反饋，模型(1.2)改進了由Kastenberg和Chambr[10]提出的反應堆數(shù)學模型

注意到模型(1.2)中的Neumann邊界條件意味著快中子不能穿越容器壁，而且密閉容器的邊界絕熱，這代表更加貼近實際的情形.

近年來，諸多學者對模型(1.3)正解的存在性及相關(guān)性質(zhì)做了深入研究，并獲得了許多深刻的結(jié)果[1，7，10，12，14－15].同時，多位學者致力于研究模型(1.3)在一維情形下正解的存在性問題，如WANG和AN[16－18]，LI和LI[11]，CHEN和MA[3－4]等.然而據(jù)我們所知，上述大多數(shù)文獻聚焦于研究帶有Dirichlet邊界條件的模型(1.3)，其中Dirichlet邊界條件意味著密閉容器的邊界上沒有快中子且恒溫，是一種較為理想的情形，但是在Neumann邊界條件下的研究成果相對較少.此外，文[3-4，16-18]只對模型的非共振情形進行了研究，而且所得正解的存在性結(jié)果極大程度上依賴于非線性項的正性.鑒于此，本文將在共振情形下建立非合作半正系統(tǒng)(1.1)正解的存在性結(jié)果.本文總假設

(H1)f∈C([0，1]×[0，∞)，R)，g∈C([0，∞)，[0，∞)).

注1.1(H1)蘊含了非線性項f是變號且下無界的，這將對系統(tǒng)(1.1)正解存在性的研究帶來較大困難.此外，本文將首次建立共振情形下反應堆數(shù)學模型正解的存在性及全局分歧結(jié)果，所得結(jié)論將進一步豐富反應堆數(shù)學模型的相關(guān)理論.對于其它半正問題和共振問題的研究，可參見文[2，8-9，13，19]等.

本文結(jié)構(gòu)作如下安排:在第二部分，將給出一些所需的符號及預備知識;第三部分將敘述并證明系統(tǒng)(1.1)正解的存在性定理，同時給出一些相關(guān)結(jié)果和注記.

2.預備知識

若函數(shù)p∈C[0，1]在[0，1]上嚴格為正，則記為p?0.令K(t，s)為邊值問題

的格林函數(shù)，則不難驗證K(t，s)＞0，?(t，s)∈[0，1]×[0，1].此時，

等價于算子方程

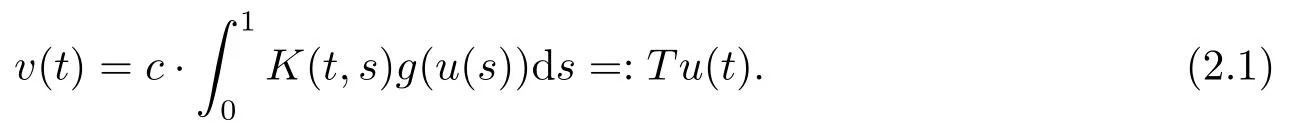
由假設(H1)易知T:C[0，1]→C[0，1]是一個全連續(xù)算子，而且系統(tǒng)(1.1)可轉(zhuǎn)化為

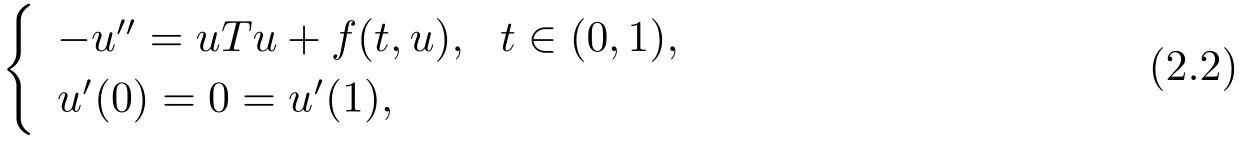
這顯然是一個共振問題.

在后續(xù)討論中，給定函數(shù)

我們將研究與(2.2)等價的積分微分方程

事實上，若問題(2.4)存在一個正解u，則由(H1)和(2.1)可知原系統(tǒng)(1.1)必存在正解(u，v).這里稱(u，v)為系統(tǒng)(1.1)的一個正解，若(u，v)滿足(1.1)且u?0，v?0.眾所周知，問題(2.4)等價于積分方程

其中G(t，s)為線性邊值問題

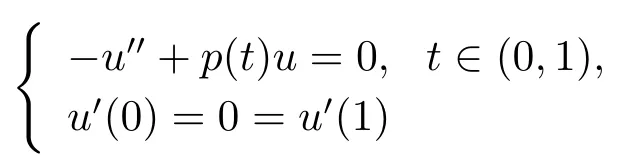
的格林函數(shù).顯然，G(t，s)在[0，1]×[0，1]連續(xù)且

令

則σ∈(0，1).定義錐

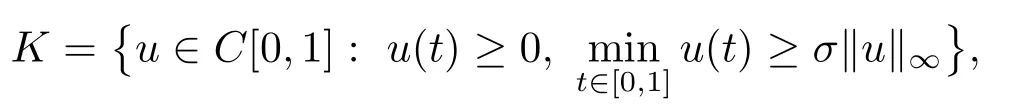
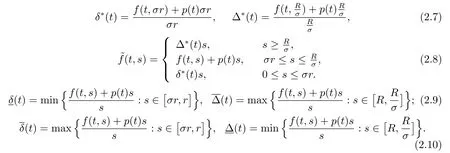
下面，我們給出本文所采用的主要工具.

假設E是實的Banach空間，其范數(shù)為‖·‖.假設K是空間E中的一個錐.稱非線性映射A:[0，∞)×K→E是正的，若它滿足A([0，∞)×K)?K.稱上述映射A為K-全連續(xù)的，若A連續(xù)且把[0，∞)×K中的有界子集映射為空間E中的相對緊集.稱定義于E上的線性正算子V是算子A的線性弱函數(shù)，若它滿足A(λ，u)≥λV(u)，(λ，u)∈[0，∞)×K.記r(B)為定義在空間E上的連續(xù)線性算子B的譜半徑.

引理2.1[5]若下列條件成立:

(i)錐K有非空內(nèi)部且滿足;

(ii)A:[0，∞)×K→E是一個正的K-全連續(xù)算子.

且A(λ，u)=λBu+F(λ，u)，其中B:E→E是r(B)＞0的線性強正緊算子，F(xiàn):[0，∞)×K→E滿足當‖u‖→0時，‖F(xiàn)(λ，u)‖=°(‖u‖)對λ局部一致地成立.

則在

中存在無界連通子集C，使得(r(B)－1，0)∈C.進一步，若存在A的線性弱函數(shù)V和(μ，y)∈(0，∞)×K，使得‖y‖=1及μV y≥y成立，則C位于S∩([0，μ]×K)中.

方便起見，記λ*(η)為特征值問題

的主特征值，其中函數(shù)p由(2.3)給出.由Krein-Rutman定理[6]可知當η?0時λ*(η)＞0.此外，λ*(η)是簡單的且對應的特征函數(shù)滿足ψ*(η)?0.

3.主要結(jié)果及證明

為了敘述本文的主要結(jié)果，假設

(H2)存在正常數(shù)R＞r，使得

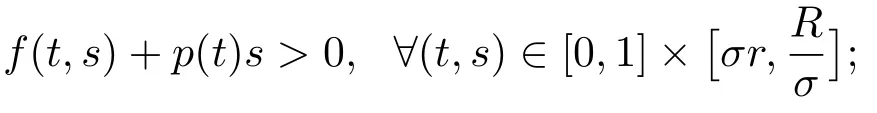
定理3.1假設(H1)，(H2)，(H3)成立.若條件

之一滿足，則系統(tǒng)(1.1)至少存在一個正解.

證我們只證明情形(i)，情形(ii)的證明完全類似.

考慮輔助問題

其中λ∈[0，∞)為參數(shù).由第二部分的討論易知(3.1)等價于算子方程

運用假設(H2)，(H3)并結(jié)合函數(shù)～f的定義，不難驗證A(K)?K且A:K→K是一個全連續(xù)算子.由(2.8)易得

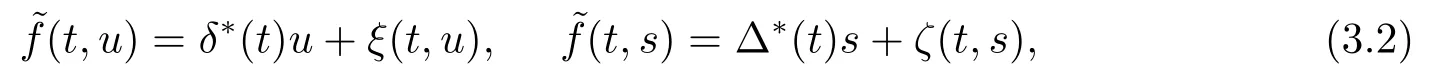
其中

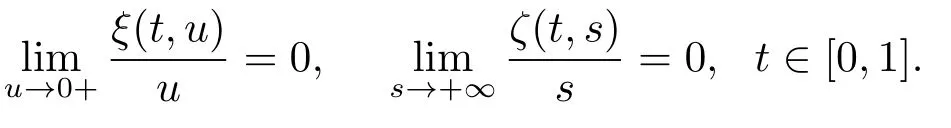
從而(3.1)可改寫為

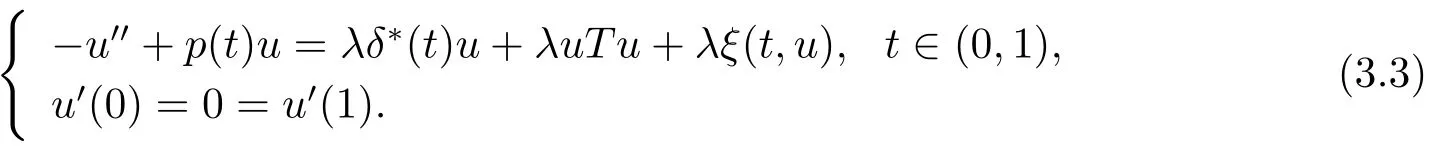
定義Banach空間E=u∈C1[0，1]:u′(0)=0=u′(1)，其范數(shù)為‖u‖=max{‖u‖∞，‖u′‖∞}.記

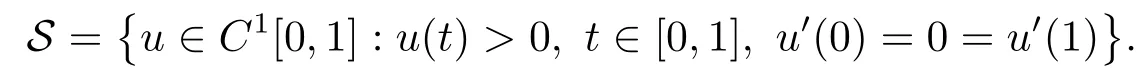
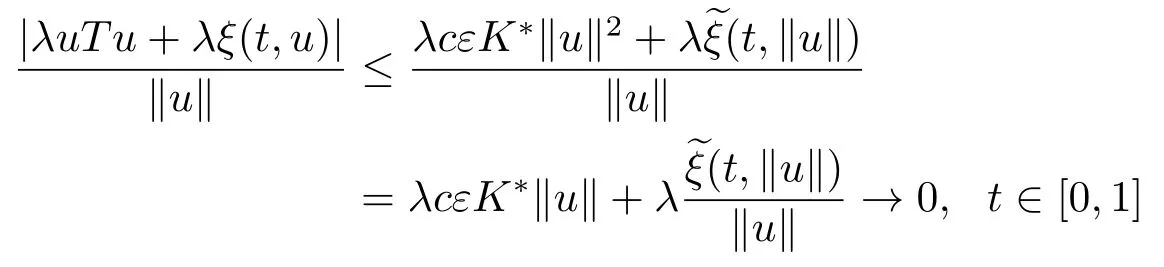
對λ局部一致地成立，其中

因此，由引理2.1可知存在(3.3)解的連通分支C，它在S中連接(λ*(δ*)，0)到無窮遠處.此外，C{(λ*(δ*)，0)}?S.

下面，分兩步來完成本定理剩余部分的證明.

第一步連通分支C在S中連接(λ*(δ*)，0)與(λ*(Δ*)，∞).

事實上，若能夠證明C在S中連接(λ*(δ*)，0)與(λ*(Δ*)，∞)，則C必會穿過超平面{1}×E，從而問題(3.3)至少存在一個正解(1，u).

假設{(λk，uk)}?C且滿足

我們宣稱{λk}有界.反設λk→∞，k→∞.因為(λk，uk)∈C，所以

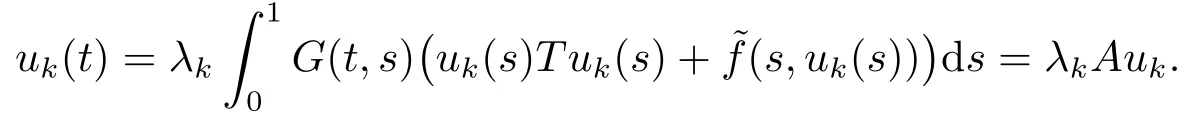
這與‖vk‖∞=1矛盾.因此{λk}有界.

此時，由(3.4)及上述宣稱可得‖uk‖→∞，k→∞.進一步，運用假設(H1)-(H3)，并通過與文[3]中引理2.5證明中類似的討論可知當‖uk‖→∞時必有‖uk‖∞→∞，從而{(λk，uk)}滿足

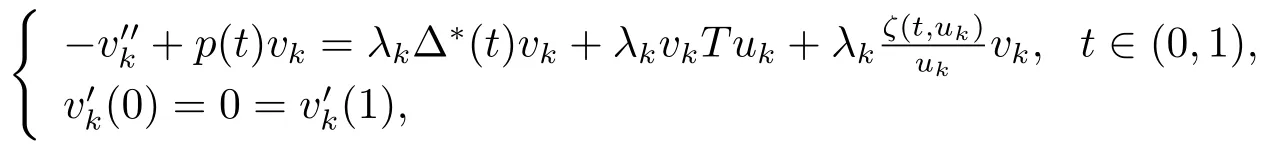
這等價于

借助(2.8)及(3.2)，經(jīng)簡單估計可得

這表明存在不依賴于k的函數(shù)χ∈C[0，1]，使得

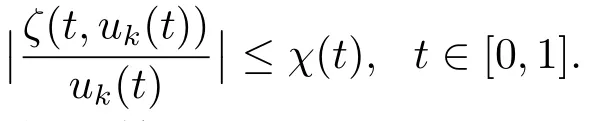
此外，由假設(H3)易得{Tuk}有界.于是，

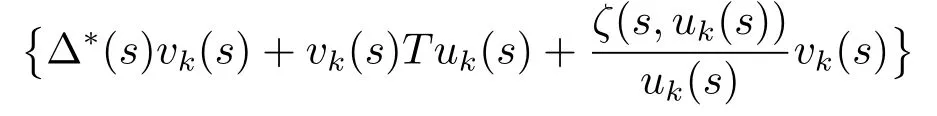
在空間C[0，1]中一致有界.容易看到

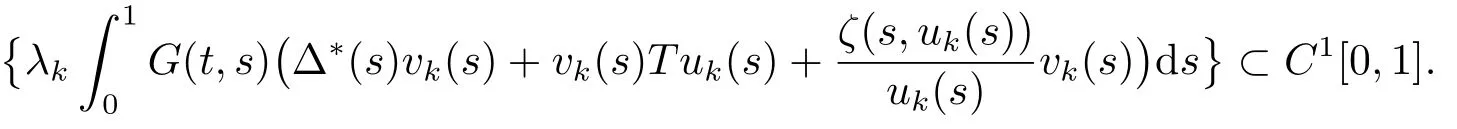
又因為C1[0，1]緊嵌入C[0，1]，故存在{vk}的子列(仍記為自身)及∈C[0，1]，∈[0，∞)，使得vk→且λk→k→∞.由假設(H3)及Lebesgue控制收斂定理可得

第二步u是共振問題(2.2)的解.

顯然，只需證明

不存在能夠滿足‖u‖∞＜r或的正解u.事實上，若上述結(jié)論成立，則由函數(shù)的定義可得從而(3.5)將退化為原共振問題(2.2).

反設(3.5)存在一個滿足‖u‖∞＜r的正解u，則由(2.8)及(2.9)可得

因為

且

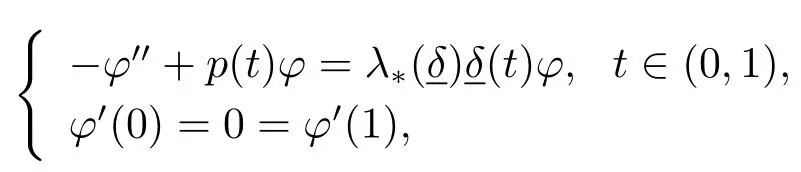
其中φ是主特征值對應的主特征函數(shù).顯然，φ?0.運用(3.6)和假設(H1)，并通過簡單的積分運算估計可得

因為u是(3.5)的正解，所以

又因為

其中ψ為λ*對應的特征函數(shù)且顯然滿足ψ?0.由(3.7)和假設(H3)可得

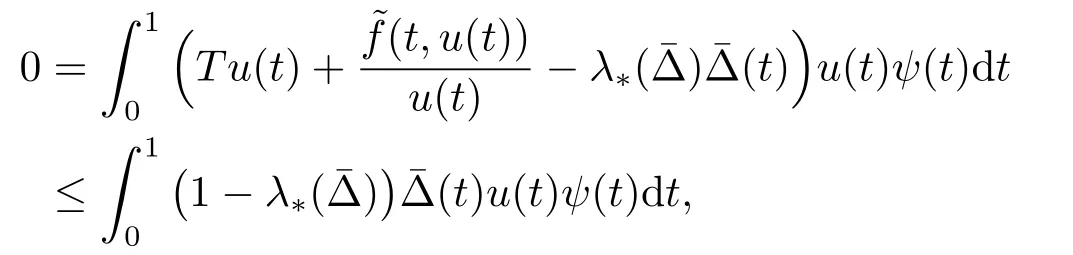
故這與假設矛盾.

綜上所述，共振問題(2.2)存在一個正解u.進一步，由(2.1)可知原系統(tǒng)(1.1)至少存在一個正解(u，v).

最后，我們給出一些相關(guān)結(jié)果.

若考慮快中子不能穿越容器壁且反應堆與外界有熱交換的情形，則適當?shù)倪吔鐥l件為

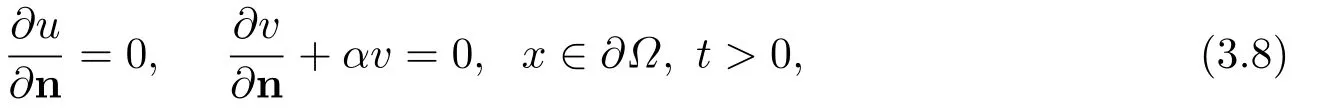
其中α＞0為熱交換系數(shù).相應地，有非合作系統(tǒng)

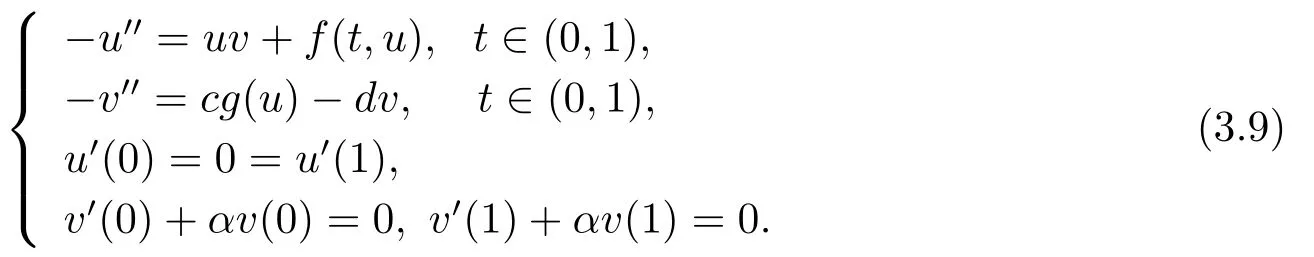
在(H1)-(H3)和一些自然的假設之下，通過與本文第二部分以及定理3.1的證明中完全類似的討論，我們不難得到

定理3.2假設(H1)-(H3)成立.若條件

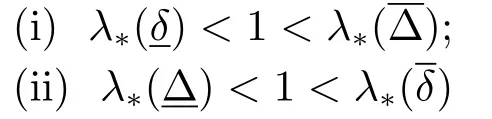
之一滿足，則系統(tǒng)(3.9)至少存在一個正解.

注3.1對于帶Neumann邊界條件或邊界條件(3.8)的橢圓系統(tǒng)

本文所采用的討論方法仍然適用于研究其徑向正解的存在性.