磁力預緊緩沖器的力學特性及緩沖性能研究
曾澤璀, 張 磊, 閆 明, 張春輝
(1. 沈陽工業大學 機械工程學院,沈陽 110870; 2. 海軍研究院,北京 100161)
振動激勵通常會對工程振動系統產生不利影響。一般的振動激勵源主要包括動力源設備產生的周期振動、不平整路面所造成的汽車整體結構的隨機振動等。除此之外,還有一些瞬時振動,例如碰撞、爆炸、沖擊等,它是由短時間的瞬間激勵載荷作用產生,通常伴隨著較大的作用力和位移[1]。振動和沖擊能夠導致一系列問題,例如敏感設備的損壞、設備定位精度下降、操作人員的不適感等[2]。因此工程振動領域中一些較為敏感的設備,如高精度加工機器、精確導航設備、汽車座椅、航天電子設備等等,都需要安裝隔振器或者緩沖器[3]。
傳統被動緩沖器主要由彈性元件和阻尼元件組成,不包含其它組成元件。由于沖擊具有載荷幅值高和瞬間產生的特點,僅具有線性特征的緩沖器已經不能夠滿足緩沖要求。因此后來不斷出現具有非線性特征的被動緩沖器,例如,鋼絲繩緩沖器、預緊緩沖器、準零剛度緩沖器等[4-7]。這些緩沖器的剛度特性都具有軟化特征,從而使得系統具有高靜態低動態特征,大量的研究表明具有軟化特征的緩沖器比較適合于沖擊隔離。
慣導設備是保證艦船航行關鍵設備,在常規航行條件下,慣導設備需與安裝基礎之間保持剛性連接。但是艦船在海上行駛過程中容易受到魚雷攻擊,由魚雷所產生的非接觸爆炸將對艦船產生沖擊,沖擊經由船體結構傳遞至慣導設備,從而導致慣導設備遭受沖擊作用。傳統的緩沖器難以實現慣導設備的緩沖要求,而預緊緩沖器不僅能夠保證慣導設備在小激勵作用下保持剛性連接,而且能在強烈的水下非接觸爆炸環境下起到緩沖作用。
傳統的預緊緩沖器,通常是利用特殊結構將彈性元件進行預壓縮,從而產生初始預緊力,當沖擊載荷大于預緊力時,緩沖器才開始變形緩沖[8]。但是這類型緩沖器的緩沖效果受到系統彈性元件特性的影響,當緩沖器的彈性元件剛度較小時,需要通過較大的初始變形獲得預緊力,這將會導致緩沖器結構尺寸較大;當緩沖器的剛度較大時,雖然通過較小的初始變形就能獲得一定預緊力,但是在沖擊作用下容易產生更大的加速度響應。因此在傳統預緊緩沖器的設計過程中,彈性元件剛度、初始預緊力與系統加速度響應之間存在一定的妥協關系。
針對上述問題,本文提出一種磁力預緊緩沖器,該緩沖器通過磁鐵組件產生預緊力,并在變形階段設置較低剛度的彈性元件,從而改善了傳統彈性元件、初始預緊力以及系統加速度響應之間的妥協關系,提高緩沖性能。接下來,首先對磁力預緊緩沖器的工作原理進行說明,建立緩沖器力學模型,利用諧波平衡法求解磁力預緊緩沖器模型,獲得該系統的方程解;然后,通過數值計算獲得磁力預緊緩沖器的沖擊響應規律,分析預緊力和系統剛度對緩沖器沖擊響應的影響;接著,將磁力預緊緩沖器與傳統預緊緩沖器的沖擊響應進行對比分析;最后,利用跌落試驗機對磁力預緊緩沖器原理樣機進行沖擊試驗,對仿真結果進行驗證。
1 磁力預緊緩沖器原理
1.1 磁力預緊緩沖器原理
所設計的磁力預緊緩沖器需要滿足以下基本要求:在初始平衡位置具有一定預緊力,且該預緊力小于設備所承受的加速度上限。滿足上述要求的緩沖器不僅能夠降低設備所受到的沖擊損傷,還能夠保證設備在小幅值干擾激勵下保持穩定。
磁力預緊緩沖器的簡化原理如圖1所示,緩沖器主要包括:1.質量塊,2.彈簧,3.懸浮支架,4.阻尼器,5.基礎以及四組永磁鐵。四組磁鐵的編號分別為①、②、③和④,當緩沖器處于初始平衡位置時,每組磁鐵中的兩個磁鐵處于異極相吸的狀態,且每組中上磁鐵均為N極,下磁鐵均為S極;N極磁鐵均安裝在懸浮支架上,S極磁鐵分別安裝在彈簧和基礎上。緩沖器初始平衡狀態如圖1(a)所示,向下運動和向上運動的最大變形位置分別如圖1(b)和圖1(c)所示。

圖1 磁力預緊緩沖器簡化模型
緩沖器在外界沖擊作用下質量塊m具有向下運動的趨勢,當沖擊力大于①和②磁鐵組的吸力和時,①和②NS極磁鐵分開,彈簧k開始壓縮變形,直至恢復平衡位置時,①和②磁鐵組恢復吸合;當質量塊從平衡位置開始向上運動時,此時向上沖擊力大于③和④組磁鐵的吸力,因此③和④的NS極開始分開,彈簧被拉伸,直至恢復平衡位置時,③和④組磁鐵分別重新吸合。每組兩個磁鐵之間存在相互吸引力Fm,Fm是關于磁鐵間距x的指數衰減函數。當兩個磁鐵之間的距離x達到最小時,Fm則達到一個最大值Fma,其就是磁力預緊緩沖器的初始預緊力。不論質量塊向上運動還是向下運動,當外界載荷力大于Fma時,對應的磁鐵組就會發生分離。隨著間距x增大,彈簧k開始發生變形并產生緩沖效果。當沖擊結束后,由彈簧的恢復力Fk將質量塊向上推動或向下拉,當間距x減小至一定值時,Fm指數增加,待質量塊恢復至平衡位置時,彈性力Fk不再對質量塊產生作用,在Fma的作用下,設備保持初始平衡位置狀態。
磁力預緊緩沖器的特點在于,當沖擊力在所設置的預緊力范圍之內時,其能夠保持剛性連接;當沖擊力超過該預緊力范圍時,為彈性元件支撐的彈性連接。與傳統預緊緩沖器所不同的是,傳統預緊緩沖器的彈性元件是產生預緊力的關鍵,兩者關系密切;而磁力預緊緩沖器的預緊力大小與彈性元件剛度無關,磁力預緊緩沖器可以在設定所需預緊力之后,根據需求設計彈性元件的剛度特性。磁力預緊緩沖器能通過選擇圓柱螺旋彈簧和強力磁鐵(NdFeB銣鐵硼磁鐵)進行組合設計。
根據圖1所示的工作原理,假設基礎沖擊激勵為z(t),設備響應為y(t),并且令x=y-z,那么受到基礎沖擊作用的磁力預緊緩沖器的運動微分方程如下
(1)
式中:M為設備質量;c為系統阻尼系數;k為系統彈性元件剛度;Fm為磁鐵間的相互作用力。
接下來對磁力預緊緩沖器的磁鐵元件特性、彈性元件特性進行研究,本文主要研究預緊力以及系統剛度對磁力預緊緩沖器沖擊響應的影響,暫不考慮阻尼作用。
1.2 磁鐵間的相互作用力
在磁力預緊緩沖器中,磁鐵之間的相互作用力是產生預緊力的關鍵,而且其剛度變化特性與傳統彈性元件存在區別。由于永磁鐵幾何形狀繁多,這里僅針對圓柱永磁鐵力學特性進行說明。為了簡化理論推導過程,這里做出四個假設條件:假設所用的圓柱永磁鐵都是使用相同的材質制作,具有相同的磁化強度矢量,具有相同的幾何尺寸并且關于圓柱體軸線對稱[9-10]。由于單對磁鐵所產生的力較小,因此所設計的磁力預緊緩沖器中具有多組磁鐵同時進行作用,如圖2(a)所示。將單對圓柱永磁鐵單獨拿出分析,其幾何參數標識如圖2(b)所示。

圖2 柱狀磁鐵空間分布
單對永磁鐵的靜磁能量的定義如下
(2)
式中:μ0為真空磁導率其值為4π×10-7H·m-1;H(r)為磁場強度;M(r)為磁化強度矢量。
永磁鐵之間的相互作用力可以通過對靜磁相互作用能量進行求導獲得。這里將坐標系統的z軸正向設置為圓柱永磁鐵的中心軸正向,那么沿著z軸方向的吸引力就能夠表達為
(3)
式中,Jd為偶極耦合積分,其表達式為
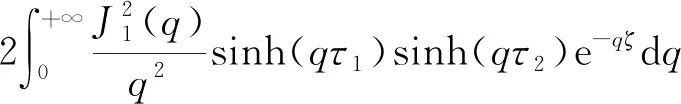
(4)
式中:τi=ti/(2R),其中i=1,2為兩個圓柱的幾何比例系數;ζ=Z/R為兩個柱狀磁鐵之間的有效距離;J1(q)為第一類修正貝塞爾函數。
在本文中所設計的磁力預緊緩沖器中,由于永磁鐵的幾何尺寸相同。因此τ1=τ2=τ,所以由式(4)和式(5)可得圓柱磁鐵之間的吸引力公式為
(5)
式(5)中,Kd=μ0M2/2為靜磁能量常數。Vokoun已經對公式的準確性進行了驗證,分別對單對磁鐵和2×2排列磁鐵之間的磁力-間隙關系進行了試驗,其中2×2排列磁鐵之間的磁力-間隙試驗曲線見圖3[11-12]。
在本文所設計的磁力預緊緩沖器中,所選定永磁鐵的幾何尺寸為,R=1.5 mm,t=1.5 mm。其排布方式同樣為2×2排列,因此對吸引力-位移特性與圖3所示曲線相同。

圖3 2×2排列圓柱永磁鐵的力-位移特性
為了進一步計算磁力預緊緩沖器的動態響應解,需要綜合考慮磁力預緊緩沖器中所有彈性元件的力-位移特性。而磁力預緊緩沖器中的彈性元件主要包括圓柱永磁鐵和線性彈簧。其中線性彈簧的力-位移特性可由下式表示
Fk=kx
(6)
式中,k為線性彈簧的剛度,單位為N/mm。
雖然,圓柱永磁鐵之間相互作用力可以利用式(5)表示,但為了簡化動態響應的計算過程,對式(5)進行簡化。而通過觀察圖3,發現圖中曲線具有衰減特性,因此這里采用指數衰減函數進行擬合,假設其擬合函數表達式如下
(7)
在擬合過程中,利用萊文貝格-馬夸特方法提供非線性最小化數值解。當n=1時,校正相關系數值為0.998,體現出較好的擬合度。因此圖3曲線的擬合函數可以表示為
y=Ae-x/μ1
(8)
式中,A和μ1為擬合系數,具體數值如表1所示。

表1 擬合參數
綜上所述,結合圓柱磁鐵力學特性和線性彈簧力學特性,磁力預緊緩沖器彈性元件的綜合力-位移特性可以表達為
Fz=Fk+Fm=kx+Ae-x/μ1
(9)
2 磁力預緊緩沖器緩沖性能
2.1 方程求解
利用諧波平衡法(harmonic balance method,HBM)對非線性系統方程求解。已知系統的綜合剛度特性,剛度特性中含有非線性函數項A1e-x/μ1,因此利用泰勒級數展開式來作為該函數項的近似表達。泰勒級數展開式如下所示
(10)
取n=3,則非線性函數項Ae-x/μ1的泰勒級數三階表達式為
(11)
因此,系統綜合剛度特性曲線可以通過下式表示
(12)
將式(12)代入方程式(1)中,當不考慮阻尼作用時,可以獲得以下運動微分方程
(13)
令,
因為只考慮系統的固有特性,因此令方程中的激勵項為零,則式(13)可表達為
(14)
設方程式(14)的解為
x=A0+A1coswt+A2cos 2wt
(15)
將式(15)代入方程式(14)中,并令方程的常數項cosφ和cos 2φ的系數相等。
(16)
(17)
(18)

(19)
(20)
于是可得方程式(14)的解為
(21)
其中,
(22)
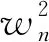
2.2 沖擊響應特性
磁力預緊緩沖器的沖擊響應特性是直接評估它自身緩沖性能的指標,接下來利用四階龍格庫塔對磁力預緊緩沖器的運動微分方程進行求解。而且為了較為全面地分析磁力預緊緩沖器的緩沖性能,分別研究了不同磁性預緊力、不同線性剛度對沖擊響應的影響。由于本文研究對象為艦船慣導設備,其所受到的沖擊載荷主要為水下非接觸爆炸對艦船所產生的正負雙波載荷[13]。因此利用正負雙波載荷對磁力預緊緩沖器的沖擊響應性能進行研究。為了能夠起到較好的緩沖作用,將緩沖器的緩沖頻率控制在20 Hz以內。這里所采用的沖擊載荷的正波和負波加速度幅值分別為50 g和10 g,脈寬分別為5 ms和25 ms。
磁性預緊力是磁力預緊緩沖器的關鍵特性,在此列舉四組不同的預緊力值,并計算不同預緊力對磁性預緊緩沖器的沖擊響應影響。為了進行合理的對比,這里將線性彈簧的剛度均設置為k1=40 Mg/L,其中M為設備質量(kg),g為重力加速度(m/s2),L為單位長度(m),其剛度取值,如表2所示。

表2 線性剛度參數
不同預緊力的磁力預緊緩沖器力-位移特性如圖4所示,圖4中系統所對應的相對位移響應、相對速度響應和加速度響應分別如圖5~圖7所示。圖5為磁力預緊緩沖器的位移響應規律,從圖中可以看出,不同預緊力對磁力預緊緩沖器的位移響應幾乎沒有影響。圖6為磁力預緊緩沖器的加速度響應規律,預緊力對加速度響應的局部響應峰值產生影響,預緊力越大,局部響應峰值越高,但是對總體響應影響并不大,這是因為局部響應峰值主要受到初始平衡位置磁力剛度影響,而總體響應峰值主要受線性剛度影響;另外,磁力預緊緩沖器的速度響應和加速度響應具有相同的規律,如圖7所示。

圖4 磁力預緊緩沖器力學特性(k1)

圖5 磁力預緊緩沖器位移響應(k1)
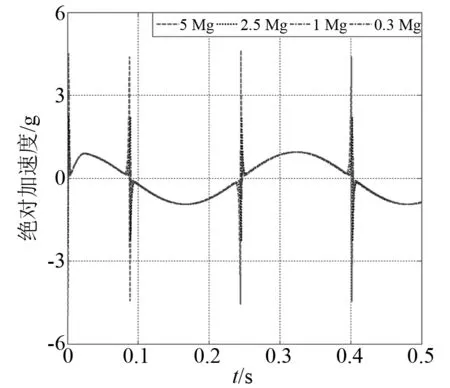
圖6 磁力預緊緩沖器加速度響應(k1)

圖7 磁力預緊緩沖器速度響應(k1)
在研究了磁性預緊力大小對緩沖器沖擊響應的影響后,接下來通過設置相同的磁性預緊力,來研究不同線性剛度對沖擊響應的影響。這里所考慮的線性剛度大小分為兩組,第一組在磁力預緊緩沖器極限位移處的恢復力值小于預緊力;第二組在磁力預緊緩沖器極限位移處的恢復力值大于預緊力。這里所提及的極限位移為沖擊載荷所產生的最大位移,其數值大小為23 mm。第一組工況中所涉及系統對應的線性剛度參數如表2所示,所對應數值計算結果分別如圖8~圖11所示。
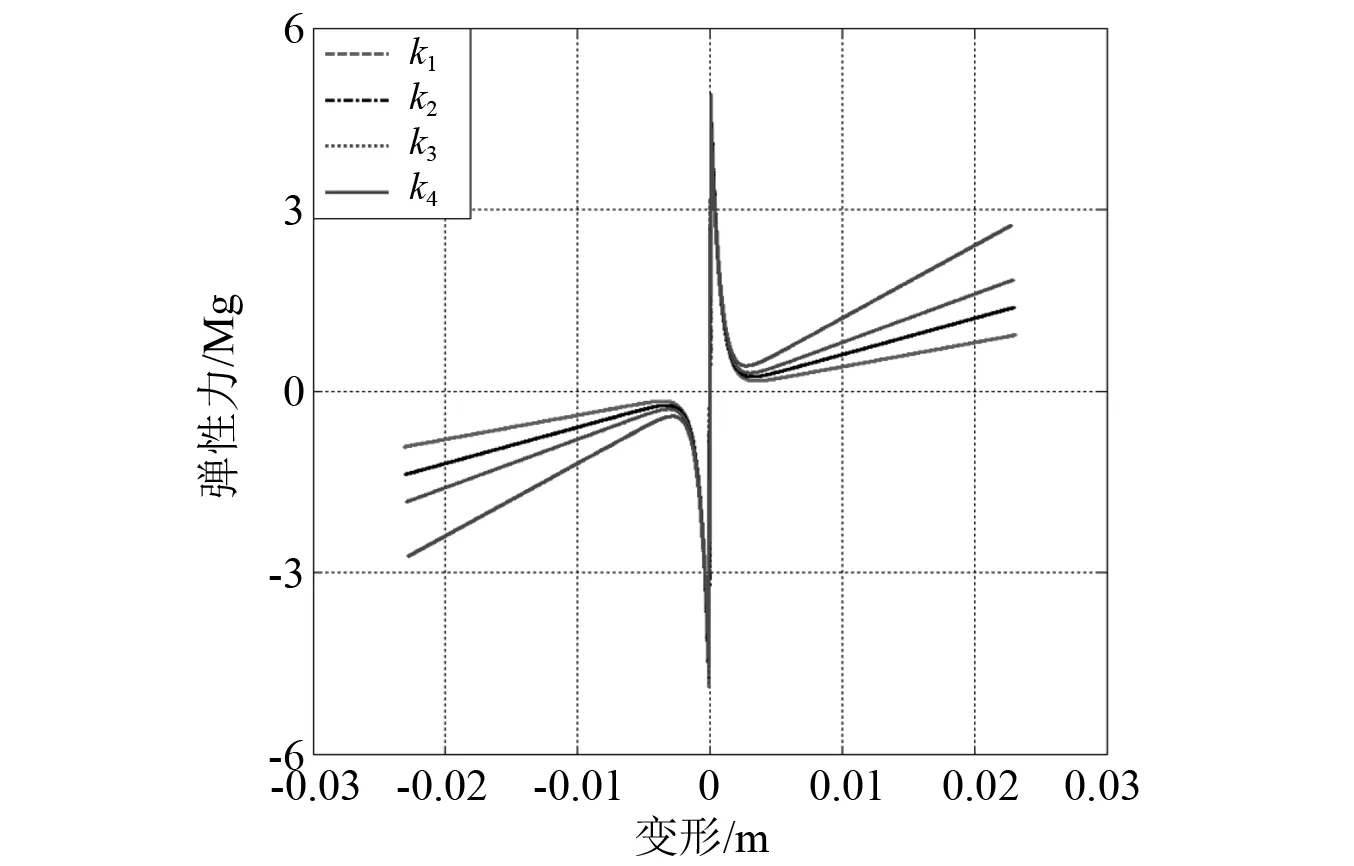
圖8 磁力預緊緩沖器力學特性(第一組工況)
通過觀察圖9~圖11,可以發現線性剛度對磁力預緊緩沖器沖擊響應周期影響較大,剛度越大則響應周期越小,這一規律與線性隔離系統相同。另外,通過觀察圖9發現,不同剛度的變化對位移響應幅值影響較小,基本保持在同一個水平。

圖9 磁力預緊緩沖器位移響應(第一組工況)

圖10 磁力預緊緩沖器加速度響應(第一組工況)

圖11 磁力預緊緩沖器速度響應(第一組工況)
除此之外,還分析了當磁力預緊緩沖器極限位移處的恢復力值大于預緊力時,線性剛度對沖擊響應的影響,即第二組工況。第二組工況所對應數值計算結果如圖12~圖15所示,從圖中可以觀察到系統響應周期依然與線性剛度值相關。
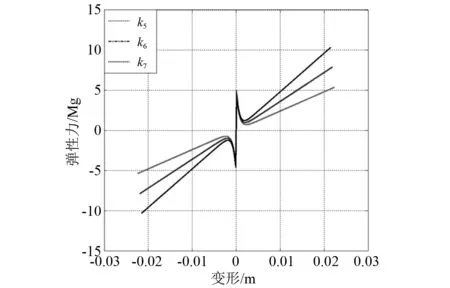
圖12 磁力預緊緩沖器力學特性(第二組工況)
通過觀察圖13中的位移響應,發現當線性剛度增加到較大值時,其位移響應幅值隨著線性剛度值增加而明顯減小。值得注意的是,磁力預緊緩沖器的加速度響應幅值超過了系統所設置的預緊力值大小,如圖14所示。因此如果要提高系統的緩沖性能,應該選擇合適的線性剛度值。從圖15可以看出,系統的速度響應幅值是隨著線性剛度增加而增加。
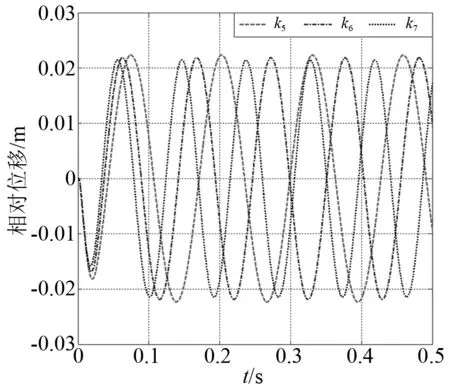
圖13 磁力預緊緩沖器位移響應(第二組工況)

圖14 磁力預緊緩沖器加速度響應(第二組工況)
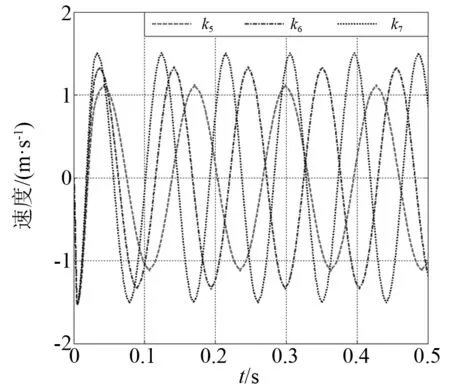
圖15 磁力預緊緩沖器速度響應(第二組工況)
3 不同種類緩沖器性能對比
在振動工程領域,經常用于沖擊載荷緩沖的沖擊緩沖器通常具有非線性特性,例如橡膠、空氣彈簧、鋼絲繩緩沖器以及含預緊力緩沖器。恒力緩沖器是一種理想狀態下的含預緊力緩沖器,能夠在已有的位移邊界條件下,能夠獲得最優的加速度響應解[12]。而一般的彈性元件的剛度都不為零,因此其所對應的預緊力緩沖器的加速度響應都是大于恒力緩沖器的響應。
由于本文所設計的緩沖器屬于含預緊力的非線性緩沖器范疇,因此在接下來的計算中,將其緩沖性能與線性預緊緩沖器、恒力預緊緩沖器進行對比。傳統的預緊緩沖器和磁力預緊緩沖器的的力-位移特性曲線分別如圖16(a)和圖16(b)所示。

圖16 含預緊力緩沖器力學特性
在圖16(a)中,F0表示傳統預緊緩沖器初始預緊力,Fc(x)為具有預壓縮量線性預緊緩沖器的力學特性,Fh(x)為恒力預緊緩沖器的力學特性,Fq(x)為準零剛度預緊緩沖器的力學特性;在圖16(b)中,Fm0為磁力預緊緩沖器的初始預緊力,Fm(x)為磁鐵元件的力學特性,F(x)為線性彈性元件的力學特性,而Fz(x)為磁力預緊緩沖器的力學特性,其為磁鐵元件和線性彈性元件力學特性的疊加。
從圖16(a)可以看出,當線性預緊緩沖器所受到大于初始預緊力的沖擊載荷之后,緩沖器就會產生變形,而且系統的響應力是在預緊力的基礎上逐漸增加。而準零剛度緩沖器或者恒力緩沖器,在外界力的作用下,其響應力基本是保持在一個小范圍內或者保持一定。而對于磁力預緊緩沖器而言,當外界載荷大于預緊力之后,永磁鐵力快速失去作用,沖擊就會直接作用在具有過零剛度特性的線性彈性元件上,相對應的沖擊響應力也可能會低于初始預緊力。
雖然磁力預緊緩沖器具有初始預緊力,都能夠保證系統在小干擾作用下保持穩定,但是其在功能結構上不同于傳統的預緊式緩沖器。當沖擊力大于預緊力時,磁力預緊緩沖器在平衡位置附近具有較小的沖擊力響應。因此在相同的剛度條件下,磁性預緊力緩沖器能夠保證加速度響應不大于傳統預緊緩沖器,甚至是恒力緩沖器。假設不同種類緩沖器性能的初始預緊力相同,均為5 Mg(M代表設備的質量)這個預緊力主要用于保證系統初始平衡位置的穩定性,從而能夠抵抗微小擾動。在此假設條件下,利用加速度響應幅值、速度響應幅值和位移響應幅值來評估不同種類緩沖器的優缺點。
3.1 不同緩沖器的沖擊響應
由于線性緩沖器不存在初始預緊力,其在沖擊作用下的響應主要受到沖擊載荷特性和系統固有頻率的影響,其位移、速度、加速度響應如圖17所示。從圖中可以看出,從2~10 Hz的頻率范圍內,位移響應幾乎相同,這是因為低頻段的單自由度系統位移響應幅值存在漸近值;而速度和加速度響應都是隨著頻率的增加而增大。

圖17 線性緩沖器的沖擊響應
張春輝研究了一種恒力緩沖器,該緩沖器在沖擊作用下的響應頻率受到預緊力大小和沖擊載荷幅值的影響。恒力緩沖器為傳統預緊緩沖器中的特例,在相同的位移響應情況下,其具有最優的加速度響應幅值,因此在這里將其作為對比對象之一,恒力緩沖器的力學特性曲線如圖18所示。

圖18 恒力緩沖器力學特性
不同恒力預緊緩沖器的沖擊響應如圖19~圖21所示。
可以發現在恒力緩沖器在相同沖擊載荷作用下,系統的響應頻率受到預緊力大小的影響,而且系統響應頻率隨著預緊力的增大而增大。
另外,從圖19和圖21可以看出,恒力預緊緩沖器的預緊力越大,就會導致加速度和速度響應幅值增大。從圖19可以看出,不同預緊力對位移響應幅值基本上沒有影響。這也就說明當載荷幅值與預緊力比值越小,系統的響應頻率就會增加。另外,通過觀察可以發現,所計算的恒力緩沖器沖擊響應的頻率都在10 Hz之內。
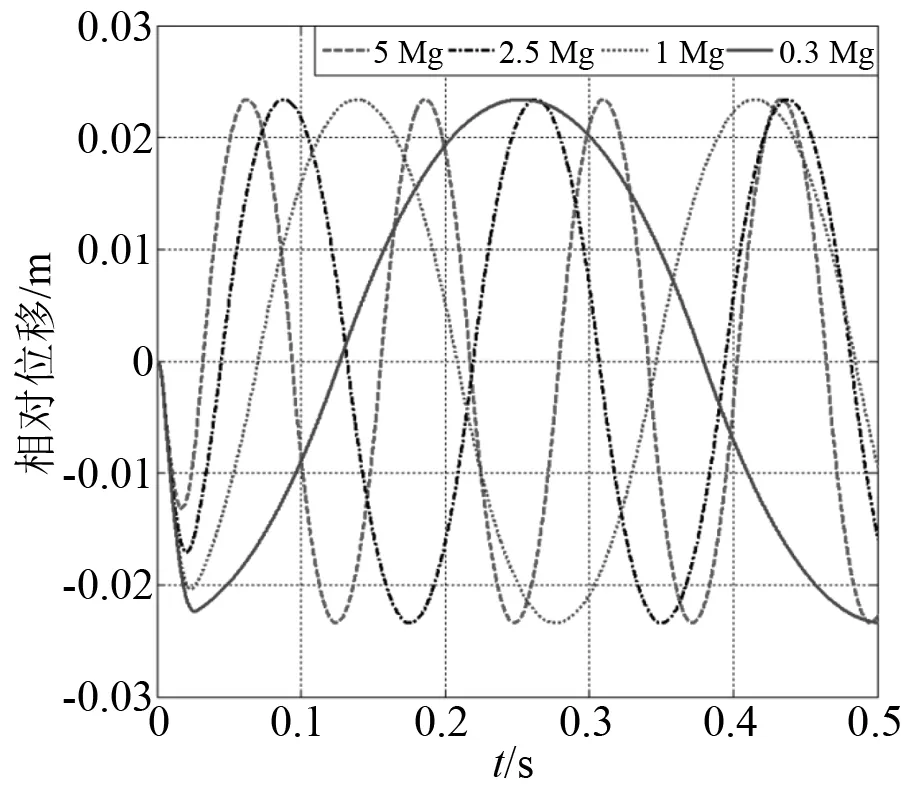
圖19 恒力緩沖器位移沖擊響應
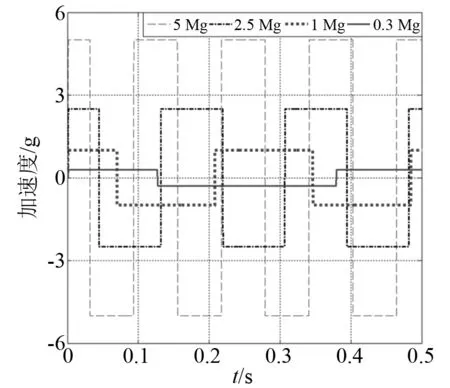
圖20 恒力緩沖器加速度沖擊響應

圖21 恒力緩沖器速度沖擊響應
從上述的響應結果可以看出,系頻率受到預緊力大小的影響。因為當緩沖距離確定時,預緊力增加會導致緩沖階段的有效剛度增大,從而導致在緩沖階段的固有頻率增加。而恒力緩沖器響應周期主要受到緩沖階段有效剛度的影響。除此之外,恒力緩沖器加速度響應幅值由所設定的預緊力所決定,而位移響應受到緩沖階段固有頻率、緩沖距離、預緊力大小的影響。通過位移響應的第一個峰值變化,發現預緊力增加導致位移響應明顯增加,但是該變化僅在第一個峰值表現明顯,在穩態響應中的變化不明顯。
接下來研究不同預緊力及剛度對線性預緊緩沖器沖擊響應的影響。線性預緊緩沖器的力學特性如圖22所示,其對應的沖擊響應規律分別如圖23~圖25所示。
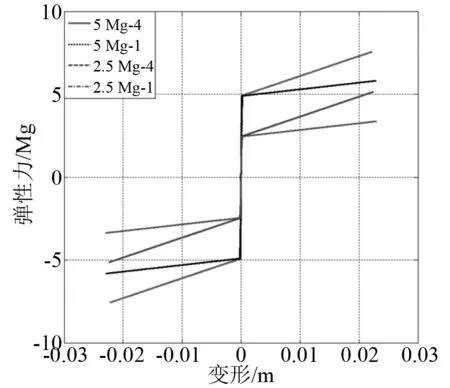
圖22 線性預緊緩沖器力學特性
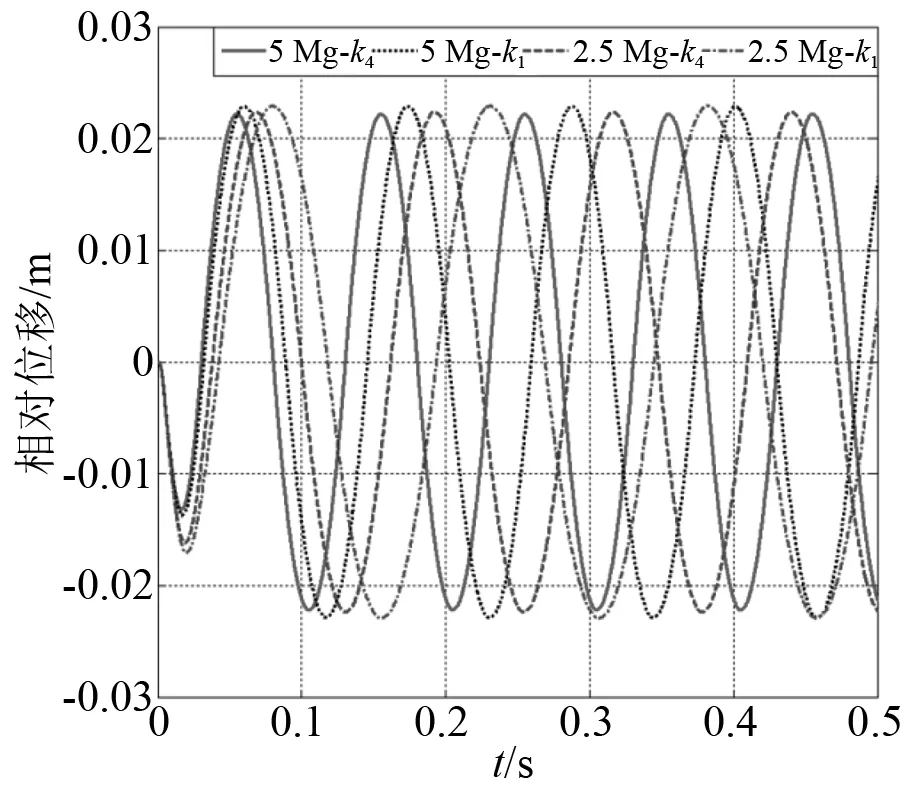
圖23 線性預緊緩沖器位移響應

圖24 線性預緊緩沖器加速度響應

圖25 線性預緊緩沖器速度響應
通過觀察可以發現,線性預緊緩沖器的響應周期受到預緊力和線性剛度值的影響。當線性剛度相同的情況下,所設置的預緊力越大其響應周期就越小;而當預緊力相同的情況下,所設置的線性剛度越大其響應周期就越小。從圖24中可以看出,緩沖器加速度響應幅值受到預緊力和線性剛度大小的影響,而且都是成正相關;從圖25中可以看出,緩沖器的速度響應規律與加速度相類似,而位移響應規律與加速度響應相反。
3.2 不同緩沖器緩沖性能分析
為了合理對比不同緩沖器沖擊隔離性能,這里在保證預緊力相同的情況下,對不同預緊緩沖器的沖擊隔離性能進行對比,所對比的緩沖器力學特性曲線如圖26所示。將相同預緊力作用下的不同類型的預緊緩沖器、線性緩沖器的沖擊響應進行對比,對比結果如圖27~圖29所示。
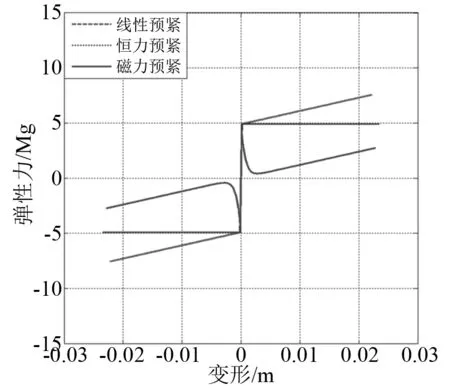
圖26 各類緩沖器力學特性對比
通過觀察圖27可以發現,恒力預緊裝置的位移響應與磁力預緊緩沖器的位移響應基本相同;通過觀察圖28可以發現,與線性隔離器相比,含預緊力緩沖器都能夠較好地降低系統的加速度響應,在傳統含預緊力緩沖器中恒力緩沖器具有最小的加速度響應,但是磁力預緊緩沖器的加速度響應還要小于恒力緩沖器;通過觀察圖29可以發現,磁力預緊緩沖器的穩態速度響應也是最小的,但是在沖擊過程中的速度響應是最大的。
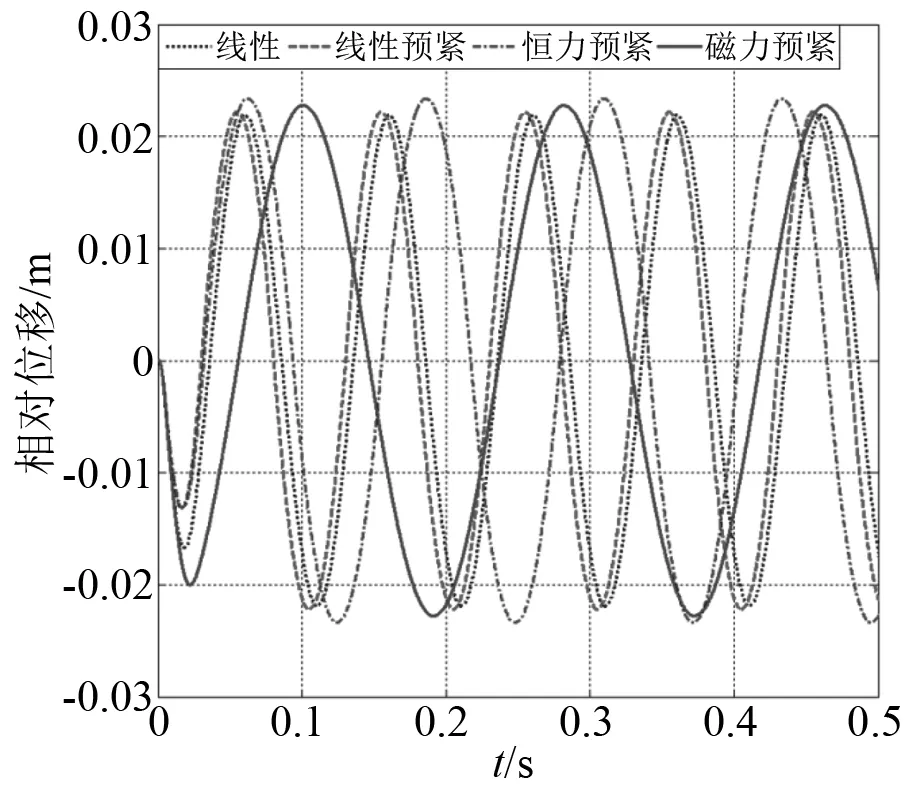
圖27 各類緩沖器位移響應對比

圖28 各類緩沖器加速度響應對比

圖29 各類緩沖器速度響應對比
從上述規律可以看出,磁力預緊緩沖器的預緊力對沖擊響應周期的影響不大。另外,從磁力預緊緩沖器的位移響應規律可以看出,其幅值大小與傳統預緊緩沖器和線性緩沖器的響應幅值相差很小;相比之下,磁力預緊緩沖器的速度響應幅值有所降低;加速度響應的有效面積有所降低。值得注意的是,在相同的預緊力下,磁力預緊裝置具有更長的響應周期,這是由于磁力預緊裝置的大變形響應階段具有負剛度和較低的線性剛度耦合作用,從而降低了系統的固有頻率。
為了對上述不同類型預緊力緩沖器性能進行對比分析,利用緩沖系數來評估緩沖器的性能。系統緩沖系數為評價沖擊隔離系統抗沖擊性能的綜合指標,其值越小表示系統的抗沖性能越好,系統緩沖系數的定義為
(23)
式中:amax為受保護設備的絕對加速度響應幅值;dmax為設備與基礎之間的相對位移響應幅值;v0為系統沖擊信號的階躍速度。接下來的將利用這個指標來作為不同預緊緩沖器的沖擊緩沖效果評估。根據上述計算結果中的最大位移響應、加速度響應以及沖擊載荷所對應的階躍速度(v0=1.559 5 m/s),從而計算不同緩沖器的緩沖系數大小,如表3所示。

表3 不同類型緩沖器緩沖系數
表3中,“磁力ki”表示磁力預緊緩沖器的全局緩沖系數,而“磁力kiv”表示有效緩沖系數,其中i=1,2,3,4。從表3可以看出,恒力預緊緩沖器與線性預緊緩沖器相比,具有較佳的緩沖表現。但是,與恒力預緊緩沖器相比,磁力預緊緩沖器具有更佳的緩沖性能。而磁力預緊緩沖器的全局緩沖效果隨著彈性元件剛度增加而表現更好的緩沖效果;但是有效緩沖系數隨著彈性元件剛度降低而表現更好的緩沖效果。
4 沖擊試驗
利用雙波沖擊試驗機對磁力預緊緩沖裝置進行沖擊試驗,對上述仿真結果進行驗證。通過兩種沖擊強度對不同剛度的磁力預緊裝置進行試驗。磁力預緊緩沖器原理樣機以及沖擊試驗原理分別如圖30所示。磁力預緊緩沖器質量塊重量為37 kg。

圖30 各類緩沖器加速度響應對比
利用雙波沖擊機產生兩種強度的沖擊載荷,所測試得到的加速度峰值分別為60 g和80 g。通過靜態拉伸試驗,測量得到2 Hz和6 Hz裝置的剛度分別為0.58 N/mm和5.15 N/mm。由靜態拉伸試驗測得單對永磁鐵所產生的最大吸引力為37 N,而在所設計的磁力預緊緩沖器中一種設置兩組永磁鐵,每組三對,則該裝置磁性預緊力為111 N。當系統剛度較低(2 Hz)時,磁力預緊結構就能夠實現較好的緩沖,兩次沖擊作用下系統加速度響應恒小于預緊力值大小,如圖31(a)和圖32(a);當沖擊載荷為60 g時,6 Hz裝置的沖擊加速度響應超過了預緊力值,如圖31(b)所示;當沖擊載荷為80 g時,6 Hz裝置的加速度響應進一步增大,如圖32(b)所示。上述沖擊試驗結果表明,當磁力緩沖器剛度較低時最大加速度響應不超過預緊力值,而隨著剛度增加以及沖擊強度的增加都會導致加速度響應超過預緊力值。這些現象說明沖擊試驗結果與2.2節中的理論計算結果一致,驗證了理論計算的準確性。
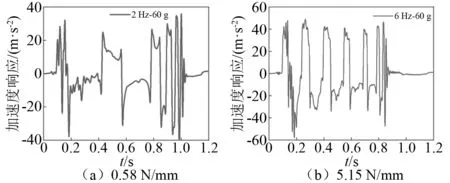
圖31 沖擊加速度響應(90 mm)
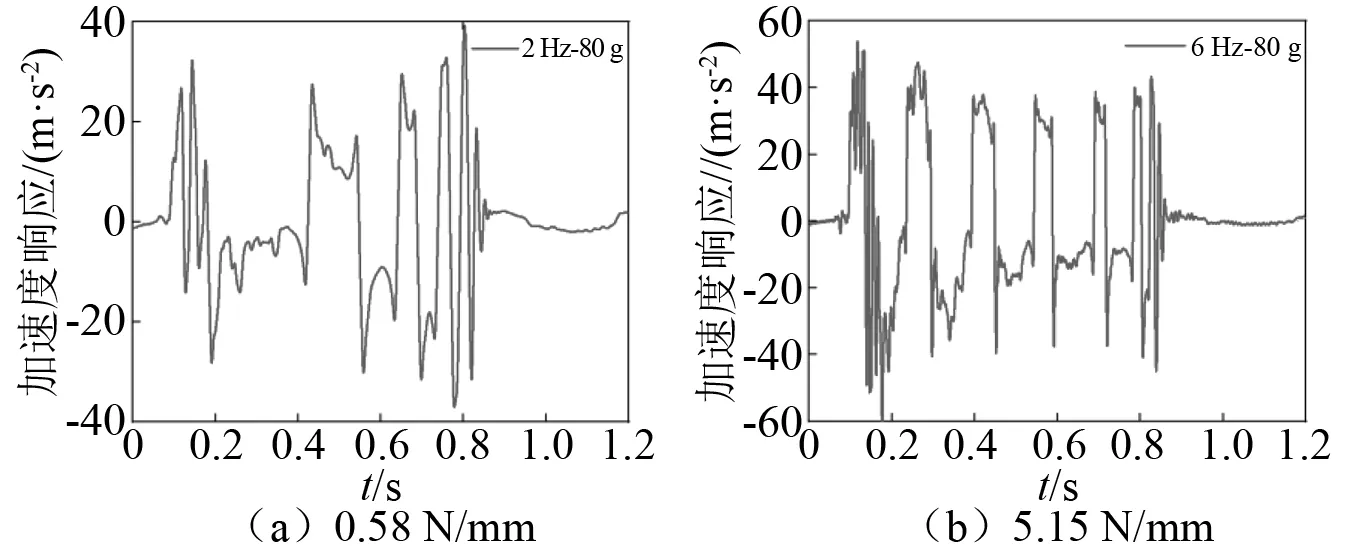
圖32 沖擊加速度響應(170 mm)
5 結 論
通過上述研究可以獲得以下結論:

(2) 磁力預緊裝置存在負剛度階段以及其特殊的負剛度特性,與傳統預緊力緩沖器相比具有更低的響應周期;由于這一特性,使得在相同預緊力下,磁力預緊緩沖器的加速度響應要小于恒力預緊緩沖器。
(3) 磁力預緊緩沖器的全局緩沖系數和有效緩沖系數都要低于傳統預緊緩沖器,具備較好的緩沖性能;而且若只考慮有效緩沖系數,其值甚至小于恒力緩沖器緩沖系數的25%,具有優秀的緩沖效果。而且雙波沖擊試驗結果與理論計算結果基本一致,驗證了理論計算的準確性。

